🧗 🐬 🛍️ n-Queens Completion Problem - algorithme de solution linéaire 🎏 🖤 🗺️

Ericgrig

Préface

Je voudrais commencer la préface par des remerciements à deux merveilleux programmeurs d'Odessa: Andrei Kiper (Lohica) et Timur Giorgadze (Luxoft), pour une vérification indépendante de mes résultats, au stade initial de l'étude.

L'article «Algorithme linéaire pour le problème d'achèvement de la solution n-Queens» a été publié dans (arXiv.org) au début du premier jour de 2020. Initialement, l'article était écrit en russe, donc la présentation de base est présentée ici, et il y a la traduction.
Cette tâche, et quelques-uns des nombreux ensembles NP-complets (la tâche de satisfaire les formules booléennes (3-SAT), la tâche de trouver la clique maximale, ou une clique d'une taille donnée ...) à différents moments, étaient dans mon domaine d'intérêt. Je cherchais une solution algorithmique basée sur diverses expériences de calcul, mais sans succès concret. C'était comme une personne essayant d'apprendre à se mettre en forme sur la barre horizontale d'un bras. Il n'y a pas de résultat, mais à chaque fois, il y a un espoir que tout se passera bientôt. La dernière fois, j'ai décidé que je devrais rester plus longtemps sur la tâche d'achèvement de n-Queens (en tant que membre de la famille) et essayer de faire quelque chose. Il convient de rappeler la merveilleuse blague d'Odessa: "Dans un bus bondé qui revient en banlieue sur une route cahoteuse le soir, la voix d'une femme se fait entendre - Mec, si tu m'as complètement couché dessus, alors fais au moins quelque chose."
L'étude a duré assez longtemps - près d'un an et demi. D'une part, cela est dû au fait que d'autres tâches ont été prises en compte dans le processus de recherche, et d'autre part, il y a eu des questions difficiles en cours de route, sans lesquelles nous ne pourrions pas avancer. J'en énumérerai quelques-uns:
- Il y a n lignes dans la matrice de décision, dans quel ordre l'index de ligne doit-il être sélectionné si le nombre de possibilités pour un tel choix est n!
- lorsqu'une ligne est créée, laquelle des positions libres restantes dans cette ligne doit être sélectionnée, car le nombre de possibilités pour une telle sélection est si grand qu'il peut être considéré comme un "proche parent" de l'infini (par exemple, le nombre de façons possibles de sélectionner une position libre dans toutes les lignes pour un échiquier de taille 100 x 100 est environ 10 ¹²⁴ )
- Ensemble, ces deux indicateurs forment un espace d'états (un espace de choix). Il semblerait qu'il y ait d'énormes opportunités, vous pouvez choisir ce que vous voulez. Mais derrière chaque choix spécifique à chaque étape, il y a un autre problème - la limitation du choix dans toutes les étapes suivantes. De plus, cela est particulièrement sensible dans les dernières étapes de la résolution du problème. On peut dire que la matrice de décision est "vindicative". Toutes les «erreurs inconscientes» que vous faites en faisant un choix aux étapes précédentes sont «accumulées», et à la fin de la décision, cela se manifeste dans le fait que dans les lignes où vous devez placer la reine, il n'y a pas de positions vides et la branche de recherche s'immobilise . Ici, comme avec Zhvanetsky: "un mauvais mouvement, et vous êtes enceinte."
- Lorsque la branche de la recherche d'une solution s'arrête, nous avons la possibilité de revenir à certaines des positions précédentes (Back Tracking), de sorte qu'à partir de cette position, nous recommencerons la formation de la branche de la recherche d'une solution. Il s'agit d'une «propriété» naturelle des problèmes non déterministes. La question est de savoir lequel des niveaux précédents doit être renvoyé. Il s'agit du même problème ouvert que la question du choix de l'index de ligne ou du choix d'une position libre dans cette ligne.
- Enfin, un problème lié à la vitesse de l'algorithme est à noter. Ce serait triste s'il n'y avait aucun objectif de créer des algorithmes rapides. Dans le processus de modélisation, il n'a pas été possible de développer un algorithme qui fonctionnerait rapidement et efficacement dans tous les domaines de la solution du problème. J'ai dû développer trois algorithmes. Ils transmettent les résultats les uns aux autres, comme un bâton. L'un d'eux fonctionne très rapidement, mais grossièrement, l'autre - au contraire, fonctionne lentement mais efficacement. Chacun travaille dans la «zone de sa responsabilité».
Initialement, le but de l'étude était seulement de trouver au moins une solution. J'avais beaucoup de choses à comprendre avant le développement de la première solution. Cela a pris plus de quatre mois. Il était possible de s'arrêter là, l'objectif était atteint - enfin, d'accord. Mais il me semblait que toutes les possibilités d'une solution algorithmique à ce problème n'étaient pas épuisées. Naturellement, il y avait un désir d'améliorer l'algorithme développé afin que la complexité temporelle de l'algorithme soit linéaire-O (n). Lorsqu'une telle solution linéaire a été trouvée, il y avait «un désir de plus» - de réduire le nombre de cas où la procédure Back Tracking (BT) a été utilisée dans la formation de la branche de recherche de solution. Il s'agissait d'un désir «impudent» de transférer la tâche du non déterministe au conditionnel (dans la mesure du possible). Cela a pris beaucoup de temps, mais l'objectif a été atteint, par exemple, dans l'intervalle de valeurs de la taille d'un échiquier n = (320, ..., 22500), le nombre de cas où la procédure BT n'a jamais été utilisée est supérieur à 50%. Il s'avère que dans 50% des cas lorsque le programme est lancé, l'algorithme forme «volontairement» une solution, jamais «trébuchant». (Rappelant le conte de fées sur le poisson rouge, je me suis arrêté sur ces deux envies ...)
En comparant les publications que j'ai pu connaître au cours de la recherche, je suis arrivé à la conclusion que ce problème et d'autres problèmes de ce type ne peuvent pas être résolus sur la base d'une approche mathématique rigoureuse, c'est-à-dire uniquement sur la base de définitions, d'énoncés de lemmes et de preuves de théorèmes. Il y a une «remarque philosophique» à ce sujet dans l'article. Je suis sûr que de nombreux problèmes des nombreux NP-Complete ne peuvent être résolus que sur la base des mathématiques algorithmiques avec l'utilisation de la modélisation informatique. Une telle conclusion ne signifie pas limiter les mathématiques, au contraire, cela signifie étendre les capacités des mathématiques par le développement de méthodes mathématiques algorithmiques. Pour chaque famille de problèmes, vous devez utiliser votre propre approche mathématique adéquate. (Pourquoi affecter un étudiant de troisième cycle à résoudre un problème de la famille NP-Complete sans appliquer de mathématiques algorithmiques et de méthodes de modélisation informatique, si l'on sait que rien ne viendra vraiment d'une telle entreprise).
Tout algorithme (programme) a une propriété simple - qu'il fonctionne ou non! Je veux lancer un appel aux membres de notre Habro-Community qui ont un ordinateur avec Matlab installé dans la zone d'accessibilité. Je veux vous demander de tester le fonctionnement de l'algorithme considéré pour résoudre le problème d'achèvement des n-reines . Cela ne prendra que 5 à 10 minutes. Pour tester l'algorithme, vous devez suivre quelques étapes simples:
- Générez une composition aléatoire à partir de k reines et vérifiez l'exactitude de cette composition.
- Sur la base de l'algorithme de décision proposé, complétez cette composition en une solution complète. Ou le programme doit décider que cette composition n'a pas de solution.
- Vérifiez l'exactitude de la solution obtenue à la suite de la configuration.
Vous n'avez pas besoin d'écrire de code pour de tels tests. En plus du programme principal, j'ai préparé deux autres programmes en langue Matlab:

1. Generarion_k_Queens_Composition - génération d'une composition aléatoire de taille k pour un échiquier arbitraire de taille nxn

2. Completion_k_Queens_Composition.m - compléter une composition arbitraire jusqu'à une décision complète, ou décider que cette composition n'a pas de solution ( programme principal ).

3. Validation_n_Queens_Solution.m - vérifier l'exactitude de la solution du problème des n-reines , ou l'exactitude de la composition de k reines.

Ils travaillent très vite. Par exemple, pour un échiquier d'une taille de 1000 x 1000 cellules, le temps total qu'il faut en moyenne pour générer une composition arbitraire (0,0015 s.), Complétez cette composition (0,0622 s.), Et vérifiez l'exactitude de la solution obtenue (0,0003 s.) ne dépasse pas 0,1 seconde. (à l'exclusion du temps nécessaire pour télécharger les données ou enregistrer les résultats)

Envoyez-moi un e-mail (ericgrig@gmail.com), si vous avez la possibilité d'aider un ami, je vous enverrai immédiatement ces trois programmes. Je serai reconnaissant à tous mes collègues qui peuvent tester objectivement l'algorithme et exprimer leur opinion dans la discussion.
J'ai préparé le code source du programme, avec des commentaires détaillés, qui, je l'espère, seront bientôt publiés sur Habré. Je pense que ceux qui sont intéressés à résoudre des problèmes complexes de la famille NP-Complete trouveront quelque chose d'intéressant pour eux-mêmes.
Je voudrais à nouveau lancer un appel aux membres de la communauté Habr, mais pour une raison différente. Ici, à Marseille (France), la formation de l'équipe France Fold Group est en cours, dont le but est de rechercher et développer des algorithmes de prédiction des propriétés physico-chimiques des composés de haut poids moléculaire. Je pense que cela ne vaut pas la peine de dire que c'est une tâche assez difficile, avec une longue histoire, et que des équipes sérieuses dans différents pays travaillent sur ce problème, y compris l'équipe Khasabis de Deep Mind (vous pouvez voir l'article sur Habré (habr.com_Folding) . L'objectif est de créer une équipe solide qui n'a pas peur de résoudre des problèmes complexes. La forme d'organisation de la collaboration est répartie. Chaque membre de l'équipe vit dans sa ville et travaille sur le projet pendant son temps libre de son travail principal. Nous avons besoin de programmeurs et de chercheurs (physiciens, chimistes, mathématiciens, biologistes) ), etc. osto "imprudents" programmers- (squared). Écrivez-moi si vous le trouvez intéressant, ce qui précède est mon e-mail. Plus en détail je peux le dire dans la lettre de réponse.

La préface de l'article s'est avérée être aussi longue que l'article lui-même. Le format de présentation familiale sur Habré me permet d'exprimer mes pensées plus librement, mais à en juger par la taille, j'en ai profité assez librement. Je voulais écrire brièvement, mais "cela s'est avéré comme toujours".

PS J'ai pensé que les membres de la communauté Habr seraient intéressés de savoir quelles difficultés j'ai rencontrées en essayant de publier les résultats de l'étude. Lorsque l'article a été préparé, je l'ai reformaté au format .tex selon les exigences du Journal of Artificial Intelligence Research (JAIR) et je l'ai envoyé là-bas. Il y avait des publications sur un sujet similaire. Il convient de noter en particulier l'article C. Gent, I.-P. Jefferson et P. Nightingale (2017) (Complexity of n-queens complètement) , dans lesquels les auteurs ont prouvé que le problème en question appartient à l'ensemble NP-Complete et ont évoqué les difficultés rencontrées pour tenter de résoudre ce problème. Dans les conclusions, les auteurs écrivent: «Pour toute personne qui comprend les règles des échecs, l'achèvement n-Queens peut être l'un des problèmes NP-Complete les plus naturels de tous» ( Pour tous ceux qui comprennent les règles des échecs, la tâche d'achèvement n-Queens peut devenir l'une des les tâches NP-Complete les plus naturelles ).

Au bout de 10 jours, j'ai reçu un refus de JAIR, avec la mention: «l'article ne correspond pas au format de la revue», c'est-à-dire n'a même pas pris l'article en considération. Je ne m'attendais pas à une telle réponse. Je pensais que si une revue publie des articles dans lesquels les auteurs concluent qu'il est très difficile de résoudre un problème donné et ne fournit aucune solution concrète, alors l'article qui fournit un algorithme de solution efficace sera certainement accepté pour examen. Cependant, les éditeurs avaient leur propre opinion sur cette question. (Je crois que des spécialistes compétents y travaillent, et très probablement ils ont été interrogés par le titre de l'article «impudent» et tout ce qui y est indiqué. Nous avons pensé: «il y a très probablement une sorte d'erreur et je me suis gentiment renvoyé, en référence au format ").

J'ai dû choisir une autre publication scientifique périodique évaluée par des pairs sur des sujets pertinents. Ici, je suis confronté à une dure réalité. Le fait est qu'environ 80% de tous les magazines sont payés: soit je dois payer un montant décent au magazine pour que l'article soit librement accessible à tous les lecteurs, soit ils doivent donner l'article en cadeau «à l'arc», et ils factureront tous ceux qui souhaite se familiariser avec cette étude. Et les première et deuxième options sont fondamentalement inacceptables pour moi. Je me sentais bien dans cette méthode de raquette d'éditeur lorsque j'ai essayé de me familiariser avec certaines publications.

Le prochain magazine, qui professe le principe du libre accès à l'information, était le SMAI Journal of Computational Mathematics . Ils ont également refusé avec le même libellé, bien que beaucoup plus rapidement - en deux jours.

Puis une revue a été choisie: Mathématiques discrètes et informatique théorique . Ici, les exigences sont simples, vous devez d'abord publier l'article dans arXiv.org, et seulement après cela, enregistrer l'article pour examen. D'accord, nous suivrons les règles - j'ai soumis un article dans arXiv.org . Ils m'ont écrit qu'ils publieraient l'article dans 8 heures. Cependant, cela ne s'est pas produit après 8 heures, pas après 8 jours. L'article a été «détenu» par les mentors, et ce n'est qu'après 9 jours qu'il a été publié. Aucune plainte n'a été formulée quant à la forme et à l'essence de l'article. Je pense que, comme dans le cas de JAIR, les mentors avaient des doutes quant à la possibilité de "faire ceci et d'écrire à ce sujet". Quelque temps plus tard, après avoir corrigé des erreurs techniques, l'article a été mis à jour et publié sous sa forme définitive le soir du Nouvel An.

Je dois m'y attarder en détail pour montrer qu'au stade de la publication des résultats de la recherche, il peut y avoir des problèmes qui ne peuvent pas être expliqués logiquement.

Ce qui suit est un article dont la traduction en anglais a été publiée sur (arXiv.org) .

1. Introduction

Parmi les différentes options pour formuler le problème des n-reines, la tâche d' achèvement des n-reines en question a une position particulière en raison de sa complexité. Dans leur travail (Gent at all (2017)) a montré que le problème de complétion n-Queens appartient à l'ensemble NP-Complete (a montré que n-Queens Completion est à la fois NP-Complete et # P-Complete ). Il est supposé que la solution à ce problème pourrait nous ouvrir la voie pour résoudre d'autres problèmes à partir de l'ensemble de NP-Complete .

Le problème est formulé comme suit. Il existe une composition de k reines, qui sont régulièrement réparties sur un échiquier de taille nxn . Il est nécessaire de prouver que cette composition peut être complétée en une solution complète, et de donner au moins une solution, ou de prouver qu'une telle solution n'existe pas. Ici, par cohérence, nous entendons une composition de k reines pour lesquelles trois conditions du problème sont remplies: dans chaque ligne, chaque colonne, ainsi que sur les diagonales gauche et droite passant par la cellule où se trouve la reine, pas plus d'une reine n'est localisée. Le problème sous cette forme a été formulé pour la première fois par Nauk (1850) .

1.1 Définitions

Ci-après, nous désignerons la taille du côté de l'échiquier par le symbole n . Une solution sera dite complète si toutes les n reines sont placées de manière cohérente sur un échiquier. Toutes les autres solutions, lorsque le nombre k de reines correctement placées est inférieur à n - nous appellerons la composition. Nous appelons une composition de k reines positive si elle peut être complétée avant une solution complète. En conséquence, une composition qui ne peut pas être complétée jusqu'à ce qu'une solution complète soit appelée négative. Comme analogue d'un «échiquier» de taille nxn , nous considérerons également une «matrice de solution» de taille nxn . A titre d'exemple, tous les algorithmes développés pour résoudre le problème seront présentés en langage Matlab.

L'étude a été réalisée sur la base d'une simulation informatique (simulation informatique). Pour tester telle ou telle hypothèse, nous avons effectué des expériences de calcul dans une large gamme de valeurs n = (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10000, 30 000, 50 000, 80 000, 10 ⁵ , 3 * 10 ⁵ , 5 * 10 ⁵ , 10 ⁶ , 3 * 10 ⁶ , 5 * 10 ⁶ , 10 ⁷ , 3 * 10 ⁷ , 5 * 10 ⁷ , 8 * 10 ⁷ , 10 ⁸ ) et, selon la valeur de n , des échantillons suffisamment grands ont été générés pour l'analyse. Nous appelons une telle liste une « liste de base de n valeurs » pour mener des expériences de calcul. Tous les calculs ont été effectués sur un ordinateur ordinaire. Au moment de l'assemblage (début 2013), c'était une configuration assez réussie: CPU - Intel Core i7-3820, 3,60 GH, RAM-32,0 Go, GPU-NVIDIA Ge Forse GTX 550 Ti, Périphérique disque - ATA Intel SSD, SCSI, OS- Système d'exploitation 64 bits Windows 7 Professionnel . Nous appelons ce kit simplement - desktop-13 .

2. Préparation des données

L'algorithme commence par lire un fichier qui contient un tableau unidimensionnel de données sur la distribution d'une composition arbitraire de k reines. On suppose que les données sont préparées de la manière suivante. Soit un tableau mis à zéro Q (i) = 0, i = (1, ..., n) , où les indices des cellules de ce tableau correspondent aux indices de ligne de la matrice de solution. Si dans une rangée arbitraire i de la matrice de solution il y a une reine en position j , alors l'affectation Q (i) = j est effectuée. Ainsi, la taille de composition k , sera égale au nombre de cellules non nulles du réseau Q. (Par exemple, Q = (0, 0, 5, 0, 4, 0, 0, 3, 0, 0) signifie que nous considérons une composition de k = 3 reines sur la matrice n = 10 , où les reines sont situées dans le 3e, 5e et 8e lignes, respectivement dans les positions: 5, 4, 3).

3. Algorithme pour vérifier l'exactitude du problème solution n-Queens

Pour la recherche, nous avons besoin d'un algorithme qui nous permettrait de déterminer l'exactitude de la solution du problème des n-reines en peu de temps. Le contrôle de l'emplacement des reines dans chaque ligne et chaque colonne est simple. La question concerne les limites diagonales. Nous pourrions construire un algorithme efficace pour une telle comptabilité si nous pouvions mapper chaque cellule de la matrice de solution à une certaine cellule d'un certain vecteur de contrôle qui caractériserait de manière unique l'influence des restrictions diagonales sur la cellule en question. Ensuite, selon que la cellule du vecteur de contrôle est libre ou occupée, on peut juger si la cellule correspondante de la matrice de décision est libre ou fermée. Une telle idée a été utilisée pour la première fois par Sosic & Gu (1990) pour prendre en compte et accumuler le nombre de situations conflictuelles entre différentes positions de reines.Nous utilisons une idée similaire dans l'algorithme présenté ci-dessous, mais uniquement pour prendre en compte si la cellule de la matrice de solution est libre ou occupée. La figure 1, à titre d'exemple, montre un échiquier 8 x 8 au-dessus duquel se trouve une séquence de 24 cellules.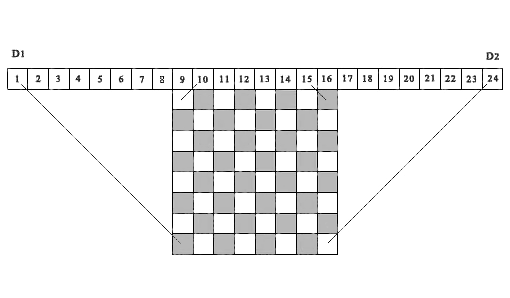

Fig.1. Un exemple de démonstration de la correspondance des projections diagonales des cellules de la matrice avec les cellules correspondantes des tableaux de contrôle D1 et D2 , ( n = 8)

Considérez les 15 premières cellules comme des éléments du vecteur de contrôle D1 . Les projections de toutes les diagonales gauches de n'importe quelle cellule de la matrice de solution tombent dans l'une des cellules du vecteur témoin D1 . En fait, toutes ces projections sont situées à l'intérieur de deux segments de ligne parallèles, dont l'un relie la cellule de matrice (8.1) à la première cellule du vecteur D1 , et le second relie la cellule de matrice (1.8) à la 15e cellule du vecteur de contrôle D1. Nous donnons une définition similaire pour les projections diagonales droites. Pour ce faire, déplacez la référence de la cellule 1 vers la cellule 9 vers la droite et considérez une séquence de 16 cellules comme des éléments du vecteur de contrôle D2 (dans la figure, ce sont des cellules du 9 au 24). Projections de toutes les diagonales droites de n'importe quelle cellule de la matrice les solutions tomberont dans l'une des cellules de ce vecteur de contrôle, à partir de la 2ème cellule à la 16ème (sur la figure, du 10 au 24). Ici, toutes ces projections sont situées entre deux segments de lignes parallèles - le segment reliant la cellule (8,8) de la matrice de solution à la cellule 16 du vecteur D2 (cellule 24 sur la figure) et le segment reliant la cellule (1,1) de la matrice de solution à la cellule 2 vecteurs de contrôle D2(cellule 10 sur la figure). Les projections de toutes les cellules de la matrice de solution se trouvant sur la même diagonale gauche tombent respectivement dans la même cellule du vecteur de contrôle gauche D1 , les projections de toutes les cellules de la matrice de solution se trouvant sur la même diagonale droite tombent dans le même cellule du vecteur de contrôle droit D2 . Ainsi, ces deux vecteurs de contrôle D1 et D2 , permettent un contrôle total de toutes les inhibitions diagonales pour n'importe quelle cellule de la matrice de décision.

Il est important de noter que l'idée d'utiliser des projections diagonales sur des cellules de vecteurs de contrôle pour déterminer si une cellule d'une matrice de solution avec les coordonnées (i, j) est libre ou occupée a également été implémentée plus tard dansRichards (1997) . Il fournit l'un des algorithmes de recherche récursive les plus rapides pour toutes les solutions, basé sur des opérations avec un masque de bits. Une différence importante est que l'algorithme indiqué est conçu pour la recherche séquentielle de toutes les solutions, à partir de la première ligne de la matrice de solution - vers le bas, ou de la dernière ligne de la matrice - vers le haut. L'algorithme que nous proposons est basé sur la condition que le choix du numéro de chaque ligne pour l'emplacement de la reine soit arbitraire. Pour l'algorithme considéré, cela est d'une importance fondamentale. Notez que la figure 1 ci-dessus, nous avons construit par analogie avec ce qui est publié dans cet article.
Un programme pour vérifier si une solution donnée du problème des n-reines est correcte, ou si une composition donnée de k est vraieQueens est le suivant.

1. Pour contrôler les inhibitions diagonales, créez deux tableaux D1 (1: n2) et D2 (1: n2) , où n2 = 2 * n, et un tableau B (1: n) pour contrôler l'occupation des colonnes de la matrice de solution. Remettez à zéro ces trois tableaux.

2. Nous introduisons le compteur du nombre de reines correctement installées ( totPos = 0 ). De manière cohérente, dans un cycle, à partir de la première ligne, nous considérons toutes les positions de reines fournies. Si Q (i)> 0 , alors sur la base de l'indice de la ligne i et de l'indice de la position de la reine dans cette ligne j = Q (i), nous formons les indices correspondants pour les tableaux de contrôle D1 (r) et D2 (t) :
r = n + j - i
t = j + i

3. Si toutes les conditions ( D1 (r) = 0, D2 (t) = 0, B (j) = 0 ) sont remplies , cela signifie que la cellule ( i, j) est libre et ne tombe pas dans la zone de projection des restrictions diagonales formées par les reines précédemment établies. La position de la reine dans cette position est correcte. Si au moins une de ces conditions n'est pas remplie, le choix d'une telle position sera respectivement erroné et la décision sera erronée.

4. Si la solution est correcte, incrémentez le compteur du nombre de reines correctement installées ( totPos = totPos + 1 ) et fermez les cellules correspondantes des tableaux de contrôle: (D1 (r) = 1, D2 (t) = 1, B (j) = 1) . Nous fermons donc toutes les cellules de la colonne(j) et les cellules de la matrice de solution qui sont situées le long des diagonales gauche et droite se croisant dans la cellule (i, j) .

5. Répétez la procédure de vérification pour toutes les positions restantes.
C'est peut-être l'un des algorithmes les plus rapides pour évaluer l'exactitude de la solution au problème des n-reines . Le temps de vérification d'un million de positions pour la matrice de solutions 10 ⁶ x 10 ⁶ sur desktop-13 est de 0,175 seconde, ce qui correspond approximativement au temps de pression sur la touche "Entrée". Évidemment, cet algorithme est linéaire par rapport au temps de comptage par rapport à n .

4. Description de l'algorithme de résolution du problème

Le général . Le problème d'achèvement des n-reines est un problème non déterministe classique. La principale difficulté de sa solution est liée à la question du choix de l'indice de ligne et de l'indice de position dans cette ligne, dans des conditions où l'espace d'état est énorme. Lors de la recherche de toutes les solutions possibles, un tel problème ne se pose pas. Nous devons considérer toutes les branches de recherche valides dans l'espace d'état, et l'ordre dans lequel elles sont considérées n'a pas d'importance. Cependant, lorsqu'une composition arbitraire de k reines doit être complétée jusqu'à une solution complète, alors dans ce cas, nous avons besoin d'un algorithme pour sélectionner les indices de ligne et de colonne qui perçoit correctement la composition existante et conduit à une solution plus rapidement que les autres. Dans ce projet, nous avons décidé la question du choix sur la base de la position générale suivante - si nous ne pouvons pas formuler des conditions qui donnent la préférence à n'importe quelle ligne ou n'importe quelle position de cette ligne par rapport aux autres, alors nous utilisons un algorithme de sélection aléatoire basé sur nombres aléatoires uniformément répartis . Une méthode de sélection aléatoire similaire pour résoudre des problèmes dans lesquels l'espace d'état est immense est tout à fait naturelle. L'une des éditions de la série Actes d'un atelier DIMACS (1999) a été entièrement consacrée à l'utilisation de la sélection aléatoire dans le développement d'algorithmes pour résoudre des problèmes complexes. La mise en œuvre correcte de l'algorithme de sélection aléatoire peut être une solution assez productive, bien que ce soit une condition nécessaire mais pas suffisante pour l'achèvement de la solution. Sosic et Gu (1990) est l'une des premières études à utiliser un algorithme de sélection aléatoire pour résoudre le problème des n-reines . L'algorithme qu'ils ont examiné est basé sur une idée assez simple et concise. Soit une suite de nombres de 1 à n , qui sont réarrangés aléatoirement. Un tel ensemble de nombres a une propriété importante. Cela consiste dans le fait que peu importe la façon dont ces nombres sont répartis sur différentes lignes de la matrice de solution comme les positions de la reine (un nombre par ligne), les deux premières règles seront toujours remplies dans l'énoncé du problème: chaque ligne et chaque colonne n'auront pas plus d'une reine. Cependant, seule une partie des positions ainsi obtenues sera exempte de restrictions diagonales. L'autre partie sera en «conflit» avec les reines établies précédemment. Pour sortir de cette situation, les auteurs ont utilisé la méthode de comparaison et d'échange de positions conflictuelles afin d'obtenir une solution complète. Dans notre algorithme proposé, les situations de conflit sont impossibles, car à chaque étape de résolution du problème, la reine n'est installée dans la cellule de la ligne en question que si la cellule est libre.

4.1 Sélection d'un modèle pour le suivi arrière (BT)

Dans le processus de recherche d'une solution à un problème, une situation peut survenir lorsqu'une chaîne séquentielle de solutions mène à une impasse. Il s'agit d'une propriété «génétique» des problèmes non déterministes. Dans ce cas, vous devez revenir à l'une des étapes précédentes, restaurer l'état de la tâche conformément à ce niveau et recommencer la recherche d'une solution à partir de cette position. La question est de savoir lequel des niveaux précédents doit être renvoyé et combien de ces niveaux doivent être (par niveau, nous entendons une certaine étape dans la résolution du problème avec un nombre donné de reines correctement installées). De toute évidence, le choix d'un niveau de solution pour revenir en arrière est tout aussi pertinent que le choix d'un indice de ligne ou d'un indice de position dans cette ligne. Par conséquent, quelle que soit l'approche de résolution de ce problème, il est nécessaire de déterminer d'abord le nombre de niveaux de base pour revenir en arrière, ainsi que le mécanisme et les conditions pour revenir à l'un de ces niveaux. Dans notre algorithme proposé, nous divisons la matrice de solution en trois niveaux de base. Ce sont les points de retour. Si, à la suite de la solution, un blocage se produit, alors, selon les paramètres de la tâche, nous revenons à l'un de ces trois niveaux de base. Le premier niveau de base ( baseLevel1 ) correspond à l'état lorsque la vérification des données de la composition en question est terminée. C'est le début du programme. Les valeurs des deux niveaux de base suivants ( baseLevel2 et baseLevel3 ) dépendent de la taille de la matrice n . La dépendance empirique de ces valeurs de base à la taille de la matrice de solution a été établie sur la base d'un grand nombre d'expériences de calcul. Pour une représentation plus précise de cette dépendance, nous avons divisé tout l'intervalle considéré de 7 à 10 ⁸ en deux parties. Soit u = log (n) , alors si n <30 000 , alors

baseLevel2 = n - rond (12.749568 * u3 - 46.535838 * u2 + 120.011829 * u - 89.600272)
baseLevel3 = n - rond (9.717958 * u3 - 46.144187 * u2 + 101.296409 * u - 50.669273)

sinon

baseLevel2 = n - round (-0.886344 * u3 + 56.136743 * u2 + 146.486415 * u + 227.967782)
baseLevel3 = n - rond (14.959815 * u3 - 253.661725 * u2 + 1584.713376 * u - 3060.691342)

4.2 Structure des blocs

L'algorithme est construit sous la forme d'une séquence de cinq blocs d'événements , où chaque événement est associé à l'exécution d'une certaine partie de la solution au problème. Les algorithmes de traitement de chaque bloc sont différents les uns des autres. Seuls trois des cinq blocs servent à former une chaîne séquentielle de solutions, et les deux autres blocs sont préparatoires. Le choix du numéro de bloc à partir duquel les calculs commencent dépend de la valeur de n et des résultats de la comparaison de la taille de composition k avec les valeurs de baseLeve2 et baseLevel3 . Une exception est l'intervalle de valeurs n = (7, ..., 99) , qui peut être appelé une «zone turbulente» en raison des particularités du comportement de l'algorithme dans cette section. Pour les valeurs n = (7, ..., 49) , quelle que soit la taille de la composition, après saisie et suivi des données, les calculs commencent à partir du 4ème bloc. Pour les valeurs n = (50, ..., 99) , selon la taille de la composition, les calculs commencent soit à partir du deuxième bloc, soit à partir du quatrième. Comme mentionné ci-dessus, à chaque étape de la résolution du problème, seules les positions dans la ligne sont prises en compte qui ne tombent pas dans la zone de restrictions créée par les reines précédemment établies. Ce sont ces positions que l' on appelle libres .
Décrivons brièvement quels calculs sont effectués dans chacun de ces cinq blocs du programme.

4.3 Début de l'algorithme

Les données sont entrées et la composition est vérifiée pour l'exactitude. A chaque étape de vérification, les cellules des matrices de contrôle sont modifiées. Le nombre de reines correctement installées est compté. S'il n'y a aucune erreur dans la composition, la solution continue, sinon un message d'erreur s'affiche. Une fois la vérification terminée, des copies des tableaux principaux sont créées pour leur réutilisation à ce niveau. Après cela, le contrôle est transféré au bloc-1 .

4.4 Bloc 1

Le début de la formation de la branche de recherche. Nous considérons k reines situées sur un échiquier comme une position de départ. Il est nécessaire de continuer à compléter cette composition et de placer les reines sur un échiquier jusqu'à ce que leur nombre total soit égal à baseLevel2 . L'algorithme utilisé ici est appelé randSet & randSet . Cela est dû au fait que nous comparons ici constamment deux listes d'indices aléatoires, à la recherche de paires exemptes des restrictions diagonales correspondantes. Pour ce faire, les actions suivantes sont effectuées:

a) deux listes sont formées: une liste des indices de lignes libres et une liste des indices de colonnes libres;

b) réarrangement aléatoire des nombres dans chacune de ces listes;

c) dans une boucle, chaque paire de valeurs successives (i, j) , où l'indice (i) est sélectionné dans la liste des indices de lignes libres et l'index (j) dans la liste des indices de colonnes libres, est considérée comme une position reine potentielle et il est vérifié si cela position dans la zone de projection des exceptions diagonales.

Si la règle des exceptions diagonales n'est pas violée, la position est considérée comme correcte et la reine est placée dans cette position. Après cela, le compteur est incrémenté pour le nombre de reines correctement installées et les cellules correspondantes des matrices de contrôle sont modifiées. Si la position (i, j) tombe dans la zone de restrictions diagonales formée par les reines établies précédemment, alors rien ne change et la transition vers la considération de la prochaine paire de valeurs a lieu.

Lorsque le cycle de comparaison de toutes les paires de la liste est terminé, puis, sur la base des indices restants qui se trouvent dans la zone d'exclusion diagonale, une liste des indices des lignes et colonnes libres restantes est à nouveau formée, et cette procédure est répétée jusqu'à ce que le nombre total de reines correctement placées (totPos ) ne sera pas égal ou supérieur à la valeur limite de baseLevel2 . Une fois cette condition remplie, le contrôle est transféré au bloc 2 . S'il s'avère qu'à la suite d'une recherche de solution, une situation est survenue que dans la liste complète des index des lignes et colonnes libres restantes, aucune des paires ne convient à l'emplacement de la reine, alors dans ce cas, les valeurs d'origine des tableaux de contrôle sont restaurées sur la base des copies générées précédemment et le contrôle est transféré au début du bloc 1 pour un nouveau comptage.

4.5 Bloc 2

Ce bloc sert de phase préparatoire à la transition vers le bloc 3 . À ce niveau, le nombre de lignes libres restantes ( freeRows ) est nettement inférieur à n . Cela vous permet de transférer des événements de la matrice d'origine de taille nxn vers une matrice de plus petite taille L (1: freeRows, 1: freeRows) . De plus, sur la base d'informations sur les lignes et colonnes libres restantes dans la matrice de solution d'origine, des zéros sont écrits dans les cellules correspondantes du tableau L , indiquant que ces cellules sont libres. Avec cette transition de "projection" , la correspondance des indices de ligne et de colonne de la nouvelle matrice avec les indices correspondants de la matrice d'origine est préservée. Il est important de noter que bien que, dans le processus de résolution de ce problème, tous les événements se déroulent sur la matrice initiale de taille nxn , et qu'une telle matrice soit l'arène principale de l'action, en réalité une telle matrice n'est pas créée , et ne contrôle que les tableaux de comptabilité pour les indices de ligne A (1: n) et colonnes B (1: n) de cette matrice.

Avec le tableau L, deux tableaux de travail rAr (1: freeRows) et tAr (1: freeRows) sont également formés dans ce bloc pour enregistrer les indices correspondants des tableaux de contrôle D1 et D2 . Cela est dû au fait que lorsque nous installons la reine suivante dans la cellule (i, j) de la matrice initiale de taille nxn , nous devons ensuite exclure les cellules du tableau L qui tombent dans la zone de projection des exceptions diagonales du tableau "grand" d'origine. Étant donné que le contrôle des contraintes diagonales est effectué uniquement dans la matrice d'origine de taille nxn , la présence de tableaux de travail rAr et tAr nous permet de maintenir la correspondance et de traduire les cellules interdites aux limites du tableau L. Cela simplifie considérablement la comptabilisation des positions exclues.
Une fois les travaux préparatoires terminés dans ce bloc, des copies des tableaux principaux sont créées pour être réutilisées à ce niveau et le contrôle est transféré au bloc 3 .

4.6 Bloc 3

Dans ce bloc, la formation de la branche de recherche de solution se poursuit sur la base des données préparées dans le bloc précédent. Le nombre de lignes dans lesquelles les reines sont correctement définies est égal ou supérieur à baseLevel-2 . Vous devez continuer à sélectionner jusqu'à ce que le nombre de reines installées soit égal à baseLevel-3 . Ici, nous utilisons l'algorithme de recherche de solution rand & rand , c'est-à-dire pour former la position d'une reine, au lieu d'une liste d'index libres, seuls deux index sont utilisés, une valeur d'index aléatoire d'une ligne libre et une valeur d'index aléatoire d'une position libre dans cette ligne. Cette procédure est répétée cycliquement jusqu'à ce que le nombre total de reines placées soit égal à la valeur de baseLevel-3 . Dès que cette condition est remplie, le contrôle est transféré au bloc 4 . Si, à la suite de calculs, la branche de recherche s'avère être une impasse, alors cette section de la formation de la branche de recherche est fermée et elle revient au début du bloc 3 , d'où les calculs sont répétés. Pour cela, les valeurs initiales de tous les tableaux de contrôle sont restaurées.

4.7 Bloc 4

Dans ce bloc, les données sont préparées pour le transfert de contrôle au bloc 5 . À cette étape, après avoir terminé la procédure du bloc 3 , le nombre de lignes libres ( nRow ) est devenu encore moins. Par conséquent, il est également avantageux de traduire les événements d'un tableau plus grand en un tableau plus petit. Cette approche nous donne l'occasion de déterminer rapidement les caractéristiques nécessaires pour les lignes restantes dont nous avons besoin à ce stade. D'une importance particulière est le fait que sur la base d'un tel tableau, il est possible de prédire les perspectives de la branche de recherche pour de nombreux pas en avant sans avoir à terminer les calculs. La condition est assez simple. S'il s'avère que parmi les lignes libres restantes, il existe une ligne dans laquelle il n'y a pas de position libre, alors la branche de recherche considérée est fermée et le contrôle est transféré vers l'un des blocs de niveau inférieur. Les actions préparatoires menées ici sont largement similaires à ce qui a été fait dans le bloc 2 . Sur la base des indices d'origine des lignes et des colonnes libres, un nouveau tableau bidimensionnel est formé, dont les valeurs nulles correspondent aux positions libres dans la matrice de solution d'origine. De plus, un tableau spécial E (1: nRow, 1: nRow) est créé dans ce bloc, sur la base duquel vous pouvez déterminer le nombre de positions libres dans les lignes libres restantes qui seront fermées si vous sélectionnez la position (i, j) pour définir la reine dans matrice source. Avant de transférer le contrôle au bloc 5 , les actions suivantes sont effectuées:

a) le nombre de postes vacants dans toutes les lignes restantes est déterminé,

b) un tableau de la quantité de positions libres, pour les lignes en question, est trié par ordre croissant,

c) si toutes les lignes libres restantes ont des positions libres (c'est-à-dire que la valeur minimale dans cette liste classée est différente de 0), alors le contrôle est transféré au bloc 5.

S'il s'avère que dans aucune des lignes restantes il n'y a de position libre, les tableaux nécessaires sont restaurés en fonction des copies stockées et, selon les paramètres de la tâche, le contrôle est transféré à l'un des niveaux de base.

d) des copies de sauvegarde de toutes les baies de contrôle pour ce 4ème niveau sont formées.

4.8 Bloc 5

Cette étape est définitive, et ici, la formation de la branche de recherche s'effectue de manière plus «équilibrée» et «rationnelle». C'est le "dernier kilomètre", il ne reste qu'un petit nombre de lignes libres. Mais en même temps, c'est la partie la plus difficile. Toutes les erreurs qui auraient pu être commises aux étapes précédentes de la formation de la branche de la recherche d'une solution, dans l'ensemble, apparaissent ici - sous la forme d'un manque de position libre dans la ligne.

L'algorithme de ce bloc est exécuté sur la base de deux boucles imbriquées, à l'intérieur desquelles la troisième boucle est exécutée. Une caractéristique du troisième cycle est qu'il peut être répété, sans changer les paramètres de deux cycles externes. Cela se produit si la branche de recherche générée est bloquée. Le nombre de ces répétitions ne dépasse pas la valeur limite de repeatBound , dont la valeur optimale a été établie sur la base d'expériences de calcul.

L'indice de boucle externe est associé à un choix séquentiel d'indices de ligne qui sont restés libres après les calculs au troisième niveau de base. Cela se fait sur la base d'une liste de lignes précédemment classée par le nombre de positions libres dans la ligne. La sélection commence par une ligne, avec un nombre minimum de positions libres, puis, dans les étapes suivantes, par ordre croissant. A l'intérieur de ce cycle, un deuxième cycle se forme, dont l'indice réitère les indices de toutes les positions libres de la ligne considérée. Le premier cycle n'a pour but que de sélectionner l'indice de l'une des lignes libres à ce niveau. En conséquence, le but du deuxième cycle est seulement de sélectionner une position libre dans la ligne considérée. Ces actions se produisent uniquement au troisième niveau de base. Après ce choix, le nombre de reines installées est incrémenté et les cellules correspondantes de toutes les baies de contrôle sont modifiées. De plus, le contrôle est transféré à l'intérieur d'un (troisième) cycle imbriqué, dont la zone d'activité est déjà constituée de toutes les lignes libres restantes. A l'intérieur de ce cycle, le choix de l'index de ligne et le choix d'une position libre dans cette ligne sont effectués selon les règles suivantes:

a) Sélectionnez une ligne gratuite . Toutes les lignes libres restantes sont prises en compte et le nombre de positions libres est déterminé sur chaque ligne. La ligne est sélectionnée pour laquelle le nombre de positions libres est minimal. Cela minimise les risques liés à la possibilité d'exclure les derniers postes vacants dans certaines des lignes restantes dans lesquelles l'État est minimal et critique en termes de nombre de postes vacants ( règle du risque minimum ). Par ailleurs, c'est avec cette règle à l'esprit que l'index du premier cycle de ce cinquième bloc commence par une sélection séquentielle de lignes avec une valeur minimale du nombre de positions libres dans une ligne. Si à un moment donné, il s'avère que les deux lignes ont le même nombre minimum de positions libres, alors l'index de l'une des deux positions répertoriées en premier dans la liste classée est sélectionné au hasard. Si le nombre de lignes ayant le même nombre minimum de positions libres est supérieur à deux, alors l'indice de l'une des trois positions répertoriées en premier dans la liste classée est sélectionné au hasard.

b) Sélection d'une position libre d'affilée .Dans la liste de tous les postes vacants dans la ligne en question, un est sélectionné qui cause un minimum de dommages aux postes vacants dans toutes les lignes restantes. Cela se fait sur la base du tableau précédemment formé E. Par «dommages minimaux», nous entendons le choix d'une telle position dans une ligne donnée qui exclut le moins de positions libres dans toutes les lignes restantes ( règle des dommages minimaux) S'il s'avère que deux ou plusieurs positions libres consécutives ont les mêmes valeurs minimales selon le critère de dommage, alors l'indice de l'une des deux positions répertoriées en premier dans la liste est sélectionné au hasard. Le choix d'une position qui exclut le nombre minimum de positions libres dans les lignes restantes minimise les «dégâts» associés à la position de la reine dans cette position. L'utilisation de ces deux règles permet une utilisation plus rationnelle des ressources à chaque étape de la formation d'une branche de recherche. Cela réduit considérablement les risques et augmente la probabilité de choisir une composition arbitraire pour une solution complète si la composition en question a une solution. Si, à un certain stade de la solution, il s'avère que dans l'une des lignes restantes à examiner, il n'y a pas de postes vacants, cette branche de recherche est fermée. Dans ce cas,en fonction des sauvegardes, toutes les baies de contrôle sont restaurées et si le nombre de répétitions ne dépasse pas la valeur limiterepeatBound, puis sans changer les indices des premier et deuxième cycles externes, le travail du troisième cycle imbriqué se répète. Cela est dû au fait que dans les cas où les valeurs minimales des critères pertinents coïncidaient, nous avons effectué une sélection aléatoire. La reconstitution de la branche de recherche dans les mêmes conditions du niveau de base permet une utilisation plus efficace des «ressources de départ» fournies à ce niveau. Le nombre de démarrages répétés du troisième cycle imbriqué est limité et si la valeur limite est dépassée, le fonctionnement de ce cycle est interrompu. Après cela, les valeurs des matrices de contrôle sont restaurées et le contrôle est transféré au cycle du troisième niveau de base pour passer à la valeur d'index suivante. Cette procédure est répétée cycliquement jusqu'à ce qu'une solution complète soit obtenue, ou il s'avère queque nous avons utilisé toutes les lignes libres et toutes les positions libres dans ces lignes à ce niveau de base. Dans ce cas, en fonction du nombre total de calculs répétés à différents niveaux de base, et en tenant compte de la taille de la matrice de décision et de la taille de la composition, on revient à l'un des niveaux inférieurs pour les calculs répétés, ou l'on juge que la composition en question ne peut pas être équipé pour compléter la solution. Dans le programme, afin de limiter la durée totale de la facture, il est admis que la procédureou un jugement est rendu que la composition en question ne peut être achevée avant une décision complète. Dans le programme, afin de limiter la durée totale de la facture, il est admis que la procédureou un jugement est rendu que la composition en question ne peut être achevée avant une décision complète. Dans le programme, afin de limiter la durée totale de la facture, il est admis queLe suivi arrière , quel que soit le niveau précédent auquel le retour est effectué, ne peut pas être effectué plus de fois totSimBound . Cette valeur limite est sélectionnée sur la base d'expériences de calcul pour diverses valeurs de n.

5. Analyse de l'efficacité des algorithmes de sélection

L'efficacité de l' algorithme randSet & randSet . Pour analyser les capacités de cet algorithme, une expérience de calcul a été réalisée, qui a consisté à placer des reines dans la matrice de solution basée sur le modèle randSet & randSet tant que cette possibilité existe. Dès que la branche de recherche a atteint une impasse ou qu'une solution complète a été obtenue, la taille de la composition, le temps de solution ont été fixés et le test a été répété à nouveau. Des expériences de calcul ont été effectuées pour toute la liste de base de n valeurs . Le nombre de tests répétés pour les valeurs n = (30, 40, ..., 90, 100, 200, 300, 500, 800, 1000) était égal à un million , pour les valeurs restantes, le nombre de tests, avec l'augmentation de nPeu à peu diminué , passant de 100 000 à 100. L'analyse des résultats des expériences de calcul vous permet de faire les conclusions suivantes:

a) En raison de seulement le premier cycle de la procédure randSet et randSet en moyenne sont correctement espacées d' environ 60% de toutes les reines. Pour n = 100, le nombre de reines correctement placées est de 60,05%. Avec une augmentation de la valeur de n, cette valeur diminue progressivement, et pour n = 10 ^{7 elle} s'élève à 59,97%.

b) L'histogramme de la distribution des valeurs de longueur des compositions obtenues a la même forme, quelle que soit la taille de la matrice de décision n. De plus, ils ont tous une caractéristique - le côté gauche de la distribution (à la valeur modale) diffère du côté droit. La figure 2, à titre d'exemple, montre l'histogramme correspondant pour

Fig.2. Un histogramme de la distribution des solutions de différentes longueurs pour le modèle randSet & randSet ( n = 100, taille de l'échantillon = 10 ⁶ ).

n = 100. Il semble que l'histogramme soit collecté à partir de la distribution de fréquence de deux événements différents, car la fréquence d'occurrence des événements dans les parties gauche et droite de la distribution est différente. Pour décrire cette distribution, il est très probablement approprié d'utiliser deux fonctions de la densité de la distribution normale, dont l'une couvre l'intervalle jusqu'à la valeur modale, l'autre - l'intervalle après la valeur modale.

c) La valeur moyenne du nombre de reines ( qMean ) qui peuvent être définies dans la matrice de décision basée sur cet algorithme augmente avec n. Comme le montre la figure 3, où un graphique de la dépendance du rapport qMean / n à la taille de matrice n est présenté , ce rapport augmente avec une augmentation de la taille de matrice. Par exemple

Fig.3. La dépendance du rapport qMean / n à la valeur de n pour différentes tailles de la matrice de solution. Le modèle est randSet & randSet , qMean est la valeur moyenne de la longueur de la solution.

si pour une matrice 100x100 l' algorithme de sélection de position randSet & randSet permet "sans s'arrêter" de placer des reines en moyenne 89 lignes, alors pour une matrice 1000x1000 , le nombre de ces lignes augmente en moyenne à 967.

d) Sur la base de l' algorithme randSet & randSet, vous pouvez obtenir la pleine une solution, cependant, la «productivité» de cette approche est extrêmement faible. Comme le montre la figure 4, pour

Fig.4. La diminution de la probabilité d'obtenir une solution complète dans le modèle randSet & randSet avec une augmentation de n .

valeurs de n = 7, la probabilité d'obtenir une solution complète est de 0,057 . De plus, avec une augmentation de n, la probabilité d'obtenir une solution complète diminue rapidement, se rapprochant asymptotiquement de zéro. A partir de la valeur n = 48, la probabilité d'obtenir une solution complète est de l'ordre de 10 ^-6 . Après la valeur seuil n = 70, pour les valeurs suivantes de n, aucune solution complète n'a été obtenue (avec le nombre de tests égal à un million ).

e) ModèlerandSet & randSet forme des branches de recherche à très grande vitesse. Pour n = 1000, le temps moyen d'obtention de la composition est de 0,0015 seconde. La longueur moyenne des compositions est de 967. Par conséquent, pour n = 10 ^{6, le} temps moyen est de 2,6754 secondes avec une longueur moyenne des compositions de 999793.

f) À l'exception d'un petit intervalle n <= 70, lorsque le modèle randSet & randSet dans de très rares cas peut conduire à solution complète, dans tous les autres cas, la branche de décision se termine par la formation d'une composition négative, qui ne peut être complétée qu'après une solution complète. Donc, l' algorithme randSet & randSetIl présente un avantage important - la grande vitesse de formation de la branche de recherche, et un inconvénient important est que si la taille de la composition dépasse une certaine valeur de seuil, cet algorithme conduit à la formation de compositions qui ne peuvent être achevées qu'après une solution complète. Pour pallier cet inconvénient, on arrête la formation de la branche de recherche lorsque le seuil baseLevel-2 est atteint .

L'efficacité de l'algorithme rand & rand . Pour déterminer les capacités de l'algorithme rand & rand , une simulation informatique assez détaillée a été effectuée pour une liste de base de n valeurs . Comme avec le modèle randSet & randSet, le nombre de nouveaux tests dans la plupart des cas était égal à un million . Pour les autres valeurs, le nombre de tests est progressivement passé de 100 000 à 100.

Les deux algorithmes sont basés sur le principe de la sélection aléatoire. Par conséquent, il faut s'attendre à ce que les conclusions tirées ici soient fondamentalement identiques aux conclusions formulées pour le modèle randSet & randSet . Cependant, il existe une différence fondamentale entre eux, et elle consiste en ce qui suit:

a) le modèle rand & rand ne fonctionne pas aussi "dur" que le modèle randSet & randSet . Si nous parlons d'un «indice d'utilisation rationnelle des opportunités offertes», le modèle rand & randà chaque étape, utilise les ressources de manière plus rationnelle. Cela conduit au fait que, par exemple, à n = 30, la probabilité d'obtenir une solution complète de 0,00170 dans ce modèle est 15 fois supérieure à la valeur similaire de 0,00011 pour le modèle randSet & randSet . De plus, ici, jusqu'à la valeur seuil n = 370, la probabilité d'obtenir au moins une solution complète pendant un million de tests demeure. Après cette valeur seuil, pour des valeurs ultérieures de n avec un nombre de tests égal à un million, aucune solution complète n'a été obtenue sur la base du modèle rand & rand .

b) cet algorithme est beaucoup plus lent que l' algorithme randSet & randSet . Si pourn = 1000 pour générer une composition de taille 967, le temps moyen pour obtenir une composition sera de 0,0497 secondes, soit 33 de plus que la valeur correspondante de 0,0015 pour le modèle randSet & randSet .

La raison des différences entre deux méthodes de sélection aléatoire essentiellement similaires est due au fait que dans le modèle randSet & randSet , afin d'accélérer les calculs, la sélection aléatoire dans la liste restante n'est pas effectuée à chaque étape. Au lieu de cela, une paire d'indices est sélectionnée séquentiellement à partir de deux listes, dont les éléments ont été réarrangés au hasard. Une telle sélection n'est pas complètement aléatoire, cependant, elle correspond bien à la logique du problème et vous permet de compter rapidement.

Démonstration visuelle du fonctionnement de l'algorithme rand & rand, l'expérience suivante a été réalisée:

a) Pour un échiquier de taille 100x100, après chaque étape de l'emplacement de la reine sur une ligne, le nombre de positions libres dans chacune des lignes libres restantes a été déterminé. Ainsi, après chaque étape de résolution du problème, nous avons reçu une liste de lignes libres et une liste correspondante du nombre de positions libres dans ces lignes. Cela a permis de construire un graphe où les indices des colonnes de la matrice en question sont tracés le long de l'axe des abscisses, et le nombre de positions libres restantes le long de l'axe des ordonnées. A titre de comparaison, les calculs ont également été effectués pour le modèle de sélection séquentielle des positions. Par sélection séquentielle, on entend ce qui suit. La première ligne est considérée, dans laquelle la première position libre dans la liste est sélectionnée. Ensuite, la deuxième ligne est considérée, dans laquelle la première position libre dans la liste, etc. est également sélectionnée. Aux figures 5 et 6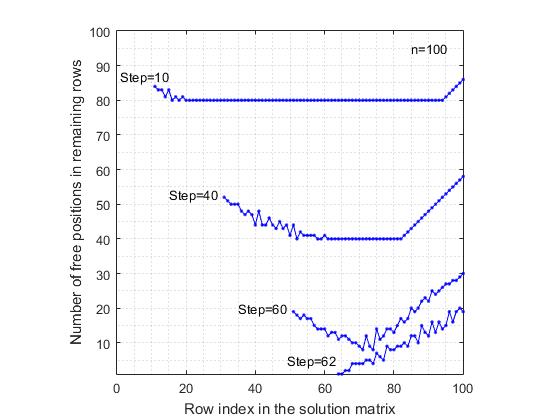

Fig.5. Réduction du nombre de positions libres dans les lignes libres restantes après le placement des reines. Sélection séquentielle régulière de postes.

Les résultats correspondant aux modèles considérés sont présentés. Pour plus de clarté, le graphique montre les résultats uniquement après les étapes (10, 40, 60). Pour le modèle de sélection séquentielle de positions, le dernier est le graphique après la 62e étape, car la branche de recherche se termine en raison de l'absence d'une position libre dans la 63e ligne. En revanche, dans le modèle rand & rand , le dernier graphique est présenté après la 70ème étape de placement de la reine, bien qu'ici, le nombre moyen de reines correctement placées atteigne 89, soit 26 pas de plus que dans le modèle séquentiel. Une vue étrange des graphiques du modèle rand & randen raison du fait que l'index de ligne est sélectionné au hasard parmi les lignes libres restantes, et donc elles sont dispersées au hasard dans la matrice de la solution. Une comparaison de ces deux figures montre que dans le modèle séquentiel de sélection de position, la plage de variabilité du nombre de positions libres est plus élevée que dans le modèle rand & rand . Cela est dû au fait qu'avec une sélection régulière, les contraintes diagonales excluent de manière non uniforme les positions libres dans les lignes restantes, ce qui conduit au fait que dans certaines lignes, le taux de réduction du nombre de postes vacants est plus élevé que dans d'autres lignes.

Fig.6. Réduction du nombre de positions libres dans les lignes libres restantes après le placement des reines. Le modèle de positionnement est rand & rand .

En revanche, avec la sélection aléatoire de l'indice de ligne libre et de l'indice de colonne libre, les positions de la reine sont réparties uniformément sur la "zone" de la matrice de décision, ce qui réduit le taux de réduction "moyen" du nombre de positions libres dans les lignes restantes. Ainsi, en tenant compte des capacités de l'algorithme rand & rand , nous l'utilisons dans le programme pour continuer la formation de la branche de recherche de solution jusqu'à ce que le niveau baseLevel-3 soit atteint .

Il est à noter que même si les algorithmes de sélection ( randSet & randSet, rand & rand) ne serait pas aussi efficace, il nous faudrait encore utiliser une autre méthode de sélection aléatoire lors du développement de l'algorithme. Cela est dû à l'énoncé même du problème d'achèvement des n-reines . Si nous imaginons qu'il existe un certain algorithme optimal qui résout le problème, alors à l'entrée, un tel algorithme recevra toujours un certain ensemble aléatoire d'indices de ligne et de colonne. Chaque fois, ce sera un nouvel ensemble aléatoire d'indices de lignes et de colonnes à partir d'une grande variété de possibilités. Afin de pouvoir «absorber» l'algorithme d'une telle variété de compositions aléatoires, l'algorithme lui-même doit être construit sur la base d'une sélection aléatoire. La correspondance devrait être comme une clé pour la serrure . Si nous construisons l'algorithme sur ce principe, alors toute composition cohérente dek reines seront considérées comme la position initiale (de départ) dans le cycle de recherche de décision. Et de plus, le but ne sera que de continuer la formation de la branche de la recherche d'une solution jusqu'à ce qu'une solution soit trouvée pour une composition donnée, ou qu'il soit prouvé qu'une telle solution n'existe pas.

6. Un exemple d'utilisation de la règle du risque minimum (n = 100)

Au stade initial de la recherche d'une solution, lorsque le nombre de positions libres dans les lignes n'est pas critique, le choix de l'index de la ligne libre ou de l'index de la position dans cette ligne n'est pas fatal. Cependant, à la dernière étape, lorsque le nombre de positions libres dans certaines lignes est de 1 ou 2, dans ce cas, vous devez choisir un algorithme de sélection différent. À ce niveau, les algorithmes de sélection aléatoire randSet & randSet et rand & rand ne fonctionneront plus.

La raison pour laquelle les algorithmes de sélection aléatoire ne fonctionneront pas peut être expliquée par l'exemple simple suivant. Soit à une étape de la résolution du problème, pour une valeur arbitraire de n, dans les lignes restantes i ₁ , i ₂ , ..., i _kle nombre de postes vacants (indiqués entre parenthèses) est: i ₁ (1), i ₂ (2), i ₃ (4), i ₄ (5), i ₅ (3), i ₆ (4) , etc. Si nous sélectionnons au hasard une ligne, mais pas la ligne i ₁ , dans laquelle il n'y a qu'une seule position libre, cela peut conduire à une situation à risque lorsque les interdictions diagonales liées à la position de la reine dans la ligne sélectionnée peuvent entraîner la fermeture de la seule position libre dans la ligne i ₁ , ce qui entraînera l'arrêt de la solution. De toutes les lignes i ₁ , i ₂ , ..., i _kla plus vulnérable et la plus sensible au choix de l'index de ligne est la ligne i ₁ . Dans de telles situations, vous devez d'abord sélectionner la ligne dont l'état est le plus critique et crée un risque pour résoudre le problème. Par conséquent, à la dernière étape de la résolution du problème, à chaque étape, il est nécessaire de choisir la position de la ligne sur la base d'un algorithme simple de risque minimal.

Pour plus de clarté, considérons, à titre d'exemple, pour une matrice 100 x 100 , la dernière étape de la formation d'une solution réelle, après la 88e étape. Jusqu'à la fin de la tâche, il restait 12 lignes libres, pour chacune desquelles le nombre de positions libres a été trouvé (les lignes sont classées par ordre croissant du nombre de positions libres):Étape 89 - 25 (1), 12 (2), 22 (2), 82 (2), 88 (2), 7 (3), 64 (3), 3 (4), 76 (4), 91 (4), 4 (5), 96 (5) - indique l'index d'une ligne libre, et entre parenthèses - le nombre de positions libres sur cette ligne. Selon la règle du risque minimum, à la 89e étape de résolution du problème, la ligne 25 est sélectionnée et cette position libre qui s'y trouve. À la suite du recomptage, il nous reste 11 lignes libres: Étape 90 - 7 (2), 12 (2), 22 (2), 82 (2), 88 (2), 3 (3), 64 (3), 76 (3), 4 (4), 91 (4), 96 (4).Comme vous pouvez le voir, le nombre de positions libres dans les cinq premières lignes est le même et égal à 2. Par conséquent, l'index de l'une des trois premières lignes est sélectionné au hasard. Dans ce cas, la 12e rangée a été sélectionnée et la position des deux restantes dans cette rangée, ce qui entraîne un minimum de dommages. Ainsi, à la 91e étape de la formation de la solution, nous avons 10 lignes libres: Étape 91-22 (1), 3 (2), 7 (2), 82 (2), 88 (2), 64 (3) 76 (3), 91 (3), 4 (4), 96 (4) . À cette étape, la ligne 22 est sélectionnée et cette position libre qui s'y trouve. En continuant de la même manière, la séquence de décisions suivante a été formée (tableau 1). Les index des lignes sélectionnées sont affichés en gras.

**Tableau 1. Démonstration de l'utilisation de la règle du risque minimum ( n = 100).**
Étape	ligne	ligne	ligne	ligne	ligne	ligne	ligne	ligne	ligne	ligne	ligne
89	25 (1)	12 (2)	22 (2)	82 (2)	7 (3)	64(3)	3(4)	76(4)	91(4)	4(5)	96(5)
90	7(2)	12(2)	22(2)	82(2)	3 (3)	64(3)	76(3)	4(4)	91(4)	96(4)
91	22(1)	3(2)	7(2)	82(2)	64(3)	76(3)	91(3)	4(4)	96(4)
92	88(1)	3(2)	7(2)	82(2)	91(2)	64(3)	76(3)	4(4)	96(4)
93	3(1)	7(2)	76(2)	82(2)	91(2)	4(3)	64(3)	96(4)
94	76(1)	4(2)	7(2)	82(2)	91(2)	64(3)	96(4)
95	91(1)	7(2)	82(2)	64(3)	96(3)
96	4(1)	82(1)	7(2)	64(3)	96(3)
97	7(1)	82(1)	64(2)	96(3)
98	82(1)	64(2)	96(2)
99	64(1)	96(1)
100	64(1)

Dans cet exemple particulier, dans 11 cas sur 12, il y avait une situation où dans la liste des lignes libres restantes il y avait au moins une ligne dans laquelle il ne restait qu'une position libre. Si nous n'utilisions pas la règle du risque minimum, nous ne pourrions pas arriver au bout. Puisqu'un «mauvais coup» dans le choix d'un index d'une ligne libre, cela conduirait très probablement à la destruction de la seule position libre qui se trouvait dans l'une des lignes libres restantes. C'est la raison pour laquelle lorsque vous utilisez uniquement l' algorithme randSet x randSet ou rand x rand pour obtenir une solution complète, dans les dernières étapes, la solution se retrouve dans une impasse.
Il convient de noter que l'algorithme du risque minimum a une signification simple au quotidien et est souvent utilisé dans la prise de décision. Par exemple, le médecin opère tout d'abord sur le patient dont l'état est le plus critique pour la vie, de même, l'agriculteur, lors d'une grave sécheresse, en essayant de sauver la récolte, a tout d'abord arrosé les zones qui sont dans l'état le plus critique ...

7. Analyse de l'efficacité de l'algorithme

Pour évaluer l'efficacité de l'algorithme pour diverses valeurs de n, une expérience de calcul assez longue (en termes de temps total) a été réalisée. Initialement, un algorithme assez rapide a été développé pour générer des tableaux de solutions nQueens Problème pour une valeur arbitraire de n. Ensuite, sur la base de ce programme, de grands échantillons de solutions ont été formés pour une liste de base de n valeurs. Les tailles des échantillons obtenus de solutions nQueens Problème pour différentes valeurs de n, respectivement, étaient égales: (10) - 1000, (20, 30, ..., 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10 000) - -10000, (30000, 50000, 80000) - 5000, (105, 3 * 105) - 3000, (5 * 105, 8 * 105, 106) - 1000, (3 * 106) - 300, ( 5 * 106) - 200, (10 * 106) - 100, (30 * 106) - 50, (50 * 106) - 30, (80 * 106, 100 * 106) - 20. Ici, entre parenthèses, une liste de n valeurs est indiquée, et un double tiret indique la taille de l'échantillon des solutions obtenues.Après cela, des compositions aléatoires de taille arbitraire ont été formées sur la base de chaque échantillon de solutions. Par exemple, pour chacune des 10 000 solutions pour n = 1 000, 100 compositions aléatoires de taille arbitraire ont été formées. Le résultat a été un échantillon d'un million de chansons. Étant donné que toute composition de taille arbitraire, formée sur la base d'une solution existante, peut être complétée au moins une fois jusqu'à une solution complète, la tâche consistait à compléter chaque composition de l'échantillon généré vers une solution complète basée sur l'algorithme de solution n-Queens Completion Problem . Étant donné que dans l'algorithme considéré à chaque étape, le placement correct de la reine sur l'échiquier est vérifié, ici, en principe, elles ne peuvent pas êtredes compositions aléatoires de taille arbitraire ont été formées sur la base de chaque échantillon de solutions. Par exemple, pour chacune des 10 000 solutions pour n = 1 000, 100 compositions aléatoires de taille arbitraire ont été formées. Le résultat a été un échantillon d'un million de chansons. Étant donné que toute composition de taille arbitraire, formée sur la base d'une solution existante, peut être complétée au moins une fois jusqu'à une solution complète, la tâche consistait à compléter chaque composition de l'échantillon généré vers une solution complète basée sur l'algorithme de solution n-Queens Completion Problem . Étant donné que dans l'algorithme considéré à chaque étape, le placement correct de la reine sur l'échiquier est vérifié, ici, en principe, elles ne peuvent pas êtredes compositions aléatoires de taille arbitraire ont été formées sur la base de chaque échantillon de solutions. Par exemple, pour chacune des 10 000 solutions pour n = 1 000, 100 compositions aléatoires de taille arbitraire ont été formées. Le résultat a été un échantillon d'un million de chansons. Étant donné que toute composition de taille arbitraire, formée sur la base d'une solution existante, peut être complétée au moins une fois jusqu'à une solution complète, la tâche consistait à compléter chaque composition de l'échantillon généré vers une solution complète basée sur l'algorithme de solution n-Queens Completion Problem . Étant donné que dans l'algorithme considéré à chaque étape, le placement correct de la reine sur l'échiquier est vérifié, ici, en principe, elles ne peuvent pas être100 compositions aléatoires de taille arbitraire ont été formées. Le résultat a été un échantillon d'un million de chansons. Étant donné que toute composition de taille arbitraire, formée sur la base d'une solution existante, peut être complétée au moins une fois jusqu'à une solution complète, la tâche consistait à compléter chaque composition de l'échantillon généré vers une solution complète basée sur l'algorithme de solution n-Queens Completion Problem . Étant donné que dans l'algorithme considéré à chaque étape, le placement correct de la reine sur l'échiquier est vérifié, ici, en principe, elles ne peuvent pas être100 compositions aléatoires de taille arbitraire ont été formées. Le résultat a été un échantillon d'un million de chansons. Étant donné que toute composition de taille arbitraire, formée sur la base d'une solution existante, peut être complétée au moins une fois jusqu'à une solution complète, la tâche consistait à compléter chaque composition de l'échantillon généré vers une solution complète basée sur l'algorithme de solution n-Queens Completion Problem . Étant donné que dans l'algorithme considéré à chaque étape, le placement correct de la reine sur l'échiquier est vérifié, ici, en principe, elles ne peuvent pas êtreensuite, la tâche consistait à compléter chaque composition de l'échantillon généré, sur la base de l'algorithme de solution n-Queens Completion Problem, à une solution complète. Étant donné que dans l'algorithme considéré à chaque étape, le placement correct de la reine sur l'échiquier est vérifié, ici, en principe, elles ne peuvent pas êtreensuite, la tâche consistait à compléter chaque composition de l'échantillon généré, sur la base de l'algorithme de solution n-Queens Completion Problem, à une solution complète. Étant donné que dans l'algorithme considéré à chaque étape, le placement correct de la reine sur l'échiquier est vérifié, ici, en principe, elles ne peuvent pas êtreDécisions fausses positives (c'est-à-dire décisions incorrectes que nous considérons à tort comme correctes). Cependant, il peut y avoir des solutions fausses négatives - dans le cas où toute composition formée sur la base de la solution existante n'est pas complétée par le programme jusqu'à ce que la solution soit complète (bien que nous sachions que toutes les compositions ont une solution). En effectuant une expérience de calcul dans un si large éventail de valeurs n, nous nous sommes fixés les objectifs suivants:

a) pour déterminer la complexité temporelle de l'algorithme,

b) pour déterminer la probabilité de solutions faussement négatives pour diverses valeurs de n,

c) pour déterminer la fréquence à laquelle la procédure de suivi arrière est utilisée pour différentes valeurs de n.

Les résultats d'une telle expérience de calcul sont présentés dans le tableau 2.

**2. n.**
n – ; m – ; t _mean , t _min , t _max – , ; t90 _mean – , 10% ; FalseNeg( FalseNegative) – , ; *t _row = t _mean *10 ⁶ / n* , 10 ⁶ , *nxn* .
n	m	t _mean	t90 _mean	t _min	t _max	FalseNeg	t _row
10	5000	0.001010	0.000532	0.000168	0.080673	2	1.0102
20	10 ⁵	0.003589	0.001809	0.000197	0.363096	5	1.7945
30	10 ⁵	0.008025	0.003793	0.000244	0.495716	10	2.6752
40	10 ⁵	0.014323	0.009127	0.000252	0.965817	7	3.5807
50	10 ⁵	0.005357	0.003589	0.000313	0.441711	9	10.7146
60	10 ⁵	0.005991	0.004103	0.000340	0.013738	10	9.9852
70	10 ⁵	0.006533	0.004566	0.000368	0.583897	8	9.3328
80	10 ⁵	0.006975	0.004987	0.000394	0.635676	7	8.7187
90	10 ⁵	0.006912	0.004763	0.000393	1.012710	4	7.6840
100	10 ⁵	0.007264	0.005107	0.000419	0.692387	4	7.2641
300	10 ⁵	0.013518	0.009496	0.000986	3.349766	3	4.5060
500	10 ⁵	0.028194	0.014554	0.001541	4.558749	2	5.6388
800	10 ⁵	0.049385	0.022735	0.002367	6.192782	1	6.1731
1000	10 ⁶	0.062157	0.027727	0.002943	8.015123	0	6.2156
3000	10 ⁵	0.177290	0.088507	0.008537	16.713140	0	5.9097
5000	10 ⁵	0.159239	0.136047	0.014224	42.181080	0	3.1849
10 ⁴	10 ⁵	0.321003	0.270927	0.028594	79.321174	0	3.2100
3*10 ⁴	10 ⁴	0.968795	0.651618	0.084936	139.28827	0	3.2293
5*10 ⁴	5000	1.147196	0.864045	0.143005	154.38225	0	2.2944
8*10 ⁴	4000	2.112079	1.215612	0.229532	204.27321	0	2.6401
10 ⁵	2000	2.253118	1.433197	0.290566	224.34623	0	2.2531
3*10 ⁵	2000	4.330649	3.181905	0.990932	340.29584	0	1.4435
5*10 ⁵	2000	5.985339	4.532205	1.488209	382.20016	0	1.1971
8*10 ⁵	2000	8.297512	6.554302	2.902425	75.87513	0	1.0372
10 ⁶	1000	11.376632	7.932194	2.954968	510.6265	0	1.1377
3*10 ⁶	400	23.138609	18.521503	10.433580	122.7597	0	0.7713
5*10 ⁶	300	33.103386	28.057816	14.937556	155.0890	0	0.6621
10*10 ⁶	200	61.444001	52.269241	31.624475	228.3087	0	0.6144
30*10 ⁶	50	149.71717	136.66441	84.556686	352.0534	0	0.4991
50*10 ⁶	40	253.86220	228.93732	105.37934	558.4629	0	0.5077
80*10 ⁶	30	372.29294	341.56397	250.80182	728.4806	0	0.4654
100*10 ⁶	20	508.43573	474.04890	354.80864	831.3753	0	0.5084

La conclusion générale qui peut être tirée sur la base des résultats obtenus est la suivante:

a) L'algorithme fonctionne assez rapidement. Par exemple, le temps moyen de compilation d'une composition arbitraire pour un échiquier de taille 1000 x 1000 , obtenu sur la base d' un million d' expériences informatiques, est de 0,062157 seconde. Cela signifie que si la composition a une solution, elle sera trouvée immédiatement après avoir appuyé sur la touche "Entrée" . Le temps de compilation moyen d'une composition arbitraire, pour toutes les valeurs de n , dans la plage de 7 à 30 000, ne dépasse pas une seconde.

b) Dans chaque échantillon, il y a environ 10% des compositions, qui nécessitent beaucoup plus de temps pour se terminer. De telles compositions forment une longue queue droite dans l'histogramme de distribution. Si nous excluons ces 10% des compositions et effectuons des calculs pour les 90% restants des solutions, alors le temps de calcul ( _moyenne t90 ) sera beaucoup moins. Par exemple, pour un échiquier de 1000 x 1000 , le temps de comptage moyen sera de 0,027727 seconde, ce qui est 2,24 fois inférieur au temps moyen obtenu à partir de l'échantillon entier.

c) Pour les valeurs n≤800 , dans l'échantillon de compositions, il y avait celles qui ne pouvaient pas être complétées avant une solution complète. C'est faux négatifdécisions. Dans les limites spécifiées dans le programme, permettant à la procédure Back Tracking d'être effectuée jusqu'à 1000 fois, l'algorithme n'a pas réussi à terminer ces compositions. Ils ont été classés par erreur comme des compositions négatives, c'est-à-dire ceux qui n'ont pas de solution. Le nombre de ces solutions faussement négatives est insignifiant et leur part dans l'échantillon est inférieure à 0,0001. De plus, lorsque n augmente , la proportion de solutions faussement négatives diminue. Pour toutes les valeurs de n > 800, dans cette série d'expériences de calcul, il n'y avait pas un seul cas de solutions de faux négatifs . Cependant, il est évident que si la taille de l'échantillon est augmentée plusieurs fois, la possibilité d'apparition de faux négatifs n'est pas exclue.solutions, bien que la probabilité d'un tel événement soit très faible.

La complexité temporelle de l'algorithme . La figure 7 montre un graphique des changements dans le temps de prélèvement moyen de compositions aléatoires pour diverses valeurs de n .

Fig.7. La dépendance du temps moyen de cueillette ( t ) des compositions aléatoires de la taille ( n ) de la matrice de décision.

L'axe des abscisses représente le logarithme décimal de la valeur de n , l'axe des ordonnées représente le logarithme, augmenté de 1000 fois, du temps de comptage moyen. Pour plus de clarté, la figure montre également la ligne pointillée de la diagonale du quadrant. On peut voir que le temps de prélèvement augmente linéairement avec une augmentation de n. Sur toute la plage de n valeurs de 50 à 10 ^{8, les} temps de comptage expérimentaux forment une ligne droite, qui avec une corrélation assez élevée ( R = 0,9998 ) est décrite par l'équation de régression linéaire

log (1000 * t) = - 0,628927 + 0,781568 * log (n)

Un léger écart par rapport à la tendance générale n'est caractéristique que pour les valeurs n = (10, ... 49) , ce qui est dû au fait que seul le cinquième bloc de calculs est utilisé dans cette plage pour résoudre le problème, dont l'algorithme diffère considérablement du fonctionnement des algorithmes des premier et troisième blocs. Dans la dépendance obtenue, le coefficient linéaire ( 0,781568 ) est inférieur à l'unité, ce qui conduit au fait qu'avec l'augmentation de n, la droite de régression et la diagonale du quadrant divergent. Afin d'expliquer clairement la raison d'un tel écart au lieu de l'heure initiale, nous considérons le temps moyen nécessaire pour la localisation d'une reine sur une ligne, c'est-à-dire divisez le temps de comptage moyen par n . Nous appelons un tel indicateur le temps réduit.. Évidemment, si le temps réduit ne change pas avec l'augmentation de n , alors une telle solution sera linéaire ( O (n) ). Comme le montre la figure 8, qui montre un tracé du logarithme du temps réduit

Fig.8 La dépendance du temps moyen ( _ligne t ), nécessaire pour que la reine se situe sur une ligne arbitraire, de la taille ( n ) de la matrice de décision.

( tRow ), augmenté de 10 ⁶ fois, à partir du logarithme de la taille de la matrice de solution, dans la plage de n de 50 à 10 ⁸ , le temps réduit diminue avec l'augmentation de n . Si le temps réduit pour n = 50 est 10,7146 * 10 ^-6 secondes, alors le temps correspondant pour n = 10 ^{8 est} réduit de 21 fois et est 0,5084 * 10 ^-6secondes. Un tel comportement de l'algorithme, à première vue, semble erroné, car il n'y a pas de raisons objectives pour lesquelles l'algorithme le considérera plus lent pour les petites valeurs de n que pour les grandes valeurs. Cependant, il n'y a pas d'erreur, et c'est une propriété objective de cet algorithme. Cela est dû au fait que cet algorithme est une composition de trois algorithmes qui fonctionnent à des vitesses différentes. De plus, le nombre de lignes traitées par chacun de ces algorithmes change avec l'augmentation de la valeur de n. C'est pour cette raison que le temps de comptage augmente dans la plage initiale de valeurs n = (10, 20, 30, 40), car tous les calculs dans cette petite zone sont effectués uniquement sur la base du cinquième bloc de procédures, qui fonctionne très efficacement, mais pas aussi rapidement que premier bloc de procédures. Ainsi, étant donné le temps de comptage nécessaire pour positionner la reine sur une ligne,diminue avec l'augmentation de la taille de l'échiquier, la complexité temporelle de cet algorithme peut être appelée décroissante - linéaire.

Le nombre de fois que Back Tracking (BT) a été utilisé . Dans tous les cas d'une expérience de calcul, nous avons suivi le nombre de cas en utilisant la procédure BT pour résoudre chaque problème. Une sommation cumulative a été faite de tous les cas d'utilisation de BT, quel que soit le niveau de base retourné dans le processus de recherche d'une solution. Cela nous a permis de déterminer, pour chaque échantillon, la proportion de ces décisions dans lesquelles la procédure BT n'a jamais été utilisée. La figure 9 montre

Fig.9. La proportion de décisions dans l'échantillon dans lesquelles la procédure de suivi arrière n'a jamais été utilisée dans un

graphique qui montre comment la proportion de cas de la solution change sans utiliser la procédure BT ( Zero Back Tracking ) avec l'augmentation de n . On peut voir que dans la plage de valeurs n = (7, ..., 100000) , le nombre de solutions dans lesquelles la procédure BT n'a jamais été utilisée dépasse 35%. De plus, dans la plage de valeurs n = (320, ..., 22500) , le nombre de tels cas dépasse 50%. Les résultats les plus efficaces ont été obtenus pour un échiquier d'une taille de 5000 x 5000 , où, dans un échantillon de 10 000 compositions, le «déterministe» a été réalisé dans 61,92% des casrésoudre un problème non déterministe , car La procédure BT n'a jamais été utilisée dans 61,92% des cas. Dans les autres solutions, dans 21,87% des cas, la procédure BT a été utilisée 1 fois, dans 9,07% des cas - 2 fois et dans 3,77% des cas - 3 fois. Ensemble, cela représente 96,63% des cas. Le fait qu'après la valeur n = 5000 , le nombre de cas de résolution du problème de configuration sans utiliser la procédure BT diminue progressivement, est associé au modèle sélectionné pour sélectionner les valeurs limites de baseLevel2 et baseLevel3 . Vous pouvez modifier ces paramètres et obtenir une augmentation du nombre de solutions sans utiliser la procédure BT. Cependant, cela entraînera une augmentation du temps de calcul, car la participation du cinquième bloc au fonctionnement de l'algorithme augmentera.

L'histogramme de la distribution de la sélection du temps . Sur la figure 10, pour une valeur de n = 1000 , un histogramme de la distribution du temps de prélèvement pour un million de décisions est présenté. La vue pas tout à fait ordinaire de l'histogramme de distribution (qui ressemble très probablement à la silhouette nocturne de grands immeubles) n'est pas associée à une erreur dans la sélection de la longueur ou du nombre d'intervalles. C'est une propriété naturelle de cet algorithme. Pour comprendre

Fig.10. Un histogramme de l'époque de compilation des compositions de tailles arbitraires. ( n = 1000 ; taille de l'échantillon = 1 000 000 )

pourquoi l'histogramme a cette forme, considérez la distribution du temps de prélèvement pour les compositions qui ont la même taille. Pour cela, à titre d'exemple, dans l'échantillon initial, nous sélectionnerons toutes les compositions dont la taille est de 800. Il y avait 998 compositions de ce type dans un échantillon d'un million. La figure 11 montre un histogramme de la distribution du temps de comptage pour cet échantillon. On peut voir sur la figure que la distribution se compose de six histogrammes distincts, avec des tailles décroissantes.

Fig.11. Un histogramme du temps de compilation de compositions de même taille (k = 800). ( n = 1000 ; taille de l'échantillon = 998 )

La raison pour laquelle le temps de compilation de 998 compositions, dans chacune desquelles 800 reines sont distribuées au hasard, est «regroupé» en 6 groupes, car la procédure de suivi arrière est utilisée. Le premier histogramme de la figure, avec la taille maximale de l'échantillon, est celui des solutions de prélèvement où la procédure BT n'a jamais été utilisée. Il s'agit d'un groupe des solutions les plus rapides. Le deuxième histogramme, qui est beaucoup plus petit que le premier, correspond aux solutions dans lesquelles la procédure BT n'a été utilisée qu'une seule fois. Par conséquent, le temps de décision dans ce groupe est légèrement plus long que dans le premier. En conséquence, dans le troisième groupe, la procédure BT a été utilisée deux fois, dans le quatrième - trois fois, etc., c'est-à-dire Les décisions dans lesquelles la procédure BT a été utilisée à plusieurs reprises ont été prises sur une plus longue période. Ces solutions forment la longue queue droite de la distribution souhaitée.

Solutions fausses négatives . Si nous divisons toutes les compositions possibles pour une valeur arbitraire de nau positif et au négatif, puis parmi les compositions positives il y a celles que cet algorithme peut classer comme négatives. Cela est dû au fait que, dans les limites fixées par les paramètres de recherche, l'algorithme ne peut pas trouver la bonne façon de compléter de telles compositions. Comme le montrent les résultats expérimentaux (tableau 2), le nombre de ces cas ne dépasse pas 0,0001 de la taille de l'échantillon et la valeur de cette erreur diminue avec l'augmentation de n . De plus, pour toutes les valeurs de n> 800, il n'y avait pas un seul cas de solution de faux négatifs . Même l'augmentation de la taille de l'échantillon à un million pour n = 1000 n'a pas donné de faux négatifsdécisions. Le résultat nous permet de formuler la règle suivante pour résoudre le problème: «Toute composition aléatoire de k reines qui est uniformément répartie sur un échiquier arbitraire de taille nxn peut être complétée jusqu'à ce qu'une solution complète soit faite, ou il sera décidé que cette composition est négative et ne peut pas à compléter. La probabilité de prendre une telle décision ne dépasse pas 0,0001 . À mesure que la taille d'un échiquier augmente, la probabilité de prendre des décisions erronées diminue. La complexité temporelle de l'algorithme est linéaire. »

8. Conclusions

1. Un algorithme est présenté qui permet, en temps linéaire, de résoudre le problème d'ensemble complet jusqu'à la solution complète d'une composition aléatoire de k reines, uniformément réparties sur un échiquier de taille arbitraire nxn . De plus, pour toute composition de k reines ( 1≤ k <n ), une solution est apportée, le cas échéant, ou une décision est prise que cette composition ne peut pas être complétée. La probabilité d'une erreur dans la prise d'une telle décision ne dépasse pas 0,0001, et cette valeur diminue avec l'augmentation de la taille d'un échiquier.

2. Le fonctionnement de cet algorithme est basé sur l'utilisation de deux règles importantes:

a) Au stade final de la résolution du problème, parmi toutes les lignes libres restantes, une est sélectionnée pour laquelle le nombre de positions libres est minimal ( règle du risque minimum ). Cela minimise les risques liés à la possibilité d'exclure les dernières positions vacantes dans certaines des lignes restantes.

b) De tous les postes vacants dans la ligne en question, cette position est sélectionnée, ce qui cause un minimum de dommages aux positions libres dans les lignes libres restantes ( règle du minimum de dégâts ). Par « dommage minimal », on entend la sélection d'une telle position dans une ligne qui exclut le moins de positions libres dans toutes les lignes libres restantes.

3. Il a été établi qu'à la suite du fonctionnement de cet algorithme, le temps moyen nécessaire pour que la reine soit placée sur une ligne diminue avec l'augmentation de la valeur de n. Le temps moyen nécessaire pour placer la reine sur une ligne dans le cas où n est 10 ⁸ est 21 fois inférieur au temps correspondant pour le cas n = 50.

4. Il a été constaté que dans la plage de valeurs n = (7, ..., 100000), le nombre de solutions dans lesquelles la procédure de suivi arrière n'a jamais été utilisée dépasse 35%. De plus, dans la plage de valeurs n = (320, ..., 22500) , le nombre de tels cas dépasse 50%, ce qui indique la grande efficacité de cet algorithme.

5. Un modèle d'organisation de la procédure de suivi arrière est proposé., basé sur la séparation de la séquence des étapes de la décision aux niveaux de base. Un niveau signifie une certaine étape de décision avec un nombre donné de reines correctement placées . Des formules de régression sont données pour calculer les valeurs des deuxième et troisième niveaux de base en fonction de n .

6. Les résultats d'une analyse comparative de deux méthodes de sélection aléatoire, appelées randSet & randSet et rand & rand , sont présentés . L' algorithme randSet & randSet s'est avéré rapide, mais grossier. Par conséquent, son utilisation est limitée en atteignant le deuxième niveau de base. Après cela, l'algorithme rand & rand est utilisé., qui n'est pas si rapide, mais qui place plus efficacement les reines sur un échiquier.

7. Un algorithme efficace pour vérifier l'exactitude de la solution du problème n-Queens est donné . Ce programme est également conçu pour vérifier l'exactitude d'une composition aléatoire de taille arbitraire. Le programme fonctionne assez rapidement. Par exemple, le temps requis pour valider une solution composée de 5 millions de positions est de 0,85 seconde.

9. Commentaires

1. Comme indiqué au début de l'article, des études ont été menées dans la plage de n valeurs , de 7 à 100 millions. Cependant, le programme a été testé dans une gamme plus large de valeurs n , jusqu'à un milliard. Certes, dans ce dernier cas, le programme a dû être légèrement adapté, compte tenu de la grande taille des tableaux. Par conséquent, si la taille de la RAM le permet, il est possible d'effectuer des calculs pour de grandes valeurs de n.

2. Les valeurs des indicateurs de base, ainsi que les valeurs limites du nombre de répétitions à différents niveaux, ont été optimisées pour résoudre le problème dans l'ensemble de la plage de recherche. Ils peuvent être modifiés dans une plage plus petite et réduire le temps de comptage. Il est important de ne pas augmenter la part des solutions de faux négatifs .

3. Dans cet article, j'ai utilisé le temps de pression de la touche Entrée comme mesure du temps pour évaluer la vitesse de fonctionnement de l'algorithme. Si le résultat apparaît immédiatement après avoir appuyé sur la touche, alors au niveau de la perception de l'utilisateur, il semble que le programme fonctionne "très" rapidement. Quelle que soit la vitesse à laquelle l'algorithme fonctionne, le résultat n'apparaîtra pas à l'écran tant que la clé n'est pas terminée. Par conséquent, il m'a semblé qu'une telle mesure conditionnelle du temps pouvait servir de seuil pour ne pas comparer strictement la vitesse de divers algorithmes.

4. Philosophique ... Au cours de l'étude, un grand nombre de publications liées à la solution de problèmes non déterministes ont été examinées. Dans la plupart des cas, il s'agissait de tâches dans lesquelles il était nécessaire de faire un choix dans un large espace d'États dans des conditions de restrictions données. En les comparant, il était intéressant de savoir jusqu'où on peut avancer dans la résolution de ces problèmes en utilisant l'approche mathématique standard. J'ai eu l'impression qu'il est impossible de résoudre de tels problèmes uniquement sur la base de définitions, d'énoncés de lemmes et de preuves de théorèmes. Il me semble que pour résoudre de tels problèmes, il est nécessaire d'utiliser les méthodes des mathématiques algorithmiques en utilisant la simulation informatique. Pour démontrer la validité de cette conclusion, à titre d'exemple simple, je me suis préparé pour un échiquier dont la taille est de 10⁹ x 10 ⁹ deux compositions de même taille, composées de 999 999 482 reines. Ils sont préparés comme décrit au début de l'article et sont présentés sous forme de deux fichiers au format .mat. Ils peuvent être téléchargés sur ce lien (deux fichiers de test) . Les fichiers sont assez "lourds", la taille de chacun d'eux est d'environ 3,97 Go. Dans 999 997 976 lignes (dans 99,9998% des cas), les positions des reines dans les deux compositions coïncident, et ce n'est que dans 1506 lignes arbitraires que les positions des reines diffèrent.

Pour compléter les données de composition en une solution complète, vous devez placer correctement les reines dans les 518 lignes libres restantes. Le nombre de façons possibles d'organiser 518 reines dans les lignes libres restantes (en tenant compte uniquement du nombre de façons de sélectionner une position libre dans la ligne sélectionnée) est d'environ 10 ^1466.. La différence entre ces deux compositions est seulement que l'une d'entre elles est positive et peut être complétée jusqu'à une solution complète, et l'autre composition est négative - elle ne peut pas être complétée jusqu'à ce qu'une solution complète. Question: «Est-il possible, sur la base d'une approche mathématique rigoureuse (c'est-à-dire sans effectuer d'opérations algorithmiques de calcul), de déterminer laquelle de ces deux compositions est positive?» Si cela est impossible à résoudre, alors nous pouvons supposer que la proposition faite est prouvée par la contradiction.

Je veux noter que quelle que soit l'approche de la solution strictement mathématique à ce problème, il est nécessaire de déterminer le statut 518 * 10 ⁹cellules dans les lignes libres restantes. Pour ce faire, il est nécessaire de considérer chaque position de reines précédemment établies, et il y en a près d'un milliard, afin d'établir les restrictions que chaque reine établie impose aux positions libres dans les 518 lignes restantes. Je n'ai pas trouvé de «point d'appui» qui me permettrait de faire ce travail uniquement sur la base d'une approche strictement mathématique, sans calculs algorithmiques.

J'ai donné ici un exemple minimal composé de seulement deux compositions. Si nécessaire, le nombre de ces compositions peut être augmenté.

Il convient de noter que sur la base de l'algorithme linéaire proposé, légèrement adapté pour travailler avec de grandes compositions, dont les tâches des deux compositions de test peuvent être achevées jusqu'à ce qu'une solution complète soit effectuée sur le bureau-13 , en environ 4,5 minutes (hors temps de chargement des données d'entrée).

10. Addition

L'action des professeurs qui recommandent aux étudiants des tâches capables de se développer et de faire des recherches est digne de respect. Cela nécessite des efforts considérables, mais en surmontant les difficultés, le chercheur envisage différemment d'autres tâches complexes. J'ai pensé qu'il serait utile d'étendre les options pour régler le problème des n-reines à de telles fins. Si vous regardez la même tâche sous différents angles, vous pouvez voir différentes choses. En voici quelques-uns.

1. Considérez le problème de disposer n reines sur un échiquier rectangulaire de taille nxm . Notons k = m - n . Soit une solution obtenue, et dans chacun des nIl y avait une reine dans chaque rangée. Nous excluons les postes où se trouvent des reines de toute considération ultérieure. Maintenant, dans chaque ligne, il y a m-1 position libre. Dans les positions libres restantes, nous trouvons à nouveau une solution. Comme précédemment, nous excluons de plus ample examen les positions où se trouvent les reines de la seconde solution. Maintenant, dans chaque rangée, il y a m-2 positions libres. De toute évidence, les première et deuxième solutions ne se croisent pas dans leurs positions dans aucune rangée - elles sont orthogonales. Il est nécessaire de déterminer le nombre maximal de solutions mutuellement orthogonales pour différentes valeurs de k . Si n solutions mutuellement orthogonales sont trouvées pour la valeur k = 0alors la place royale latine sera construite.

Remarque . Le document Grigoryan E. (2018) ont montré que , pour toute solution problème de n-Queens il existe une solution complémentaire, qui ne gêne pas avec elle. Cela signifie que pour une valeur arbitraire de n , l'ensemble de toutes les solutions du problème des n-reines est divisé en deux sous - ensembles de taille égale . Toute solution du deuxième sous-ensemble est une solution complémentaire à la solution correspondante du premier sous-ensemble. La règle est assez simple, si Q1 (i) est une solution du premier ensemble, alors la solution complémentaire correspondante Q2 (i)à partir du deuxième sous-ensemble est déterminé par la formule Q2 (i) = n + 1 - Q1 (i), où i = (1, ..., n) . C'est cette règle qui explique le fait que le nombre de toutes les solutions du problème des n-reines , pour une valeur arbitraire de n , est toujours un nombre pair. (Cette règle nous permet de diviser par deux le temps de calcul de toutes les solutions complètes pour une taille arbitraire n de l' échiquier. Si nous notons 2 * k le nombre total de toutes les solutions, la valeur k est égale à l'index dans la liste séquentielle de toutes les solutions lorsque Q (k) + Q ( k + 1) = n + 1 ).

2. Dans la formulation initiale du problème Problème n-Qeens , après que la reine soit placée en position (i, j), les actions suivantes sont effectuées:

a) toutes les cellules de la ligne i et de la colonne j

sont exclues; b) toutes les cellules situées sur la ligne des diagonales gauche et droite passant par la cellule (i, j) sont exclues .

Nous modifions la condition b) dans l'énoncé du problème. Au lieu d'éliminer les cellules, nous utiliserons la commutation de cellules. Si la cellule située sur la ligne des diagonales gauche ou droite est libre, nous la fermerons; si la cellule est fermée, nous l'ouvrirons. Cela facilite la recherche d'une solution. Cependant, au lieu de la matrice carrée nxn , nous considérons une matrice rectangulaire de taille nx (n - k) . Il faut, pour une valeur donnée de n , trouver la valeur maximale de kà laquelle au moins trois solutions orthogonales peuvent être obtenues. Comment la valeur de k changera-t-elle avec l'augmentation de la valeur de n ?

3. Modifiez certaines conditions dans la formulation initiale du problème du problème des n-reines . Lorsque la reine est positionnée en position (i, j) sur un échiquier de taille nxn :

a) nous excluons toutes les cellules de la ligne i ,

b) si l'index j est un nombre pair, alors:

b1) nous excluons les cellules des lignes paires de la colonne j,

b2) nous excluons les cellules de lignes paires coupant les diagonales gauche et droite passant par la cellule (i, j) ,

c) Si l'indice jnombre impair, alors les éléments b1) et b2) sont satisfaits pour les cellules situées sur des lignes impaires.

3.1 On sait (Sloane-2016) que la liste des valeurs de toutes les solutions du problème nQueens , pour n = (8, 9, 10, 11, 12, 13, 14, 15, 16) , respectivement, est (92, 352, 724, 2680, 14200, 73712, 365596, 2279184, 14772512) . Comment le nombre de toutes les solutions changera-t-il si, dans l'énoncé du problème, la condition standard pour les exceptions diagonales est remplacée par le paragraphe b) ou le paragraphe c)?

3.2 Il est connu par Grigoryan (2018) que si nous déterminons la fréquence de participation des différentes cellules de la matrice de décision à la formation d'une liste de toutes les solutions, nous pouvons constater qu'il existe des relations harmonieuses entre toutes les cellules sous la forme de symétries verticales et horizontales des fréquences correspondantes. Cela signifie que si nous supposons que k <n / 2 , alors la fréquence des cellules de la k-ème ligne sera identique aux fréquences des cellules de la ligne n-k + 1 . De même, la fréquence des cellules de la k-ème colonne sera identique aux fréquences des cellules de la colonne n-k + 1 . Question: «Comment ces relations harmonieuses changeront-elles dans le contexte de la tâche?»

4. Toutes les cellules d'un échiquier sont divisées en deux classes par leur couleur. On pense qu'une couleur est blanche, l'autre est noire. Considérez deux échiquiers et placez l'un d'eux sur l'autre de sorte que les bords coïncident complètement. En conséquence, nous obtenons un "sandwich" de deux échiquiers, dans lesquels la disposition des cellules blanches et noires coïncident. La tâche consiste à trouver des solutions simultanément sur deux planches, en respectant les conditions suivantes:

a) Si sur l'une des planches la reine est sur une cellule noire avec des indices (i, j) , alors:

- sur les deux planches toutes les cellules noires qui se produisent sur la ligne i et la colonne j ,

- sur les deux planches, toutes les cellules noires situées le long des diagonales gauche et droite traversant la cellule (i, j) sont exclues .

b) Si sur l'une des planches la reine se trouve sur un globule blanc avec des indices (i, j) , alors toutes les actions du paragraphe a) sont effectuées uniquement pour les globules blancs.

5. Imaginez que dans une matrice de solution de taille nxn , les rangées puissent glisser les unes par rapport aux autres à droite ou à gauche, avec un pas de k cellules. De plus, si la ligne précédente a été décalée, par exemple, vers la gauche, la ligne suivante doit être décalée vers la droite, c'est-à-dire chaque ligne suivante est décalée dans la direction opposée à la ligne précédente. Grâce à cette construction, nous obtenons une matrice rectangulaire de taillenx (n + k) , où dans chaque ligne, k cellules du début de la ligne ou de la fin seront exclues de la considération. La tâche consiste à trouver la valeur maximale de k pour une valeur arbitraire de n pour laquelle il existe au moins une solution n-Queens Problem . Considérons une variante du problème dans laquelle le décalage d'une ligne par rapport à une autre est un nombre aléatoire allant de k1 à k2 . 6. La formulation unidimensionnelle du problème nQueens . Soit n segments de longueur arbitraire, numérotés de 1 à n , disposés sur le demi-axe . Divisez chaque segment par n

les cellules de taille arbitraire, et dans chaque segment, numérotent les cellules de 1 à n . Nous appelons ces cellules ouvertes. Il faut près d' une cellule sur chaque segment, compte tenu des limitations suivantes:

a) Nous pouvons choisir une cellule ouverte avec l' indice j du i ème segment si:

D1 (r) = 0;

D2 (t) = 0;

où r = n + j - i, t = j + i, D1 et D2 sont des réseaux de contrôle unidimensionnels composés de 2n cellules qui ont été précédemment mises à zéro.

b) Après ce choix, le segment i et les cellules portant le numéro j seront fermésdans tous les segments libres restants. Il est également nécessaire de fermer les cellules correspondantes dans les tableaux de contrôle:

D1 (r) = 1;

D2 (t) = 1;

Dans ce paramètre, la tâche est complètement identique à celle d'origine. La formulation de ce problème avec d'autres conditions de contrainte est intéressante. Par exemple, si au lieu des formules:
r = n + j - i, t = j + i, ,
seront pris en considération d' autres rapports, qui sont des indices fonctionnellement associés r et t indices (i, j) faisant une matrice.

7. Le libellé de la tâche sur la base d'une urne à billes (identique au libellé précédent). Supposons qu'il y ait n urnes numérotées de 1 à n, et dans chaque urne il y a n boules, également numérotées de 1 à n . Nécessite une urne à une distance l'une de l'une bille, compte tenu des limitations ci - après:

a) on peut sélectionner le ballon avec le nombre j de la i ème urne si:

D1 (r) = 0 ,

D2 (t) = 0 ,

où r = n + j - i, t = j + i, D1 et D2 sont des réseaux de contrôle unidimensionnels composés de 2n cellules qui ont été précédemment mises à zéro.

b) Après ce choix, l'urne i et les balles portant le numéro j seront fermées dans toutes les urnes libres restantes. Il est également nécessaire de fermer les cellules correspondantes dans les tableaux de contrôle:

D1 (r) = 1 ,

D2 (t) = 1 .

Dans ce paramètre, la tâche est complètement identique à celle d'origine. Comme dans le cas précédent, l'énoncé de ce problème avec d'autres conditions qui relient fonctionnellement les indices r et t aux indices (i, j) de la matrice de décision est intéressant .

8. Le jeu . Prenons un échiquier de taille nxn . Rendons la couleur aux reines, laissons certaines reines avoir une couleur blanche, d'autres noires. Nous renvoyons également l'alternance de couleur blanche et noire aux cellules de l'échiquier, en se basant sur le fait que la cellule avec l'index (1, n)devrait être blanc. Toutes les cellules au début du jeu sont considérées comme libres. Les reines blanches font le premier pas. Le joueur place la reine dans une cellule libre arbitraire avec des indices (i, j) . Que ce soit un globule blanc. À la suite de ce choix, ils sont fermés:

a) tous les globules blancs de la ligne i ,

b) tous les globules blancs de la colonne j ,

c) tous les globules blancs qui se trouvent sur les diagonales gauche et droite traversant la cellule (i, j) .

Si la cellule (i, j) s'avère noire, alors tous les points (a, b, c) sont satisfaits, et en conséquence, toutes les cellules de couleur noire sont fermées. Ensuite, Black effectue le mouvement, plaçant la reine dans l'une des cellules libres restantes. Après cela, d'une manière similaire, les cellules se ferment, comme décrit ci-dessus. Le temps de réflexion sur le prochain mouvement est fixe et est choisi avec l'accord des parties. Si pendant le temps spécifié, l'un des joueurs ne termine pas son coup, le jeu est transféré à l'autre. La partie se termine si les deux joueurs, l'un après l'autre, ne parviennent pas à terminer leur tour dans le temps imparti. Celui qui peut placer plus de reines sur le plateau gagne.

9. Sur la stabilité de la sélection aléatoire. Prenons le modèle randSet & randSet . Grâce à la comparaison de n paires aléatoires d'indices de ligne et de colonne, au premier stade du cycle, il est possible d'établir les reines en moyenne àk * n lignes. La valeur de k peut être considérée comme une valeur constante égale à 0,6. Sa valeur varie de 0,605701 à n = 10 , et à 0,599777, à n = 10 ⁶ et, avec l'augmentation de n , la variance de cette valeur diminue. Quelle est la raison d'une telle "constance"? Pourquoi, avec une sélection aléatoire de l'index des lignes et de l'indice de position de la reine dans cette ligne, sur la base de deux listes de nombres obtenues sur la base d'une permutation aléatoire des nombres de 1 à n, il est possible de placer systématiquement les reines (en moyenne) sur 60% des lignes?

10. Que la taille de l'échiquier soit nxn . Basé sur la procédure randSet & randSetplacez les reines sur l'échiquier jusqu'à ce que la branche de recherche atteigne une impasse. Notons la longueur de la composition ainsi obtenue par k . Si, pour une valeur donnée de n, répétez cette procédure plusieurs fois, et construisez un histogramme de la distribution des valeurs de k , il s'avère que le changement de la fréquence d'occurrence des événements à la valeur du mode de distribution diffère du changement de la fréquence d'occurrence des événements après cette valeur. Si, sur la base de la valeur modale, l'histogramme est divisé en deux parties, la partie gauche ne coïncidera pas avec la partie droite. Ce modèle est caractéristique pour toute valeur de n. Pourquoi, après le passage de la longueur de la composition à la valeur modale, la fréquence d'apparition des événements prend-elle une forme différente? Par événement, nous entendons recevoir une composition d'une taille donnée, avant d'atteindre un état d'impasse.

Littérature

1. Nauck, F. (1850). Briefwechsel mit allen fur alle . Illustrierte Zeitung, 15, 182.

2. Gent, IP, Jefferson, C. & Nightingale, P. (2017). Complexité de l'achèvement de n-Queens ,
Journal of Artificial Intelligence Research., 59, 815-848.

3. Sosic, R. et Gu, J. (1990). Un algorithme de temps polynomial pour le problème des n-reines . Bulletin SIGART, 1 (3), 7–11.

4. Richards, M. (1997). Algorithmes de retour en arrière dans MCPL utilisant des modèles de bits et la récursivité .
Tech. rep., Laboratoire d'informatique, Université de Cambridge.

5. Méthodes de randomisation dans la conception d'algorithmes , Proceedings of a DIMACS Workshop, Princeton, New Jersey, USA, December 12-14, 1997. DIMACS Series in Discrete Mathematics and Theoretical Computer Science 43, DIMACS/AMS 1999, ISBN 978-0-8218-0916-7

6. Grigoryan E. (2018). Investigation of the Regularities in the Formation of Solutions n-Queens Problem . Modeling of Artificial Intelligence, 5(1), 3-21

7. Sloane N.-JA (2016). The on-line encyclopedia of integer sequences.

n-Queens Completion Problem - algorithme de solution linéaire