Présentation de la méthode de rétropropagation

Bonjour à tous! Les vacances du Nouvel An ont pris fin, ce qui signifie que nous sommes à nouveau prêts à partager du matériel utile avec vous. Une traduction de cet article a été préparée en prévision du lancement d'un nouveau volet sur le cours "Algorithmes pour les développeurs" .

C'est parti!

---

La méthode d'erreur de propagation inverse est probablement l'élément le plus fondamental d'un réseau neuronal. Il a été décrit pour la première fois dans les années 1960 et près de 30 ans plus tard, il a été popularisé par Rumelhart, Hinton et Williams dans un article intitulé «Apprendre les représentations par des erreurs de propagation inverse» .

La méthode est utilisée pour entraîner efficacement un réseau de neurones en utilisant la règle dite de la chaîne (la règle de différenciation d'une fonction complexe). Autrement dit, après chaque passage à travers le réseau, la propagation arrière effectue un passage dans la direction opposée et ajuste les paramètres du modèle (poids et déplacements).

Dans cet article, je voudrais examiner en détail d'un point de vue mathématique le processus d'apprentissage et d'optimisation d'un réseau neuronal simple à 4 couches. Je pense que cela aidera le lecteur à comprendre le fonctionnement de la rétropropagation et à en comprendre l'importance.

Définir un modèle de réseau neuronal

Le réseau neuronal à quatre couches se compose de quatre neurones dans la couche d'entrée, de quatre neurones dans les couches cachées et d'un neurone dans la couche de sortie.


Une image simple d'un réseau neuronal à quatre couches.

Couche d'entrée

Sur la figure, les neurones violets représentent l'entrée. Ils peuvent être de simples quantités scalaires ou plus complexes - des vecteurs ou des matrices multidimensionnelles.


Équation décrivant les entrées xi.

Le premier ensemble d'activations (a) est égal aux valeurs d'entrée. «Activation» est la valeur d'un neurone après application de la fonction d'activation. Voir ci-dessous pour plus de détails.

Couches masquées

Les valeurs finales dans les neurones cachés (dans la figure verte) sont calculées en utilisant les entrées pondérées z ^l dans la couche I et les activations a ^I dans la couche L. Pour les couches 2 et 3, les équations seront les suivantes:

Pour l = 2:



Pour l = 3:



W ² et W ³ sont les poids sur les couches 2 et 3, et b ² et b ³ sont les décalages sur ces couches.

Les activations a ² et a ³ sont calculées à l'aide de la fonction d'activation f. Par exemple, cette fonction f est non linéaire (comme sigmoïde , ReLU et tangente hyperbolique ) et permet au réseau d'étudier des motifs complexes dans les données. Nous ne nous attarderons pas sur le fonctionnement des fonctions d'activation, mais si vous êtes intéressé, je vous recommande fortement de lire ce merveilleux article .

Si vous regardez attentivement, vous verrez que tous les x, z ² , a ² , z ³ , a ³ , W ¹ , W ² , b ¹ et b ² n'ont pas d'indices représentés sur la figure d'un réseau neuronal à quatre couches. Le fait est que nous avons combiné toutes les valeurs des paramètres dans des matrices regroupées par couches. C'est une façon standard de travailler avec les réseaux de neurones, et c'est assez confortable. Cependant, je vais parcourir les équations pour qu'il n'y ait pas de confusion.

Prenons l'exemple de la couche 2 et de ses paramètres. Les mêmes opérations peuvent être appliquées à n'importe quelle couche du réseau neuronal.
W ¹ est la matrice des poids de dimension (n, m) , où n est le nombre de neurones de sortie (neurones dans la couche suivante), et m est le nombre de neurones d'entrée (neurones dans la couche précédente). Dans notre cas, n = 2 et m = 4 .



Ici, le premier nombre dans l'indice de l'un des poids correspond à l'indice des neurones dans la couche suivante (dans notre cas, c'est la deuxième couche cachée), et le deuxième nombre correspond à l'indice des neurones dans la couche précédente (dans notre cas, c'est la couche d'entrée).

x est le vecteur d'entrée de dimension ( m , 1), où m est le nombre de neurones d'entrée. Dans notre cas, m = 4.



b ¹ est le vecteur de déplacement de dimension ( n , 1), où n est le nombre de neurones dans la couche actuelle. Dans notre cas, n = 2.



En suivant l'équation pour z ^2, nous pouvons utiliser les définitions ci-dessus de W ¹ , x et b ¹ pour obtenir l'équation z ² :



Regardez maintenant attentivement l'illustration du réseau de neurones ci-dessus:



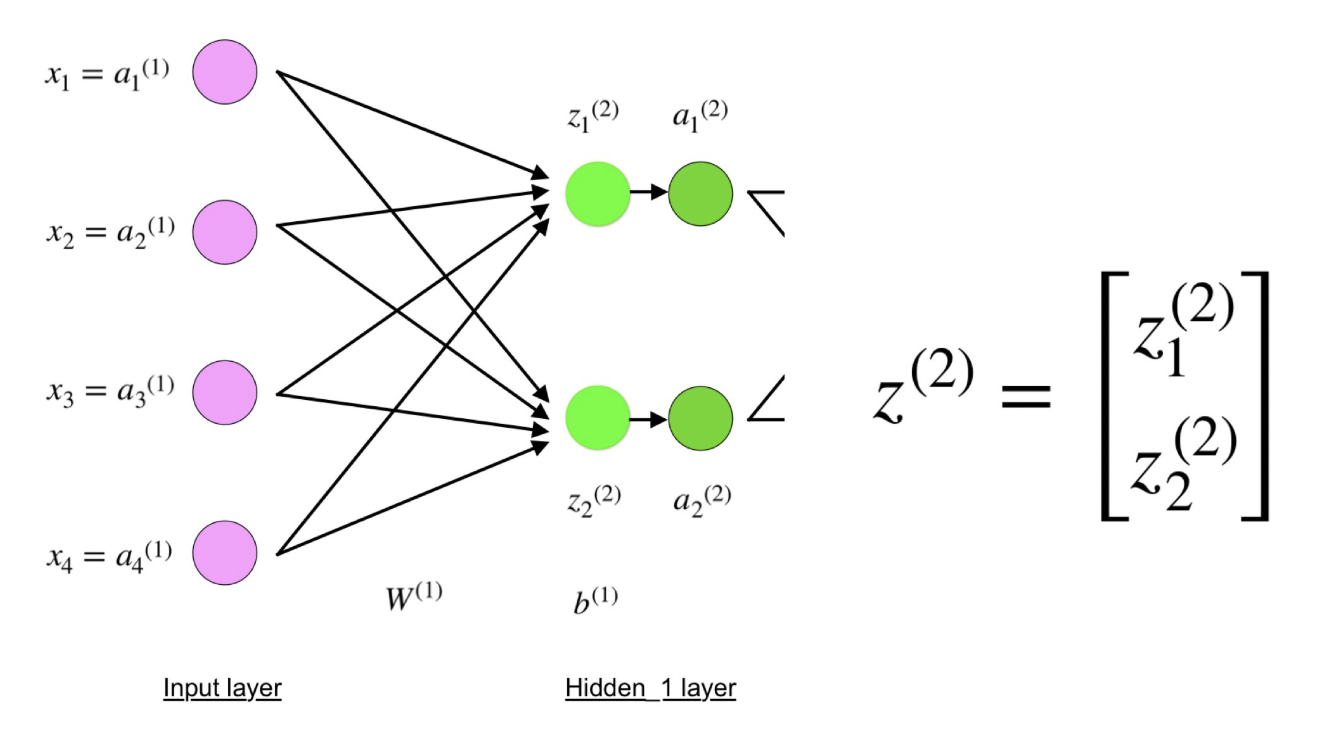
Comme vous pouvez le voir, z ² peut être exprimé en termes de z ₁ ² et z ₂ ² , où z ₁ ² et z ₂ ² sont les sommes des produits de chaque valeur d'entrée x ⁱ par le poids correspondant W _ij ¹ .

Cela conduit à la même équation pour z ² et prouve que les représentations matricielles z ² , a ² , z ³ et a ³ sont vraies.

Couche de sortie

La dernière partie du réseau neuronal est la couche de sortie, qui donne la valeur prédite. Dans notre exemple simple, il se présente sous la forme d'un seul neurone coloré en bleu et calculé comme suit:



Encore une fois, nous utilisons la représentation matricielle pour simplifier l'équation. Vous pouvez utiliser les méthodes ci-dessus pour comprendre la logique sous-jacente.

Distribution directe et évaluation

Les équations ci-dessus forment une distribution directe à travers le réseau neuronal. Voici un bref aperçu:



(1) - couche d'entrée
(2) - la valeur du neurone dans la première couche cachée
(3) - valeur d'activation sur la première couche cachée
(4) - la valeur du neurone dans la deuxième couche cachée
(5) - valeur d'activation au deuxième niveau caché
(6) - couche de sortie

La dernière étape du passage direct consiste à évaluer la valeur de sortie prédite s par rapport à la valeur de sortie attendue y .

La sortie y fait partie de l'ensemble de données d'apprentissage (x, y), où x est l'entrée (comme nous le rappelons de la section précédente).

L'estimation entre s et y s'effectue via la fonction de perte. Elle peut être simple comme erreur standard ou plus complexe comme entropie croisée .

Nous appelons cette fonction de perte C et la notons comme suit:



Où le coût peut être égal à l'erreur standard, à l'entropie croisée ou à toute autre fonction de perte.

Sur la base de la valeur de C, le modèle «sait» combien ses paramètres doivent être ajustés afin d'approcher la valeur de sortie attendue de y . Cela se produit en utilisant la méthode de rétropropagation.

Propagation de l'erreur et calcul des gradients

Basée sur un article de 1989, la méthode de rétropropagation:

Ajuste constamment les poids des connexions dans le réseau pour minimiser la mesure de la différence entre le vecteur de sortie réel du réseau et le vecteur de sortie souhaité .
et
... permet de créer de nouvelles fonctions utiles qui distinguent la rétropropagation des méthodes antérieures et plus simples ...

En d'autres termes, la rétropropagation vise à minimiser la fonction de perte en ajustant les poids et les décalages du réseau. Le degré d'ajustement est déterminé par les gradients de la fonction de perte par rapport à ces paramètres.

Une question se pose: pourquoi calculer des gradients ?

Pour répondre à cette question, nous devons d'abord réviser certains concepts de l'informatique:

Le gradient de la fonction C (x ¹ , x ² , ..., x ^m ) en x est le vecteur des dérivées partielles de C par rapport à x .



La dérivée de la fonction C reflète la sensibilité à un changement de la valeur de la fonction (valeur de sortie) par rapport au changement de son argument x ( valeur d'entrée ). En d'autres termes, la dérivée nous indique dans quelle direction C. se déplace.

Le gradient montre combien il est nécessaire de changer le paramètre x (dans le sens positif ou négatif) afin de minimiser C.

Ces gradients sont calculés à l'aide d'une méthode appelée règle de chaîne.
Pour un poids (w ^jk ) _{l, le} gradient est:



(1) Règle de chaîne
(2) Par définition, m est le nombre de neurones par l - 1 couche
(3) Calcul dérivé
(4) Valeur finale
Un ensemble d'équations similaire peut être appliqué à (b ^j ) _l :



(1) Règle de chaîne
(2) Calcul dérivé
(3) Valeur finale
La partie commune des deux équations est souvent appelée «gradient local» et s'exprime comme suit:



Un «gradient local» peut être facilement déterminé à l'aide d'une règle de chaîne. Je ne peindrai pas ce processus maintenant.

Les dégradés permettent d'optimiser les paramètres du modèle:

Jusqu'à ce que le critère d'arrêt soit atteint, les opérations suivantes sont effectuées:



Algorithme d'optimisation des poids et des décalages (également appelé descente de gradient)

• Les valeurs initiales de w et b sont sélectionnées au hasard.
• Epsilon (e) est la vitesse d'apprentissage. Il détermine l'effet du dégradé.
• w et b sont des représentations matricielles de poids et de décalages.
• La dérivée de C par rapport à w ou b peut être calculée en utilisant des dérivées partielles de C par rapport aux poids ou compensations individuels.
• La condition de terminaison est satisfaite dès que la fonction de perte est minimisée.

Je veux consacrer la dernière partie de cette section à un exemple simple dans lequel nous calculons le gradient C par rapport à un poids (w ²² ) ₂ .

Zoomons sur le bas du réseau neuronal susmentionné:



Représentation visuelle de la rétropropagation dans un réseau neuronal
Le poids (w ²² ) ₂ relie (a ² ) ₂ et (z ² ) ₂ , donc le calcul du gradient nécessite d'appliquer la règle de chaîne sur (z ² ) ₃ et (a ² ) ₃ :



Le calcul de la valeur finale de la dérivée de C de (a ² ) ₃ nécessite la connaissance de la fonction C. Puisque C dépend de (a ² ) ₃ , le calcul de la dérivée doit être simple.

J'espère que cet exemple a réussi à faire la lumière sur les mathématiques derrière le calcul des gradients. Si vous voulez en savoir plus, je vous recommande fortement de consulter la série d'articles Stanford NLP, où Richard Socher fournit 4 excellentes explications pour la rétropropagation.

Remarque finale

Dans cet article, j'ai expliqué en détail comment la rétropropagation d'une erreur fonctionne sous le capot en utilisant des méthodes mathématiques telles que le calcul des gradients, la règle de chaîne, etc. Connaître les mécanismes de cet algorithme renforcera votre connaissance des réseaux de neurones et vous permettra de vous sentir à l'aise lorsque vous travaillez avec des modèles plus complexes. Bonne chance dans votre parcours d'apprentissage en profondeur!

C’est tout. Nous invitons tout le monde à un webinaire gratuit sur le thème "Arbre de segments: simple et rapide" .