Soleil, vent et eau ver 0,2

Saison deux

Physique du yachting ou du yachting pour les physiciens

Au cours de la formation à l’école du timonier, des praticiens expérimentés nous ont expliqué comment les vrais plaisanciers voient le vent «rose», ressentent le bon angle en un seul endroit et ne sont pas affectés par le crétinisme spatial. Apparemment, l'éducation dans le domaine de la physique empêche une personne de voir des vents "roses" et rend un endroit moins sensible. Je vais essayer de comprendre comment le yacht se déplace en nombre.

De quoi avez-vous besoin pour numériser un yacht?

1. Caractéristique de remorquage
   
2. Tableau de stabilité
   
3. Géométrie de la voile - mesure en direct
   la hauteur de l'angle supérieur de la grotte $$$h_ {gr top} = 11,2 m$ ;
   hauteur de l'angle d'amure de la grotte $$$h_ {gr hls} = 1 985 m$ ;
   angle d'écoute $$$h_ {gr pc} = 2,179 m$ ;
   distance de l'angle d'écoute de la grand-voile par rapport au mât $$$l_ {gr pc} = 2,96 m$ ;
   hauteur de l'angle supérieur de la trinquette $$$h_ {st top} = 10 m$ ;
   Hauteur d'agrafage de l'empileur $$$h_ {st sls} = 1 111 m$ ;
   angle d'écoute $$$h_ {cst} = 1,5 m$ ;
   zone de la grotte $$$S_ {gr} = 17,2 m ^ 2$ ;
   zone de trinquette $$$S_ {st} = 14 m ^ 2$ ;
   zone latérale de voile de coque $$$S_ {anf} = 7,315 m ^ 2$ ;
   zone de dérive frontale de la coque $$$S_ {fr} = 3 m ^ 2$ ;
   projection latérale de la zone du corps sous-marin $$$S_ {dn} w = 1,82 m ^ 2$ ;
   zone de quilles et skegs $$$S_ {ks} = 2,33 m ^ 2$ ;
   angle minimum de trinquette possible $$$\ psi_ {ct} = 18 ^ o$ .
   
   Peut-être que j'ai été si malchanceux, mais aucun des fabricants, lors de ma recherche du yacht, n'a accepté (ne pouvait pas) fournir ces données pour leur yacht. Je suis sûr que le concepteur du yacht possède toutes ces informations, mais pour une raison quelconque, je ne peux pas les obtenir. Je l'exploiterai moi-même.
   J'ai déjà reçu la caractéristique de remorquage en numérisant le yacht dans le programme de freeship . En récompense de la persévérance, le programme donne immédiatement à la fois un diagramme de stabilité et un point de centre de gravité et un centre de traînée latérale, et de nombreuses autres informations géométriques utiles. Le diagramme de stabilité montre le couple que vous devez appliquer au yacht pour l'incliner à un certain angle.
   
   
   
   

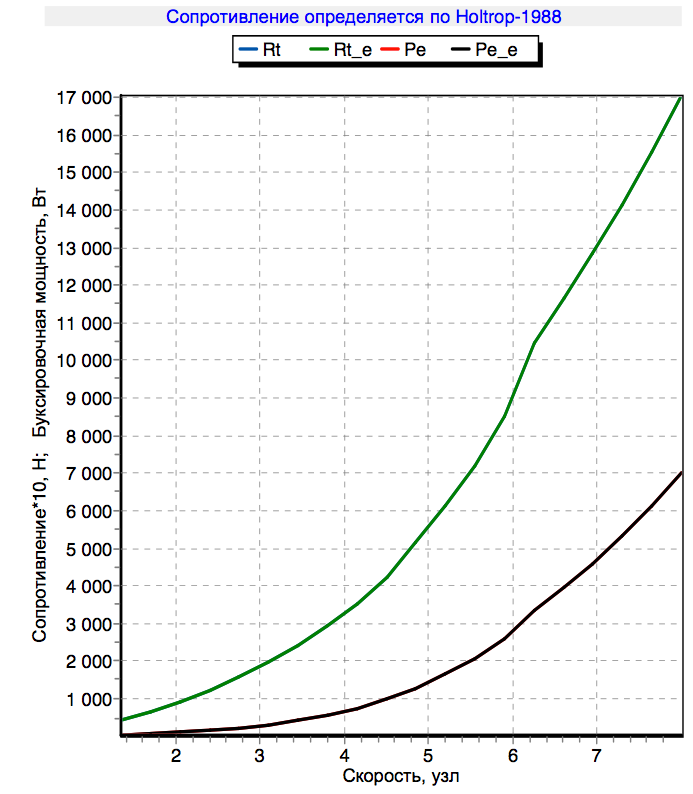
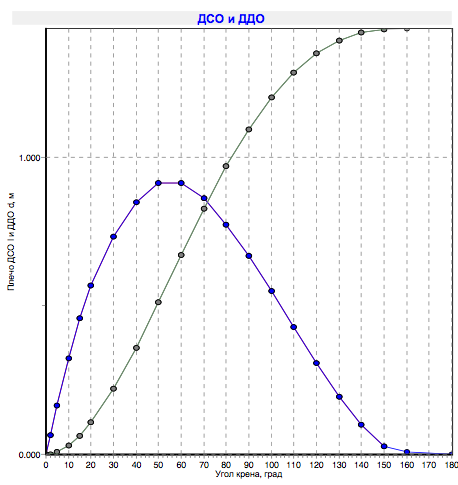
   Tous les arguments nécessaires sont rassemblés, procédons aux calculs.

   
   De toute évidence, en avançant, le yacht surmonte la force de résistance du vent de face. La vitesse du vent de face est égale à la vitesse du yacht, mais est dirigée dans la direction opposée. J'ai déjà utilisé cette analogie lors du choix d'un moteur .
   

   $$

   $$R_ {fw} = 0,61 * S_ {fr} * v ^ 2, H,$$
   
   où v est la vitesse du navire.
   
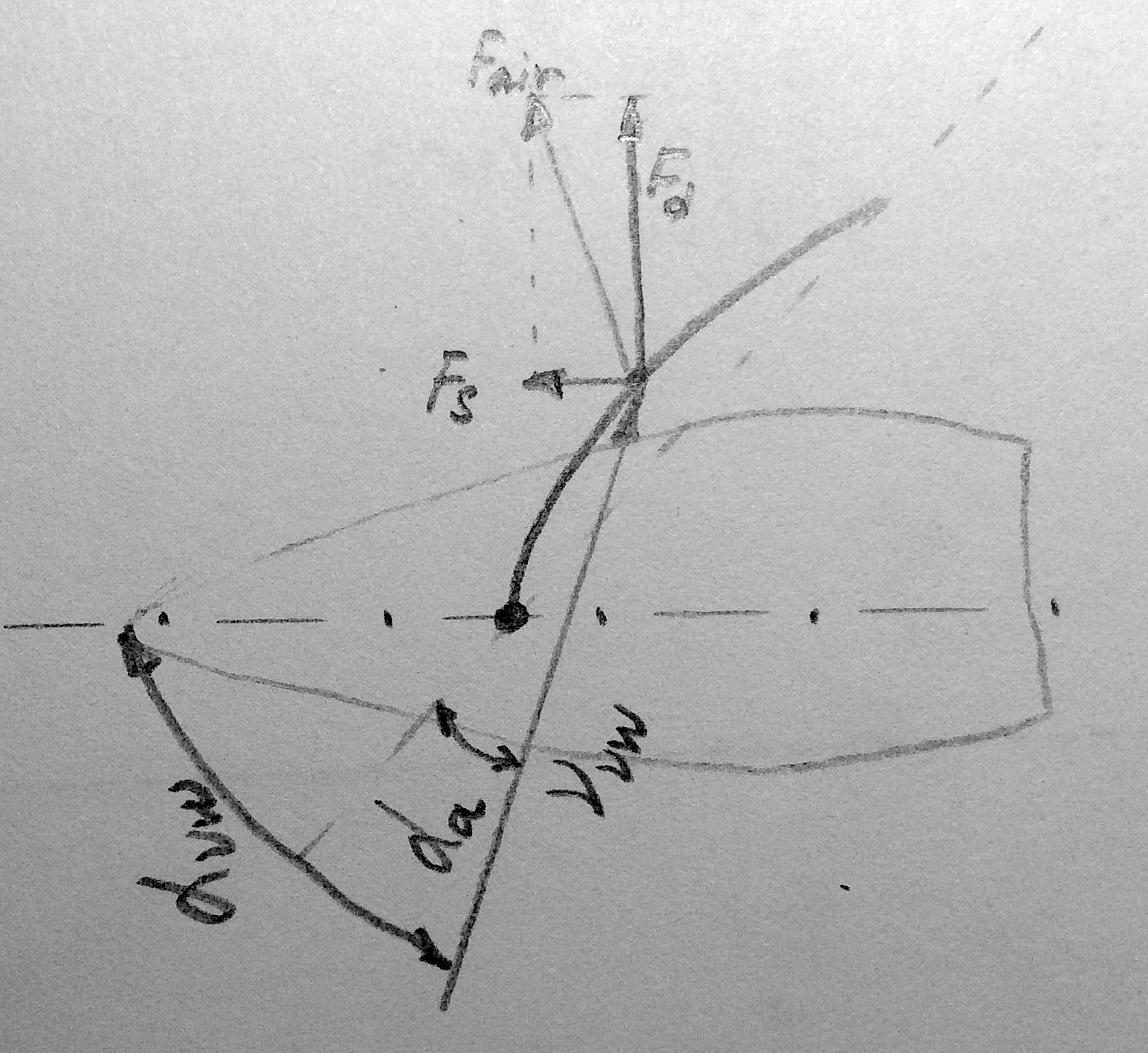
   Dans le même temps, la force du vent réel agit sur le yacht $$$F_ {rw}$ soufflant à un certain angle $$$\ alpha_ {rw}$ . Ces deux vents créent une force égale à la somme vectorielle des forces partielles. La soi-disant force du vent fanion - le vent qui souffle à bord du navire.
   
   Le problème principal est la théorie de la relativité. L'observateur (et tous les instruments de mesure) est à bord du yacht et pour lui, il n'y a aucun moyen de mesurer la force et la direction du vent réel, mais il peut mesurer la direction - $$$\ alpha_ {vw}$ et la vitesse du vent fanion - $$$v_ {vw}$ ainsi que la direction - $$$\ alpha$ mesuré par une boussole embarquée et la vitesse du navire - $$$v$ mesuré par un décalage à bord (compteur de vitesse).
   
   Je trouve les paramètres réels du vent basés sur des mesures d'instruments embarqués.
   $$$v_ {rw} = \ sqrt {v ^ 2 + v_ {vw} ^ 2-2 * v * v_ {vw} * cos (\ alpha_ {vw})}$ - vitesse du vent réel;
   $$$\ alpha_ {rw} = \ pi-arccos (\ frac {v_ {rw} ^ 2 + v ^ 2-v_ {vw} ^ 2} {2 * v * v_ {rw}})$ - l'angle du vent réel reporté de la direction "avant".
   
   
   
   Pour les petits pokatushek, tout cela n'a pas de sens. La connexion entre le vent réel et le fanion est nécessaire pour planifier des voyages suffisamment longs (lorsque la cible n'est pas en ligne de vue directe). Après tout, la planification est effectuée sur une carte de la planète avec l'indication des vents réels (selon les prévisions météorologiques), et le mouvement du yacht provient d'un vent fanion.
   
   Maintenant que le lien avec la réalité a été établi, il est temps de comprendre comment la force motrice naît. Il est clair que le vent remplit les voiles et que le bateau longe les vagues.
   
   En fait, une voile sur un yacht fonctionne selon deux modes principaux:
   
   
   1. mode d'aile aérodynamique - utilisé par vent de face,
      
   2. mode de freinage aérodynamique - utilisé par vent fort.
      
   
   Le profil de la voile est cousu de telle sorte que, étant rempli d'un vent de face, il prend la forme d'une aile. Autrement dit, il y a une aile se déplaçant à une certaine vitesse par rapport à l'air - par conséquent, une force de levage se produit en elle $$$F_ {air}$ . Par analogie avec l'aile d'un avion, je vais essayer de simplifier sa taille et sa direction par rapport au yacht.
   
   Pour que la voile prenne sa forme de travail, il faut la tourner un peu par rapport à la direction du vent. L'angle de rotation est appelé "angle d'attaque" $$$\ alpha_ {a}$ . Pour simplifier les calculs, l'aile est comparée à une plaque plate et les différences sont présentées sous la forme d'un tableau de coefficients aérodynamiques , où Su est le coefficient de différence de portance et Cx est le coefficient de différence de résistance. La force de levage est dirigée perpendiculairement à la plaque et la force de résistance est parallèle. La géométrie de la plaque est déterminée par le coefficient d'élongation aérodynamique $$$A_ {y} = h ^ 2 / S$ où h est la hauteur de la voile; S est la zone de la voile.
   
   

   mais	Cy; Ay = 6	Cx	Cy; Ay = 3	Cx
   0	0	0,09	0	0,09
   5	0,83	0,1	0,65	0,1
   10	1.19	0,15	0,9	0,15
   15	1,22	0,3	1,1	0,25
   20	1,14	0,4	1.18	0,4
   25	1.06	0,485	1,2	0,5
   30	0,98	0,57	1	0,55
   40	0,9	0,73	0,82	0,65
   45	0,75	0,88	0,7	0,85
   50	0,6	1	0,6	1
   70	0,2	1,15	0,2	1,15
   90	0	1,2	0	1,2

   
   L'aile, contrairement à la plaque, est une structure tridimensionnelle, donc un tableau séparé montre comment la taille du renflement du "ventre" affecte les coefficients de différence par rapport à la plaque.
   

   ventre	Su3	Cx3
   0,0667	-0,2	0,1
   0,1	0	0
   0,2	0	0,1
   0,25	0,1	0,2

   
   Projection de la force de voile $$$F_ {air}$ à la direction longitudinale du yacht - puissance utile:
   $$$F_ {s} = 0,61 * v_ {vw} ^ 2 * S * ((Cy + Cy3) * sin (\ alpha_ {vw}) - (Cx + Cx3) * cos (\ alpha_ {vw}))$ .
   Projection de la force de voile $$$F_ {air}$ sur la direction transversale du yacht - force de dérive:
   $$$F_ {d} = 0,61 * v_ {vw} ^ 2 * S * ((Cy + Cy3) * cos (\ alpha_ {vw}) - (Cx + Cx3) * sin (\ alpha_ {vw}))$ .
   
   La force de la résistance au vent de la coque ralentira le mouvement:
   $$$R_ {fw} = 0,61 * S_ {fr} * v_ {vw} ^ 2 * sin (\ alpha_ {vw})$
   Ayant reçu la projection des forces, je peux trouver les vecteurs de vitesse longitudinale et transversale du yacht. Composante longitudinale de la vitesse $$$v_ {dp}$ Je trouve la caractéristique de remorquage selon le planning.
   Avec la composante transversale, tout est plus compliqué.
   Vous devez d'abord trouver la hauteur du centre de la voile. Une voile est un triangle dont un côté est un arc convexe. Je vais la présenter comme deux voiles: une pièce triangulaire et une en forme de faucille. L'aire du triangle est calculée comme la moitié du produit de la largeur par la hauteur, et l'aire de la "faucille" est la différence entre l'aire de la voile et l'aire du triangle.
   

   $$

   $$S = (h_ {gr top} -h_ {gr hls}) * l_ {gr sht} / 2,$$
   où $$$S_ {faucille} = S_ {gr} -S$
   Hauteur du centre de la voile:
   

   $$

   $$h_ {gr cp} = \ frac {h_ {gr \ Delta cp} * S \ Delta + ((h_ {gr top} -h_ {gr pc}) * S_ {faucille} / 1,8)} {S_ {gr }},$$
   où $$$h_ {gr \ Delta cp} = h_ {gr pc} + (h_ {gr top} + h_ {gr hl} -2 * h_ {gr pc}) / 3,$ la hauteur du centre de la voile voile triangle sans faucille.
   Habituellement, un yacht a deux voiles: le principal est la grand-voile et l'avant est la trinquette. La trinquette est généralement réalisée sans faucille puis sa hauteur au centre de la voile:
   

   $$

   $$h_ {st \ Delta cp} = h_ {st st} + (h_ {st top} + h_ {st hls} -2 * h_ {st sht}) / 3$$
   
   Total Sailing Center:
   

   $$

   $$h _ {\ Sigma cpu} = \ frac {h_ {gr cp} * S_ {gr} + h_ {ct \ Delta cp} * S_ {ct}} {S_ {gr} + S_ {ct}}$$
   
   Maintenant, je peux déterminer le moment d'inclinaison agissant sur le yacht:
   

   $$

   $$M_ {kr} = F_ {d} * h _ {\ Sigma cp}.$$
   
   Du diagramme de stabilité je trouve l'angle du yacht $$$\ phi$ .
   J'exprime la force de la dérive du yacht:
   

   $$

   $$R_ {d} = 9,8 * 102 * (S_ {ks} * atan (\ frac {v_ {d}} {v_ {dp}}) * v_ {dp} ^ 2 * (cos (\ phi- \ gamma) -cos (\ phi + \ gamma)) * 0,96+ (S_ {ks} + S_ {dp w}) * 1,15 * v_ {d} ^ 2 * cos (\ phi- \ gamma)),$$
   où est l'angle des quilles du yacht à deux quilles par rapport à la verticale.
   La force de la pression du vent sur le corps donne une dérive supplémentaire.
   

   $$

   $$F_ {anf} = 0,61 * v_ {d} ^ 2 * S_ {anf} * cos (\ alpha_ {vw}).$$
   
   La vitesse $$$v_ {d}$ est une substitution de demi-division jusqu'à un équilibre des forces $$$F_ {d} + F_ {anf} = R_ {d}$ .
   Maintenant, il est évident que le yacht se déplace «obliquement», c.-à-d. a une vitesse de déplacement transversale et longitudinale. Cela apporte une autre surprise. Direction - $$$\ alpha$ mesuré par une boussole embarquée et la vitesse du navire - $$$v = v_ {dp}$ mesurées par le décalage à bord (compteur de vitesse) ne montrent que la composante longitudinale.
   Il est nécessaire d'attacher des dimensions à la réalité. L'angle réel du navire $$$\ alpha_ {real}$ appelé "angle de voie":
   

   $$

   $$\ alpha_ {real} = atan (\ frac {v_ {d}} {v_ {dp}}) + \ alpha$$
   
   et peut différer de la mesure de 10-20 degrés.
   La vitesse réelle du yacht peut être déterminée par le théorème de Pythagore:
   

   $$

   $$v_ {real} = \ sqrt {v_ {dp} ^ 2 + v_ {d} ^ 2}.$$
   
   
   En conclusion, je vais donner un exemple de calcul pour mon bateau la situation la plus intéressante - le mouvement contre le vent. Il est clair que vous ne vous opposerez pas strictement au vent sous les voiles, mais à un certain angle, vous pouvez.
   
   Vous devez commencer par la voile avant - la trinquette est montée sur le haut du mât, l'angle avant de la proue du yacht et l'arrière avec une feuille (câble souple) à travers le rouleau jusqu'au treuil. Sa tension régule l'angle de la voile par rapport au yacht. Angle d'installation minimum $$$\ psi_ {st min} = 18 ^ o$ obtenu à la tension maximale de la feuille. Extension aérodynamique de la trinquette $$$A_ {y st} = h_ {st} ^ 2 / S_ {st} = 5,8$ . En utilisant la méthode d'interpolation linéaire, je trouve l'angle d'attaque optimal $$$\ alpha_ {a} = 10 ^ o$ du tableau des coefficients aérodynamiques. Critère d'optimalité - Maximisation $$$F_ {s st}$ où Su = 1,17; Cx = 0,15. La trinquette installée de cette façon fonctionnera efficacement dans la direction du vent fanion $$$\ alpha_ {vw} = \ psi_ {ct} + \ alpha_ {a} = 18 + 10 = 28 ^ o$ . Bon temps de navigation à pied lorsque la vitesse du vent est d'environ 5-7 m / s. Pour la beauté des chiffres, je prendrai $$$v_ {vw} = 6,55 m / s$ .
   
   La projection de la force de la trinquette sur la direction longitudinale du yacht est une force utile:
   

   $$

   $$F_ {s st} = 0,61 * 6,55 ^ 2 * 14 * ((1,17 + 0) * sin (28 * \ pi / 180) - (0,15 + 0) * cos (28 * \ pi / 180)) = 153,5 H$$
   
   La projection de la force de la trinquette sur la direction transversale du yacht - la force de dérive:
   

   $$

   $$F_ {d st} = 0,61 * 6,55 ^ 2 * 14 * ((1,17 + 0) * cos (28 * \ pi / 180) - (0,15 + 0) * sin (28 * \ pi / 180)) = 405,8 H$$
   
   La résistance au vent de la coque empêche le mouvement vers l'avant.
   

   $$

   $$R_ {fr w} = 0,61 * 6,55 ^ 2 * 3 * cos (28 * \ pi / 180) = 69 H$$
   
   Selon la caractéristique de remorquage, nous déterminons la vitesse $$$v_ {dp} = 2,75$ nœud = 1,4 m / s
   

   $$

   $$h_ {st \ Delta cp} = 1,5 + (10 + 1,5-2 * 1,1) / 3 = 4,6 m$$
   
   $$$M_ {kr st} = 405,8 * 4,6 = 1867 N / m$ , à partir du diagramme de stabilité, nous trouvons l'angle de talon $$$\ phi_ {ct} = 3,9 ^ o$ . Eh bien, ce sont des bagatelles, donc nous ajouterons une voile de plus - la grand-voile!
   La grand-voile fonctionne comme un volet sur l'aile d'un avion et tourne autour du mât à un angle $$ . Le coefficient d'allongement aérodynamique de la grand-voile $$$A_ {y gr} = h_ {gr} ^ 2 / S_ {gr} = 4,9$ ;
   angle d'attaque optimal $$$\ alpha_ {a} = 10 ^ o$ ; Su = 1,09; Cx = 0,15.
   La projection de la force de la grotte sur la direction longitudinale du yacht est une force utile:
   

   $$

   $$F_ {s gr} = 0,61 * 6,55 ^ 2 * 17,2 * ((1,09 + 0) * sin (28 * \ pi / 180) - (0,15 + 0) * cos ( 28 * \ pi / 180)) = 170 H$$
   
   La projection de la force de la grotte sur la direction transversale du yacht est la force de dérive:
   

   $$

   $$F_ {d gr} = 0,61 * 6,55 ^ 2 * 17,2 * ((1,09 + 0) * cos (28 * \ pi / 180) - (0,15 + 0) * sin ( 28 * \ pi / 180))) = 464 H$$
   
   $$$h _ {\ Sigma cpu} = 4,16 m$ , $$$M_ {kr} = 3127 H$ et angle de roulis $$$\ phi _ {\ Sigma} = 8.5 ^ o$ .
   Force avant totale:
   $$$F_ {s} = F_ {s st} + F_ {s gr} -R_ {fr w} = 153,5 + 170-69 = 254 H$ vitesse d'avancement $$$v_ {dp} = 3,6$ nœud ou 1,86 m / s.
   Si nous supposons que le vent réel souffle strictement vers le nord, la boussole à bord montrera l'angle de la composante longitudinale de la vitesse du yacht $$$\ alpha_ {vw} = 38,1 ^ o$ .
   La vitesse de dérive sera $$$v_ {d} = 0,418 m / s$ .
   Maintenant, nous devons concrétiser ces résultats.
   
   L'angle de trajectoire du mouvement réel sera:
   $$$\ alpha_ {real} = atan (\ frac {v_ {d}} {v_ {dp}}) + \ alpha = atan (\ frac {0.418} {1.86}) + 38.1 = 51 ^ o$ , c'est l'angle du vent réel $$$\ alpha_ {rw}$ au vecteur de mouvement du yacht.
   
   Et la vraie vitesse de déplacement dans l'espace: $$$v_ {real} = \ sqrt {v_ {dp} ^ 2 + v_ {d} ^ 2}$ = 1,92 + 0,4182 = 1,9 m / s.
   Vitesse du vent réel:
   $$$v_ {rw} = \ sqrt {v ^ 2 + v_ {vw} ^ 2-2 * v * v_ {vw} * cos (\ alpha_ {vw})} = 5 m / s$ .
   Dans de telles conditions, la vitesse d'avance strictement contre le vent sera de 1,2 m / s ou 2,35 nœuds, et vous devrez vous déplacer le long d'un chemin en zigzag - pointes.
   
   Après avoir calculé d'autres angles possibles du vent fanion, vous pouvez obtenir un diagramme de virement circulaire de la dépendance de la vitesse réelle du yacht par rapport au vent réel. 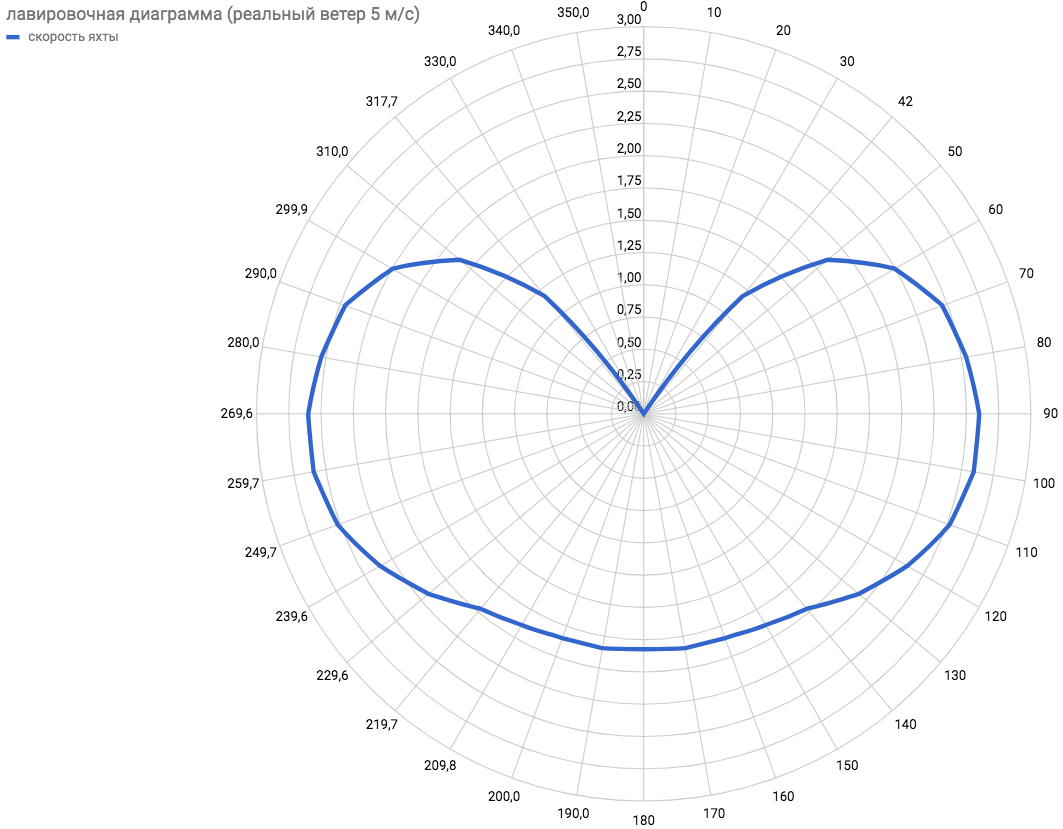En l'utilisant, vous pouvez déjà planifier des itinéraires sur la carte en fonction des prévisions de vent. En outre, il est devenu clair que l'angle minimal possible $$$\ alpha_ {real min} = 43,5 ^ o$ , et la vitesse maximale contre le vent est atteinte avec l'angle de cap $$ pour vent 5 m / s.