Traduction d'une longue lecture intéressante consacrée à la visualisation de concepts issus de la théorie de l'information. Dans la première partie, nous verrons comment représenter graphiquement les distributions de probabilité, leur interaction et les probabilités conditionnelles. Ensuite, nous traiterons des codes de longueur fixe et variable, verrons comment le code optimal est construit et pourquoi il en est ainsi. En complément, le paradoxe statistique Simpson est visuellement compris.La théorie de l'information nous donne un langage précis pour décrire beaucoup de choses. Quelle est l'incertitude en moi? Quelle connaissance de la réponse à la question A me dit sur la réponse à la question B? Dans quelle mesure un ensemble de croyances est-il similaire à un autre? J'avais des versions informelles de ces idées quand j'étais enfant, mais la théorie de l'information les cristallise en idées précises et puissantes. Ces idées ont une grande variété d'applications, de la compression de données à la physique quantique, à l'apprentissage automatique et aux vastes domaines qui les séparent.
Malheureusement, la théorie de l'information peut sembler intimidante. Je ne pense pas qu'il y ait de raison à cela. En fait, de nombreuses idées clés peuvent être expliquées visuellement!
Visualisation de la distribution des probabilités
Avant de nous plonger dans la théorie de l'information, réfléchissons à la façon dont vous pouvez visualiser des distributions de probabilité simples. Nous en aurons besoin plus tard, de plus, ces techniques de visualisation des probabilités sont utiles en elles-mêmes!
Je suis en Californie. Parfois il pleut, mais surtout le soleil! Disons, 75% du temps, il fait beau. Il est facile à représenter sur l'image:
La plupart du temps, je porte un T-shirt, mais parfois je porte un imperméable. Supposons que je porte un imperméable 38% du temps. C'est aussi facile à représenter.
Et si je veux visualiser les deux faits en même temps? C'est simple s'ils n'interagissent pas - c'est-à-dire sont indépendants. Par exemple, si ça: que je porte un T-shirt ou un imperméable aujourd'hui ne dépend pas de la météo la semaine prochaine. Nous pouvons illustrer cela en utilisant un axe pour une variable et un pour l'autre:
Faites attention aux lignes droites verticales et horizontales qui traversent. Voilà à quoi ressemble l'indépendance! La probabilité que je porte un imperméable ne changera pas car il pleuvra dans une semaine. En d'autres termes, la probabilité que je porte un imperméable et qu'il pleuve la semaine prochaine est égale à la probabilité que je porte un imperméable multipliée par la probabilité qu'il pleuve. Ils n'interagissent pas.
Lorsque les variables interagissent, la probabilité peut augmenter pour certaines paires de variables et diminuer pour d'autres. Il y a une forte probabilité que je porte un imperméable et il pleut parce que les variables sont corrélées, elles se rendent plus probables. Il est plus probable que je porte un imperméable un jour où il pleut que la probabilité que je porte un imperméable un jour et qu'il pleuve un autre jour au hasard.
Visuellement, il semble que certains des carrés gonflent avec une probabilité supplémentaire, tandis que les autres carrés se rétrécissent, car il est peu probable que deux événements se produisent simultanément:
Mais même si ça a l'air cool, ce n'est pas très utile pour comprendre ce qui se passe.
Au lieu de cela, concentrons-nous sur une variable comme la météo. Nous connaissons les probabilités de temps ensoleillé et pluvieux. Dans les deux cas, nous pouvons considérer les probabilités conditionnelles. Quelle est la probabilité que je porte un T-shirt s'il fait beau? Quelle est la probabilité que je porte un imperméable s'il pleut?
Avec une probabilité de 25%, il pleuvra. S'il pleut, je porterai un imperméable avec 75% de chances. Ainsi, la probabilité qu'il pleuve et que je porte un imperméable est de 25% à 75%, soit environ 19%. La probabilité qu'il pleuve et que je porte un imperméable est la probabilité qu'il pleuve multipliée par la probabilité que je porte un imperméable s'il pleut. Nous l'écrivons comme ceci:
Voici un exemple de l'une des identités les plus fondamentales de la théorie des probabilités:
Nous factorisons la distribution en la divisant en un produit en deux parties. Tout d'abord, nous examinons la probabilité qu'une variable, la météo, prenne une certaine valeur. Ensuite, nous examinons la probabilité qu'une autre variable, mes vêtements, prenne la valeur due à la première variable.
La variable de départ n'a pas d'importance. Nous pourrions commencer par mes vêtements, puis regarder la météo causée par cela. Cela peut sembler moins intuitif car on comprend qu'il existe une relation causale entre la météo qui affecte ce que je porte et non l'inverse ... mais ça marche quand même!
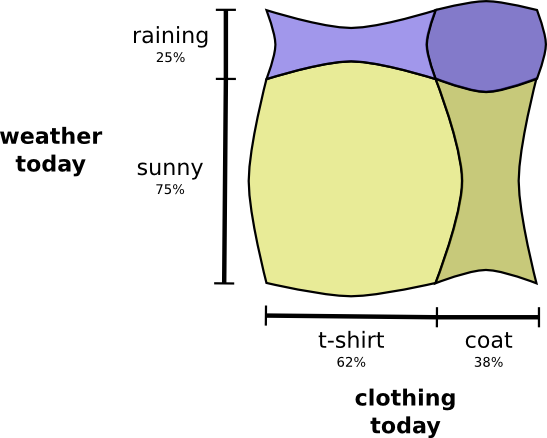
Regardons un exemple. Si nous choisissons un jour au hasard, avec une probabilité de 38%, je porterai un imperméable. Si nous savons que je porte un imperméable, quelle est la probabilité qu'il pleuve? Je préfère porter un imperméable sous la pluie qu'au soleil, mais la pluie en Californie est rare, et il s'avère qu'avec 50% de chances, il pleuvra. Donc, la probabilité qu'il pleuve et que je porte un imperméable est la probabilité que je porte un imperméable (38%), multipliée par la probabilité qu'il pleuve si je porte un imperméable (50%), ce qui est environ 19%.
Cela nous donne une deuxième façon de visualiser la même distribution de probabilité.
Veuillez noter que les valeurs des étiquettes ont une signification légèrement différente de celle du schéma précédent: un t-shirt et un imperméable sont désormais les probabilités limites, la probabilité que je porte ces vêtements sans tenir compte de la météo. D'un autre côté, il y a maintenant deux marques de pluie et de soleil, car leurs probabilités dépendent du fait que je porterai un T-shirt ou un imperméable.
(Vous avez peut-être entendu parler du théorème de Bayes. Vous pouvez l'imaginer comme un moyen de transition entre ces deux façons différentes de représenter la distribution de probabilité!)
Encadré: Le paradoxe de Simpson
Ces techniques de visualisation des distributions de probabilité sont-elles vraiment utiles? Je pense que oui! Un peu plus loin, nous les utilisons pour visualiser la théorie de l'information, mais pour l'instant nous les utilisons pour étudier le paradoxe Simpson. Le paradoxe de Simpson est une situation statistique extrêmement peu intuitive. Il est difficile de comprendre à un niveau intuitif. Michael Nielsen a écrit un excellent essai
Reinventing Explanation , qui explique le paradoxe à bien des égards. Je veux essayer de le faire moi-même, en utilisant les techniques que nous avons développées dans la section précédente.
Deux méthodes de traitement des calculs rénaux sont à l'essai. La moitié des patients reçoivent le traitement A, tandis que l'autre moitié reçoit le traitement B. Les patients qui ont reçu le traitement B étaient plus susceptibles de récupérer que ceux qui ont reçu le traitement A.
Cependant, les patients avec de petits calculs rénaux étaient plus susceptibles de récupérer s'ils recevaient un traitement A. Les patients avec de gros calculs rénaux dans le rein étaient également plus susceptibles de récupérer s'ils recevaient le traitement A! Comment est-ce possible?
L'essence du problème est que l'étude n'a pas été correctement randomisée. Parmi les patients recevant le traitement A, il y avait plus de patients avec de gros calculs rénaux et parmi les patients recevant le traitement B, il y en avait plus avec de petits calculs rénaux.
Il s'avère que les patients atteints de petits calculs rénaux sont beaucoup plus susceptibles de récupérer en général.
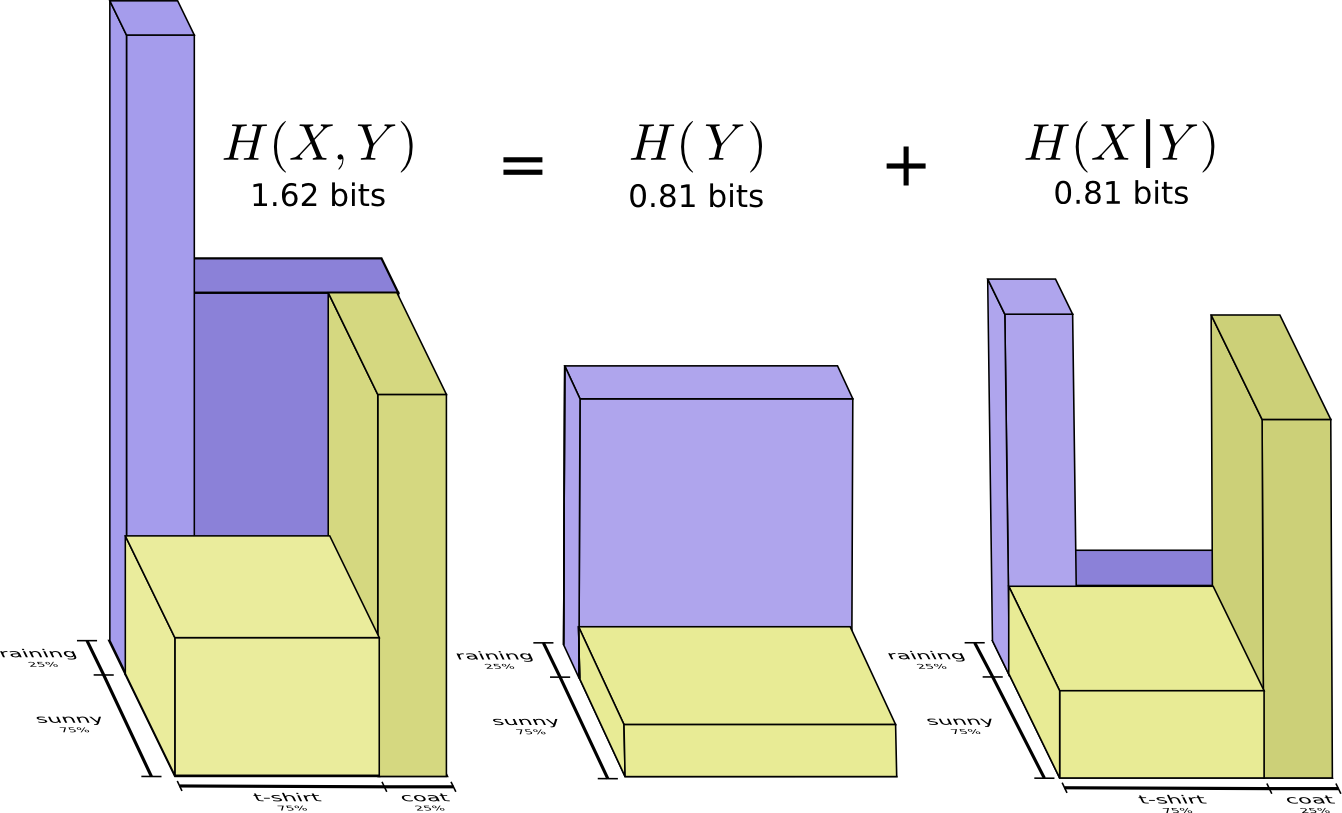
Pour mieux comprendre cela, nous pouvons combiner les deux schémas précédents. Le résultat est un graphique en trois dimensions avec un taux de récupération divisé en petits et gros calculs rénaux.
Maintenant, nous voyons que dans le cas des petites et des grosses pierres, le traitement A est supérieur au traitement B. Le traitement B ne semblait meilleur que parce que les patients auxquels il était appliqué avaient, en général, plus de chances de se rétablir!
Les codes
Maintenant que nous avons des moyens de visualiser la probabilité, nous pouvons plonger dans la théorie de l'information.
Permettez-moi de vous parler de mon ami imaginaire, Bob. Bob aime beaucoup les animaux. Il parle constamment des animaux. En fait, il ne parle que quatre mots: «chien», «chat», «poisson» et «oiseau».
Il y a quelques semaines, malgré le fait que Bob était le fruit de mon imagination, il a déménagé en Australie. De plus, il a décidé qu'il ne voulait communiquer qu'en format binaire. Tous mes messages (imaginaires) de Bob ressemblent à ceci:
Pour communiquer, Bob et moi devons créer un système de codage - un moyen d'afficher les mots dans une séquence de bits.
Pour envoyer un message, Bob remplace chaque caractère (mot) par le mot de code correspondant, puis les combine pour former une chaîne codée.
Codes de longueur variable
Malheureusement, les services de communication dans l'Australie imaginaire sont chers. Je dois payer 5 $ pour un peu de chaque message que je reçois de Bob. Ai-je mentionné que Bob aime beaucoup parler? Afin de ne pas faire faillite, Bob et moi avons décidé de découvrir s'il était possible de réduire d'une manière ou d'une autre la longueur moyenne des messages.
Il s'avère que Bob ne prononce pas tous les mots également souvent. Bob aime beaucoup les chiens. Il parle tout le temps de chiens. Parfois, il parle d'autres animaux - en particulier d'un chat que son chien aime chasser - mais surtout il parle de chiens. Voici un graphique de la fréquence de ses mots:
C'est encourageant. Notre ancien code utilise des mots de code 2 bits, quelle que soit leur fréquence d'utilisation.
Il existe un bon moyen de visualiser cela. Dans le diagramme suivant, nous utilisons l'axe vertical pour visualiser la probabilité de chaque mot
et un axe horizontal pour visualiser la longueur du mot de code correspondant
. Veuillez noter que la zone résultante est la longueur moyenne du mot de code que nous envoyons, dans ce cas 2 bits.
Nous pouvons être plus intelligents et rendre la longueur du code variable, où les mots de code pour les mots communs sont raccourcis. Le problème est qu'il y a une concurrence entre les mots de code - en raccourcissant certains, nous sommes obligés de rallonger d'autres. Pour minimiser la longueur du message, idéalement, nous aimerions que tous les mots de code soient courts, mais le plus court devrait être largement utilisé. Ainsi, le code résultant contient des mots de code plus courts pour les mots courants (par exemple, «chien») et des mots de code plus longs pour les mots rares (par exemple, «oiseau»).
Visualisons à nouveau cela. Veuillez noter que les mots de code les plus courants sont plus courts et les plus rares sont plus longs. En conséquence, nous avons obtenu une zone plus petite. Cela correspond à une longueur de mot de code attendue plus courte. La longueur moyenne des mots de code est maintenant de 1,75 bits!
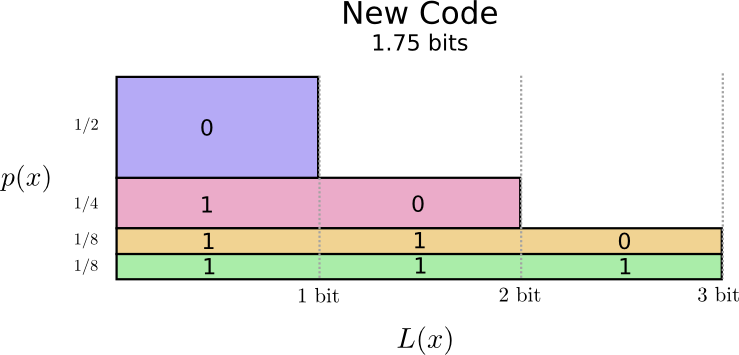
(Vous vous demandez peut-être: pourquoi ne pas utiliser 1 séparément comme mot de code? Malheureusement, cela entraînera une ambiguïté lors du décodage des chaînes codées. Nous en reparlerons un peu plus tard.)
Il s'avère que ce code est le meilleur possible. Il n'y a pas de code pour cette distribution qui nous donnerait une longueur moyenne de mot de code inférieure à 1,75 bits.
Il y a une limite fondamentale. La transmission de ce mot a été dit, quel événement de cette distribution s'est produit, nous oblige à transmettre une moyenne d'au moins 1,75 bits. Quel que soit le degré d'intelligence de notre code, il est impossible d'obtenir une longueur de message moyenne inférieure. Nous appelons cette limite fondamentale l'
entropie de distribution - nous en discuterons plus en détail ci-dessous.
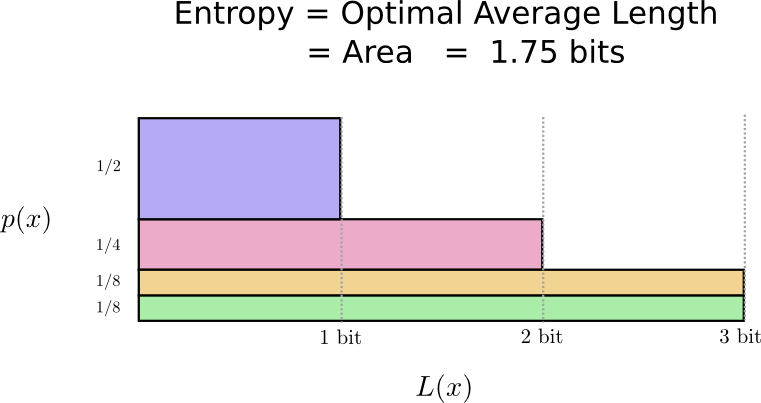
Si nous voulons comprendre cette limite, nous devons comprendre le compromis entre garder certains mots de code courts et d'autres longs. Une fois que nous avons compris cela, nous pouvons comprendre à quoi ressemblent les meilleurs systèmes de codage possibles.
Espace de mot de code
Il y a deux mots de code d'une longueur de 1 bit: 0 et 1. Il y a quatre mots de code d'une longueur de 2 bits: 00, 01, 10 et 11. Chaque bit que vous ajoutez double le nombre de mots de code possibles.
Nous nous intéressons aux codes de longueur variable, où certains mots de code sont plus longs que d'autres. Nous pouvons avoir des situations simples lorsque nous avons huit mots de code de 3 bits. Il peut y avoir des mélanges plus complexes, par exemple, deux mots de code de longueur 2 et quatre mots de code de longueur 3. Qu'est-ce qui décide du nombre de mots de code de longueurs différentes que nous pouvons avoir?
Rappelez-vous que Bob transforme ses messages en chaînes cryptées, remplaçant chaque mot par son code et les concaténant.
Il y a une question subtile à être prudent lors de la création de codes de longueur variable. Comment diviser la chaîne codée en mots de code? Lorsque tous les mots de code ont la même longueur, c'est facile - il suffit de diviser la chaîne en morceaux de cette longueur. Mais comme il existe des mots de code de différentes longueurs, nous devons faire attention au contenu.
Nous voulons que notre code soit uniquement décodable. Et nous ne voulons pas qu'il soit ambigu pour déterminer quels mots de code composent la chaîne codée. Si nous avions un symbole spécial «fin du mot de code», ce serait simple. Mais nous n'en avons pas - nous n'envoyons que 0 et 1. Nous devons être en mesure de regarder la séquence de mots de code et de déterminer où se termine chacun d'eux.
Il est très simple de créer des codes qui ne peuvent pas être décryptés sans ambiguïté. Par exemple, imaginez que 0 et 01 sont tous deux des mots de code. Ensuite, on ne sait pas quel est le premier mot de code de la ligne 0100111 - ce peut être ceci ou cela! La propriété dont nous avons besoin est que si nous voyons un mot de code spécifique, il ne doit pas être inclus dans un autre mot de code plus long. En d'autres termes, aucun mot de code ne doit être le préfixe d'un autre mot de code. C'est ce qu'on appelle une propriété de préfixe, et les codes qui lui obéissent sont appelés
codes de préfixe .
Une façon utile de représenter cela est que chaque mot de code nécessite des sacrifices de l'espace des mots de code possibles. Si nous prenons le mot de code 01, nous perdons la possibilité d'utiliser les mots de code dont il est le préfixe. Nous ne pouvons plus utiliser 010 ou 011010110 en raison de l'ambiguïté - ils nous sont perdus.
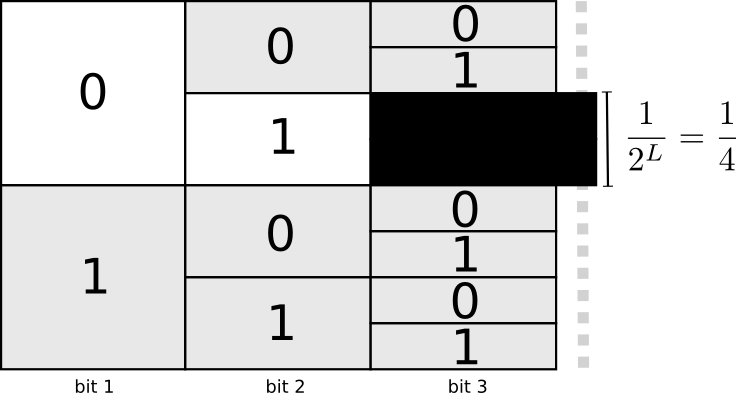
Étant donné qu'un quart de tous les mots de code commence à 01, nous avons fait don d'un quart de tous les mots de code possibles. Voici le prix que nous payons en échange du fait que nous avons un mot de code d'une longueur de seulement 2 bits! À son tour, ce sacrifice signifie que tous les autres mots de code devraient être légèrement plus longs. Il y a toujours une sorte de compromis entre les longueurs des différents mots de code. Un mot de code court vous oblige à sacrifier la majeure partie de l'espace des mots de code possibles, ce qui empêche la brièveté des autres mots de code. Ce que nous devons découvrir, c'est comment faire des compromis correctement!
Codage optimal
Vous pouvez le considérer comme un budget limité que vous pouvez dépenser pour obtenir des mots de code courts. Nous payons pour un mot de code, en sacrifiant une partie des mots de code possibles.
Le coût d'achat d'un mot de code de longueur 0 est de 1 - tous les mots de code possibles - si vous voulez avoir un mot de code de longueur 0, vous ne pouvez pas avoir d'autre mot de code. Le coût d'un mot de code d'une longueur de 1, par exemple, «0», est de 1/2, car la moitié des mots de code possibles commencent par «0». Le coût d'un mot de code de longueur 2, par exemple «01», est de 1/4, car un quart de tous les mots de code possibles commence par «01». En général, le coût des mots de code diminue de façon exponentielle avec l'augmentation de la longueur du mot de code.
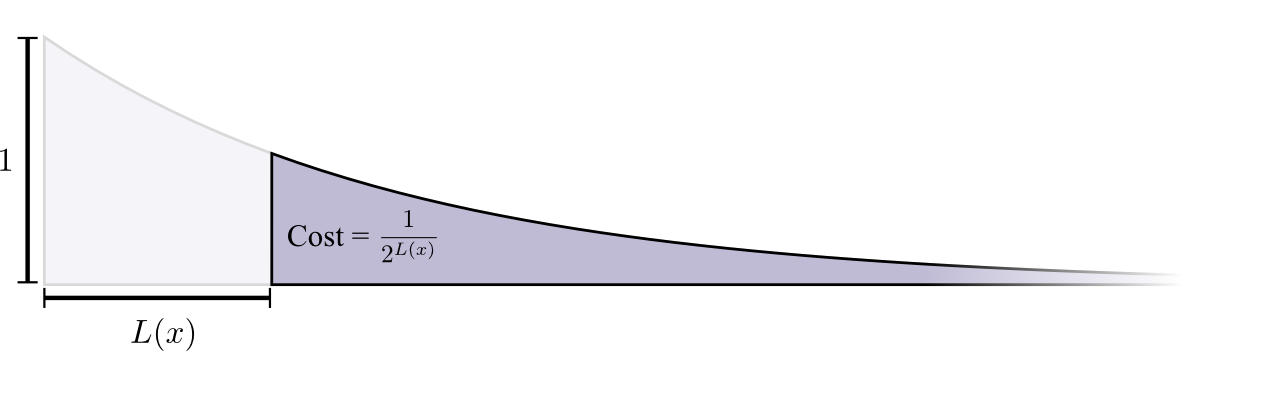
Veuillez noter que si le coût diminue en tant qu'exposant (en nature), c'est à la fois la hauteur et la surface! (
L'exemple utilise un exposant de base 2 où ce fait est incorrect, mais vous pouvez passer à l'exposant naturel, ce qui simplifie visuellement la preuve. )
Nous avons besoin de mots de code courts parce que nous voulons réduire la longueur moyenne des messages. Chaque mot de code augmente la longueur moyenne des messages de la probabilité que ce mot multiplie par sa longueur. Par exemple, si nous devons envoyer un mot de code de 4 bits dans 50% des cas, notre longueur moyenne de message sera 2 bits plus longue que si nous n'avions pas envoyé ce mot de code. Nous pouvons imaginer cela comme un rectangle.
Ces deux valeurs sont liées par la longueur du mot de code. Le prix que nous payons détermine la longueur du mot de code. La longueur du mot de code détermine combien il ajoute à la longueur moyenne du message. On peut les imaginer ensemble comme ça.
Les mots de code courts réduisent la longueur moyenne des messages, mais sont chers, tandis que les mots de code longs augmentent la longueur moyenne des messages, mais sont bon marché.
Quelle est la meilleure façon d'utiliser notre budget limité? Combien devrions-nous dépenser pour un mot de passe pour chaque événement?
Tout comme une personne souhaite investir davantage dans des outils qu'elle utilise régulièrement, nous voulons dépenser davantage pour les mots de code couramment utilisés. Il y a une façon particulièrement naturelle de le faire: répartir notre budget proportionnellement à la fréquence de l'événement. Donc, si un événement se produit dans 50% des cas, nous dépensons 50% de notre budget à l'achat d'un mot de code court pour celui-ci. Mais si l'événement ne se produit que 1% du temps, nous ne dépensons que 1% de notre budget, car nous ne sommes pas très inquiets sur la longueur du mot de code.
C'est une chose assez naturelle, mais est-elle optimale? Il en est ainsi, et je vais le prouver!
La preuve suivante est claire et doit être comprise, mais il faudra du travail pour la comprendre, et c'est certainement la partie la plus difficile de cet essai. Les lecteurs peuvent le sauter en toute sécurité, accepter le fait sans preuve et passer à la section suivante.Regardons un exemple spécifique où nous devons dire lequel des deux événements possibles s'est produit. Événement temps et l'événement se produit temps. Nous répartissons notre budget de la manière naturelle décrite ci-dessus, en dépensant notre budget de mots de passe courts et
pour recevoir un mot de code court .
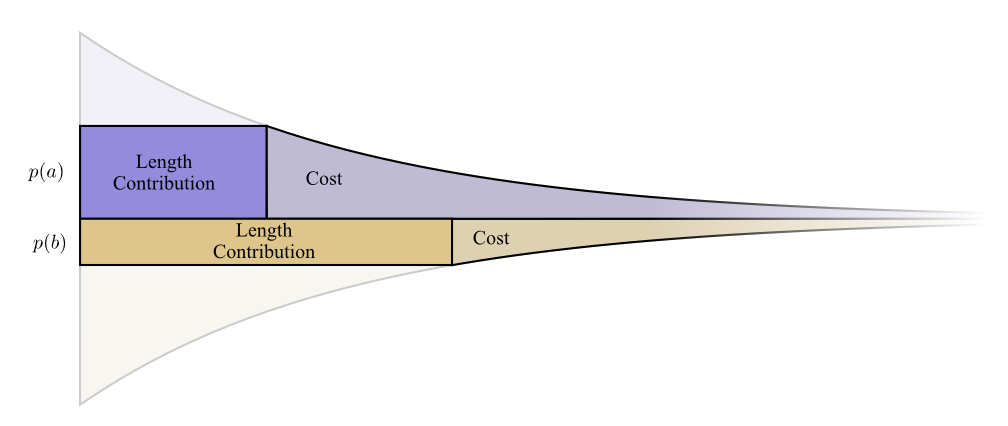Les limites du coût et de la longueur s'harmonisent à merveille. Est-ce que cela signifie quelque chose?Considérez ce qui arrive à la contribution du coût et de la longueur si nous modifions un peu la longueur du mot de code. Si nous augmentons légèrement la longueur du mot de code, alors la contribution de la longueur du message augmentera proportionnellement à sa hauteur à la frontière, et le coût diminuera proportionnellement à sa hauteur à la frontière.
Ainsi, le coût de création d'un mot de code plus court est .
Nous ne sommes pas également préoccupés par la longueur de chaque mot de code; ils nous intéressent proportionnellement à la fréquence à laquelle nous les utilisons. En cas de .
Notre gain en raccourcissant le mot de code est proportionnel .
Fait intéressant, les deux dérivés sont les mêmes. Cela signifie que notre budget initial a une caractéristique intéressante: si vous aviez un peu plus d'argent, il serait tout aussi bon d'investir dans la réduction de n'importe quel mot de code. Ce qui nous passionne vraiment, c'est le rapport avantages / coûts - c'est ce qui décide dans quoi nous devrions investir davantage. Dans ce cas, le rapport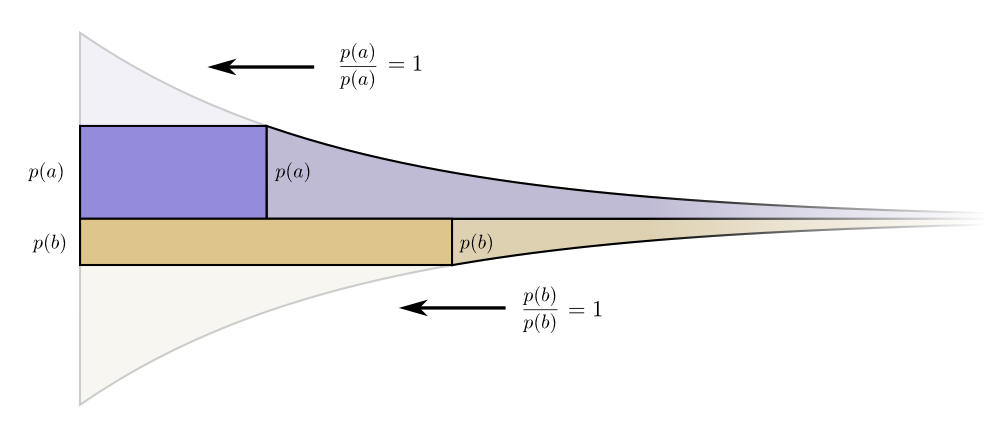
.
Il fait un mot de code pour .
Mais les avantages sont les mêmes. Cela conduit au fait que le rapport coût / bénéfice pour l'achat sera
.
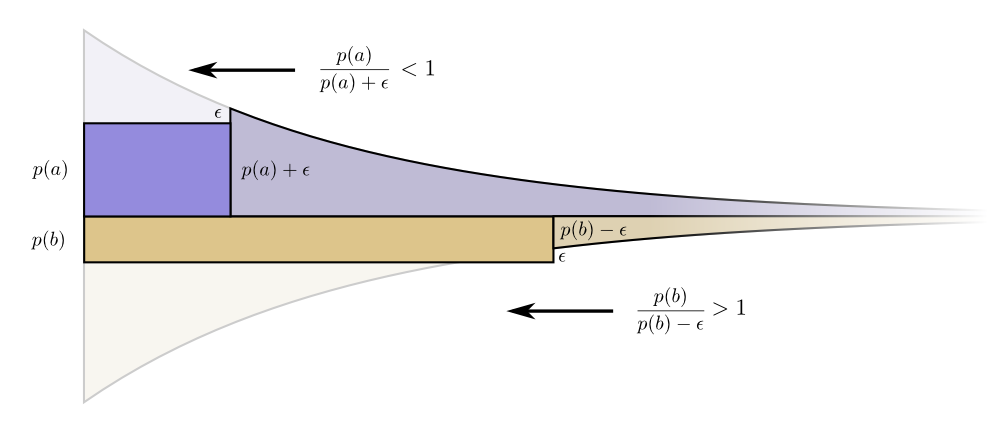
Les investisseurs crient: "Acheter !
Vendre (Un lecteur attentif peut avoir remarqué que dans le cas d'un budget optimal, des codes peuvent apparaître dans lesquels les mots de code sont fractionnaires. Qu'est-ce que cela signifie? En pratique, si vous souhaitez communiquer en envoyant un mot de code, vous devrez arrondir la valeur. Mais comment pouvons-nous voir plus tard, il y a un vrai sens à envoyer des mots de code fractionnaires lorsque nous en envoyons beaucoup en même temps!)PS La suite est consacrée à l'entropie, à l'entropie croisée, aux informations mutuelles, aux bits fractionnaires et à d'autres choses intéressantes.