SVM Explication à partir de zéro et implémentation en python. Analyse détaillée de la méthode des vecteurs supports

Bonjour à tous ceux qui ont choisi la voie du ML-Samurai!

Présentation:

Dans cet article, nous considérons la méthode de la machine à vecteurs de support ( Eng. SVM, Support Vector Machine ) pour le problème de classification. L'idée principale de l'algorithme sera présentée, le résultat de la définition de ses poids et une simple implémentation DIY seront analysés. Sur l'exemple d'un jeu de données $$$Iris$ le fonctionnement de l'algorithme écrit avec des données séparables / inséparables linéairement dans l'espace sera démontré $$$R ^ 2$ et visualisation de l'entraînement / pronostic. De plus, les avantages et les inconvénients de l'algorithme, ses modifications seront annoncées.

Figure 1. Photo open source d'une fleur d'iris

Le problème à résoudre:

Nous allons résoudre le problème de la classification binaire (quand il n'y a que deux classes). Premièrement, l'algorithme s'entraîne sur des objets de l'ensemble d'apprentissage, pour lesquels les étiquettes de classe sont connues à l'avance. En outre, l'algorithme déjà formé prédit l'étiquette de classe pour chaque objet à partir de l'échantillon différé / test. Les étiquettes de classe peuvent prendre des valeurs $$$Y = \ {- 1, +1 \}$ . Objet - vecteur avec N signes $$$x = (x_1, x_2, ..., x_n)$ dans l'espace $$$R ^ n$ . Lors de l'apprentissage, l'algorithme doit créer une fonction $$$F (x) = y$ qui prend un argument $$$x$ - un objet de l'espace $$$R ^ n$ et donne l'étiquette de classe $$$y$ .

Mots généraux sur l'algorithme:

La tâche de classification concerne l'enseignement avec un enseignant. SVM est un algorithme d'apprentissage avec un enseignant. Visuellement, de nombreux algorithmes d'apprentissage automatique peuvent être trouvés dans cet article de premier ordre (voir la section «Carte du monde de l'apprentissage automatique»). Il convient d'ajouter que SVM peut également être utilisé pour les problèmes de régression, mais le classificateur SVM sera analysé dans cet article.

L'objectif principal de SVM en tant que classificateur est de trouver l'équation d'un hyperplan de séparation
$$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 = 0$ dans l'espace $$$R ^ n$ , ce qui diviserait les deux classes de manière optimale. Vue générale de la transformation $$$F$ installation $$$x$ au libellé de classe $$$Y$ : $$$F (x) = signe (w ^ Tx-b)$ . Nous nous souviendrons que nous avons désigné $$$w = (w_1, w_2, ..., w_n), b = -w_0$ . Après avoir configuré les pondérations de l'algorithme $$$w$ et $$$b$ (formation), tous les objets tombant d'un côté de l'hyperplan construit seront prédits comme la première classe, et les objets tombant de l'autre côté - la deuxième classe.

Fonction intérieure $$$signe ()$ il y a une combinaison linéaire de caractéristiques de l'objet avec les poids d'algorithme, c'est pourquoi SVM fait référence à des algorithmes linéaires. Un hyperplan diviseur peut être construit de différentes manières, mais en poids SVM $$$w$ et $$$b$ sont configurés de telle sorte que les objets de classe se trouvent le plus loin possible de l'hyperplan de séparation. En d'autres termes, l'algorithme maximise l'écart ( marge anglaise ) entre l'hyperplan et les objets de classe qui en sont les plus proches. Ces objets sont appelés vecteurs de support (voir Fig. 2). D'où le nom de l'algorithme.

Figure 2. SVM (la base de la figure d'ici )

Une sortie détaillée des règles d'ajustement d'échelle SVM:

Afin de maintenir l'hyperplan de division aussi loin que possible des points d'échantillonnage, la largeur de bande doit être maximale. Vecteur $$$w$ Est le vecteur directeur de l'hyperplan diviseur. Ci-après, nous désignons le produit scalaire de deux vecteurs comme $$$\ langle a, b \ rangle$ ou $$$a ^ Tb$ .Trouvons la projection du vecteur dont les extrémités seront les vecteurs supports de différentes classes sur le vecteur direction de l'hyperplan. Cette projection montrera la largeur de la bande de séparation (voir Fig.3):

Figure 3. La sortie des règles de réglage des échelles (la base de la figure d'ici )

La marge de l' objet x à partir de la limite de classe est la valeur $$$M = y (w ^ Tx-b)$ . L'algorithme fait une erreur sur l'objet si et seulement si le retrait $$$M$ négatif (quand $$$y$ et $$$(w ^ Tx-b)$ différents caractères). Si $$$M ∈ (0, 1)$ , puis l'objet tombe à l'intérieur de la bande de séparation. Si $$$M> 1$ , alors l'objet x est correctement classé et est situé à une certaine distance de la bande de séparation. Nous écrivons cette connexion:

Le système résultant est le paramètre SVM par défaut avec un espace dur ( SVM à marge dure ), quand aucun objet n'est autorisé à entrer dans la bande de séparation. Il est résolu analytiquement par le théorème de Kuhn-Tucker. Le problème qui en résulte est équivalent au double problème de trouver le point de selle de la fonction Lagrange.

$$$$ afficher $$ \ left \ {\ begin {array} {ll} (w ^ Tw) / 2 \ rightarrow min & \ textrm {} \\ y (w ^ Tx-b) \ geqslant 1 & \ textrm {} \ end {array} \ right. $$ afficher $$

Tout cela est bon tant que nos classes sont linéairement séparables. Pour que l'algorithme puisse fonctionner avec des données linéairement inséparables, transformons un peu notre système. Laissez l'algorithme faire des erreurs sur les objets d'apprentissage, mais en même temps, essayez de conserver moins d'erreurs. Nous introduisons un ensemble de variables supplémentaires $$$\ xi _i> 0$ caractériser l'ampleur de l'erreur sur chaque objet $$$x_i$ . Nous introduisons une pénalité pour l'erreur totale dans la fonction minimisée:

$$$$ afficher $$ \ left \ {\ begin {array} {ll} (w ^ Tw) / 2 + \ alpha \ sum \ xi _i \ rightarrow min & \ textrm {} \\ y (w ^ Tx_i-b) \ geqslant 1 - \ xi _i & \ textrm {} \\ \ xi _i \ geqslant0 & \ textrm {} \ end {array} \ right. $$ afficher $$

Nous considérerons le nombre d'erreurs d'algorithme (lorsque M <0). Appelez ça une pénalité . Ensuite, la pénalité pour tous les objets sera égale au montant des amendes pour chaque objet $$$x_i$ où $$$[M_i <0]$ - fonction de seuil (voir Fig.4):

$$$$ afficher $$ [M_i <0] = \ left \ {\ begin {array} {ll} 1 & \ textrm {if} M_i <0 \\ 0 & \ textrm {if} M_i \ geqslant 0 \ end {tableau} \ droite. $$ afficher $$

Ensuite, nous rendons la pénalité sensible à l'ampleur de l'erreur et introduisons en même temps une pénalité pour l'approche de l'objet à la limite de classe:

Lors de l'ajout à l'expression de pénalité, le terme $$$\ alpha (w ^ Tw) / 2$ nous obtenons la fonction de perte SVM classique avec un espace doux ( SVM à marge douce ) pour un objet:

$$$Q$ - fonction de perte, c'est aussi une fonction de perte. C'est ce que nous allons minimiser à l'aide de la descente de gradient dans la mise en place des mains. Nous dérivons les règles de changement de poids, où $$$\ eta$ - étape de descente:

$$$$ afficher $$ \ bigtriangledown Q = \ left \ {\ begin {array} {ll} \ alpha w-yx & \ textrm {if} yw ^ Tx <1 \\ \ alpha w & \ textrm {if} yw ^ Tx \ geqslant 1 \ end {array} \ droite. $$ afficher $$

Questions possibles lors des entretiens (basées sur des événements réels):

Après des questions générales sur SVM: Pourquoi Hinge_loss maximise-t-il le jeu? - d'abord, rappelez-vous qu'un hyperplan change de position lorsque les poids changent $$$w$ et $$$b$ . Les poids de l'algorithme commencent à changer lorsque les gradients de la fonction de perte ne sont pas égaux à zéro (ils disent généralement: «les gradients s'écoulent»). Par conséquent, nous avons spécialement sélectionné une telle fonction de perte, dans laquelle les gradients commencent à couler au bon moment. $$$Perte de charnière$ ressemble à ceci: $$$H = max (0,1-y (w ^ Tx))$ . N'oubliez pas que le dégagement $$$m = y (w ^ Tx)$ . Quand l'écart $$$m$ assez grand ( $$$1$ ou plus) expression $$$(1 m)$ devient inférieur à zéro et $$$H = 0$ (par conséquent, les gradients ne coulent pas et le poids de l'algorithme ne change en aucune façon). Si l'écart m est suffisamment petit (par exemple, lorsqu'un objet tombe dans la bande de séparation et / ou est négatif (si la prévision de classification est incorrecte), alors Hinge_loss devient positif ( $$$H> 0$ ), les gradients commencent à couler et les poids des algorithmes changent. En résumé: les gradients s'écoulent dans deux cas: lorsque l'objet échantillon est tombé à l'intérieur de la bande de séparation et lorsque l'objet est mal classé.

Pour vérifier le niveau d'une langue étrangère, des questions similaires sont possibles: Quelles sont les similitudes et les différences entre LogisticRegression et SVM? - tout d'abord, nous parlerons de similitudes: les deux algorithmes sont des algorithmes de classification linéaire en apprentissage supervisé. Certaines similitudes se trouvent dans leurs arguments concernant les fonctions de perte: $$$log (1 + exp (-y (w ^ Tx)))$ pour logreg et $$$max (0,1-y (w ^ Tx))$ pour SVM (regardez l'image 4). Les deux algorithmes que nous pouvons configurer en utilisant la descente de gradient. Parlons maintenant des différences: SVM renvoie l'étiquette de classe de l'objet contrairement à LogReg, qui renvoie la probabilité d'appartenance à la classe. SVM ne peut pas fonctionner avec les étiquettes de classe $$$\ {0,1 \}$ (sans renommer les classes) contrairement à LogReg (fonction de perte LogReg pour $$$\ {0,1 \}$ : $$$-ylog (p) - (1-y) log (1-p)$ , où $$$y$ - véritable étiquette de classe, $$$p$ - retour de l'algorithme, probabilité d'appartenance à l'objet $$$x$ en classe $$$\ {1 \}$ ) Plus que cela, nous pouvons résoudre le problème SVM à marge dure sans descente de gradient. La tâche de recherche de vecteurs de support est réduite au point de selle de recherche dans la fonction Lagrange - cette tâche se réfère uniquement à la programmation quadratique.

import numpy as np import matplotlib.pyplot as plt %matplotlib inline xx = np.linspace(-4,3,100000) plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0') plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)') plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)') plt.title('Loss = F(Margin)') plt.grid() plt.legend(prop={'size': 14}); 

Figure 4. Fonctions de perte

Implémentation simple du SVM classique à marge souple:

Attention! Vous trouverez un lien vers le code complet à la fin de l'article. Vous trouverez ci-dessous des blocs de code sortis de leur contexte. Certains blocs ne peuvent être démarrés qu'après avoir travaillé sur les blocs précédents. Sous de nombreux blocs, des images seront montrées qui montrent comment le code placé au-dessus de cela a fonctionné.

 import numpy as np import warnings warnings.filterwarnings('ignore') import matplotlib.pyplot as plt import matplotlib.lines as mlines plt.rcParams['figure.figsize'] = (8,6) %matplotlib inline from sklearn.datasets import load_iris from sklearn.decomposition import PCA from sklearn.model_selection import train_test_split def newline(p1, p2, color=None): #    #function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib ax = plt.gca() xmin, xmax = ax.get_xbound() if(p2[0] == p1[0]): xmin = xmax = p1[0] ymin, ymax = ax.get_ybound() else: ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0]) ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0]) l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color) ax.add_line(l) return l 

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended class CustomSVM(object): __class__ = "CustomSVM" __doc__ = """ This is an implementation of the SVM classification algorithm Note that it works only for binary classification ############################################################# ###################### PARAMETERS ###################### ############################################################# etha: float(default - 0.01) Learning rate, gradient step alpha: float, (default - 0.1) Regularization parameter in 0.5*alpha*||w||^2 epochs: int, (default - 200) Number of epochs of training ############################################################# ############################################################# ############################################################# """ def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) def predict(self, X:np.array) -> np.array: y_pred = [] X_extended = add_bias_feature(X) for i in range(len(X_extended)): y_pred.append(np.sign(np.dot(self._w,X_extended[i]))) return np.array(y_pred) def hinge_loss(self, x, y): return max(0,1 - y*np.dot(x, self._w)) def soft_margin_loss(self, x, y): return self.hinge_loss(x,y)+self._alpha*np.dot(self._w, self._w) 

Nous considérons en détail le fonctionnement de chaque bloc de lignes:

1) créer une fonction add_bias_feature (a) , qui étend automatiquement le vecteur des objets, en ajoutant le nombre 1 à la fin de chaque vecteur, ce qui est nécessaire pour «oublier» le terme libre b. Expression $$$w ^ Tx-b$ équivalent à l'expression $$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 * 1$ . Nous supposons conditionnellement que l'unité est la dernière composante du vecteur pour tous les vecteurs x, et $$$w_0 = -b$ . Maintenant, régler les poids $$$w$ et $$$w_0$ Nous produirons en même temps.

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended 

2) nous décrirons ensuite le classificateur lui-même. Il a pour fonctions d'initialiser init () , d'apprendre fit () , de prédire predire () , de trouver la perte de la fonction hinge_loss () et de trouver la perte totale de la fonction de l'algorithme classique avec un soft gap soft_margin_loss () .

3) lors de l'initialisation, 3 hyperparamètres sont introduits: _etha - étape de descente de gradient ( $$$\ eta$ ), _alpha - coefficient de vitesse de réduction de poids proportionnelle (avant le terme quadratique dans la fonction de perte $$$\ alpha$ ), _epochs - le nombre d'époques d'entraînement.

  def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None 

4) pendant l'entraînement pour chaque époque de l'échantillon d'apprentissage (X_train, Y_train) nous prendrons un élément de l'échantillon, calculons l'écart entre cet élément et la position de l'hyperplan à un instant donné. De plus, en fonction de la taille de cet écart, nous changerons le poids de l'algorithme en utilisant le gradient de la fonction de perte $$$Q$ . Dans le même temps, nous calculerons la valeur de cette fonction pour chaque époque et combien de fois nous changerons de poids par époque. Avant de commencer la formation, nous nous assurerons que pas plus de deux étiquettes de classe différentes ne sont vraiment entrées dans la fonction d'apprentissage. Avant de configurer la balance, elle est initialisée en utilisant la distribution normale.

  def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) 

Vérification du fonctionnement de l'algorithme écrit:

Vérifiez que notre algorithme écrit fonctionne sur une sorte de jeu de données jouet. Prenez le jeu de données Iris. Nous préparerons les données. Désigner les classes 1 et 2 comme $$$+ 1$ et classe 0 as $$$-1$ . En utilisant l'algorithme PCA (explication et application ici ), nous réduisons de manière optimale l'espace de 4 attributs à 2 avec une perte de données minimale (il nous sera plus facile d'observer la formation et le résultat). Ensuite, nous nous diviserons en un échantillon de formation (train) et un échantillon retardé (validation). Nous allons nous entraîner sur l'échantillon d'entraînement, prévoir et vérifier les différés. Nous choisissons les facteurs d'apprentissage pour que la fonction de perte diminue. Au cours de la formation, nous examinerons la fonction de perte de la formation et l'échantillonnage retardé.

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y > 0).astype(int)*2-1 # [0,1,2] --> [False,True,True] --> [0,1,1] --> [0,2,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.005, alpha=0.006, epochs=150) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

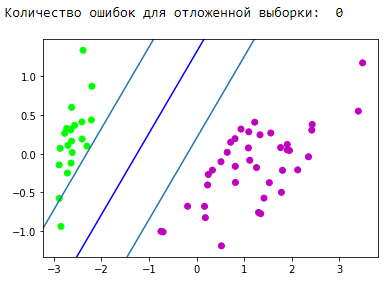
Super! Notre algorithme a traité des données linéairement séparables. Maintenant, séparez les classes 0 et 1 de la classe 2:

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y == 2).astype(int)*2-1 # [0,1,2] --> [False,False,True] --> [0,1,1] --> [0,0,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.03, alpha=0.0001, epochs=300) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors[:150]) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

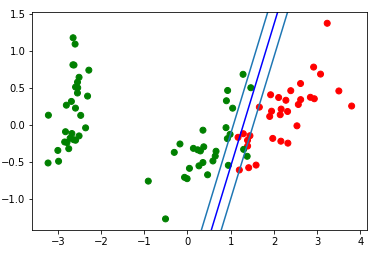
Regardons le gif, qui montrera comment la ligne de séparation a changé de position pendant l'entraînement (seulement 500 images pour changer de poids. Les 300 premières d'affilée. Les 200 pièces suivantes pour chaque 130ème image):

 import matplotlib.animation as animation from matplotlib.animation import PillowWriter def one_image(w, X, Y): axes = plt.gca() axes.set_xlim([-4,4]) axes.set_ylim([-1.5,1.5]) d1 = {-1:'green', 1:'red'} im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y]) im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue') # im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1 # im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 return im fig = plt.figure() ims = [] for i in range(500): if i<=300: k = i else: k = (i-298)*130 im = one_image(svm.history_w[k], X_train, Y_train) ims.append([im]) ani = animation.ArtistAnimation(fig, ims, interval=20, blit=True, repeat_delay=500) writer = PillowWriter(fps=20) ani.save("my_demo.gif", writer='imagemagick') 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

Redresser les espaces

Il est important de comprendre que dans les problèmes réels, il n'y aura pas de cas simple avec des données linéairement séparables. Pour travailler avec de telles données, l'idée de se déplacer vers un autre espace a été proposée, où les données seront linéairement séparables. Un tel espace est appelé rectification. La rectification des espaces et des noyaux ne sera pas affectée dans cet article. Vous pouvez trouver la théorie mathématique la plus complète dans 14,15,16 synopsis d'E. Sokolov et dans les conférences de K.V. Vorontsov .

Utilisation de SVM depuis sklearn:

En fait, presque tous les algorithmes classiques d'apprentissage automatique sont écrits pour vous. Donnons un exemple du code, nous prendrons l'algorithme de la bibliothèque sklearn .

 from sklearn import svm from sklearn.metrics import recall_score C = 1.0 # = self._alpha in our algorithm model1 = svm.SVC(kernel='linear', C=C) #model1 = svm.LinearSVC(C=C, max_iter=10000) #model1 = svm.SVC(kernel='rbf', gamma=0.7, C=C) #model1 = svm.SVC(kernel='poly', degree=3, gamma='auto', C=C) model1.fit(X_train, Y_train) y_predict = model1.predict(X_test) print(recall_score(Y_test, y_predict, average=None)) 

Avantages et inconvénients du SVM classique:

Avantages:

1. fonctionne bien avec un grand espace de fonctionnalités;
2. fonctionne bien avec de petites données;
3. Ainsi, l'algorithme trouve maximise la bande de division, ce qui, comme un airbag, peut réduire le nombre d'erreurs de classification;
4. puisque l'algorithme se réduit à résoudre le problème de programmation quadratique dans un domaine convexe, un tel problème a toujours une solution unique (l'hyperplan de séparation avec certains hyperparamètres de l'algorithme est toujours le même).

Inconvénients:

1. longue durée de formation (pour les grands ensembles de données);
2. instabilité du bruit: les valeurs aberrantes dans les données d'entraînement deviennent des objets intrus de référence et affectent directement la construction d'un hyperplan de séparation;
3. les méthodes générales de construction de noyaux et de rectification d'espaces les plus adaptées à un problème spécifique en cas d'inséparabilité linéaire des classes ne sont pas décrites. La sélection de transformations de données utiles est un art.

Application SVM:

Le choix de l'un ou l'autre algorithme d'apprentissage automatique dépend directement des informations obtenues lors de l'exploration de données. Mais en termes généraux, les tâches suivantes peuvent être distinguées:

• tâches avec un petit ensemble de données;
• tâches de classification de texte. SVM donne une bonne base de référence ([prétraitement] + [TF-iDF] + [SVM]), la précision des prévisions obtenue se révèle être au niveau de certains réseaux de neurones convolutionnels / récurrents (je recommande d'essayer cette méthode vous-même pour consolider le matériel). Un excellent exemple est donné ici, "Partie 3. Un exemple de l'une des astuces que nous enseignons" ;
• pour de nombreuses tâches avec des données structurées, le lien [ingénierie des fonctionnalités] + [SVM] + [noyau] "still cake";
• comme la perte de charnière est considérée comme assez rapide, elle peut être trouvée dans Vowpal Wabbit (par défaut).

Modifications de l'algorithme:

Il existe divers ajouts et modifications à la méthode du vecteur de support, visant à éliminer certains inconvénients:

• Machine à vecteur de pertinence (RVM)
• SVM 1 norme (LASSO SVM)
• SVM doublement régularisé (ElasticNet SVM)
• Fonctions de support Machine (SFM)
• Pertinence Caractéristiques Machine (RFM)

Sources supplémentaires sur SVM:

1. Conférences textuelles par K.V. Vorontsov
2. Résumés d'E. Sokolov - 14.15.16
3. Source cool par Alexandre Kowalczyk
4. Sur un habr il y a 2 articles consacrés à svm:
   
   • 2010 année
   • Année 2018
5. Sur le github, je peux mettre en évidence 2 implémentations SVM sympas aux liens suivants:
   
   • Algorithmes MLA d'un développeur national
   • ML-From-Scratch

Conclusion:

Merci beaucoup pour votre attention! Je serais reconnaissant pour tout commentaire, rétroaction et conseils.
Vous trouverez le code complet de cet article sur mon github .

ps Merci yorko pour des conseils sur le lissage des coins. Merci à Aleksey Sizykh - un département de physique et de technologie qui a partiellement investi dans le code.