Pendant des siècles, les chercheurs ont recherché des exemples de situations dans lesquelles les équations d'Euler pour l'hydrodynamique d'un fluide idéal s'avèrent incorrectes. Et enfin, les mathématiciens ont trouvé un tel exemple.
Depuis de nombreuses années, les mathématiciens soupçonnent que sous certaines conditions
les équations d'Euler refusent de fonctionner. Cependant, ils n'ont pas pu décrire le scénario spécifique dans lequel cela se produit. Jusqu'à aujourd'hui.
Ces équations sont une description mathématique idéalisée du mouvement des fluides. Dans certaines hypothèses, ils modélisent la propagation des vagues sur un étang ou l'infiltration de mélasse d'une canette. Ils devraient être capables de décrire le mouvement de n'importe quel liquide dans toutes les conditions - et pendant plus de deux siècles, ce fut le cas.
Cependant, de nouvelles preuves démontrent que sous certaines conditions, ces équations refusent toujours de fonctionner.
«Il y a un an et demi, je dirais que je ne m'attendais pas à voir un tel développement même de mon vivant», a déclaré
Tarek Elgindi , mathématicien de l'Université de Californie à San Diego, auteur d'un nouvel ouvrage.
Elgindi a prouvé l'existence de défauts dans les équations d'Euler dans deux ouvrages publiés en 2019 - il a écrit
avril lui-même et
octobre - en collaboration avec
Tejeddin Gole et
Nader Masmudi . Le travail a tourné sur un siècle d'hypothèses sur ces fameuses équations pour les liquides.
«Je pense que c'est une réalisation merveilleuse et merveilleuse», a déclaré
Peter Constantine , mathématicien à l'Université de Princeton.
Le travail d'Elgindi n'ouvre pas la fin des équations d'Euler. Cela prouve que dans certaines conditions, les équations semblent surchauffer et commencent à donner des bêtises. Mais dans des conditions plus réalistes, les équations restent jusqu'à présent invulnérables.
Cependant, l'exception trouvée par Elgindi a surpris les mathématiciens, car elle se produit dans des conditions dans lesquelles, comme on le pensait précédemment, l'équation devrait fonctionner de toute façon.
«En général, il me semble que les gens sont surpris par l'exemple donné par Tarek», a déclaré
Vlad Vikol , mathématicien à l'Université de New York.
Comment les équations d'Euler se sont précipitées
Leonhard Euler a dérivé les équations pour les liquides qui portent maintenant son nom en 1757. Ils décrivent l'évolution d'un fluide au fil du temps, tout comme les équations de Newton décrivent le mouvement d'une boule de billard sur une table.
Plus précisément, ces équations dénotent le mouvement instantané des particules infinitésimales d'un liquide. Leur description inclut la vitesse de la particule (à quelle vitesse et dans quelle direction elle se déplace) et une quantité qui y est liée comme le
tourbillon (la vitesse à laquelle la particule tourne à la manière d'un sommet et dans quelle direction).
Toutes ces informations forment entièrement un «champ de vitesse», un instantané du mouvement du fluide à un moment donné. Les équations d'Euler commencent par le champ de vitesse initial et prédisent comment il changera à tout moment dans le futur.
Tarek ElgindiLes équations d'Euler ne décrivent pas littéralement le fluide du monde réel. Il s'agit notamment de plusieurs hypothèses non physiques. Par exemple, ils ne fonctionnent que si les flux internes dans le fluide ne créent pas de friction, se déplaçant les uns par rapport aux autres. L'incompressibilité des liquides est également supposée, c'est-à-dire que, selon les règles des équations d'Euler, il est impossible de comprimer un liquide, après l'avoir placé dans un espace d'un volume plus petit que celui qu'il prend déjà.
"Ce modèle peut être imaginé comme un monde idéalisé, et les équations comme les règles pour le mouvement de ce monde", nous a écrit
Vladimir Sverak de l'Université du Minnesota par e-mail.
Ces conditions inhabituelles ont permis au mathématicien et physicien John von Neumann d'affirmer en plaisantant que ces équations simulent le comportement de «l'eau sèche». Pour simuler un fluide plus réaliste qui subit un frottement interne (la soi-disant viscosité), les chercheurs utilisent
les équations de Navier-Stokes .
«Les équations d'Euler sont très idéalisées. La friction est présente dans les vrais liquides », a expliqué Konstantin.
Mais en même temps, les équations d'Euler occupent toujours une place respectée dans la science. Les chercheurs aimeraient savoir si ces équations fonctionnent clairement dans le cadre de ce monde idéalisé sans frottement ni compression - c'est-à-dire, si elles peuvent décrire tous les états futurs de toutes les versions initiales possibles des champs de vitesse. Ou, en d'autres termes: existe-t-il un mouvement si fluide que ces équations ne peuvent pas être modélisées?
«À la base, la question est simple: ces équations font-elles toujours leur travail?», A déclaré Sverak.
En théorie, en remplaçant dans les équations les valeurs de l'état actuel du liquide, vous obtiendrez les valeurs exactes pour décrire son état futur. Ensuite, vous pouvez à nouveau remplacer ces nouvelles valeurs dans les équations et étendre votre prévision. Et généralement, un processus similaire peut être poursuivi pour n'importe quelle durée à l'avenir.
Cependant, il est également possible que, dans de très rares conditions, les équations se brisent. Ils peuvent grincer, souffler, produire des valeurs de sortie adaptées au rôle des futurs paramètres d'entrée, puis produire soudainement une valeur qui ne leur convient pas du tout. Dans de tels cas, les mathématiciens disent que les équations se sont "précipitées".
Si les équations d'Euler se précipitent, ce sera parce qu'elles commencent à augmenter la vitesse ou le tourbillon du point d'une manière peu naturelle. Ce gain sera si fort qu'en un temps fini la vitesse ou le vortex d'un point devient infini. Et dès que les équations donneront une valeur infinie, elles se décomposeront et cesseront de décrire les conditions environnementales à l'avenir. En effet, il est généralement impossible d'effectuer des calculs avec des valeurs infinies - cela revient à diviser par zéro (au fait, les valeurs de vitesse dans ce cas dépasseront la vitesse de la lumière - bien que dans le monde idéalisé du modèle, ce ne soit pas le pire).
Ces significations infinies fatidiques sont appelées «singularités». Lorsque les mathématiciens posent la question «Les équations d'Euler fonctionnent-elles toujours?», Ils demandent en fait «y a-t-il des scénarios dans lesquels les équations d'Euler donnent des singularités?»
De nombreux mathématiciens croient qu'il existe - cependant, à ce jour, ils n'ont pas pu trouver un scénario spécifique dans lequel les équations explosent vraiment.
"Il y avait un sentiment qu'Euler essayait d'éviter la singularité, et jusqu'à récemment, il a réussi", a déclaré Konstantin.
Le nouveau travail ne montre pas comment les équations donnent des singularités dans les conditions qui intéressent le plus les mathématiciens. Cependant, jusqu'à présent, ce résultat est plus proche de l'objectif que les autres. Et pour cela, Elgindi a considéré un modèle simplifié de mouvement fluide.
Réduire la complexité
Les mathématiciens ont différentes manières de réduire la complexité du mouvement des fluides, pour la simulation desquels ils utilisent les équations d'Euler. Bon nombre des résultats les plus intéressants, similaires à ceux obtenus par Elgindi, incluent une démonstration de la façon dont vous pouvez simplifier le comportement du fluide - c'est-à-dire, combien vous pouvez simplifier les données substituées dans les équations - tout en étant en mesure de dire quelque chose de significatif sur les équations elles-mêmes.
Dans un véritable fluide tridimensionnel, comme l'eau dans un étang, toute particule a trois axes de mouvement possibles: l'axe x (gauche-droite), l'axe y (haut-bas) et l'axe z (avant-arrière). Beaucoup de liberté de mouvement. De plus, le mouvement des particules dans une partie du liquide ne sera pas nécessairement fortement associé au mouvement des particules dans une autre partie.
"Vous devez garder une trace de trop", a déclaré Elgindi.
Dans le nouvel article, Elgindi simplifie le travail pour les équations d'Euler. Cela nécessite que le liquide soit symétrique le long de l'axe z, ce qui n'est généralement pas présent dans les vrais liquides. En raison de la symétrie, il devient plus facile de calculer le champ de vitesse, car il est connu que les points des deux côtés de l'axe z sont symétriques miroir. Par conséquent, si vous connaissez la vitesse ou le tourbillon d'un point, il vous suffit de modifier le signe de ces valeurs et d'obtenir ces valeurs pour un autre point.
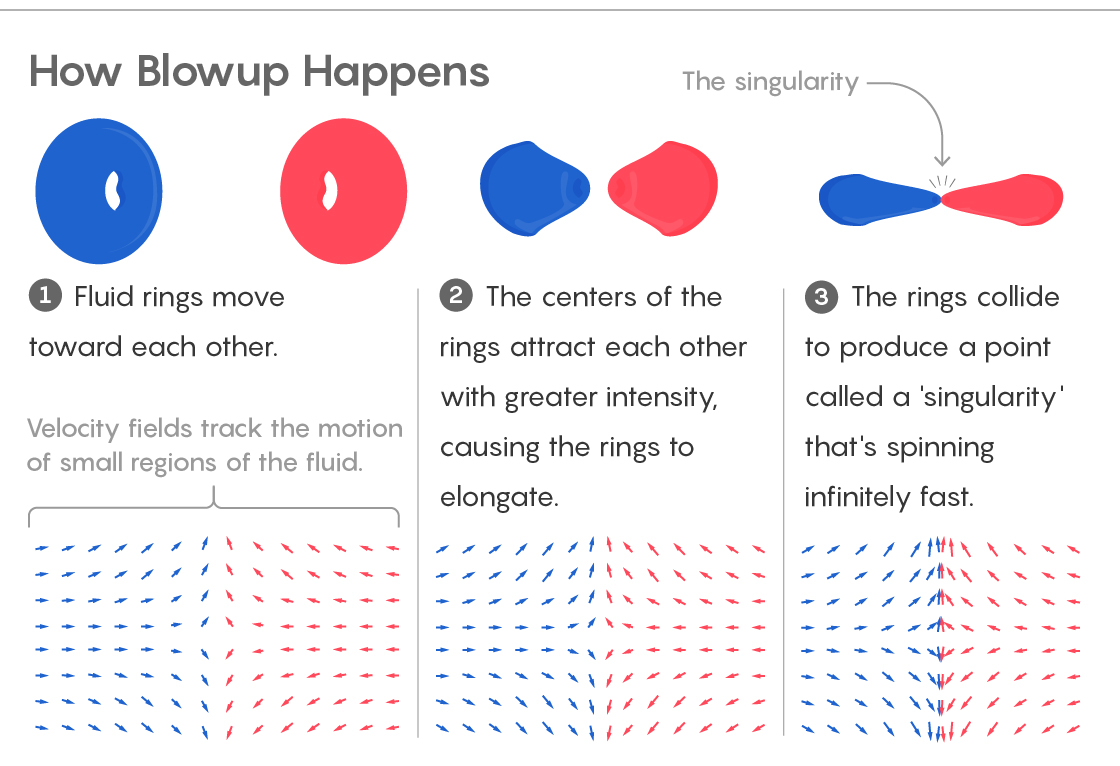1) Les fluides se déplacent vers. Les champs de vitesse suivent le mouvement de petites sections de fluide.
2) Les centres des anneaux sont attirés, ce qui provoque l'étirement des anneaux.
3) Les anneaux entrent en collision, créant un point de "singularité", tournant à une vitesse infinie.Elle limite également le mouvement éventuel de points dans le fluide. Les particules peuvent être déplacées le long de l'axe z, ou en être éloignées, ou vers lui. Ils ne peuvent pas tourner autour de l'axe z. Les mathématiciens disent qu'il n'y a pas de tourbillons dans de tels liquides.
"Cela réduit la tâche à deux dimensions", a déclaré Elgindi.
Enfin, Elgindi impose quelques conditions supplémentaires aux données initiales introduites dans les équations d'Euler. Dans un sens, ces données sont plus grossières que celles qui décrivent des fluides réels et augmentent la probabilité de formation de singularités.
Dans la vraie vie, si vous vous déplacez d'un point à un autre, situé très près de lui, les vitesses de ces deux points seront presque égales. Les tourbillons de ces deux points devraient également être très similaires. Les mathématiciens disent que les champs de vitesse avec cette propriété sont «lisses», c'est-à-dire que les valeurs sur eux changent progressivement - ou en douceur - lorsqu'ils se déplacent d'un point à un autre. Pas de changements rapides.
Mais dans le cas de la description du liquide d'Elgindi, tout est différent.
"La torsion dans les données de Tarek peut changer beaucoup", a déclaré Vikol. «Les points proches peuvent avoir des tourbillons très différents.»
Il peut sembler que les simplifications d'Elgindi s'écartent beaucoup du comportement des vrais liquides pour être utiles. Cependant, ils sont encore beaucoup moins rigides que la plupart des scénarios simplifiés dans lesquels les scientifiques considéraient auparavant les équations d'Euler. En fait, Elgindi a même montré que dans ces conditions simplifiées, mais pas trop, les équations d'Euler commencent à produire des résultats très inattendus.
Game over
Pour comprendre la découverte d'Elgindi, imaginez un récipient d'eau. Ce n'est pas un exemple exact, car le travail d'Elgindi considère les liquides sans limites, c'est-à-dire volant comme une bulle en apesanteur. Mais afin de visualiser le scénario, qui est au centre de son travail, il sera utile de disposer l'eau dans le réservoir. Bien que les hypothèses mathématiques les plus importantes - et celles qui sont les plus difficiles à prouver - concernent les liquides sans frontières.
Imaginez ensuite deux épais anneaux d'eau situés à différentes extrémités du réservoir. Ils forment de petits entonnoirs, tels que des tourbillons - des perturbations organisées à l'intérieur du fluide. Des phénomènes similaires se retrouvent dans la nature et sont similaires aux anneaux de fumée que les fumeurs expérimentés peuvent donner.
Imaginez maintenant comment deux anneaux opposés se rejoignent.
Pendant l'approche, les équations d'Euler fonctionnent normalement, en comptant les champs de vitesse qui décrivent le fluide à chaque instant. Mais quand ils se rapprochent suffisamment, les équations commencent à produire des résultats très étranges.
Ils montrent comment les anneaux commencent à être attirés de plus en plus - et les points centraux des anneaux sont attirés les uns aux autres encore plus que les parties extérieures. En conséquence, les anneaux sont étendus et commencent à ressembler à un entonnoir. Et plus les centres des anneaux se rapprochent, plus leur vitesse augmente. Et puis ils entrent en collision.
Et si en ce moment vous regardez le champ de vitesse qui décrit la collision, vous pouvez voir qu'avec cet ensemble d'hypothèses dans toute l'histoire des équations d'Euler, personne n'a vu: la singularité. Elgindi a prouvé que les équations d'Euler donnent une vitesse infinie au point de collision. Le jeu est terminé.
"La forme classique de l'équation se brise", a déclaré Elgindi. "Après cela, ce n'est pas clair ce qui se passe."
Le résultat a ses limites. À savoir, il est impossible d'extrapoler le comportement des équations d'Euler dans des conditions complètement «lisses» sur la base de ce résultat. Il y a quelques décennies, les mathématiciens ont prouvé que dans des conditions "douces", le scénario envisagé par Elgindi ne produirait pas de singularité.
Cependant, le reste de son résultat change complètement la vision des mathématiciens sur ces anciennes équations.
Avant les travaux d'Elgindi, les mathématiciens ne pouvaient prouver l'existence d'aucune situation dans un fluide sans frontières, dans lequel les équations d'Euler fonctionnent pendant un certain temps (pendant que les anneaux se rejoignent), mais pas à l'infini. Dans tous les travaux précédents, les mathématiciens se sont avérés que si les équations fonctionnent fondamentalement, alors elles fonctionnent toujours.
«C'est un résultat très remarquable, car il prouve la présence de singularités dans le scénario, que nous appelons« correctement défini ».» Cela a du sens, mais en même temps, nous arrivons à une singularité dans un temps fini », a déclaré Konstantin.
De nombreuses générations de scientifiques ont cherché un point faible dans les équations d'Euler. Et enfin - avec quelques réserves - le mathématicien l'a trouvé.