À propos de la signification géométrique des codes Gray

Les codes gris sont étroitement liés à la courbe de Hilbert .

Cependant, lors de la communication avec des collègues, il s'est avéré que cette simple dépendance semble à leurs yeux quelque chose de non trivial. Une recherche sur Internet au hasard n'a rien donné d'autre qu'une phrase boueuse sur le wiki: «Les courbes de Hilbert dans des espaces de plus grande dimension sont représentatives de généralisations de codes Gray». Par conséquent, il y avait un désir d'ouvrir le sujet - brièvement, dans un langage simple.

En conséquence, sous la coupe - "scandales, intrigues, enquêtes".

La principale caractéristique du code Gray est que deux valeurs lexicographiquement adjacentes ne diffèrent que dans une seule catégorie. En revanche, la courbe de Hilbert est continue - la distance entre deux points adjacents est toujours égale à un. Cela seul fait allusion à leur connexion intérieure.

Le code Gray décrit les occurrences d'une courbe de Hilbert dans un seul hypercube. En fait, si nous prenons un code à 3 bits et le dessinons dans un espace à 3 dimensions (en prenant chaque bit pour la coordonnée correspondante), nous obtenons


Figure 1 Code Gray à 3 bits sous forme de cube en 3 dimensions

L'image familière est le simplexe tridimensionnel de la courbe de Hilbert! Remplaçant successivement chaque noeud du simplex par le même simplex (en tenant compte des rotations et réflexions pour maintenir la continuité), on obtient une courbe de Hilbert 4x4x4.

En poursuivant ces itérations, nous pouvons remplir en continu un réseau cubique de n'importe quelle taille.


Figure 2 plusieurs itérations du simplexe de la courbe de Hilbert.

Mais comment est-ce arrivé?

On sait que le code Gray est auto-similaire. Il est parfois appelé miroir «du fait que la première moitié des valeurs lors du changement de l'ordre est équivalente à la seconde moitié, à l'exception du bit haut. Le bit le plus significatif est simplement inversé. » Pour plus de clarté, le code 3 bits est le bit le plus significatif - le plus à gauche:



Puisque nous parlons d'auto-similitude, commençons par le début - avec un code à un bit. À strictement parler, il serait possible de commencer avec une dimension zéro - des points, cela ne change fondamentalement rien, seuls les mots devraient être écrits davantage.

Le code à un chiffre de Gray est encore plus simple qu'un fusil à trois lignes, c'est 0 ou 1.

Géométriquement, cela correspond à un cube unitaire unidimensionnel - un segment. Vous pouvez vous déplacer le long d'un segment soit du début à la fin, soit de la fin au début - jusqu'à la symétrie, c'est la même chose. Mais néanmoins, nous appellerons le début l'endroit où la valeur est moindre (rappelez-vous que les côtés du cube sont des chiffres du nombre), et la fin - où elle est plus.

Nous passons au cas bidimensionnel. Un cube à deux dimensions est un carré. En tenant compte de l'auto-similitude, nous clonons le cube unidimensionnel (0,1) et obtenons deux segments - (0,0 -> 1,0) et (0,1 -> 1,1). Vous devez maintenant connecter ces segments pour contourner le carré. Et ici, deux options se présentent:

• nous connectons le début de l'itération précédente - le cube unidimensionnel avec le début de son clone. Jusqu'à la symétrie, cela revient à connecter l'extrémité à l'extrémité. Le type de symétrie est le miroir. Cette option est appelée conditionnellement «missionnaire».
  
• nous connectons la fin de l'itération précédente au début de son clone. Jusqu'à la symétrie, cela revient à joindre le début d'une ligne à la fin d'un clone. Le type de symétrie est central. Nous appelons cette option un «train».

Nous agissons de manière similaire en passant à des cas tridimensionnels ou plus.


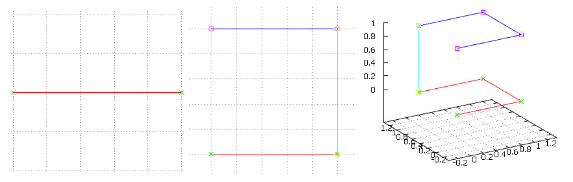Figure 3 Les deux premières itérations de la version «missionnaire»

Ici, l'itération précédente est surlignée en rouge, son clone est en bleu et leur connexion est en turquoise.

Notez que la connexion passe toujours par une seule dimension - la nouvelle ajoutée, d'où la principale caractéristique du code Gray apparaît en raison de l'auto-similitude. Et puisque la fin de l'itération précédente est liée à la fin de son clone, la «mise en miroir» se produit - lorsque nous nous déplaçons, nous sommes obligés de parcourir le clone dans l'ordre inverse. Quelle que soit la dimension. Ici, vous pouvez voir l'origine et les caractéristiques de la courbe de Hilbert - quelle que soit la taille du réseau (quelle que soit sa dimension), au niveau local, il s'agit toujours du même cube unitaire avec des transitions de longueur un.


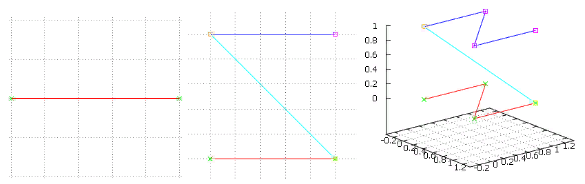Figure 4 Les deux premières itérations de l'option «train», les mêmes couleurs

Mais cette musique nous est également familière - nous avons obtenu une courbe en Z simplex. Le mot simplex ici signifie également que si nous prenons chacun de ses points et le remplaçons par un simplex, nous obtenons un cube 4x4x4, en continuant les itérations - nous pouvons remplir un réseau cubique arbitrairement grand.

Il est amusant que dans ce cas, la conversion du chemin passé de l'origine au code, qui peut être analysé en bits, soit triviale.
Alors que le cas du code Gray est G = W ^ (W >> 1), où W est la longueur passée, G est le code Gray.


Figure 5 deux premières itérations de la courbe en Z (wiki)


6 à titre de comparaison, les deux premières itérations de la courbe de Hilbert (wiki)

Mais il n'y a pas d'autres options (naturelles) pour contourner un seul hypercube.
Il s'avère donc que partout où vous jetez, autour de Hilbert, Lebesgue ... et du vide .

PS : dans l'image du titre, un encodeur circulaire avec un code Gray à huit chiffres.
PPS : ici, ils me corrigent que le simplexe est un terme bien établi, ce n'est pas bon avec lui. Eh bien, cet article n'est pas seulement un simplexe, mais un simplexe d'une courbe de Hilbert ou un simplexe d'une courbe en Z. Que les mathématiciens fidèles me pardonnent.