Théorie de l'information visuelle (partie 2)

La deuxième partie de la traduction du Longrid consacrée à la visualisation des concepts de la théorie de l'information. La deuxième partie traite de l'entropie, de l'entropie croisée, de la divergence de Kullback-Leibler, des informations mutuelles et des bits fractionnaires. Tous les concepts sont fournis avec d'excellentes explications visuelles.

Pour l'exhaustivité de la perception, avant de lire la deuxième partie, je vous recommande de vous familiariser avec la première .

Calcul d'entropie

Rappelons que le coût d'un message est long $$$L$ est égal à $$$\ frac {1} {2 ^ L}$ . nous pouvons inverser cette valeur pour obtenir la longueur du message qui vaut le montant donné: $$$\ log_2 (\ frac {1} {cost})$ . Puisque nous dépensons $$$p (x)$ par mot de code pour $$$x$ , la longueur sera égale $$$\ log_2 (\ frac {1} {p (x)})$ . Dans la figure, le choix des meilleures longueurs de mots de code.



Nous avons discuté précédemment qu'il existe une limite fondamentale à la longueur d'un message moyen pour transmettre des événements à partir d'une distribution de probabilité donnée $$$p$ . cette limite, la longueur moyenne des messages lors de l'utilisation du meilleur système de codage, est appelée entropie $$$p, H (p)$ . Maintenant que nous connaissons la longueur optimale du mot de code, nous pouvons la calculer!

$$

$$H (p) = \ sum_xp (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

(Souvent, l'entropie s'écrit $$$H (p) = - \ sum p (x) \ log_2 (p (x))$ en utilisant l'égalité $$$\ log (1 / a) = - \ log (a)$ . Il me semble que la première version est plus intuitive, nous allons donc continuer à l'utiliser.)

Si je veux signaler l'événement qui s'est produit, quoi que je fasse, j'ai en moyenne besoin d'envoyer autant de bits.

La quantité moyenne d'informations nécessaires pour transmettre quelque chose a des conséquences directes sur la compression. Mais y a-t-il d'autres raisons pour lesquelles nous devrions nous en occuper? Oui! Il décrit mon incertitude et permet de quantifier l'information.

Si je savais avec certitude ce qui se passerait, je n'aurais pas à envoyer de message du tout! S'il y a deux choses qui peuvent arriver avec une probabilité de 50%, je n'ai besoin d'envoyer qu'un bit. Mais s'il y a 64 événements différents qui peuvent se produire avec la même probabilité, je devrai envoyer 6 bits. Plus la probabilité est concentrée, plus j'ai de possibilités de créer du code intelligent avec des messages courts et moyens. Plus la probabilité est vague, plus mes messages devraient être longs.

Plus le résultat est incertain, plus j'apprends en moyenne quand ils me disent ce qui s'est passé.

Entropie croisée

Peu avant de déménager en Australie, Bob a épousé Alice, également imaginaire. À ma grande surprise, ainsi qu'à la surprise d'autres personnages dans ma tête, Alice n'était pas un amoureux des chiens. Elle adorait les chats. Malgré cela, ils ont pu trouver un langage commun dans leur obsession générale pour les animaux et leur vocabulaire très limité.



Ces deux-là utilisent les mêmes mots, mais avec des fréquences différentes. Bob parle tout le temps de chiens, Alice parle tout le temps de chats.

Alice m'a d'abord envoyé des messages en utilisant le code de Bob. Malheureusement, ses postes étaient plus longs que nécessaire. Le code de Bob a été optimisé pour sa distribution de probabilité. Alice a une distribution de probabilité différente et le code n'est pas optimal pour elle. La longueur moyenne des mots de code lorsque Bob utilise son code est de 1,75 bits; quand Alice l'utilise, puis 2,25. Ce serait encore pire si les deux n'étaient pas si similaires!

La longueur moyenne des messages d'une distribution avec le code optimal pour une autre distribution est appelée entropie croisée. Formellement, nous pouvons définir l'entropie croisée comme suit:

$$

$$H_p (q) = \ sum_xq (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

Dans ce cas, nous parlons de l'entropie croisée de la fréquence des mots du catworm d'Alice par rapport à la fréquence des mots de l'amant de chien de Bob.



Pour réduire le coût de notre connexion, j'ai demandé à Alice d'utiliser son propre code. À mon grand soulagement, cela a réduit la longueur moyenne des messages. Mais cela a créé un nouveau problème: parfois, Bob a utilisé accidentellement le code d'Alice. Étonnamment, c'est pire quand Bob utilise le code d'Alice que quand Alice utilise le code de Bob!

Nous avons donc maintenant quatre possibilités:

• Bob utilise du code natif ( $$$H (p) = 1,75$ peu)
• Alice utilise le code de Bob ( $$$H_p (q) = 2,25$ peu)
• Alice utilise son propre code ( $$$H (q) = 1,75$ peu)
• Bob utilise le code d'Alice ( $$$H_q (p) = 2,375$ peu)

Ce n'est pas aussi intuitif qu'on pourrait le penser. Par exemple, nous pouvons voir que $$$H_p (q) ≠ H_q (p)$ . Pouvons-nous en quelque sorte voir comment ces quatre significations sont liées les unes aux autres?

Dans le diagramme suivant, chaque sous-graphique représente l'une de ces 4 possibilités. Les illustrations visualisent la longueur moyenne d'un message. Ils sont organisés dans un carré, de sorte que si les messages proviennent de la même distribution, les graphiques sont à proximité et s'ils utilisent les mêmes codes, ils sont superposés. Cela vous permet de combiner visuellement les distributions et les codes.



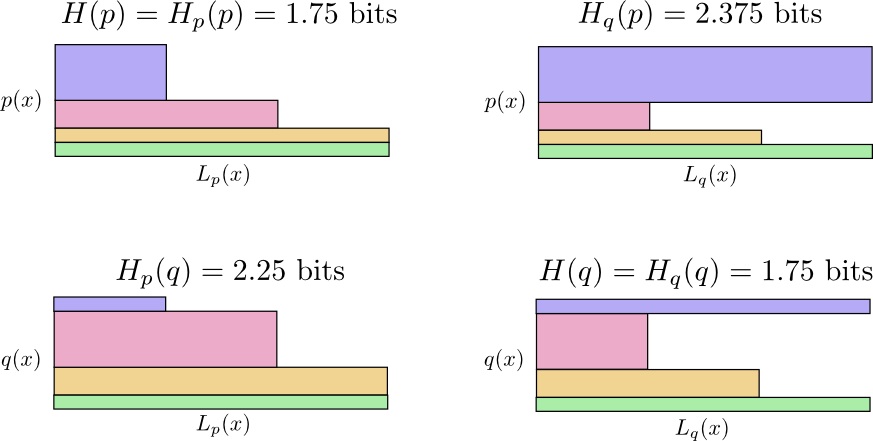
Voyez pourquoi $$$H_p (q) ≠ H_q (p)$ ? $$$H_q (p)$ si grand, parce que l'événement marqué en bleu se produit souvent lorsque $$$p$ mais obtient un long mot de code car il est très rare pour $$$q$ . D'autre part, des événements fréquents avec $$$q$ moins fréquent avec $$$p$ mais la différence est moins dramatique, donc $$$H_p (q) Hp (q)$ un peu moins.

L'entropie croisée n'est pas symétrique.

Alors, pourquoi devriez-vous vous soucier de l'entropie croisée? L'entropie croisée nous permet d'exprimer la différence entre les deux distributions de probabilité. Plus les distributions sont différentes $$$p$ et $$$q$ l'entropie croisée supérieure $$$p$ concernant $$$q$ il y aura plus d'entropie $$$p$ .



De même, plus $$$q$ différent de $$$p$ l'entropie croisée supérieure $$$q$ concernant $$$p$ il y aura plus d'entropie $$$q$ .

La chose vraiment intéressante est la différence entre l'entropie et l'entropie croisée. Cette différence est égale à la durée de nos publications, car nous avons utilisé du code optimisé pour une autre distribution. Si les distributions sont les mêmes, cette différence sera nulle. Au fur et à mesure que les différences augmentent, elles deviendront plus importantes.

Nous appelons cette différence divergence Kullback-Leibler, ou simplement divergence KL. Divergence KL $$$p$ concernant $$$q$ , $$$D_q (p)$ défini comme suit:

$$

$$D_q (p) = H_q (p) - H (p)$$

La grande chose au sujet de la divergence KL est qu'elle ressemble à la distance entre deux distributions. Il mesure à quel point ils sont différents! (Si vous prenez cette idée au sérieux, vous arriverez à la géométrie de l'information.)

L'entropie croisée et la divergence KL sont incroyablement utiles dans l'apprentissage automatique. Nous voulons souvent qu'une distribution soit proche d'une autre. Par exemple, nous pouvons vouloir que la distribution prédite soit proche de la vérité sous-jacente. La divergence KL nous donne un moyen naturel de le faire, et donc elle se manifeste partout.

Entropie et plusieurs variables

Revenons à notre exemple météo et vêtements donné plus haut:




Ma mère, comme beaucoup de parents, s'inquiète parfois de ne pas m'habiller correctement pour la météo. (Elle a de bonnes raisons d'être soupçonnée - je ne porte parfois pas d'imperméable en hiver.) Par conséquent, elle veut souvent connaître la météo et ce que je porte. Combien de bits dois-je lui envoyer pour signaler cela?

La façon la plus simple d'y penser est d'équilibrer la distribution de probabilité:



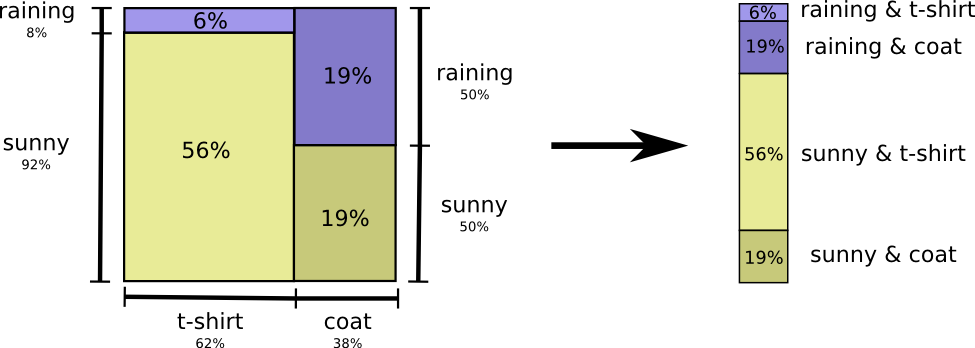
Maintenant, nous pouvons calculer les mots de code optimaux pour les événements avec de telles probabilités et calculer la longueur moyenne des messages:



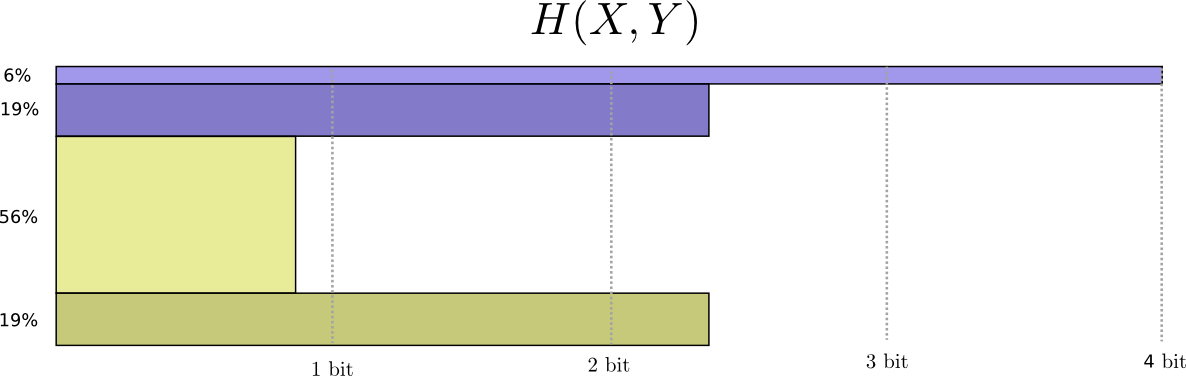
Nous l'appelons l'entropie conjointe $$$X$ et $$$Y$ défini comme suit:

$$

$$H (X, Y) = \ sum_ {x, y} p (x, y) \ log_2 \ bigg (\ frac {1} {p (x, y)} \ bigg)$$

Elle coïncide avec notre définition habituelle, à l'exception de deux variables au lieu d'une.

Une image légèrement meilleure de ceci, sans égaliser la distribution, est obtenue en représentant la longueur du mot de code dans la troisième dimension. L'entropie, c'est du volume!



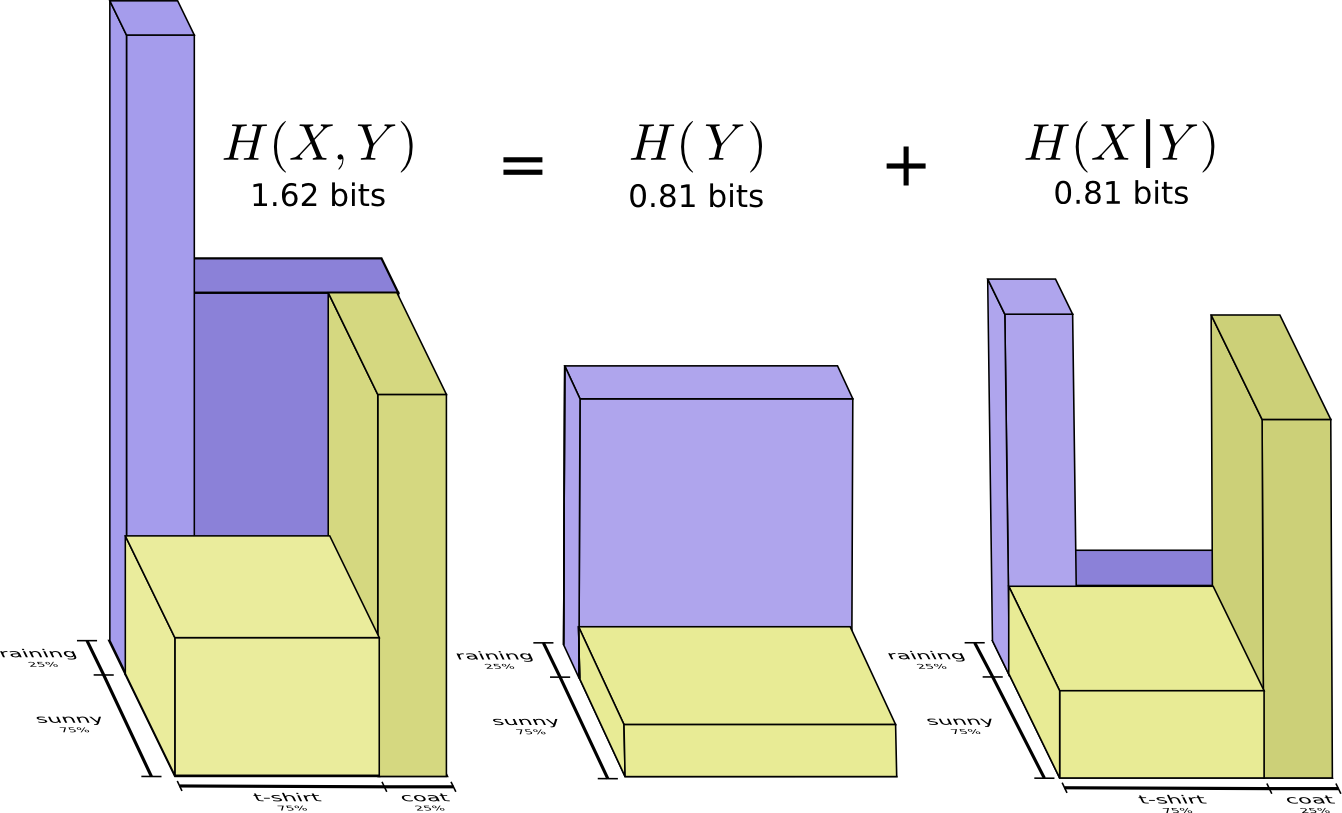
Mais supposons que ma mère connaisse déjà le temps. Elle peut la regarder dans les actualités. Combien d'informations dois-je fournir?

On dirait que je dois envoyer suffisamment d'informations pour me dire quels vêtements je porte. Mais en fait, je dois envoyer moins d'informations, car la météo que je porterai dépend beaucoup de la météo! Regardons le cas de la pluie et du soleil séparément.



Dans les deux cas, je n'ai pas besoin d'envoyer trop d'informations en moyenne, car la météo me donne une bonne idée de la bonne réponse. Quand le soleil, je peux utiliser un code spécial optimisé pour le soleil, et quand il pleut, je peux utiliser le code optimisé pour la pluie. Dans les deux cas, j'envoie moins d'informations que si j'utilisais un code commun pour les deux. Pour obtenir la quantité moyenne d'informations que je dois envoyer à ma mère, je viens de rassembler ces deux cas ...



Nous appelons cette entropie conditionnelle. Si vous le formalisez en une équation, vous obtenez:

$$

$$H (X | Y) = \ sum_yp (y) \ sum_xp (x | y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

$$

$$= \ sum_ {x, y} p (x, y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

Information mutuelle

Dans la section précédente, nous avons découvert que la connaissance d'une variable peut signifier que moins d'informations sont nécessaires pour communiquer la valeur d'une autre variable.

Une bonne façon d'y penser est d'imaginer la quantité d'informations sous forme de rayures. Ces bandes se chevauchent s'il existe des informations communes entre elles. Par exemple, certaines des informations $$$X$ et $$$Y$ commun donc $$$H (X)$ et $$$H (Y)$ sont des rayures qui se chevauchent. Et depuis $$$H (X, Y)$ Est l'information des deux variables, alors c'est l'union des bandes $$$H (X)$ et $$$H (Y)$ .



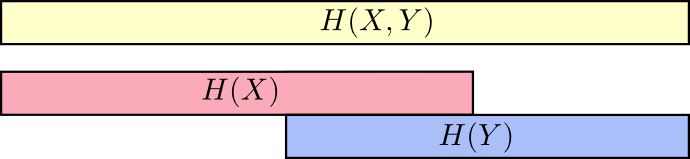
Quand nous pensons aux choses de cette façon, beaucoup devient plus facile à voir.

Par exemple, nous avons déjà noté que pour transmettre des informations $$$X$ donc et $$$Y$ («Entropie conjointe», $$$H (X, Y)$ ) plus d'informations sont nécessaires que pour la transmission uniquement $$$X$ («Entropie ultime», $$$H (X)$ ) Mais si vous savez déjà $$$Y$ puis pour la transmission $$$X$ («Entropie conditionnelle», $$$H (X | Y)$ ) moins d'informations sont nécessaires que si vous ne le saviez pas!



Cela semble compliqué, mais si vous traduisez en groupes, tout se révèle très simple. $$$H (X | Y)$ Les informations que nous devons envoyer pour informer $$$X$ celui qui sait déjà $$$Y$ informations dans $$$X$ qui n'est pas non plus $$$Y$ . Visuellement, cela signifie que $$$H (X | Y)$ - cela fait partie de la bande $$$H (X)$ qui ne chevauche pas $$$H (Y)$ .

Vous pouvez maintenant lire l'inégalité $$$H (X, Y) ≥H (X) ≥H (X | Y)$ à droite sur le graphique suivant.



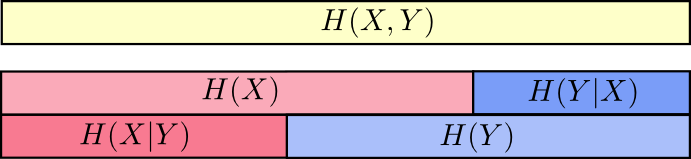
Une autre égalité est la suivante - $$$H (X, Y) = H (Y) + H (X | Y)$ . C'est-à-dire informations dans $$$X$ et $$$Y$ ce sont des informations dans $$$Y$ plus d'informations dans $$$X$ qui n'est pas en $$$Y$ .



Encore une fois, cela est difficile à voir dans les équations, mais facile à voir si vous pensez en termes de bandes d'informations qui se chevauchent.

À ce stade, nous avons divisé les informations en $$$X$ et $$$Y$ de plusieurs façons. Nous connaissons les informations de chaque variable, $$$H (X)$ et $$$H (Y)$ . Nous connaissons la combinaison d'informations dans les deux $$$H (X, Y)$ . Nous avons des informations qui sont dans une variable mais pas dans une autre, $$$H (X | Y)$ et $$$H (Y | X)$ . Une grande partie de cela tourne autour des informations communes aux variables - l'intersection de leurs informations. Nous l'appelons «information mutuelle» $$$I (x, y)$ défini comme:

$$

$$I (X, Y) = H (X) + H (Y) −H (X, Y)$$

Cette définition est vraie car $$$H (X) + H (Y)$ contient deux copies d'informations mutuelles, car il est également situé dans $$$X$ et dans $$$Y$ tout $$$H (X, Y)$ contient une seule copie. (voir schéma précédent)

La variation de l'information est étroitement liée à l'information mutuelle. La variation de l'information est une information qui n'est pas commune aux variables. Nous pouvons le définir comme ceci:

$$

$$V (X, Y) = H (X, Y) −I (X, Y)$$

La variation de l'information est intéressante en ce qu'elle nous donne une métrique, le concept de la distance entre différentes variables. La variation de l'information entre deux variables est nulle si la connaissance de la valeur d'une variable vous indique la signification de l'autre et devient plus grande à mesure qu'elles deviennent plus indépendantes.

Comment est-ce lié à la divergence KL, qui nous donne également le concept de distance? La divergence KL est la distance entre deux distributions sur la même variable ou le même ensemble de variables. Au contraire, la variation de l'information nous donne la distance entre deux variables co-distribuées. La divergence KL est un écart entre les distributions, une variation des informations au sein d'une distribution.

Nous pouvons tout rassembler dans un seul diagramme reliant tous ces différents types d'informations:

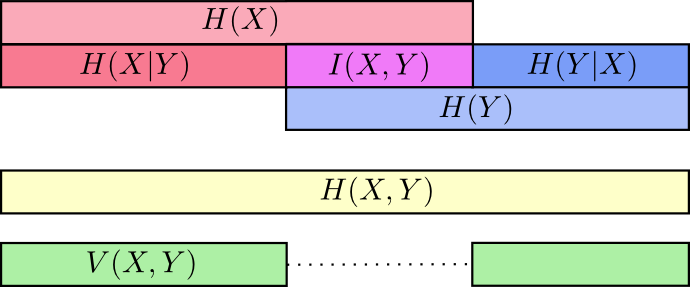
Bits de fraction

Une chose très peu intuitive dans la théorie de l'information est que nous pouvons avoir des nombres fractionnaires de bits. C'est assez bizarre. Que veut dire un peu?

Voici une réponse simple: souvent, nous nous intéressons à la longueur moyenne d'un message, plutôt qu'à la longueur d'un message particulier. Si dans la moitié des cas, un bit est envoyé et dans la moitié des cas deux, alors en moyenne, un bit et demi est envoyé. Il n'y a rien d'étrange dans le fait que les moyennes peuvent être fractionnaires.

Mais avec cette réponse, nous évitons la question. Souvent, les longueurs de mot de code optimales sont également fractionnaires. Qu'est-ce que cela signifie?

Pour être précis, regardons la distribution de probabilité, où un événement, $$$a$ arrive 71% du temps, et un autre événement, $$$b$ survient 29% du temps.



Le code optimal utilisera 0,5 bit pour représenter $$$a$ et 1,7 bits pour représenter $$$b$ . Eh bien, si nous voulons envoyer un seul de ces mots de code, une telle représentation est impossible. Nous sommes obligés d'arrondir à un nombre entier de bits et d'envoyer une moyenne de 1 bit.

... Mais si nous envoyons plusieurs messages en même temps, il s'avère que nous pouvons faire mieux. Considérons la transmission de deux événements de cette distribution. Si nous les envoyions indépendamment, nous devions envoyer deux bits. Comment pouvons-nous améliorer cela?



Dans la moitié des cas, nous devons envoyer $$$aa$ , dans 21% des cas - $$$ab$ ou $$$ba$ , et dans 8% des cas - $$$bb$ . Encore une fois, un code idéal comprend des bits fractionnaires.



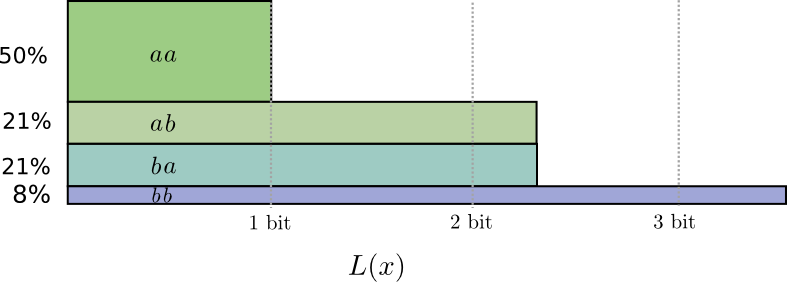
Si nous arrondissons la longueur des mots de code, nous obtenons quelque chose comme ceci:



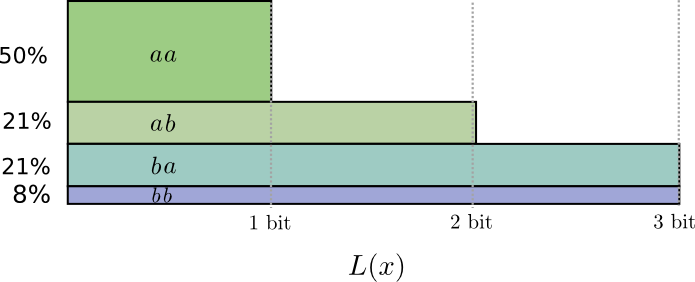
Ces codes nous donnent une longueur moyenne de message de 1,8 bits. C'est moins de 2 bits lorsque nous envoyons des messages indépendamment. C'est-à-dire dans ce cas, nous envoyons en moyenne 0,9 bit pour chaque événement. Si nous envoyions plus d'événements à la fois, la moyenne serait encore moins. À $$$n$ tendant vers l'infini, la surcharge associée à l'arrondi de notre code disparaîtra et le nombre de bits par mot de code convergera vers l'entropie.

Ensuite, notez que la longueur de mot de code idéale pour l'événement $$$a$ était de 0,5 bit, et la longueur idéale pour le mot de code $$$aa$ - 1 bit. Les longueurs de mots de code idéales s'additionnent, même si elles sont fractionnaires! Donc, si nous rapportons plusieurs événements à la fois, les longueurs s'additionneront.

Comme nous pouvons le voir, il existe une véritable signification pour les nombres fractionnaires de bits d'information, même si les codes réels ne peuvent utiliser que des entiers.

(En pratique, les gens utilisent certains schémas de codage qui sont efficaces dans différents cas. Le code Huffman, qui est en fait le type de code que nous avons esquissé ici, ne gère pas les bits fractionnaires de manière très élégante - vous devez grouper les caractères comme nous l'avons fait ci-dessus, ou utiliser des astuces plus complexes pour se rapprocher de la limite de l'entropie.Le codage arithmétique est légèrement différent, il traite avec élégance les bits fractionnaires pour être asymptotiquement optimal.)

Conclusion

Si nous sommes préoccupés par le transfert d'informations pour le nombre minimum de bits, alors ces idées sont, bien sûr, fondamentales. Si nous nous soucions de la compression des données, la théorie de l'information résout les principaux problèmes et nous donne des abstractions fondamentalement correctes. Mais que faire si on s'en fout - n'est-ce pas exotique?

Les idées de la théorie de l'information apparaissent dans de nombreux contextes: l'apprentissage automatique, la physique quantique, la génétique, la thermodynamique et même le jeu. Les praticiens de ces domaines ne se soucient pas de la théorie de l'information car ils veulent compresser les informations. Ils se soucient qu'il ait un lien irrésistible avec leur région. L'intrication quantique peut être décrite par entropie. De nombreux résultats en mécanique statistique et thermodynamique peuvent être obtenus en supposant une entropie maximale sur des choses que vous ne connaissez pas. Les gains et les pertes des joueurs sont directement liés à la divergence de KL, en particulier aux configurations itérées.

La théorie de l'information apparaît dans tous ces lieux car elle offre des formalisations concrètes et fondamentales pour beaucoup de choses que nous devons exprimer. Il nous donne des moyens de mesurer et d'exprimer l'incertitude, à quel point les deux ensembles de croyances sont différents et que la réponse à une question nous renseigne sur l'autre: la dispersion de la probabilité, la distance entre les distributions de probabilité et la dépendance des deux variables. Y a-t-il des idées alternatives et similaires? Bien sûr. Mais les idées de la théorie de l'information sont pures, elles ont vraiment de bonnes propriétés et sont basées sur des principes. Dans certains cas, ces idées sont exactement ce dont vous avez besoin, et dans d'autres cas, elles sont un médiateur pratique dans un monde chaotique.

L'apprentissage automatique est ce que je connais le mieux, alors parlons-en une minute. La classification est un type de tâche très courant dans l'apprentissage automatique. Supposons que nous voulons regarder une photo et prédire si ce sera une photo d'un chien ou d'un chat. Notre modèle peut dire quelque chose comme: "Il y a une probabilité de 80% qu'il s'agisse d'une image d'un chien, et une probabilité de 20% qu'il s'agisse d'un chat." Supposons que la bonne réponse soit un chien - quelle est la qualité de ce que nous avons dit la probabilité de Qu'est-ce qu'un chien à 80%?

C'est une question importante car nous avons besoin d'une idée de la qualité de notre modèle afin de l'optimiser pour réussir. Que devons-nous optimiser? La bonne réponse dépend en fait de la raison pour laquelle nous utilisons le modèle: nous soucions-nous seulement de savoir si notre supposition était correcte, ou nous soucions-nous de la confiance que nous avons dans la bonne réponse?À quel point est-ce mal de se tromper en toute confiance? Il n'y a pas de réponse correcte unique à cela. Et souvent, il est impossible de trouver la bonne réponse, car nous ne savons pas exactement comment le modèle sera utilisé pour formaliser ce qui nous excite finalement. Il y a des situations où l'entropie croisée est exactement ce qui nous inquiète, mais ce n'est pas toujours le cas. Plus souvent, nous ne savons pas exactement ce qui nous inquiète, et l'entropie croisée est un très bon proxy.

L'information nous donne une nouvelle base solide pour penser le monde. Parfois, il est idéal pour une tâche donnée; dans d'autres cas, pas tout à fait, mais toujours extrêmement utile. Cet essai n'a fait qu'effleurer la surface de la théorie de l'information - il y a des sujets principaux, tels que les codes de correction d'erreurs, que nous n'avons pas abordés du tout, mais j'espère avoir montré que la théorie de l'information est un merveilleux sujet qui ne devrait pas être intimidant.