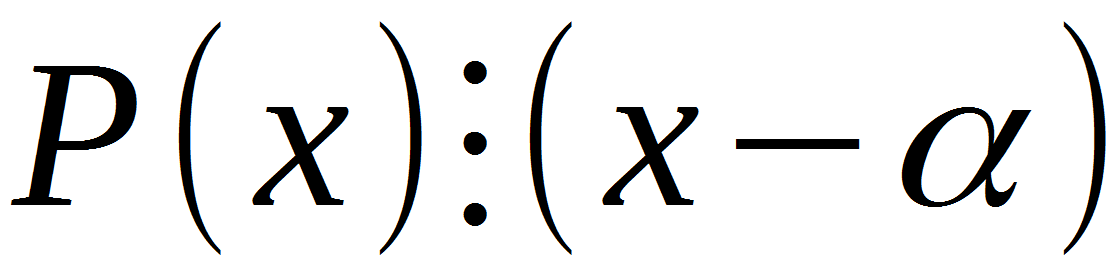
En règle générale, en physique, en informatique et en économie, nous sommes confrontés aux équations rationnelles linéaires ou fractionnaires les plus simples, moins souvent aux équations quadratiques. Et qu'en est-il des équations du troisième et du quatrième degré? Si vous êtes intéressé, alors je demande un chat.
Considérons d'abord le concept d'une équation du plus haut degré. Une équation du plus haut degré est une équation de la forme:

Dans cet article, je considérerai:
1. Équations cubiques.
2. Cubes consignés.
3. Application du schéma de Horner et du théorème de Bezout.
4. Équations biquadratiques retournables.
Équations cubiques
Les équations cubiques sont des équations dans lesquelles le degré inconnu est inconnu pour le terme senior. Les équations cubiques ont la forme suivante:

De telles équations peuvent être résolues de différentes manières, cependant, nous utiliserons les connaissances de l'école de base et résoudrons l'équation cubique par la méthode de regroupement:

Dans cet exemple, la méthode de regroupement est utilisée, nous groupons les deux premiers et les deux derniers membres, obtenant des parenthèses égales, encore une fois nous établissons, obtenant l'équation de deux parenthèses.
Le produit est alors égal à zéro, et seulement si au moins un des facteurs est égal à zéro, sur la base de cela, nous égalons chaque facteur (parenthèse) à zéro, obtenant une équation quadratique et linéaire incomplète.
Il convient également de noter que le nombre maximal de racines d'une équation égale au degré inconnu avec le terme principal, donc dans une équation cubique, il ne peut y avoir plus de trois racines, dans une biquadratique (4e degré) pas plus de quatre racines et. etc.
Retourner des équations cubiques
Les équations cubiques de retour ont la forme:

Ils sont appelés retournables car les coefficients seront reflétés. Des équations similaires sont également résolues par des méthodes scolaires, mais un peu plus délicates:

Tout d'abord, le regroupement est effectué, puis en utilisant les formules de multiplication abrégée, nous décomposons les facteurs résultants. Encore une fois, nous obtenons 2 parenthèses égales, «nous les retirons». Nous obtenons deux facteurs (crochets) et les résolvons comme deux équations différentes.
Théorème de Bezout et schéma de Horner
Le théorème de Bezout a été découvert, de manière surprenante, par Etienne Bezout, un mathématicien français qui était principalement concerné par l'algèbre. Le théorème de Bezout peut être formulé comme suit:

Voyons cela. P (x) est tout polynôme en x, (x - a) est le binôme dans lequel a est l'une des racines de l'équation que l'on trouve parmi les diviseurs du terme libre.
Trois points, il s'agit d'un opérateur indiquant qu'une expression est divisée par une autre. Il en résulte qu'ayant trouvé au moins une racine d'une équation donnée, on peut lui appliquer ce théorème. Mais pourquoi ce théorème est-il nécessaire, quel est son effet? Le théorème de Bezout est un outil universel si vous voulez abaisser le degré d'un polynôme. Par exemple, avec son aide, l'équation cubique peut être transformée en carré, biquadratique, cubique, etc.
Mais c'est une chose à comprendre, mais comment diviser? Bien sûr, vous pouvez le diviser en colonne, mais cette méthode n'est pas disponible pour tout le monde et la probabilité de faire une erreur est très élevée. Par conséquent, il existe un autre moyen, c'est le schéma de Horner. Je vais expliquer son travail avec un exemple. Supposons:

Et donc, on nous a donné un polynôme, et nous avons peut-être trouvé une des racines à l'avance. Maintenant, nous dessinons une petite plaque de 6 colonnes et 2 lignes, dans chaque colonne de la première ligne (sauf la première), nous introduisons les coefficients de l'équation. Et dans la première colonne de la ligne 2, nous ajoutons la valeur de a (la racine trouvée). Ensuite, le premier coefficient, dans notre cas 5, nous venons de souffler. Les valeurs des colonnes suivantes sont calculées comme suit:

(La photo est empruntée
ici )
Ensuite, nous faisons de même avec le reste des colonnes. La valeur de la dernière colonne (2 lignes) sera le reste de la division, dans notre cas 0, si vous obtenez un nombre différent de 0, alors vous devez choisir une approche différente. Un exemple pour une équation cubique:

Équations biquadratiques retournables
Nous avons également considéré les équations cubiques de retour ci-dessus, et maintenant nous analysons les équations biquadratiques. Leur vision générale:

Contrairement à l'équation de retour cubique, tout le monde n'a pas une paire biquadratique par rapport aux coefficients, mais sinon ils sont très similaires. Voici l'algorithme pour résoudre de telles équations:

Comme vous pouvez le voir, résoudre de telles équations n'est pas du tout simple. Mais je distinguerai ce cas de toute façon. La solution commence par diviser l'équation entière par x ^ 2. Ensuite, nous nous regroupons, ici j'ai spécifiquement introduit une ligne supplémentaire pour plus de clarté. Après cela, nous faisons l'astuce et mettons la première tranche 2, que nous ajoutons d'abord, puis soustrayons, le montant ne changera pas de toute façon, mais maintenant nous pouvons plier cette parenthèse dans le carré de la somme.
Nous supprimons -2 du crochet, en le multipliant d'abord par a, après quoi nous introduisons une nouvelle variable, t et obtenons l'équation quadratique.
Passons maintenant à un exemple:

La partie principale, comme dans l'algorithme généralisé, est divisée par x ^ 2, groupée, réduite en un carré complet, nous effectuons une substitution de variable et résolvons l'équation quadratique. Après cela, nous substituons les racines obtenues et résolvons 2 équations quadratiques supplémentaires (multipliées par x).
Champ d'application
En raison de leur encombrement et de leur spécificité, les équations de degrés supérieurs trouvent rarement leur application. Cependant, il existe encore des exemples, l'équation de Poisson pour les processus adiabatiques en physique.
Conclusion
Dans cet article, je n'ai considéré que les équations cubiques et biquadratiques. Cependant, le théorème de Bezout considéré (et le schéma de Horner) peut également être utilisé pour résoudre des équations de 5, 6, 7 et d'autres degrés, même si leur application est limitée.