À la veille du prochain lancement du cours Algorithms for Developers, nous avons organisé une leçon ouverte . Nous avons parlé de l'idée bien connue d'un arbre de segments, discuté de la façon de le construire, de le mettre à jour et rapidement O(log n) calculer la somme des nombres de n'importe quel segment d'un tableau donné. L'algorithme est très simple et économique: vous avez besoin de mémoire O(n) . Pour consolider le matériau, ils ont résolu le problème des olympiades.
Le webinaire a été dirigé par un programmeur et enseignant expérimenté, ainsi que par le responsable du cours "Algorithmes pour les développeurs"
Evgeny Volosatov .
Le dicton
L'arbre de segments est une structure de données qui permet à un algorithme simple et logarithmiquement rapide de trouver la somme des éléments d'un tableau sur un segment donné.
Par exemple, imaginez que vous devez trouver la somme des nombres suivants:

De plus, nous devons non seulement calculer la somme des nombres de la séquence spécifiée (la somme des éléments d'un certain tableau), mais
aussi rapidement que
possible pour trouver la somme de toute séquence de ces nombres . Autrement dit, nous pouvons demander un intervalle (segment) et donner la réponse le plus rapidement possible, quelle est la somme des nombres de cet intervalle:

Qu'est-ce que cela signifie rapidement? Cela signifie
plus rapidement que si nous additionnions simplement les chiffres . Après tout, il peut y avoir des millions et des milliards de chiffres ...
C'est le désir de trouver rapidement la somme des éléments consécutifs qui est devenu la motivation de notre webinaire. De plus, nous parlons non seulement de la somme, mais aussi d'autres tâches, par exemple, le calcul de toute fonction associative. Ainsi, nous parlons d'opérations dont l'exécution ne dépend pas de l'ordre de calcul.
Revenons à notre ligne:

Évidemment, si nous voulons trouver le résultat rapidement, nous devons calculer certains montants à l'avance. La première chose qui me vient à l'esprit est le pliage par deux:

Maintenant, si vous avez besoin de trouver la somme des nombres, nous pouvons le faire presque instantanément. Par exemple, pour trouver la somme du segment mentionné ci-dessus, il suffira d'ajouter 13 à 9. Tout est élémentaire: pour trouver la
somme de quatre nombres, nous en avons ajouté
seulement deux .
Nous compliquons la tâche:
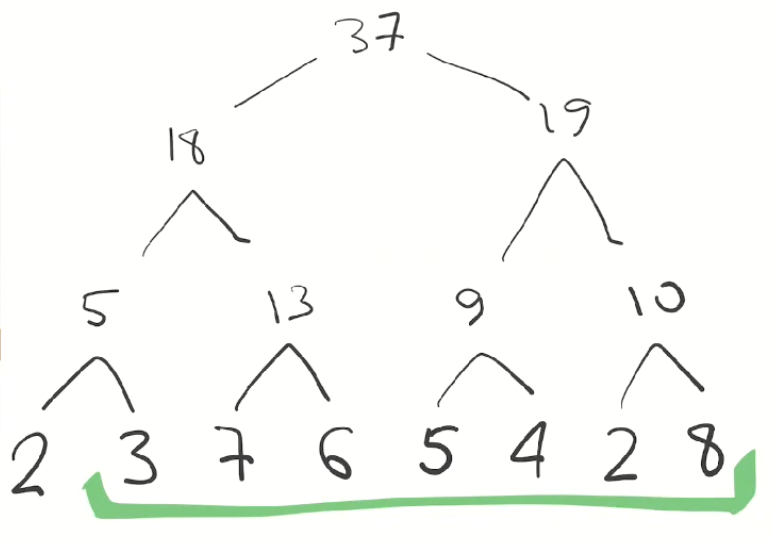
Pour trouver la somme de ce segment, nous devons additionner les éléments qui, d'une manière ou d'une autre, couvrent notre segment:

Bien sûr, 3 + 13 + 19 = 35. Notez que pour trouver la
somme des sept nombres , nous en avons ajouté
seulement trois . Si le segment était composé de mille éléments, il suffirait d'ajouter en moyenne 10 éléments, puisque nous avons une complexité logarithmique avec un logarithme en base 2. Et c'est rapide!
Arbre binaire complet
Un arbre binaire complet est un arbre dont chaque élément a exactement deux enfants.
Pour travailler avec un arbre binaire complet, vous pouvez et devez utiliser une structure de données telle qu'un tableau.
La numérotation de ce tableau est pratique à partir d'un . Nous numérotons chaque élément de l'arbre binaire avec des nombres naturels de 1 à 2
n -1:

Toute la beauté de l'approche est qu'il est très facile de calculer le nombre d'enfants et de parents.
La formule pour calculer "l'enfant gauche":
i * 2 , la "droite":
i * 2 + 1 .

Par exemple, nous calculons le nombre d'enfants dans le cinquième élément:
- 5 x 2 = 10 ;
- 5 x 2 + 1 = 11 .
Et comment passer de «l'enfant» au «parent»? Nous utilisons la
division entière i / 2Ok, et comment déterminer si l'enfant est à gauche ou à droite? La réponse est la suivante: les
enfants de gauche ont des nombres pairs, les enfants de droite ont des nombres impairs .
Rappelez-vous ces points.
Revenant à notre exemple d'arbre binaire, nous nous demandons, comment pouvons-nous le construire? Regardez, nous avons d'abord un tableau de nombres:

Pour cela, vous devez construire un arbre binaire. Quelle quantité de mémoire est nécessaire pour stocker l'arbre binaire, au fond duquel se trouvent ces éléments?
La réponse à cette question est
2n si
n est une puissance de deux.
Nous allons plus loin, car deux autres questions se posent à nous:
- à partir de quel élément avez-vous besoin de placer les numéros sources dans un tableau d'un arbre binaire complet?
- à partir de quel élément et dans quelle direction allons-nous commencer à remplir notre arbre de quantités pré-calculées?

La réponse à la première question est assez simple: nous avons 8 éléments, au total il y aura 16 éléments dans le tableau, ce qui signifie que le premier élément sera numéroté 16 - 8 = 8. Et nous commencerons à construire de gauche à droite et de bas en haut, à partir de l'élément 7, additionner des valeurs chez les enfants, comme ceci:

Ensuite, vous devez déterminer comment trouver la somme du segment souhaité. Revenons à notre premier exemple, numérotons les éléments et définissons un segment, et nous désignons le premier élément du segment à ajouter par la lettre L, et le dernier par R:

Il faut maintenant introduire un concept de plus pour que l'algorithme des actions soit clair. Nous parlons du concept des éléments fondamentaux et de leurs segments fondamentaux correspondants. L'élément fondamental est tout élément de l'ensemble du tableau, et le segment fondamental lui correspond, c'est-à-dire les éléments du tableau initial qui sont ses enfants / petits-enfants immédiats. Pour l'élément fondamental avec le numéro 4 «5», le segment fondamental sera de 8 à 9 élément: [«2»; «3»]:

Quant à l'élément fondamental avec le nombre 10 - «7» (nous l'avons désigné L), il coïncide avec son segment fondamental. Est-il possible d'élargir ce segment fondamental sans dépasser LR? Dans notre cas, vous le pouvez. La règle pour la bordure gauche est la suivante: s'il s'agit d'un enfant gauche, alors le segment fondamental peut être développé, le nouvel élément fondamental sera le parent de l'actuel. Autrement dit, nous pouvons écrire ce qui suit dans le programme:

Passons maintenant à l'élément droit R. C'est un élément fondamental et un enfant gauche, donc nous ne pouvons plus étendre la zone (nous allons dépasser le segment). Nous pouvons donc ajouter cet élément à la réponse:

Ensuite, vous avez besoin de l'élément gauche pour vous déplacer vers la droite et de la droite vers la gauche. Pour l'élément gauche d'index L = 10, l'index suivant est 5, car il ira au parent. Mais il ira d'abord vers la droite, puis vers le haut:

Ainsi, la valeur de L est passée à un niveau supérieur et un peu à droite. Comment R diminuera-t-il? En utilisant la formule (R - 1) / 2.

Voici un tel algorithme. Quant aux valeurs suivantes des variables L et R, elles seront déplacées comme suit:

S'il n'y a pas 8 éléments dans l'arbre, mais un nombre incommode, disons 12, nous devrons ajouter l'arbre (l'arbre binaire doit être complet) à 16.
La formule de calcul du nombre d'éléments (toute la partie du logarithme est prise):

Maintenant, nous calculons la fonction associative de trouver le
minimum . Voici notre arbre et coupé:

Combien de fois pensez-vous que l'élément 5 sera impliqué dans notre fonction - une ou deux? Bien sûr, un, mais comment cela est-il vérifié dans l'algorithme? En fait, cet élément est soit un fils gauche ou un fils droit, ce qui signifie que l'action sera effectuée pour L ou R.
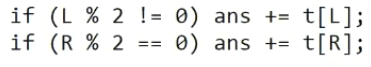
+
Considérez maintenant l'opération de modification. Supposons qu'un élément ait changé, par exemple, au lieu de 7, 0 est entré. Pour que notre arborescence de segments reste en état de fonctionnement, nous devons mettre à jour tous les parents, et nous devons aller tout en haut.

Solution du problème des olympiades
L'une des exigences de ces tâches est que tout fonctionne rapidement. Nous avons donc la condition suivante:

Nous allons le résoudre en utilisant la connaissance de l'arbre des segments. En conséquence, nous obtenons le code C # suivant:

Nous l'envoyons pour vérification, nous voyons que la
décision a été prise et est complète , ce qui signifie que notre algorithme fonctionne.

C'est tout, si vous voulez plus de détails,
regardez l'intégralité de la vidéo . Vous pouvez également lire à loisir les articles d’auteurs suivants de notre professeur
Evgeny Volosatov sur Habré:
-
Équilibrage des arbres rouge-noir - Trois cas ;
-
Le cheval se déplace sur des mors. Bitboard d'échecs .