Tout au long de la géographie: navigation et tâches géodésiques dans différentes langues

Salutations, très chers!

"... le véritable emplacement du navire, bien qu'inconnu, n'est pas accidentel, il l'est, mais il est inconnu à quel moment" V. Aleksishin et al. Practical Navigation, 2006. p. 71

«Les piétons sont sortis des deux bords de la galaxie ...» (C) Sergey Popov (astrophysicien)

À la lumière des nouvelles tendances du style Art nouveau, j'ai voulu écrire sur la résolution des problèmes géodésiques sur terrain plat. Mais jusqu'à présent, l'affirmation selon laquelle la forme de la terre est commodément approximée par un ellipsoïde n'est pas une hérésie et une sédition, j'invite tous ceux qui sont intéressés à rejoindre les modèles les plus conservateurs.

• distance entre deux points géographiques
• détermination d'un point par sa distance connue et l'angle azimutal
• détermination de la position d'un point par des distances mesurées à des points connus (TOA, TOF)
• détermination de la position d'un point par des temps d'arrivée de signal mesurés (TDOA)

Tout cela en C #, Rust et Matlab, sur la sphère et les ellipsoïdes, avec des images, des graphiques, du code source - sous la coupe.

Et cela, le KDPV pertinent:



Pour ceux qui sont pressés (je le suis moi-même), voici le référentiel sur GitHub , où se trouvent tous les codes sources avec des tests et des exemples.

Le référentiel est organisé très simplement: la bibliothèque est actuellement présentée en trois langues et chaque implémentation est dans son propre dossier:

• C #
• Rouille
• Matlab

L'implémentation la plus complète en C #: contrairement aux autres, il contient des soi-disant méthodes base longue virtuelle - c'est quand un objet dont la position que vous devez déterminer est stationnaire, et il y a des distances mesurées à partir de différents points, avec une position connue.

Pour voir comment tout fonctionne, avec quels paramètres il appelle et ce qui revient, et effectuer des reconnaissances au combat, il existe différentes démos et tests:

• Tester l' application console en C #
• Testez toute la bibliothèque sur Matlab
• Script de démonstration TOA / TDOA avec de belles images sur Matlab
• Script sur Matlab pour comparer la précision des solutions aux problèmes géodésiques sur une sphère (équations de Haversine) et sur un ellipsoïde (équations de Vincenty)
• Pour l' implémentation sur Rust , le code de la bibliothèque contient des tests. Et vous pouvez voir comment tout fonctionne simplement en exécutant la commande «Cargo -test»

J'ai essayé de rendre la bibliothèque aussi indépendante et autonome que possible. De sorte que si vous le souhaitez, vous pouvez simplement prendre la pièce souhaitée (en vous référant à la source, bien sûr), sans faire glisser tout le reste.

Les angles sont presque toujours en radians, les distances en mètres, le temps en secondes.

Maintenant, commençons par le début:

Tâches d'arpentage

Il existe deux tâches géodésiques typiques: directe et inverse.

Si par exemple, je connais mes coordonnées actuelles (latitude et longitude), puis j'ai parcouru 1000 kilomètres strictement vers le nord-est, bien ou vers le nord. Quelles coordonnées vais-je avoir maintenant? - Découvrir les coordonnées que je vais avoir, c'est résoudre un problème géodésique direct.

C'est-à-dire: Une tâche géodésique directe consiste à trouver les coordonnées d'un point par une distance connue et un angle de direction.

Avec le problème inverse, tout est complètement clair - par exemple, j'ai déterminé mes coordonnées, puis j'ai marché pendant un certain temps en ligne droite et j'ai à nouveau déterminé mes coordonnées. Trouver combien je suis allé signifie résoudre le problème de la géodésique inverse.

C'est-à-dire: Le problème géodésique inverse est de trouver la distance entre deux points avec des coordonnées géographiques connues.

Vous pouvez résoudre ces problèmes de plusieurs manières, selon la précision nécessaire et le temps que vous êtes prêt à y consacrer.

Le moyen le plus simple est d'imaginer que la terre est plate - c'est une sphère. Essayons.
Voici la formule pour résoudre le problème direct ( source ):

$$

$$\ phi_2 = arcsin (sin \ phi_1cos \ delta + cos \ phi_1sin \ delta cos \ theta)$$

$$

$$\ lambda_2 = \ lambda_1 + atan2 (sin \ theta sin \ delta cos \ phi_1, cos \ delta-sin \ phi_1sin \ phi_2)$$

Ici $$$\ phi_1$, $$$\ lambda_1$- latitude et longitude du point de départ, $$$\ theta$- angle directionnel, mesuré dans le sens horaire à partir de la direction nord (vu de dessus), $$$\ delta$- distance angulaire d / R. d est la distance mesurée (parcourue) et R est le rayon de la terre. $$$\ phi_2$, $$$\ lambda_2$- latitude et longitude du point souhaité (celui auquel nous sommes arrivés).

Pour résoudre le problème inverse, il en existe une autre (formule non moins simple):

$$

$$a = sin ^ 2 (\ Delta \ phi / 2) + cos \ phi_1 cos \ phi_2 sin ^ 2 (\ Delta \ lambda / 2)$$

$$

$$d = R * atan2 (\ sqrt a, \ sqrt {1-a})$$

O Where $$$\ phi_1$, $$$\ lambda_1$et $$$\ phi_2$, $$$\ lambda_2$- coordonnées des points, R - rayon terrestre.

Les formules décrites sont appelées équations de Haversine.

• Dans une implémentation C #, les fonctions correspondantes sont appelées HaversineDirect et HaversineInverse et vivent dans Algorithms.cs .
• Dans une implémentation Rust, ce sont les fonctions haversine_direct et haversine_inverse .
• Enfin, sur Matlab, les fonctions sont stockées dans des fichiers séparés, et voici les deux fonctions:
  HaversineDirect et HaversineInverse

Pour C #, je fournirai les noms des fonctions et un lien vers le fichier où elles se trouvent. Pour Rust - seuls les noms des fonctions (puisque la bibliothèque entière est dans un fichier), et pour Matlab - un lien vers le fichier de script correspondant, car dans Matlab il y a une fonction - un script.

Évidemment, il y a une sorte de prise: la terre n'est pas une sphère, mais un plan, et cela doit en quelque sorte affecter l'applicabilité de ces formules et / ou la précision de la solution.

Et vraiment. Mais pour le déterminer, vous devez comparer avec quelque chose.
En 1975, Thaddeus Vincenty a publié une solution efficace sur le plan des calculs de problèmes géodésiques directs et inverses à la surface d'un sphéroïde (mieux connu sous le nom d' Ellipsoïde de la Révolution, camarade! Ellisoid of Rotation), qui est devenu presque standard.

La description du dispositif de la méthode est dessinée dans un article séparé, donc je me limiterai seulement à envoyer au travail original de Vincenti et à une calculatrice en ligne avec une description de l'algorithme.

Dans la bibliothèque UCNLNav, la solution des problèmes géodésiques directs et inverses à l'aide des formules Vincenti réside dans les fonctions suivantes:

• C #: VincentyDirect et VincentyInverse dans Algorithms.cs .
• Rouille: vincenty_inverse et vincenty_direct
• Matlab: Nav_vincenty_direct et Nav_vincenty_inverse .

Parce que La solution de Vincenti est itérative, puis le nombre maximum d'itérations (it_limit) est présent dans la liste des paramètres, et le nombre réel d'itérations est dans la liste des résultats. Il existe également un seuil spécifiant une condition d'arrêt (epsilon). Dans la plupart des cas, pas plus de 10 itérations sont nécessaires, mais pour les points presque antipodes (tels que les pôles nord et sud), la méthode converge mal, et jusqu'à 2000 itérations peuvent être nécessaires.

La différence la plus importante est que ces formules exécutent la solution sur un sphéroïde et que ses paramètres doivent être transférés aux fonctions. Il existe une structure simple pour cela qui le décrit.

Dans toutes les implémentations, l'un des ellipsoïdes standard peut être obtenu sur une seule ligne. (Très souvent, WGS84 [https://en.wikipedia.org/wiki/World_Geodetic_System] est utilisé et nous le donnerons comme exemple):

• En C #: Algorithms.cs a un champ statique Algorithms.WGS84Ellipsoid - il peut être transmis aux méthodes.
• Sur la rouille:

  let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); 

• Sur Matlab:

   el = Nav_build_standard_ellipsoid('WGS84'); 

Le nom des paramètres restants est assez évident et ne devrait pas créer d'ambiguïtés.

Afin de comprendre ce qu'il nous en coûtera d'utiliser des solutions pour une sphère au lieu d'une ellipse, il existe un script sur l'implémentation de Matlab.

Matlab est incroyablement pratique pour afficher n'importe quoi sans gestes inutiles, donc je l'ai choisi pour la démonstration.

La logique de son script:

1. Nous prenons un point avec des coordonnées arbitraires

 sp_lat_rad = degtorad(48.527683); sp_lon_rad = degtorad(44.558815); 

et une direction arbitraire (j'ai choisi vers l'ouest):

 fwd_az_rad = 1.5 * pi + (rand * pi / 4 - pi / 8); 

2. On en passe à une distance toujours croissante. Pourquoi définissons-nous immédiatement le nombre d'étapes et la taille des étapes:

 n_samples = 10000; step_m = 1000; % meters distances = (1:n_samples) .* step_m; 

3. Pour chaque étape, nous résolvons le problème géodésique direct sur la sphère et sur l'ellipsoïde, obtenant le point souhaité:

 [ h_lats_rad(idx), h_lons_rad(idx) ] = Nav_haversine_direct(sp_lat_rad,... sp_lon_rad,... distances(idx),... fwd_az_rad,... el.mjsa_m); [ v_lats_rad(idx), v_lons_rad(idx), v_rev_az_rad, v_its ] = Nav_vincenty_direct(sp_lat_rad,... sp_lon_rad,... fwd_az_rad,... distances(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

4. Pour chaque étape, nous résolvons des problèmes de géodésique inverse - nous calculons les distances entre les résultats obtenus sur une sphère et un ellipsoïde:

 [ v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(h_lats_rad(idx),... h_lons_rad(idx),... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

5. Nous vérifions les solutions directes inverses pour les deux méthodes:

 [ ip_v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); ip_h_dist(idx) = Nav_haversine_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el.mjsa_m); 

Dans le script, cette séquence est effectuée d'abord pour une étape = 1000 m, puis pour une étape = 1 mètre.

Voyons d'abord comment les résultats des décisions directes diffèrent en coordonnées (latitude et longitude), pour lesquelles nous calculons les vecteurs "delta", puisque tout est écrit sur Matlab sur une seule ligne:

 d_lat_deg = radtodeg(v_lats_rad - h_lats_rad); %    ( ) d_lon_deg = radtodeg(v_lons_rad - h_lons_rad); %    ( ) 

Sur l'axe, l'abscisse sera affichée sur une échelle logarithmique, car nos distances varient de 1 à 10 000 km:

 figure semilogx(distances, d_lat_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Latitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); figure semilogx(distances, d_lon_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Longitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); 

En conséquence, nous obtenons de tels graphiques pour la latitude:



Et pour la longitude:



Je ne comprends pas en degrés, je suis toujours guidé par la méthode d'estimation "à l'oeil":
1 ° de quelque chose est une moyenne de 100-110 km. Et si l'erreur est supérieure à un millionième ou au moins cent millième de degré - ce sont de mauvaises nouvelles.

Ensuite, nous regardons les distances entre le point de départ et le point obtenu à chaque étape selon les formules de la sphère et de l'ellipsoïde. Nous calculons la distance en utilisant les formules de Vincenti (car elle est évidemment plus précise - l'auteur promet une erreur en millimètres). Les graphiques en mètres et en kilomètres sont beaucoup plus tangibles et familiers:

 figure semilogx(distances, v_dist, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Endpoint difference by Vincenty)'); xlabel('Distance, m'); ylabel('Difference, m'); 

En conséquence, nous obtenons l'image suivante:



Il s'avère qu'à des portées de 10 000 km, les méthodes divergent de 10 km.

Si maintenant tout est répété pour une étape 1000 fois plus petite, c'est-à-dire lorsque toute la plage le long de l'axe X n'est pas de 10 000 km mais seulement de 10 km, l'image se présente comme suit:



C'est-à-dire qu'à une distance de 10 km, seulement 20 mètres de montée, et pour 1-2 mètres, les formules ne divergent qu'à des distances d'environ 1000 mètres.

La conclusion du capitaine est évidente: si la précision des formules avec la solution sur la sphère est suffisante pour le problème, alors nous les utilisons - elles sont plus faciles et plus rapides.

Eh bien, pour ceux pour qui la précision millimétrique ne suffit pas, en 2013 un ouvrage a été publié décrivant la solution des problèmes géodésiques avec une précision nanométrique (!). Je ne suis pas sûr de pouvoir trouver immédiatement où cela pourrait être nécessaire - sauf pour les levés géodésiques lors de la construction de détecteurs d'ondes gravitationnelles ou quelque chose de complètement fantastique).

Passons maintenant aux plus savoureux:

Résolution des problèmes de navigation

À l'heure actuelle, la bibliothèque peut déterminer:

• L'emplacement de l'objet par la distance aux points, avec des coordonnées connues en 2D et 3D. C'est ce que nous appelons TOA - Time Of Arrival (ou plus correctement, TOF - Time Of Flight)
• La localisation de l'objet par les différences d'heures d'arrivée en 2D et 3D. C'est ce que nous appelons TDOA (Time Difference Of Arrival).

En réalité, nous mesurons toujours les plages ou les heures d'arrivée d'un signal (et, par conséquent, leur différence) avec des erreurs, avec du bruit. Par conséquent, la solution des problèmes de navigation dans la grande majorité des cas est la minimisation des erreurs. La méthode des moindres carrés et c'est tout .

Ce qui doit être minimisé s'appelle la fonction résiduelle.

Pour les tâches TOA, cela ressemble à ceci:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2 )} - r_i] ^ 2$$

O Where $$$\ epsilon (x, y, z)$- la valeur de la fonction résiduelle pour un certain point avec des coordonnées $$$(x, y, z)$; N est le nombre de points de contrôle ayant des coordonnées $$$(x_i, y_i, z_i)$, $$$r_i$- distances mesurées entre les points de référence et l'objet positionné.

Et pour des tâches TDOA comme celle-ci:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1, j = 2, i \ neq j} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2+ (z-z_i) ^ 2)} - \\ \ sqrt {(x-x_j) ^ 2 + (y-y_j) ^ 2 + (z-z_j) ^ 2)} - \ nu (t_ {Ai} -t_ {Aj})] ^ 2$$

Ici, tout est pareil, seules les paires de points de référence et les heures d'arrivée correspondantes sont prises en compte $$$t_ {Ai}$et $$$t_ {Aj}$et $$$\ nu$- vitesse de propagation du signal.

Et donc ces fonctions regardent dans le code:




Comme vous pouvez le voir, les deux fonctions fonctionnent avec un nombre variable de points de contrôle ou de lignes. En général, les tâches peuvent être différentes et les fonctions résiduelles aussi.

Par exemple, vous pouvez résoudre le problème non seulement de déterminer l'emplacement, mais également de déterminer l'orientation. Dans ce cas, la fonction résiduelle contiendra un ou plusieurs angles.

Arrêtons-nous plus en détail sur la structure interne de la bibliothèque

À ce stade, la bibliothèque fonctionne avec des tâches 2D et 3D et le solveur lui-même ne sait pas et ne veut pas savoir à quoi ressemble la fonctionnalité minimisée. Ceci est réalisé de la manière suivante.

Le solveur a deux aspects: les solveurs 2D et 3D basés sur la méthode Nelder-Mead ou, comme on l'appelle également, la méthode Simplex.

Puisque cette méthode ne nécessite pas le calcul de dérivées (la minimisation dite sans dérivé ), idéalement, l'utilisateur de la bibliothèque peut utiliser ses propres fonctions résiduelles si nécessaire. De plus, en théorie, il n'y a pas de limite supérieure sur le nombre de points de contrôle utilisés pour résoudre le problème.

En C # et Rust, les solveurs 2D et 3D sont des méthodes génériques:

 public static void NLM2D_Solve<T>(Func<T[], double, double, double, double> eps, T[] baseElements,... //       : fxi[0] = eps(baseElements, xix[0], xiy[0], z); 

Un exemple d'appel du solveur lui-même:

 public static void TOA_NLM2D_Solve(TOABasePoint[] basePoints, double xPrev, double yPrev, double z, int maxIterations, double precisionThreshold, double simplexSize, out double xBest, out double yBest, out double radialError, out int itCnt) { NLM2D_Solve<TOABasePoint>(Eps_TOA3D, basePoints, xPrev, yPrev, z, maxIterations, precisionThreshold, simplexSize, out xBest, out yBest, out radialError, out itCnt); } 

Sur la rouille ...

 pub fn nlm_2d_solve<T>(eps: Eps3dFunc<T>, base_elements: &Vec<T>... 

Tout est identique, fidèle à la syntaxe de la langue.

À Matlabe, avec le volontarisme inhérent, le solveur lui-même n'a aucune idée des éléments de base qui lui sont transmis - l'utilisateur lui-même doit s'assurer que le lien vers la fonction résiduelle et l'ensemble des éléments de support transmis au solveur sont compatibles:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(eps, base_elements, .... 

Et en conséquence, l'appel au solveur ressemble à ceci:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size) [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(@Nav_eps_toa3d, base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size); end 

Il existe un script Matlab spécial pour illustrer la solution des problèmes TOA et TDOA.

La démonstration en 2D n'a pas été choisie par hasard - je ne suis pas sûr de savoir comment afficher la fonction résiduelle tridimensionnelle de manière simple et informative =)

Alors. Au début du script, certains paramètres peuvent être modifiés:

 %% parameters n_base_points = 4; %    area_width_m = 1000; %   max_depth_m = 100; %   ( Z) propagation_velocity = 1500;%     -  max_iterations = 2000; %    precision_threshold = 1E-9; %   simplex_size = 1; %      contour_levels = 32; %      range_measurements_error = 0.01; % 0.01 means 1% of corresponding slant range %    -   1% 

La position du point souhaité est définie de manière aléatoire dans la zone spécifiée:

 %% actual target location r_ = rand * area_width_m / 2; az_ = rand * 2 * pi; actual_target_x = r_ * cos(az_); actual_target_y = r_ * sin(az_); actual_target_z = rand * max_depth_m; 

Ensuite, placez au hasard les points de contrôle, calculez la distance entre les points souhaités et affichez tout:

 %% base points figure hold on grid on base_points = zeros(n_base_points, 4); for n = 1:n_base_points r_ = area_width_m / 2 - rand * area_width_m / 4; az_ = (n - 1) * 2 * pi / n_base_points; base_x = r_ * cos(az_); base_y = r_ * sin(az_); base_z = rand * max_depth_m; dist_to_target = Nav_dist_3d(base_x, base_y, base_z, actual_target_x, actual_target_y, actual_target_z); base_points(n, :) = [ base_x base_y base_z dist_to_target ]; end N =1:n_base_points; plot3(actual_target_x, actual_target_y, actual_target_z,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot3(base_points(N, 1), base_points(N, 2), base_points(N, 3),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); for n = 1:n_base_points line([ actual_target_x, base_points(n, 1) ], [ actual_target_y, base_points(n, 2) ], [ actual_target_z, base_points(n, 3) ]); end view(45, 15); legend('target', 'base points'); title('Placement of base stations and the target'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); zlabel('Z coordinate, m'); 

En conséquence, nous obtenons l'image suivante:



Ajoutez des erreurs aléatoires aux mesures de distance:

 % adding range measurement errors base_points(N, 4) = base_points(N, 4) + base_points(N, 4) *... (rand * range_measurements_error - range_measurements_error / 2); 

Nous construisons la fonction résiduelle pour la région sélectionnée avec une certaine décimation - sinon, les calculs peuvent prendre un temps considérable. J'ai choisi la taille de la zone 1000 x 1000 mètres et je considère la fonction résiduelle dans toute la zone après 10 mètres:

 % error surface tiles tile_size_m = 10; n_tiles = area_width_m / tile_size_m; %% TOA solution error_surface_toa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_toa(t_x, t_y) = Nav_eps_toa3d(base_points,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf_a = [1:n_tiles] * tile_size_m - area_width_m / 2; surf(surf_a, surf_a, error_surface_toa); title('TOA solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

Voici la fonction résiduelle:



Bien sûr, j'étais un peu rusé - les positions relatives des points de contrôle et celles souhaitées sont choisies de sorte qu'elles forment toujours une figure convexe avec le point souhaité à l'intérieur. En grande partie à cause de cela, la surface a un minimum, ce qui est sans aucun problème.

Un lecteur arrogant peut changer cet ordre de choses et essayer de définir les points d'ancrage et celui souhaité par accident.

Maintenant, affichez-les tous ensemble. Cela est difficile à faire en surface - différentes valeurs le long de l'axe vertical. Par conséquent, il est pratique de tout dessiner sur une tranche bidimensionnelle:

 figure hold on contourf(surf_a, surf_a, error_surface_toa, contour_levels); plot(actual_target_x, actual_target_y,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(base_points(N, 1), base_points(N, 2),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); [ x_prev, y_prev ] = Nav_toa_circles_1d_solve(base_points, actual_target_z, pi / 180, 10, 0.1); [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, actual_target_z,... max_iterations, precision_threshold, simplex_size); plot(x_best, y_best,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); title(sprintf('TOA Solution: Residual function. Target location estimated with E_{radial} = %.3f m in %d iterations', rerr, it_cnt)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Residual function value', 'Actual target location', 'Base points', 'Estimated target location'); 

Le résultat est quelque chose comme ceci:



L'erreur radiale est affichée dans l'en-tête du graphique - la racine de la valeur finale de la fonction résiduelle. Le graphique montre que l'emplacement réel et l'emplacement calculé sont en bon accord, mais l'échelle ne nous permet pas de déterminer dans quelle mesure.

Par conséquent, nous affichons séparément l'emplacement calculé du point souhaité et son emplacement réel et calculons la distance entre eux:

 figure hold on grid on dx = actual_target_x - x_best; dy = actual_target_y - y_best; plot(0, 0,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(dx, dy,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); plot(-dx * 2, -dy * 2, '.w'); plot(dx * 2, dy * 2, '.w'); d_delta = Nav_dist_3d(actual_target_x, actual_target_y, actual_target_z, x_best, y_best, actual_target_z); title(sprintf('TOA Solution: Actual vs. Estimated location, distance: %.3f m', d_delta)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Actual target location', 'Estimated target location'); 

Voici à quoi ça ressemble:



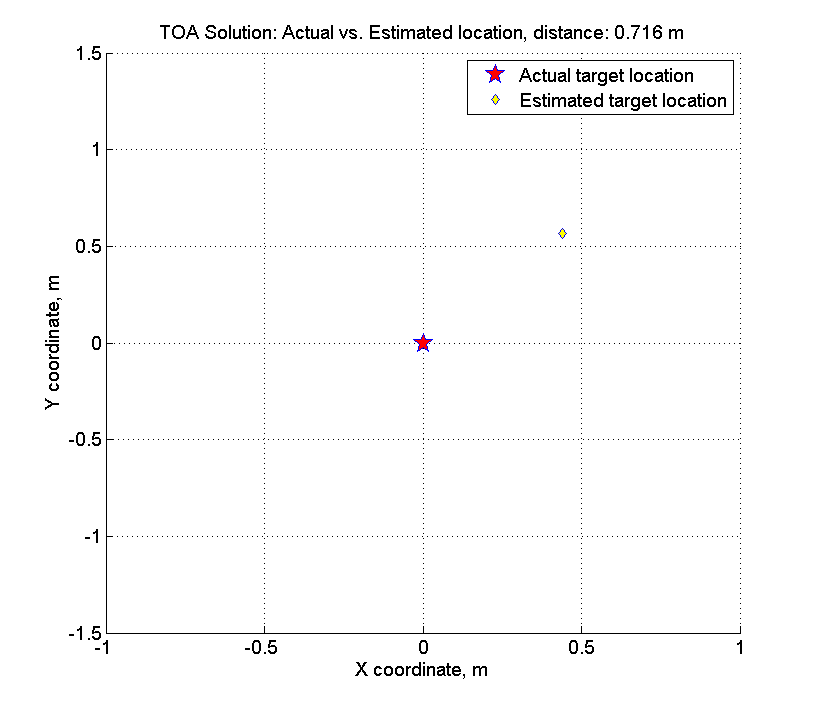
Rappelons que nous avons l'amplitude d'une erreur aléatoire - 1% de la plage, en moyenne, la plage est de ~ 200-400 mètres, c'est-à-dire l'amplitude de l'erreur est d'environ 2 à 4 mètres. Lors de la recherche d'une solution, nous avons commis une erreur de seulement 70 centimètres.

Maintenant, par analogie, nous allons essayer de résoudre le problème TDOA sur les mêmes données. Pour ce faire, nous prétendrons que nous ne connaissons que les heures d'arrivée des signaux du point souhaité aux points de référence (ou vice versa, peu importe) - nous divisons simplement nos distances par la vitesse de propagation du signal - seules leurs différences et non les valeurs absolues sont importantes.

 % since TDOA works with time difference of arriaval, % we must recalculate base point's distances to times base_points(N,4) = base_points(N,4) / propagation_velocity; base_lines = Nav_build_base_lines(base_points, propagation_velocity); 

Construisez et dessinez une surface d'erreurs:

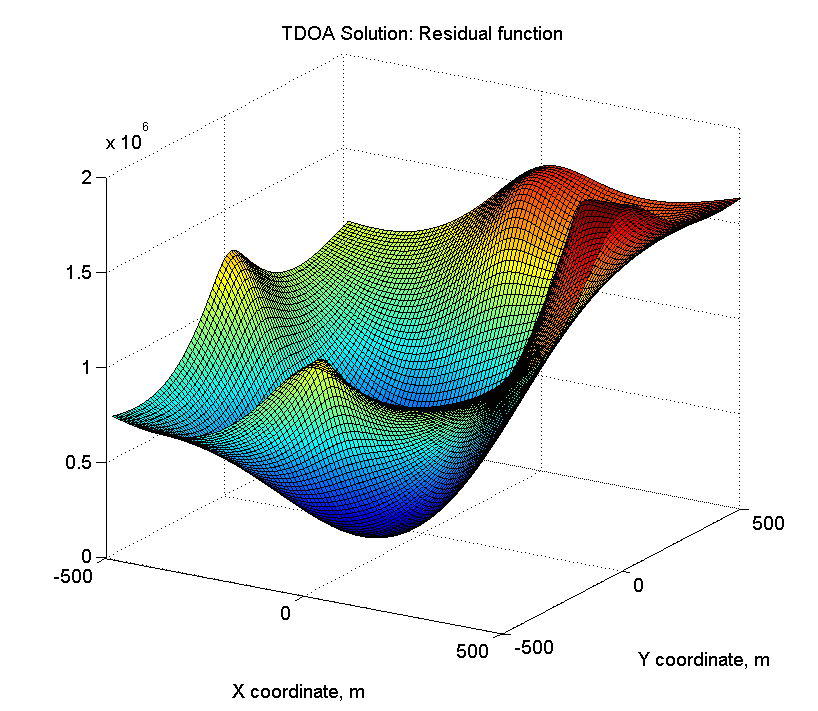
 error_surface_tdoa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_tdoa(t_x, t_y) = Nav_eps_tdoa3d(base_lines,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf(surf_a, surf_a, error_surface_tdoa); title('TDOA Solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

Il s'avère quelque chose comme ceci:



Et la vue de dessus avec les points de référence, les positions réelles et calculées du point souhaité:



Et plus en détail, l'écart entre l'emplacement réel et l'emplacement calculé:



Dans ce cas particulier, la solution TDOA s'est avérée encore meilleure que la solution TOA - l'erreur absolue est de 0,3 mètre.

Bon dans le modèle - vous savez toujours exactement où le point souhaité est réellement situé. C'est pire dans l'air - peut-être qu'il y a plusieurs points de vue, sous l'eau, vous venez de calculer quelque chose et c'est tout - dans 99% des cas, afin de calculer l'écart par rapport à l'emplacement réel, il (cet emplacement) doit également être calculé en premier.

Maintenant, en guise de conclusion, nous allons combiner nos nouvelles connaissances sur les tâches géodésiques et de navigation.

Accord final

Au plus près de la situation de la vie réelle:

• Supposons que nos points de référence disposent de récepteurs GNSS intégrés et que nous ne connaissons que leurs coordonnées géographiques
• la coordonnée verticale nous est inconnue (problème 3D)
• nous mesurons uniquement les temps d'arrivée du signal des points de référence sur le souhaité ou vice versa

Cette situation est décrite dans le test le plus récent des trois implémentations. J'ai en quelque sorte privé Rust, et j'analyserai le dernier exemple dessus.

Donc, le test le plus récent de la bibliothèque. Comme coordonnées du point souhaité, j'ai choisi un endroit dans le parc, où je me promène souvent avec le chien.

 #[test] fn test_tdoa_locate_3d() { let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); let base_number = 4; // 4   let start_base_z_m: f64 = 1.5; //  Z     let base_z_step_m = 5.0; //        5  let actual_target_lat_deg: f64 = 48.513724 // singed degrees let actual_target_lon_deg: f64 = 44.553248; // signed degrees let actual_target_z_m: f64 = 25.0; // meters - ,    ! // generate base points via Vincenty equations let mut base_points = Vec::new(); let start_dst_projection_m = 500.0; //      500  let dst_inc_step_m = 50.0; //   -  50   // azimuth step let azimuth_step_rad = PI2 / base_number as f64; //     let actual_target_lat_rad = actual_target_lat_deg.to_radians(); let actual_target_lon_rad = actual_target_lon_deg.to_radians(); // signal propagation speed let velocity_mps = 1450.0; // m/s,        //     for base_idx in 0..base_number { //        let dst_projection_m = start_dst_projection_m + dst_inc_step_m * base_idx as f64; //       let azimuth_rad = azimuth_step_rad * base_idx as f64; //        Vincenty let vd_result = vincenty_direct(actual_target_lat_rad, actual_target_lon_rad, azimuth_rad, dst_projection_m, &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); //   Z let base_z_m = start_base_z_m + base_z_step_m * base_idx as f64; //        let dz_m = actual_target_z_m - base_z_m; //      let slant_range_m = (dst_projection_m * dst_projection_m + dz_m * dz_m).sqrt(); //   .          Rust   ! base_points.push((vd_result.0.to_degrees(), vd_result.1.to_degrees(), base_z_m, slant_range_m / velocity_mps)); } //     -   NAN- let lat_prev_deg = f64::NAN; let lon_prev_deg = f64::NAN; let prev_z_m = f64::NAN; //   let tdoa_3d_result = tdoa_locate_3d(&base_points, lat_prev_deg, lon_prev_deg, prev_z_m, NLM_DEF_IT_LIMIT, NLM_DEF_PREC_THRLD, 10.0, &el, velocity_mps); //          let vi_result = vincenty_inverse(actual_target_lat_rad, actual_target_lon_rad, tdoa_3d_result.0.to_radians(), tdoa_3d_result.1.to_radians(), &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); assert!(vi_result.0 < start_dst_projection_m * 0.01, "Estimated location is farer than limit (1%): {}", vi_result.0); assert_approx_eq!(tdoa_3d_result.2, actual_target_z_m, start_dst_projection_m * 0.05); assert!(tdoa_3d_result.3 < start_dst_projection_m * 0.01, "Residual function greater than limit (1%): {}", tdoa_3d_result.3); assert!(tdoa_3d_result.4 < NLM_DEF_IT_LIMIT, "Method did not converge: iterations limit exeeded {}", tdoa_3d_result.4); } 

En conséquence, nous avons:
Localisation réelle (Lat, Lon, Z): 48.513724 44.553248 25
Position calculée (Lat, Lon, Z): 48,513726 44,553252 45,6
Distance entre les points de la surface (m): 0,389
Différence de coordonnées Z (m): 20,6

La correspondance «plan» est très bonne, l'erreur n'est que de 40 centimètres et la coordonnée verticale est de 20 mètres. Pourquoi cela se produit-il, je suggère aux lecteurs de penser =)

PS

La bibliothèque décrite est un projet purement éducatif, que j'ai l'intention de développer et de reconstituer davantage. Les plans incluent la mise en œuvre en C et la rédaction d'une documentation complète.

Sur ce, permettez-moi de prendre congé, merci de votre attention.Je serai infiniment heureux de tout commentaire.
J'espère que l'article et la bibliothèque vous seront utiles.
Signalez toute erreur (grammaticale et logique) - je la corrigerai.

PPS

Juste au cas où, voici un lien vers des interprètes en ligne (et pas seulement) Matlab / Octave, que j'utilise moi-même:

• Compilateur d'octave en ligne
• Octave en ligne
• GNU Octave