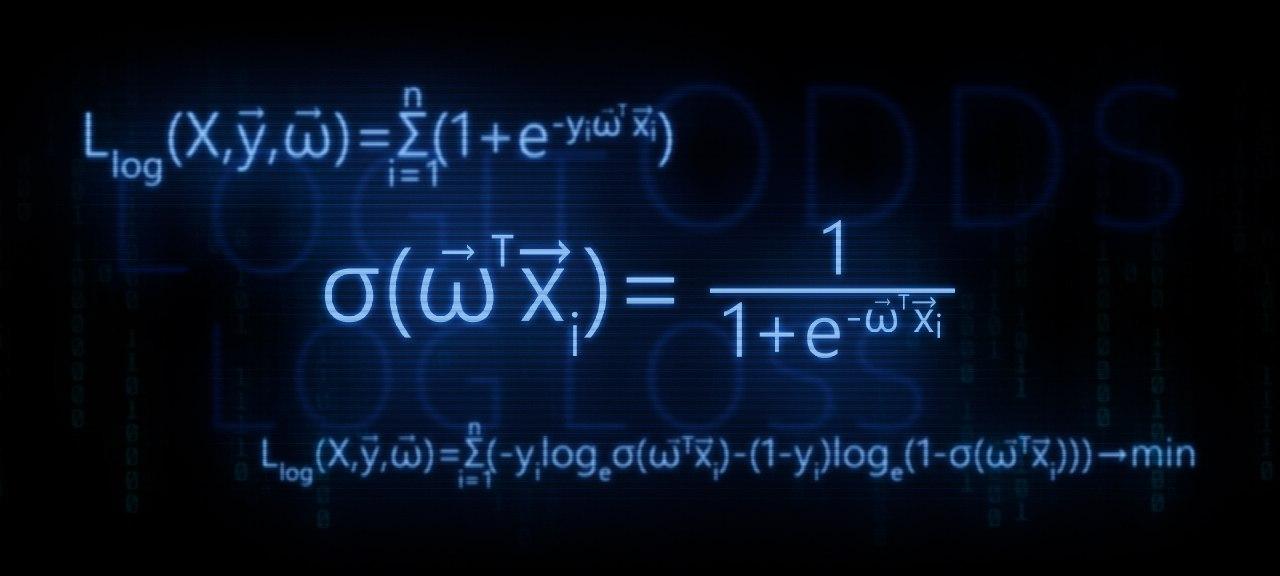
Dans cet article, nous analyserons les calculs théoriques de conversion de
la fonction de régression linéaire en fonction de transformation logarithmique inverse (en d'autres termes, la fonction de réponse logistique) . Ensuite, en utilisant l'arsenal de
la méthode du maximum de vraisemblance , conformément au modèle de régression logistique, nous dérivons la fonction
de perte Perte logistique , ou en d'autres termes, nous déterminons la fonction par laquelle les paramètres du vecteur de poids sont sélectionnés dans le modèle de régression logistique
vecw .
Le plan de l'article:
- Répétons la relation simple entre deux variables
- Nous identifions le besoin de convertir la fonction de régression linéaire f(w,xi)= vecwT vecxi à la fonction de réponse logistique sigma( vecwT vecxi)= frac11+e− vecwT vecxi
- Nous réalisons les transformations et dérivons la fonction de réponse logistique
- Essayons de comprendre pourquoi la méthode des moindres carrés est mauvaise lors du choix des paramètres vecw Caractéristiques de perte logistique
- Nous utilisons la méthode du maximum de vraisemblance pour déterminer la fonction de sélection des paramètres vecw :
5.1. Cas 1: fonction de perte logistique pour les objets avec la désignation de classe 0 et 1 :
Llog(X, vecy, vecw)= sum limitsni=1(−yi mkern2muloge mkern5mu sigma( vecwT vecxi)−(1−yi) mkern2muloge mkern5mu(1− sigma( vecwT vecxi))) rightarrowmin
5.2. Cas 2: Fonction de perte logistique pour les objets avec les désignations de classe -1 et +1 :
Llog(X, vecy, vecw)= sum limitsni=1 mkern2muloge mkern5mu(1+e−yi vecwT vecxi) rightarrowmin
L'article est rempli d'exemples simples dans lesquels tous les calculs sont faciles à faire verbalement ou sur papier, dans certains cas, une calculatrice peut être nécessaire. Alors préparez-vous :)
Cet article est plus destiné aux spécialistes des données ayant un niveau initial de connaissances dans les bases de l'apprentissage automatique.
L'article fournira également du code pour dessiner des graphiques et des calculs. Tout le code est écrit en
python 2.7 . Je vais expliquer à l'avance la «nouveauté» de la version utilisée - c'est l'une des conditions pour suivre un cours bien connu de
Yandex sur la plate-forme en ligne non moins bien connue pour l'enseignement en ligne
Coursera , et, comme vous pouvez le supposer, le matériel a été préparé sur la base de ce cours.
01. Ligne droite
Il est tout à fait raisonnable de se poser la question - où est la relation directe et la régression logistique?
Tout est simple! La régression logistique est l'un des modèles qui appartiennent au classificateur linéaire. En termes simples, l'objectif d'un classificateur linéaire est de prédire les valeurs cibles
y à partir de variables (régresseurs)
X . On pense que la relation entre les signes
X et valeurs cibles
y linéaire. Par conséquent, le nom du classificateur lui-même est linéaire. Généralisé très grossièrement, le modèle de régression logistique est basé sur l'hypothèse qu'il existe une relation linéaire entre les caractéristiques
X et valeurs cibles
y . Le voici - une connexion.
Le studio est le premier exemple, à juste titre, de la dépendance directe des quantités étudiées. Dans le processus de préparation de l'article, je suis tombé sur un exemple qui a déjà
eu mal à la gorge - la dépendance de l'intensité du courant sur la tension
(«Analyse de régression appliquée», N. Draper, G. Smith) . Ici, nous le considérerons aussi.
Conformément à la
loi d'
Ohm:I=U/R où
I - force actuelle
U - tension
R - résistance.
Si nous ne connaissions pas la
loi d'Ohm , nous pourrions trouver la dépendance empiriquement en changeant
U et mesurer
I tout en soutenant
R fixe. Ensuite, nous verrions que le graphique de dépendance
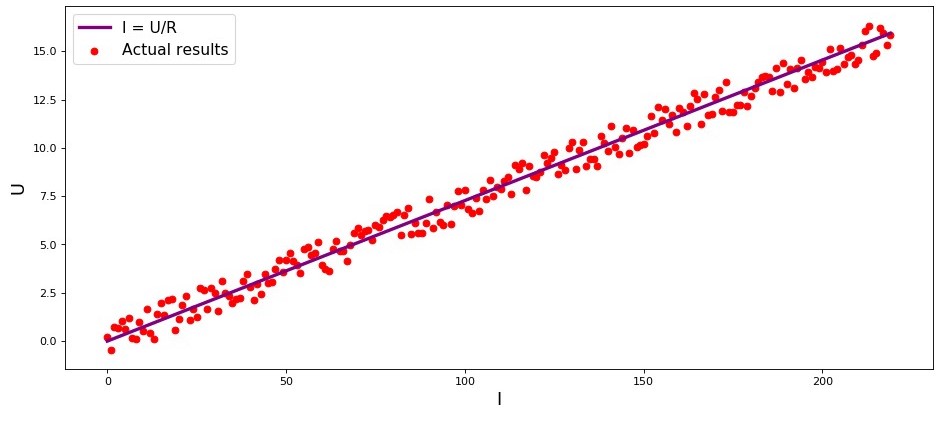
I de
U donne une ligne plus ou moins droite passant par l'origine. Nous avons dit «plus ou moins», car, bien que la dépendance soit en fait exacte, nos mesures peuvent contenir de petites erreurs, et donc les points sur le graphique peuvent ne pas tomber exactement sur la ligne, mais seront dispersés au hasard autour d'elle.
Graphique 1 «Dépendance
I de
U "
Code de rendu graphiqueimport matplotlib.pyplot as plt %matplotlib inline import numpy as np import random R = 13.75 x_line = np.arange(0,220,1) y_line = [] for i in x_line: y_line.append(i/R) y_dot = [] for i in y_line: y_dot.append(i+random.uniform(-0.9,0.9)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(x_line,y_line,color = 'purple',lw = 3, label = 'I = U/R') plt.scatter(x_line,y_dot,color = 'red', label = 'Actual results') plt.xlabel('I', size = 16) plt.ylabel('U', size = 16) plt.legend(prop = {'size': 14}) plt.show()
02. Le besoin de transformations de l'équation de régression linéaire
Prenons un autre exemple. Imaginez que nous travaillons dans une banque et que nous soyons confrontés à la tâche de déterminer la probabilité de remboursement d'un prêt par un emprunteur, en fonction de certains facteurs. Pour simplifier la tâche, nous considérons seulement deux facteurs: le salaire mensuel de l'emprunteur et le paiement mensuel pour le remboursement du prêt.
La tâche est très conditionnelle, mais avec cet exemple, nous pouvons comprendre pourquoi il ne suffit pas d'utiliser
la fonction de régression linéaire pour la résoudre, et nous découvrirons également quelles transformations avec la fonction que vous devez effectuer.
Nous revenons par exemple. Il est entendu que plus le salaire est élevé, plus l'emprunteur pourra diriger mensuellement pour rembourser le prêt. Dans le même temps, pour une certaine fourchette de salaires, cette dépendance sera assez linéaire pour elle-même. Par exemple, prenez une fourchette de salaire de 60 000 à 200 000 et supposez que dans la fourchette de salaires indiquée, la dépendance de la taille du paiement mensuel sur le montant du salaire est linéaire. Supposons que, pour la fourchette de salaires spécifiée, il ait été révélé que le rapport du salaire au paiement ne peut pas tomber en dessous de 3 et que l'emprunteur devrait encore avoir 5.000 en réserve. Et seulement dans ce cas, nous supposerons que l'emprunteur remboursera le prêt à la banque. Ensuite, l'équation de régression linéaire prend la forme:
f(w,xi)=w0+w1xi1+w2xi2,où
w0=−5,000 ,
w1=1 ,
w2=−3 ,
xi1 -
salaire i emprunteur
xi2 -
paiement du prêt i emprunteur.
Substitution du salaire et du paiement du prêt par des paramètres fixes dans l'équation
vecw Vous pouvez décider d'accorder ou de refuser un prêt.
Pour l'avenir, nous notons que, pour des paramètres donnés
vecw la fonction de régression linéaire utilisée dans
la fonction de réponse logistique produira des valeurs importantes qui rendent difficile le calcul des probabilités de remboursement du prêt. Par conséquent, il est proposé de réduire nos coefficients, disons, 25 000 fois. A partir de cette conversion en ratios, la décision d'octroyer un prêt ne changera pas. Souvenons-nous de ce moment pour l'avenir, et maintenant, pour que ce soit encore plus clair, nous allons examiner la situation avec trois emprunteurs potentiels.
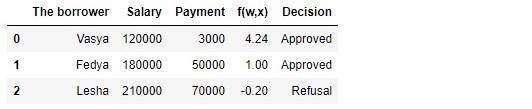
Tableau 1 "Emprunteurs potentiels"
Code de génération de la table import pandas as pd r = 25000.0 w_0 = -5000.0/r w_1 = 1.0/r w_2 = -3.0/r data = {'The borrower':np.array(['Vasya', 'Fedya', 'Lesha']), 'Salary':np.array([120000,180000,210000]), 'Payment':np.array([3000,50000,70000])} df = pd.DataFrame(data) df['f(w,x)'] = w_0 + df['Salary']*w_1 + df['Payment']*w_2 decision = [] for i in df['f(w,x)']: if i > 0: dec = 'Approved' decision.append(dec) else: dec = 'Refusal' decision.append(dec) df['Decision'] = decision df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision']]
Selon le tableau, Vasya, avec un salaire de 120.000, veut obtenir un tel prêt afin de le rembourser à 3.000 mensuellement. Nous avons déterminé que pour approuver le prêt, le salaire de Vasya devait être trois fois le montant du paiement, et qu'il resterait alors 5.000P. Vasya satisfait à cette exigence:

. Il reste même 106 000P. Malgré le fait que lors du calcul
f(w,xi) nous avons réduit les chances
vecw 25 000 fois, le résultat est le même: le prêt peut être approuvé. Fedya recevra également un prêt, mais Lesha, malgré le fait qu'il en reçoive le plus, devra restreindre son appétit.
Dessinons un calendrier pour ce cas.
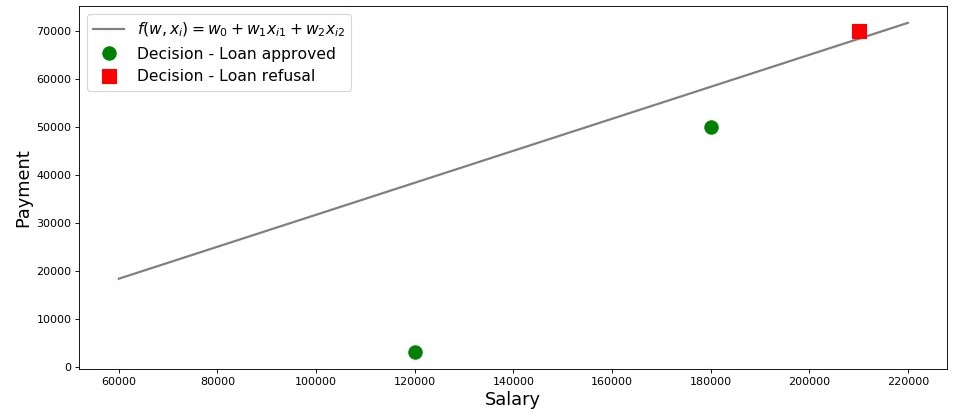
Graphique 2 «Classification des emprunteurs»
Code de traçage salary = np.arange(60000,240000,20000) payment = (-w_0-w_1*salary)/w_2 fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(salary, payment, color = 'grey', lw = 2, label = '$f(w,x_i)=w_0 + w_1x_{i1} + w_2x_{i2}$') plt.plot(df[df['Decision'] == 'Approved']['Salary'], df[df['Decision'] == 'Approved']['Payment'], 'o', color ='green', markersize = 12, label = 'Decision - Loan approved') plt.plot(df[df['Decision'] == 'Refusal']['Salary'], df[df['Decision'] == 'Refusal']['Payment'], 's', color = 'red', markersize = 12, label = 'Decision - Loan refusal') plt.xlabel('Salary', size = 16) plt.ylabel('Payment', size = 16) plt.legend(prop = {'size': 14}) plt.show()
Ainsi, notre ligne, construite conformément à la fonction
f(w,xi)=w0+w1xi1+w2xi2 , sépare les «mauvais» emprunteurs des «bons». Les emprunteurs dont les désirs ne coïncident pas avec les opportunités sont au dessus de la ligne directe (Lesha), ceux qui sont en mesure de rembourser le prêt selon les paramètres de notre modèle sont sous la ligne directe (Vasya et Fedya). Sinon, nous pouvons dire ceci - notre ligne divise les emprunteurs en deux classes. Nous les désignons comme suit: à la classe
+1 classer les emprunteurs susceptibles de rembourser le prêt à la classe
−1 ou
0 nous assignerons les emprunteurs qui ne seront probablement pas en mesure de rembourser le prêt.
Résumez les conclusions de cet exemple simple. Prenez un point
M(x1,x2) et, en remplaçant les coordonnées du point dans l'équation correspondante de la ligne
f(w,xi)=w0+w1xi1+w2xi2 , envisagez trois options:
- Si le point est sous la ligne, et nous l'assignons à la classe +1 , puis la valeur de la fonction f(w,xi)=w0+w1xi1+w2xi2 sera positif de 0 avant + infty . Nous pouvons donc supposer que la probabilité de remboursement du prêt est inférieure à (0,5,1] . Plus la valeur de la fonction est élevée, plus la probabilité est élevée.
- Si le point est au-dessus de la ligne et que nous le rapportons à la classe −1 ou 0 , alors la valeur de la fonction sera négative de 0 avant − infty . Ensuite, nous supposerons que la probabilité de remboursement de la dette est inférieure à [0,0,5) et, plus la valeur de la fonction modulo est élevée, plus notre confiance est élevée.
- Le point est sur une ligne droite, à la frontière entre deux classes. Dans ce cas, la valeur de la fonction f(w,xi)=w0+w1xi1+w2xi2 sera égal 0 et la probabilité de remboursement du prêt est égale à
 .
.
Maintenant, imaginez que nous n'avons pas deux facteurs, mais des dizaines, des emprunteurs non pas trois, mais des milliers. Ensuite, au lieu d'une ligne droite, nous aurons un plan à
m dimensions et des coefficients
w nous ne serons pas prélevés sur le plafond, mais retirés conformément à toutes les règles, mais sur la base des données accumulées sur les emprunteurs qui ont remboursé ou non le prêt. Et vraiment, attention, nous sélectionnons maintenant des emprunteurs avec des ratios déjà connus
w . En fait, la tâche du modèle de régression logistique est précisément de déterminer les paramètres
w à laquelle la valeur de la fonction
de perte Perte logistique tendra au minimum. Mais comment le vecteur est calculé
vecw , nous découvrons toujours dans la 5ème section de l'article. En attendant, nous retournons à la terre promise - à notre banquier et à ses trois clients.
Merci à la fonction
f(w,xi)=w0+w1xi1+w2xi2 nous savons qui peut bénéficier d'un prêt et qui doit être refusé. Mais vous ne pouvez pas vous adresser au directeur avec de telles informations, car il voulait obtenir de nous la probabilité de remboursement du prêt de chaque emprunteur. Que faire La réponse est simple - nous devons en quelque sorte transformer la fonction
f(w,xi)=w0+w1xi1+w2xi2 dont les valeurs se situent dans la plage
(− infty,+ infty) sur une fonction dont les valeurs se situent dans la plage
[0,1] . Et une telle fonction existe, elle s'appelle la
fonction de réponse logistique ou conversion en logit inverse . Rencontrez:
sigma( vecwT vecxi)= frac11+e− vecwT vecxi
Voyons les étapes pour obtenir
la fonction de réponse logistique . Notez que nous allons avancer dans la direction opposée, c'est-à-dire nous supposons que nous connaissons la valeur de la probabilité, qui se situe dans la plage de
0 avant
1 puis nous allons "tourner" cette valeur sur toute la plage de nombres de
− infty avant
+ infty .
03. Sortie de la fonction de réponse logistique
Étape 1. Transférez les valeurs de probabilité dans la plage [0,+ infty)
Au moment de la transformation des fonctions
f(w,xi)=w0+w1xi1+w2xi2 à
la fonction de réponse logistique sigma( vecwT vecxi)= frac11+e vecwT vecxi nous laisserons notre analyste de crédit tranquille, et passerons plutôt par les bookmakers. Non, bien sûr, nous ne ferons pas de paris, tout ce qui nous intéresse, c'est le sens de l'expression, par exemple, une chance de 4 pour 1. Les cotes familières à tous les joueurs de paris sont le rapport des «succès» aux «échecs». En termes de probabilités, les chances sont la probabilité qu'un événement se produise divisé par la probabilité que l'événement ne se produise pas. Nous écrivons la formule pour la chance d'un événement
(cote+) :
odds+= fracp+1−p+
où
p+ - probabilité d'occurrence d'un événement,
(1−p+) - probabilité de NON apparition d'un événement
Par exemple, si la probabilité qu'un cheval jeune, fort et fougueux, surnommé "Veterok" batte lors des courses, une vieille femme flasque surnommée "Matilda" est égale à

, alors les chances de succès de Veterka seront
4 à
1(0,8/(1−0,8)) et vice versa, connaissant les chances, il ne nous sera pas difficile de calculer la probabilité
p+ :
fracp+1−p+=4 mkern15mu Longrightarrow mkern15mup+=4(1−p+) mkern15mu Longrightarrow mkern15mu5p+=4 mkern15mu Longrightarrow mkern15mup+=0,8Ainsi, nous avons appris à «traduire» la probabilité en cotes qui prennent des valeurs de
0 avant
+ infty . Faisons un pas de plus et apprenons à «traduire» la probabilité sur la droite entière de
− infty avant
+ infty .
Étape 2. Nous traduisons les valeurs de probabilité dans la plage (− infty,+ infty)
Cette étape est très simple - nous prologue les cotes en fonction du nombre d'Euler
e et obtenez:
f(w,xi)= vecwT vecx=ln(cote+)
Maintenant, nous savons que si
p+=0,8 puis calculez la valeur
f(w,xi) ce sera très simple et, en plus, ça devrait être positif:
f(w,xi)=ln(cote+)=ln(0,8/0,2)=ln(4) environ+1,38629 . Il en est ainsi.
Par curiosité, nous vérifions que si
p+=0,2 nous nous attendons à voir une valeur négative
f(w,xi) . Nous vérifions:
f(w,xi)=ln(0,2/0,8)=ln(0,25) environ−1,38629 . D'accord.
Maintenant, nous savons comment traduire la valeur de probabilité de
0 avant
1 sur toute la ligne numérique de
− infty avant
+ infty . À l'étape suivante, nous ferons le contraire.
En attendant, on note que conformément aux règles du logarithme, connaître la valeur de la fonction
f(w,xi) , vous pouvez calculer les cotes:
odds+=ef(w,xi)=e vecwT vecx
Cette méthode de détermination des chances vous sera utile à l'étape suivante.
Étape 3. Nous dérivons une formule pour déterminer p+
Nous avons donc appris, sachant
p+ trouver des valeurs de fonction
f(w,xi) . Cependant, en fait, nous avons besoin de tout exactement le contraire - connaître la valeur
f(w,xi) trouver
p+ . Pour ce faire, nous nous tournons vers un concept tel que la fonction inverse des chances, selon lequel:
p+= fracodds+1+odds+
Dans l'article, nous ne dériverons pas la formule ci-dessus, mais vérifions les chiffres de l'exemple ci-dessus. Nous savons qu'avec des cotes de 4 à 1 (
cotes+=4 ), la probabilité qu'un événement se produise est de 0,8 (
p+=0,8 ) Faisons une substitution:
p+= frac41+4=0,8 . Cela coïncide avec nos calculs effectués précédemment. Nous continuons.
Dans la dernière étape, nous avons déduit que
odds+=e vecwT vecx , ce qui signifie que vous pouvez effectuer une substitution dans la fonction inverse des cotes. Nous obtenons:
p+= frace vecwT vecx1+e vecwT vecx
Divisez le numérateur et le dénominateur par
e vecwT vecx puis:
p+= frac11+e− vecwT vecx= sigma( vecwT vecx)
Pour chaque pompier, afin de nous assurer que nous n’avons commis aucune erreur, nous ferons encore une petite vérification. À l'étape 2, nous sommes pour
p+=0,8 déterminé que
f(w,xi) environ+1,38629 . Ensuite, en remplaçant la valeur
f(w,xi) dans la fonction de réponse logistique, nous nous attendons à obtenir
p+=0,8 . Remplacez et obtenez:
p+= frac11+e−1.38629=0,8Félicitations, cher lecteur, nous venons de développer et de tester la fonction de réponse logistique. Regardons le graphe de fonction.
Graphique 3 «Fonction de réponse logistique»

Code de traçage import math def logit (f): return 1/(1+math.exp(-f)) f = np.arange(-7,7,0.05) p = [] for i in f: p.append(logit(i)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(f, p, color = 'grey', label = '$ 1 / (1+e^{-w^Tx_i})$') plt.xlabel('$f(w,x_i) = w^Tx_i$', size = 16) plt.ylabel('$p_{i+}$', size = 16) plt.legend(prop = {'size': 14}) plt.show()
Dans la littérature, vous pouvez également trouver le nom de cette fonction en tant que
fonction sigmoïde . Le graphique montre clairement que le principal changement dans la probabilité d'appartenance d'un objet à une classe se produit dans une plage relativement petite
f(w,xi) quelque part
−4 avant
+4 .
Je propose de revenir à notre analyste crédit et de l'aider à calculer la probabilité de remboursement des prêts, sinon il court le risque de se retrouver sans bonus :)
Tableau 2 "Emprunteurs potentiels"
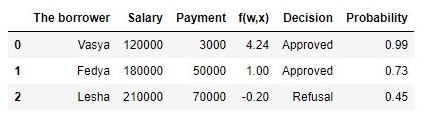
Code de génération de la table proba = [] for i in df['f(w,x)']: proba.append(round(logit(i),2)) df['Probability'] = proba df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision', 'Probability']]
Nous avons donc déterminé la probabilité de remboursement du prêt. Dans l'ensemble, cela semble être vrai.
En effet, la probabilité que Vasya avec un salaire de 120 000 puisse donner 3.000 mensuellement à la banque est proche de 100%. Soit dit en passant, nous devons comprendre que la banque peut également accorder un prêt à Lesha si la politique de la banque prévoit, par exemple, de prêter aux clients avec une probabilité de remboursement du prêt supérieure à, disons, 0,3. Dans ce cas, la banque constituera une réserve plus importante pour d'éventuelles pertes.
Il convient également de noter que le rapport du salaire au paiement d'au moins 3 et avec une marge de 5.000 a été prélevé sur le plafond. Par conséquent, nous n'avons pas pu utiliser le vecteur de poids dans sa forme d'origine
vecw=(−5000,1,−3) . Nous devions réduire considérablement les coefficients, et dans ce cas, nous avons divisé chaque coefficient par 25 000, c'est-à-dire que nous avons ajusté le résultat. Mais cela a été fait exprès pour simplifier la compréhension du matériel au stade initial. Dans la vie, il ne faut pas inventer et ajuster les coefficients, mais les trouver. Juste dans les prochaines sections de l'article, nous dériverons les équations avec lesquelles les paramètres sont sélectionnés
vecw .
04. Méthode des moindres carrés pour déterminer le vecteur de poids vecw dans la fonction de réponse logistique
Nous connaissons déjà une telle méthode pour sélectionner un vecteur de poids
vecw comme
la méthode des moindres carrés (OLS) et, en fait, pourquoi ne l'utilisons-nous pas alors dans les problèmes de classification binaire? En effet, rien n'empêche l'utilisation des
MNC , seule cette méthode dans les problèmes de classification donne des résultats moins précis que la
Perte Logistique . Il y a une justification théorique à cela. Commençons par regarder un exemple simple.
Supposons que nos modèles (utilisant
MSE et
Logistic Loss ) aient déjà commencé la sélection du vecteur de poids
vecw et nous avons arrêté le calcul à un moment donné. Peu importe, au milieu, à la fin ou au début, l'essentiel est que nous ayons déjà quelques valeurs du vecteur de poids et supposons, à cette étape, le vecteur de poids
vecw pour les deux modèles n'ont pas de différences. Ensuite, nous prenons les poids obtenus et les substituons dans
la fonction de réponse logistique (
frac11+e− vecwT vecx ) pour un objet appartenant à la classe
+1 . Nous étudierons deux cas où, conformément au vecteur de poids sélectionné, notre modèle se trompe grandement et vice versa - le modèle est fortement confiant que l'objet appartient à la classe
+1 . Voyons quelles amendes seront "émises" lors de l'utilisation de
MNC et
de perte logistique .
Code de calcul des amendes en fonction de la fonction de perte utilisée Le cas avec une erreur brute - le modèle classe l'objet
+1 avec une probabilité de 0,01
La pénalité lors de l'utilisation d'
OLS est:
MSE=(y−p+)=(1−0,01)2=0,9801La pénalité lors de l'utilisation
de Perte logistique est:
Pertedejournal=loge(1+e−yf(w,x))=loge(1+e−1(−4.595...)) environ4,605Cas avec une grande certitude - le modèle classe l'objet
+1 avec une probabilité de 0,99
La pénalité lors de l'utilisation d'
OLS est:
MSE=(1−0,99)2=0,0001La pénalité lors de l'utilisation
de Perte logistique est:
Pertedejournal=loge(1+e−4.595...) environ0,01Cet exemple illustre bien qu'avec une erreur brute, la fonction de perte de
perte de journal inflige une amende beaucoup plus importante au modèle que
MSE . Voyons maintenant quelles sont les conditions préalables théoriques pour utiliser la fonction de perte de
perte de journal dans les problèmes de classification.
05. Méthode de crédibilité maximale et régression logistique
Comme promis au début, l'article regorge d'exemples simples. Dans le studio, un autre exemple et d'anciens invités sont les emprunteurs de la banque: Vasya, Fedya et Lesha.
Pour chaque pompier, avant de développer un exemple, permettez-moi de vous rappeler que dans la vie, nous avons affaire à un échantillon d'entraînement de milliers ou de millions d'objets avec des dizaines ou des centaines de signes. Cependant, ici, les chiffres sont pris de sorte qu'ils s'intègrent facilement dans la tête d'un dataintest novice.
Nous revenons par exemple. Imaginez que le directeur de la banque ait décidé d'accorder un prêt à tous ceux qui en avaient besoin, malgré le fait que l'algorithme ait suggéré de ne pas le donner à Lesha. Et donc assez de temps s'est écoulé et nous avons réalisé lequel des trois héros a remboursé le prêt et qui ne l'a pas fait. À quoi s'attendre: Vasya et Fedya ont remboursé le prêt, mais Alex ne l'a pas fait. Imaginons maintenant que ce résultat soit un nouvel échantillon de formation pour nous et, en même temps, toutes les données sur les facteurs affectant la probabilité de remboursement du prêt (salaire de l'emprunteur, montant du paiement mensuel) semblent avoir disparu. Ensuite, intuitivement, nous pouvons supposer qu'un emprunteur sur trois ne rembourse pas un prêt à la banque, ou en d'autres termes, la probabilité qu'un prêt soit remboursé par l'emprunteur suivant
p= frac23 . Il existe des preuves théoriques de cette hypothèse intuitive et elle est basée sur la
méthode du
maximum de vraisemblance , souvent appelée dans la littérature
le principe du maximum de vraisemblance .
Tout d'abord, familiarisez-vous avec l'appareil conceptuel.
La probabilité d'un
échantillon est la probabilité d'obtenir exactement un tel échantillon, d'obtenir précisément ces observations / résultats, c'est-à-dire le produit des probabilités d'obtenir chacun des résultats de l'échantillon (par exemple, le prêt de Vasya, Feday et Lesha en même temps a été remboursé ou non remboursé).
La fonction de vraisemblance associe la vraisemblance d'un échantillon aux valeurs des paramètres de distribution.
Dans notre cas, l'échantillon d'apprentissage est un schéma de Bernoulli généralisé dans lequel une variable aléatoire ne prend que deux valeurs:
1 ou
0 . Par conséquent, la probabilité de l'échantillon peut être écrite en fonction de la probabilité du paramètre
p comme suit:
P( mkern5mu vecy mkern5mu| mkern5mup)= prod limits3i=1pyi(1−p)(1−yi) mkern5mu= mkern5mup1(1−p)1−1 centerdotp1(1−p)1−1 centerdotp0(1−p)1−0 mkern5mu== mkern5mup centerdotp centerdot(1−p) mkern5mu= mkern5mup2(1−p)L'enregistrement ci-dessus peut être interprété comme suit. La probabilité conjointe que Vasya et Fedya remboursent le prêt est égale à
p centerdotp=p2 , la probabilité qu'Alex ne rembourse PAS le prêt est
1−p (puisqu'il ne s'agissait PAS du remboursement du prêt), la probabilité conjointe des trois événements est donc
p2(1−p) .
La méthode du
maximum de vraisemblance est une méthode d'estimation d'un paramètre inconnu en maximisant
la fonction de vraisemblance .
p ,
P(→y|p)=p2(1−p) .
– , ? , – , , . , , . , , , , – , . , , .
, , . , . , —
. ? ,
P(→y|p) , ,
p ,
P(→y|p) . ( ), — .
, , , .
:
logP(→y|p)=logp2(1−p)=2logp+log(1−p)p :
∂logP(→y|p)∂p=∂∂p(2logp+log(1−p))=2p−11−p, — :
2p−11−p=0⟹2p=11−p⟹2(1−p)=p⟹p=23,
p=23 .
, ? , , . - ,
23 , : . , . ,
23 .
:
from functools import reduce def likelihood(y,p): line_true_proba = [] for i in range(len(y)): ltp_i = p[i]**y[i]*(1-p[i])**(1-y[i]) line_true_proba.append(ltp_i) likelihood = [] return reduce(lambda a, b: a*b, line_true_proba) y = [1.0,1.0,0.0] p_log_response = df['Probability'] const = 2.0/3.0 p_const = [const, const, const] print ' p=2/3:', round(likelihood(y,p_const),3) print '****************************************************************************************************' print ' p:', round(likelihood(y,p_log_response),3)
, . ? , . , , , 3- , .
,
, - , , , , 0.99, 0.99 0.01 . ,
1 , , -, , , -, . , ( ) , . , . ? , . 2.5% , — 27,8%. 2 « » , , , . , ,
f(w,x)=w0+w1x1+w2x2 : 4.24 1.0 . , , , . , .
w , , ,
w , ,
w , — :)
.
→w , .
,
w :
1. , ( ) , — .
f(w,x)=→wTX , ()
+1 et
−1 ou
0 (, ).
f(w,x)=w0+w1x1+w2x2 .
2.
- p+=11+e−→wT→x=σ(→wT→x) +1 .
3.
, ,
p ( ) 1
(1–p) – 0.
4. ,
, . , , . —
p ,
w .
→w , .
5. ,
. .
:)
,
Logistic Loss . , ,
+1 et
0 ou
−1 . , .
1. +1 et 0
, ,
w , :
P(→y|p)=3∏i=1pyi(1−p)(1−yi)En fait
pi —
p+=11+e−→wT→x=σ(→wT→x) →w:
P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)yi(1−σ(→wT→xi)(1−yi)→max
, , , . 4 , :
1. yi=+1 (.. +1),
σ(→wTX)) +1 0.9, :
0.91⋅(1−0.9)(1−1)=0.91⋅0.10=0.92. yi=+1 ,
σ(→wTX))=0.1 , :
0.11⋅(1−0.1)(1−1)=0.11⋅0.90=0.13. yi=0 ,
σ(→wTX))=0.1 , :
0.10⋅(1−0.1)(1−0)=0.10⋅0.91=0.94. yi=0 ,
σ(→wTX))=0.9 , :
0.90⋅(1−0.9)(1−0)=0.90⋅0.11=0.1, 1 3 —
+1 .
,
+1 w , . , ,
w . :
.
Llog(X,→y,→w)=n∑i=1(−yilogeσ(→wT→xi)−(1−yi)loge(1−σ(→wT→xi)))→min
,
,
+ − . , ,
− , .
, , —
Logistic Loss :
+1 et
0 .
, ,
, , ,
w . , , , , , .
2. +1 et −1
,
1 et
0 ,
Logistic Loss , . .
«..., ...» . ,
i -
+1 ,
p ,
−1 ,
(1−p) . :
P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)[yi=+1](1−σ(→wT→xi)[yi=−1])→max
. 4 :
1. yi=+1 et
σ(→wT→xi)=0.9 , «»
0.92. yi=+1 et
σ(→wT→xi)=0.1 , «»
0.13. yi=−1 et
σ(→wT→xi)=0.1 , «»
1−0.1=0.94. yi=−1 et
σ(→wT→xi)=0.9 , «»
1−0.9=0.1, 1 3 , ,
, . , . , , .
Llog(X,→y,→w)=n∑i=1(−[yi=+1]logeσ(→wT→xi)−[yi=−1]loge(1−σ(→wT→xi)))→min
σ(→wT→xi) 11+e−→wT→xi :
Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(1−11+e−→wT→xi))→min
, :
Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(11+e→wT→xi))→min
«..., ...» . ,
yi +1 , , ,
e −→wT→xi ,
−1 , $e$
+→wT→xi . — :
−yi→wT→xi .
:
Llog(X,→y,→w)=n∑i=1−loge(11+e−yi→wT→xi)→min
, "
− " () , :
Llog(X,→y,→w)=n∑i=1loge(1+e−yi→wT→xi)→min
logistic Loss , :
+1 et
−1 .
, .
← — « »1.
1) / . , . – 2- . – .: , 1986 ( )
2) / .. — 9- . — .: , 2003
3) / .. — : , 2007
4) -: / . ., . . — 2- . — -: , 2013
5) Data Science / — -: , 2017
6) Data Science / ., . — -: , 2018
2. , ()
1)
,2)
,3)
. ODS, Yury Kashnitsky4)
4, ( 47 )5)
,3. -
1)
2)
3)
4)
5)
6)
7)
8)
e ?9)