कुछ त्वरण सेंसर को बोर्ड पर बढ़ते हुए अतिरिक्त शून्य अंशांकन की आवश्यकता होती है। जब मैंने त्वरण सेंसरों के अंशांकन के साथ कई स्रोतों को देखा, जहां Z घटक को केवल Z अक्ष से 9.8 m / s2 घटाकर ध्यान में रखा गया था, तो इस नोट को लिखने के लिए विचार आया।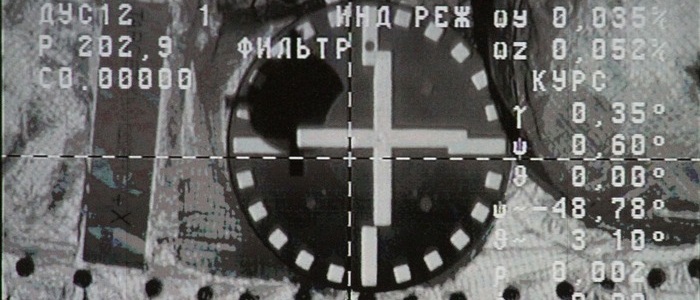
प्रकाशन संरचना
- मुसीबत
- समस्या और समाधान की विधि का कथन
- अंक कैसे प्राप्त करें?
- गेंद के केंद्र की गणना कैसे करें?
- गेंद के केंद्र की खोज कैसे तेज करें?
- गेंद के केंद्र की खोज को गति देने के लिए और कैसे?
- माप त्रुटियों के बारे में
- संपूर्ण
मुसीबत
समस्या क्या है - बोर्ड में स्थापना के बाद एमईएमएस सेंसर मामूली विकृति से गुजरते हैं जो प्रभावित करते हैं:- शून्य स्थिति;
- मापा मूल्यों की स्केलिंग;
- एक दूसरे के लिए कुल्हाड़ियों की लंबवतता।
और अगर स्केलिंग और लंबवतता का उल्लंघन किया जाता है, तो यह ध्यान देने योग्य नहीं है, तो शून्य की स्थिति स्पर्शरेखा में उलझ जाती है। उदाहरण के लिए, यदि आप MPU9250 सेंसर के एक्सेलेरोमीटर के शून्य मान का विशिष्ट मान m / s 2 में अनुवाद करते हैं , तो यह 0.2 m / s 2 के क्षेत्र में प्राप्त होता है । यही है, सेंसर स्थिर है, लेकिन यह त्वरण दिखाता है, और 5 सेकंड के बाद हमें 1 m / s की गति मिलती है। एक तरफ, सभी सेंसर डेटा को हमेशा किसी प्रकार के फिल्टर (उदाहरण के लिए, जैसे ) के माध्यम से पारित किया जाता है । लेकिन दूसरी तरफ, इस पूर्वाग्रह के लिए फ़िल्टर को लगातार क्षतिपूर्ति क्यों करनी चाहिए? आखिरकार, सेंसर आंदोलन दिखाएगा जहां यह नहीं है। इससे परिणाम की सटीकता कम हो जाती है। सब सब में, आपको एक बार ऑफसेट मान को खोजने की आवश्यकता है और फिर सेंसर ऑपरेशन के दौरान इस मूल्य को इसके रीडिंग से घटाएं।शून्य ऑफसेट के मूल्य को खोजने का सबसे सरल समाधान, जो तुरंत दिमाग में आता है, उन परिस्थितियों को बनाना है जिनके तहत सेंसर को शून्य को सटीक रूप से दिखाना होगा। सेंसर पर दर्ज मूल्य शून्य ऑफसेट का मूल्य है! इसलिए? लेकिन नहीं - गुरुत्वाकर्षण लगातार एक्सेलेरोमीटर पर काम कर रहा है। इससे बचने के लिए भारहीनता की आवश्यकता होगी (टॉस करने से काम नहीं चलेगा)। पृथ्वी का चुंबकीय क्षेत्र कम्पास, और गायरोस्कोप पर इसके रोटेशन पर कार्य करता है। इसलिए यदि आपके पास व्यक्तिगत स्टारशिप नहीं है, तो आपको कुछ लेना होगा।दूसरा समाधान जो तुरंत दिमाग में आता है, वह सेंसर (या इसके अक्ष) को उस स्थिति में रखना है, जिसमें हम यह जान पाएंगे कि सेंसर वास्तव में क्या दिखाता है। सेंसर क्या दिखाता है और उसे क्या दिखाना चाहिए - के बीच का अंतर और एक शून्य ऑफसेट होगा! इसलिए? उदाहरण के लिए, हम जानते हैं कि यदि एक्सीलरोमीटर को क्षितिज के साथ एक स्तर पर रखा जाता है, तो सिद्धांत रूप में, गुरुत्वाकर्षण त्वरण वेक्टर को सेंसर के जेड अक्ष के साथ बिल्कुल निर्देशित किया जाएगा। त्वरण वेक्टर की भयावहता हम जानते हैं।हालांकि, वहाँ एक समस्या है। यह इस तथ्य में शामिल है कि हम सेंसर के अक्ष को क्षितिज के साथ एक स्तर तक ठीक से सेट नहीं कर सकते हैं। तथ्य यह है कि जिस सतह पर हम भरोसा करेंगे, वह मुद्रित सर्किट बोर्ड के समानांतर नहीं है। यह, बदले में, उस साइट के समानांतर नहीं है जिस पर सेंसर स्थित है। सेंसर खुद अपनी साइट पर बिल्कुल नहीं खड़ा होता है और सेंसर के अंदर की कुल्हाड़ियां सेंसर बॉडी के समानांतर नहीं होती हैं। 1 डिग्री से क्षितिज के सापेक्ष अक्ष को स्थापित करने में त्रुटि आकार में एक प्रक्षेपण को शून्य ऑफसेट के मूल्य के बराबर देती है, जिसे हम खोजना चाहते हैं। मैग्नेटोमीटर के मामले में, हम यह भी नहीं जानते हैं कि चुंबकीय क्षेत्र वेक्टर कहाँ निर्देशित है। सिद्धांत रूप में, उत्तर की ओर। लेकिन व्यवहार में, पृथ्वी का चुंबकीय क्षेत्र स्वयं तीव्रता और दिशा में विषम है। साथ ही, पास की धातु की वस्तुएं अपना समायोजन करती हैं।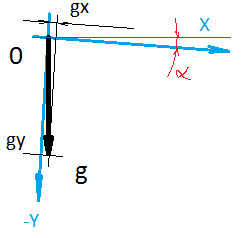
समस्या और समाधान की विधि का कथन
कार्य निम्नानुसार है: हमें सेंसर रीडिंग का उपयोग करके शून्य विस्थापन वेक्टर को निर्धारित करने की आवश्यकता है, जो हमेशा विस्थापन वेक्टर + निरंतर बाहरी प्रभाव वेक्टर (गुरुत्वाकर्षण त्वरण, पृथ्वी के घूर्णन, पृथ्वी के चुंबकीय क्षेत्र) को रिकॉर्ड करेगा, जिस परिमाण और दिशा का हमें पता नहीं है (एक्सेलेरोमीटर के मामले में) हम मूल्य जानते हैं, लेकिन फिर से सेंसर का पैमाना 1 के बराबर नहीं हो सकता है)।हल करने का तरीका। यह लेख विस्थापन वेक्टर को निम्नानुसार निर्धारित करने का प्रस्ताव करता है। हम सेंसर को हर तरह से लेते और मोड़ते हैं और सेंसर रीडिंग को रजिस्टर करते हैं। एन माप के बाद, सेंसर से लिया गया मान और ग्राफ पर स्थित एक गेंद होगी, जिसका त्रिज्या बाहरी प्रभाव का परिमाण है, और केंद्र सटीक वांछित शून्य ऑफसेट है।अंक कैसे प्राप्त करें?
माप प्रक्रिया को सुविधाजनक बनाने के लिए, आप एक सरल प्रोग्राम लिख सकते हैं। डिवाइस के स्थिर होने पर इसे सेंसर को रिकॉर्ड करना चाहिए। हमें केवल डिवाइस को वांछित स्थिति में बदलने की आवश्यकता है। एक स्थिर स्थिति निर्धारित करने के लिए, एक अनसाल्टेड एक्सेलेरोमीटर भी उपयुक्त है - बस वर्तमान मूल्य और पिछले एक के बीच का अंतर लें। और अगर अधिक शोर है, तो हम आंदोलन को ठीक करते हैं। मेरी सीमा 0.07G के क्षेत्र में प्राप्त की जाती है। यदि आप अपने हाथों से पकड़ते हैं, तो इससे अधिक मूल्य निकल जाएगा। मैंने स्थिति को ठीक करने के लिए मास्किंग टेप का उपयोग किया। यदि यह अभी भी काम नहीं करता है, तो यह देखने के लिए जांचें कि क्या कोई रेफ्रिजरेटर, एक प्रशंसक या कुछ समान है।यह कोड में कैसे हो सकता है
static TSumSensorsData g_sens_data[2];
static int32_t g_sens_data_sum_cnt[2];
static uint8_t g_sens_data_num;
IS_INTERRUPT void on_dma_raw_ready_calibrate_step1()
{
SensorRawBuffer *raw = sensor_get_raw_buffer();
g_sens_data[g_sens_data_num].acc_x += swap_i16(raw->accell_x_unswap);
g_sens_data[g_sens_data_num].acc_y += swap_i16(raw->accell_y_unswap);
g_sens_data[g_sens_data_num].acc_z += swap_i16(raw->accell_z_unswap);
g_sens_data[g_sens_data_num].gyro_x += swap_i16(raw->gyro_x_unswap);
g_sens_data[g_sens_data_num].gyro_y += swap_i16(raw->gyro_y_unswap);
g_sens_data[g_sens_data_num].gyro_z += swap_i16(raw->gyro_z_unswap);
g_sens_data[g_sens_data_num].mag_x += raw->mag_x_raw * g_mag_calibrate.kx;
g_sens_data[g_sens_data_num].mag_y += raw->mag_y_raw * g_mag_calibrate.ky;
g_sens_data[g_sens_data_num].mag_z += raw->mag_z_raw * g_mag_calibrate.kz;
g_sens_data_sum_cnt[g_sens_data_num]++;
}
void sensors_calibrate_program(FlashROM *flash_ptr)
{
double calibrate_result_error[3];
TVector16 calibrate_result[3];
int32_t radius[ACCEL_NO_MOTION_DETECT_COUNT];
uint8_t raw_is_deleted[ACCEL_NO_MOTION_DETECT_COUNT];
TVector16 raw[3][ACCEL_NO_MOTION_DETECT_COUNT];
. . .
g_sens_data_sum_cnt[0] = 0;
g_sens_data_num = 0;
int16_t prev_avg_x = 0;
int16_t prev_avg_y = 0;
int16_t prev_avg_z = 0;
int8_t low_motion_cnt = 0;
while(low_motion_cnt < ACCEL_NO_MOTION_DETECT_COUNT)
{
if (g_sens_data_sum_cnt[g_sens_data_num] >= ACCEL_NO_MOTION_DETECT_SAMPLES)
{
uint8_t new_data_num = (g_sens_data_num + 1) & 1;
g_sens_data[new_data_num].acc_x = 0;
g_sens_data[new_data_num].acc_y = 0;
g_sens_data[new_data_num].acc_z = 0;
g_sens_data[new_data_num].gyro_x = 0;
g_sens_data[new_data_num].gyro_y = 0;
g_sens_data[new_data_num].gyro_z = 0;
g_sens_data[new_data_num].mag_x = 0;
g_sens_data[new_data_num].mag_y = 0;
g_sens_data[new_data_num].mag_z = 0;
g_sens_data_sum_cnt[new_data_num] = 0;
uint8_t old_data_num = g_sens_data_num;
g_sens_data_num = new_data_num;
int16_t avg_x = g_sens_data[old_data_num].acc_x / g_sens_data_sum_cnt[old_data_num];
int16_t avg_y = g_sens_data[old_data_num].acc_y / g_sens_data_sum_cnt[old_data_num];
int16_t avg_z = g_sens_data[old_data_num].acc_z / g_sens_data_sum_cnt[old_data_num];
int16_t dx = avg_x - prev_avg_x;
int16_t dy = avg_y - prev_avg_y;
int16_t dz = avg_z - prev_avg_z;
prev_avg_x = avg_x;
prev_avg_y = avg_y;
prev_avg_z = avg_z;
if ((abs_i16(dx) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dy) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dz) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE))
{
raw[RAW_ACC][low_motion_cnt].x = avg_x;
raw[RAW_ACC][low_motion_cnt].y = avg_y;
raw[RAW_ACC][low_motion_cnt].z = avg_z;
raw[RAW_GYRO][low_motion_cnt].x = g_sens_data[old_data_num].gyro_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].y = g_sens_data[old_data_num].gyro_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].z = g_sens_data[old_data_num].gyro_z / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].x = g_sens_data[old_data_num].mag_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].y = g_sens_data[old_data_num].mag_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].z = g_sens_data[old_data_num].mag_z / g_sens_data_sum_cnt[old_data_num];
low_motion_cnt++;
beep();
delay_ms(2000);
}
}
}
. . .
}
गेंद को ग्राफ पर लाने के लिए, आपको एक निश्चित योजना के अनुसार सेंसर के साथ डिवाइस को मोड़ना होगा। इन उद्देश्यों के लिए, ग्लोब अच्छी तरह से अनुकूल है, क्योंकि इसमें एक मार्कअप है। आप सोच सकते हैं कि आपको दुनिया भर में मूर्तियां बनाने की आवश्यकता है। लेकिन यह ऐसा नहीं है।यह दुनिया की पूरी सतह पर नहीं, बल्कि एक मध्याह्न रेखा पर सेंसर को तराशने के लिए आवश्यक है। मान लीजिए कि हम मेरिडियन (उत्तर और दक्षिण ध्रुवों पर पहला और अंतिम) पर सात अंक लेते हैं। मध्याह्न के प्रत्येक बिंदु पर, हम आपके डिवाइस को ग्लोब से जोड़ते हैं और फिर भी एक निश्चित कदम के साथ अपनी धुरी पर डिवाइस को घुमाते हैं, उदाहरण के लिए 30-35 डिग्री। यह पता चला है कि यदि आप इसकी धुरी के चारों ओर 12 बार घूमते हैं, तो कुल 84 मापों में 7 अंक प्राप्त होते हैं। विधि की सुंदरता यह है कि सब कुछ "घुटने पर" किया जा सकता है। पोजिशनिंग सटीकता एक विशेष भूमिका नहीं निभाती है, आपको बस योजना के अनुसार मोड़ने की आवश्यकता है ताकि ग्राफ पर बाहरी प्रभाव का वेक्टर एक गेंद खींचे। सही एक ऐसा कुछ दिखता है - आंकड़ा देखें (केंद्र एक निशान के साथ चिह्नित है)।
विधि की सुंदरता यह है कि सब कुछ "घुटने पर" किया जा सकता है। पोजिशनिंग सटीकता एक विशेष भूमिका नहीं निभाती है, आपको बस योजना के अनुसार मोड़ने की आवश्यकता है ताकि ग्राफ पर बाहरी प्रभाव का वेक्टर एक गेंद खींचे। सही एक ऐसा कुछ दिखता है - आंकड़ा देखें (केंद्र एक निशान के साथ चिह्नित है)।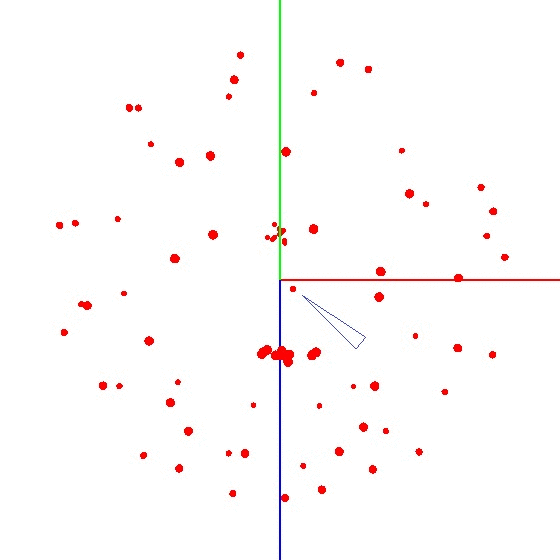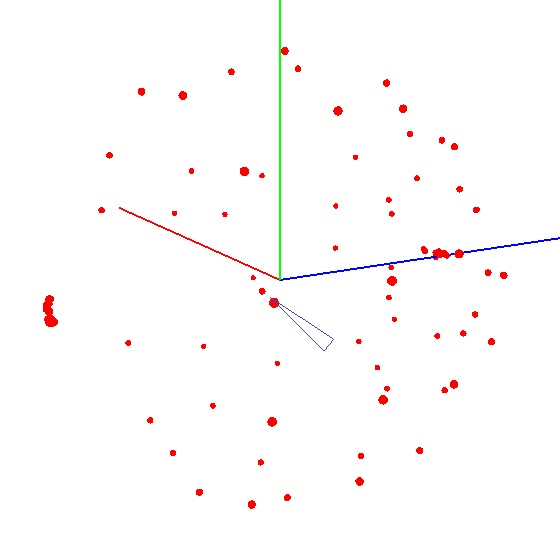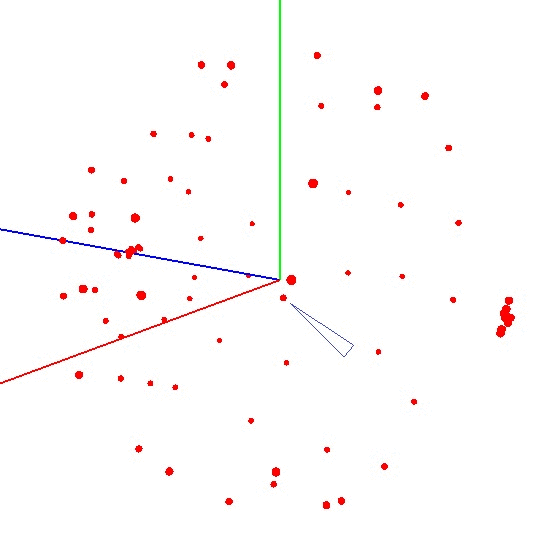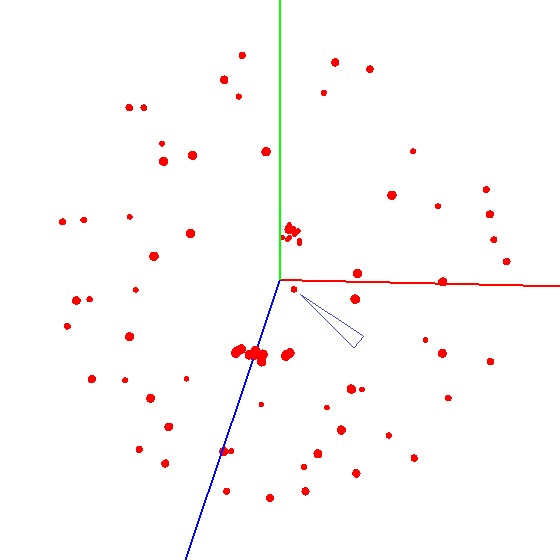
गेंद के केंद्र की गणना कैसे करें?
यह एक दिलचस्प काम है और इसके कई समाधान हैं। ऐसा लग सकता है कि केंद्र की खोज करने के लिए, प्राप्त बिंदुओं के निर्देशांक के अंकगणितीय औसत को लेना पर्याप्त है। हालांकि, यह ऐसा नहीं है - अंक गेंद पर असमान रूप से स्थित हो सकते हैं (देखें। अंजीर।)।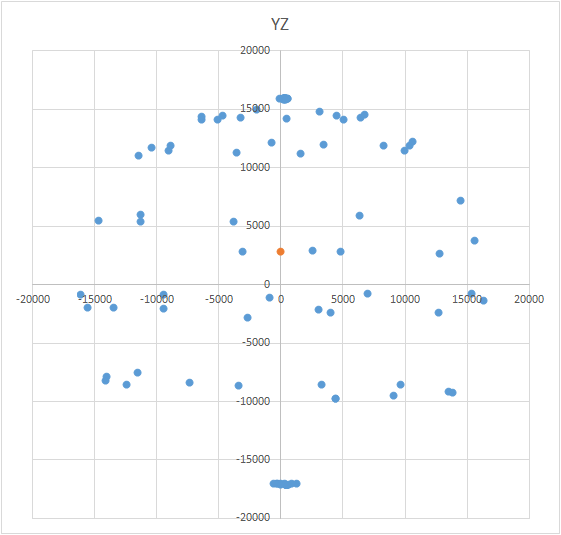 गेंद का समीकरण इस तरह दिखता है: (X - A) 2 + (Y - B) 2 + (Z - C) 2 = R 2 , जहाँ X, Y, Z गेंद पर पड़े बिंदु के निर्देशांक हैं। ए, बी, सी क्रमशः एक्स, वाई और जेड एक्सिस पर केंद्र के निर्देशांक हैं। R, गेंद की त्रिज्या है। आप समीकरणों की एक प्रणाली का निर्माण कर सकते हैं और इस प्रणाली को केवल कुछ विधि का उपयोग करके अधिक हल करने का प्रयास कर सकते हैं। या आप केवल केंद्र को खोजने के लिए बस्ट कर सकते हैं (यह क्रमिक अनुमानों की एक विधि की तरह है)। विधि का अर्थ सरल है: त्रुटि मान (एक्स - ए) 2 + (वाई - बी) 2+ (जेड - सी) 2 - आर 2 को शून्य करना चाहिए। इसका अर्थ है कि गोले के सभी बिंदुओं के लिए इन राशियों का योग भी शून्य होना चाहिए। यह जानते हुए, हम ए, बी और सी के लिए मान चुन सकते हैं, जिसके लिए सभी बिंदुओं के लिए त्रुटि न्यूनतम होगी। खोज क्षेत्र गेंद के आकार (सशर्त घन) द्वारा सीमित है। यही है, हमें अनुक्रमिक रूप से गेंद के केंद्र को क्यूब के सभी बिंदुओं पर रखना चाहिए और त्रुटि की गणना करनी चाहिए। जहां न्यूनतम त्रुटि है - केंद्र है।
गेंद का समीकरण इस तरह दिखता है: (X - A) 2 + (Y - B) 2 + (Z - C) 2 = R 2 , जहाँ X, Y, Z गेंद पर पड़े बिंदु के निर्देशांक हैं। ए, बी, सी क्रमशः एक्स, वाई और जेड एक्सिस पर केंद्र के निर्देशांक हैं। R, गेंद की त्रिज्या है। आप समीकरणों की एक प्रणाली का निर्माण कर सकते हैं और इस प्रणाली को केवल कुछ विधि का उपयोग करके अधिक हल करने का प्रयास कर सकते हैं। या आप केवल केंद्र को खोजने के लिए बस्ट कर सकते हैं (यह क्रमिक अनुमानों की एक विधि की तरह है)। विधि का अर्थ सरल है: त्रुटि मान (एक्स - ए) 2 + (वाई - बी) 2+ (जेड - सी) 2 - आर 2 को शून्य करना चाहिए। इसका अर्थ है कि गोले के सभी बिंदुओं के लिए इन राशियों का योग भी शून्य होना चाहिए। यह जानते हुए, हम ए, बी और सी के लिए मान चुन सकते हैं, जिसके लिए सभी बिंदुओं के लिए त्रुटि न्यूनतम होगी। खोज क्षेत्र गेंद के आकार (सशर्त घन) द्वारा सीमित है। यही है, हमें अनुक्रमिक रूप से गेंद के केंद्र को क्यूब के सभी बिंदुओं पर रखना चाहिए और त्रुटि की गणना करनी चाहिए। जहां न्यूनतम त्रुटि है - केंद्र है।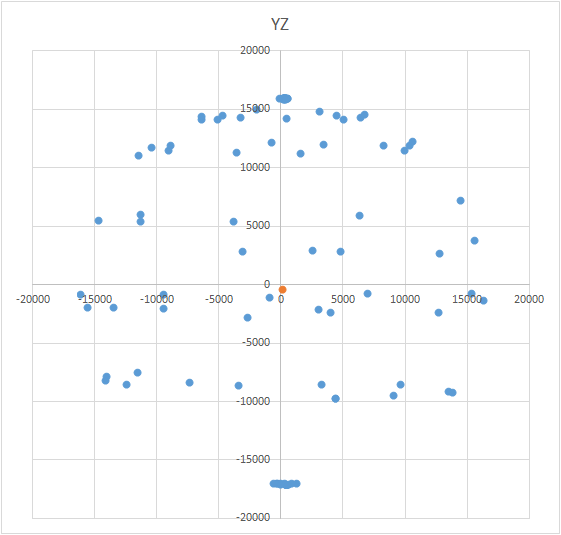 आर के रूप में, हमें बाह्य प्रभाव के वेक्टर के सैद्धांतिक मूल्य को लेने की जरूरत है - एक्सेलेरोमीटर के लिए, यह गुरुत्वाकर्षण का त्वरण है, कम्पास के लिए - यह पृथ्वी के चुंबकीय क्षेत्र का औसत परिमाण है, जाइरोस्कोप के लिए - पृथ्वी के रोटेशन की गति। बेशक, सूत्र में एक आयाम (सेंसर या एम / एस 2 की पारंपरिक इकाइयों) के मूल्य होने चाहिए, डिग्री / एस, आदि)। संबंधित सेंसर की मनमानी इकाइयों में परिवर्तित करना अधिक सुविधाजनक है।
आर के रूप में, हमें बाह्य प्रभाव के वेक्टर के सैद्धांतिक मूल्य को लेने की जरूरत है - एक्सेलेरोमीटर के लिए, यह गुरुत्वाकर्षण का त्वरण है, कम्पास के लिए - यह पृथ्वी के चुंबकीय क्षेत्र का औसत परिमाण है, जाइरोस्कोप के लिए - पृथ्वी के रोटेशन की गति। बेशक, सूत्र में एक आयाम (सेंसर या एम / एस 2 की पारंपरिक इकाइयों) के मूल्य होने चाहिए, डिग्री / एस, आदि)। संबंधित सेंसर की मनमानी इकाइयों में परिवर्तित करना अधिक सुविधाजनक है।सेंसर की मानक इकाइयों में एक निश्चित मूल्य की गणना कैसे करें?= * / ( — )
: 16- ±2g ?:
9,8 /2 * 65536 / (2g + 2g) = 9,8 /2 * 65536 / (2 * 9,8 /2 + 2 * 9,8 /2) = 16384 . . .
वैसे, यदि आप गेंद की त्रिज्या को ठीक से जानते हैं, तो आप केंद्र की "वेज" से ही गणना कर सकते हैं। यही है, उन बिंदुओं पर जो केवल गेंद की सतह के एक टुकड़े पर स्थित हैं। लेकिन यह हमारा मामला नहीं है।गेंद के केंद्र की खोज कैसे तेज करें?
केंद्र को पूरे घन (गेंद के आयाम) में नहीं देखना आवश्यक है, लेकिन रेखा के साथ, जिसकी शुरुआत मनमाना है, प्रत्येक अगला बिंदु वास्तविक केंद्र के करीब है और अंत केंद्र में है। मान लीजिए हम बिंदु से शुरू करते हैं (0; 0; 0) ... हम हमेशा एक स्थिर कदम के साथ आगे बढ़ते हैं। इसलिए, यदि हम 3x3x3 क्यूब्स के एक सेट की कल्पना करते हैं, जहां प्रत्येक चेहरा चरण आकार के बराबर है और यह भी कल्पना करता है कि वर्तमान स्थिति मध्य क्यूब है, तो हमारे पास 9 + 8 + 9 विकल्प हैं जहां अगला बिंदु डालना है। हमें बस प्रत्येक बिंदु पर होना है, यह गणना करने के लिए कि पड़ोसी में से 26 बिंदुओं में त्रुटि कम होगी। यदि यह पता चलता है कि त्रुटि वर्तमान बिंदु पर कम है, और पड़ोसी में से एक पर नहीं है, तो इसका मतलब है कि यह केंद्र में है और खोज खत्म हो गई है।
यह कोड में कैसे हो सकता हैPublic Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai, B + bi, C + ci, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
Exit Do
End If
A = A + ai_min
B = B + bi_min
C = C + ci_min
Loop
. . .
गेंद के केंद्र की खोज को गति देने के लिए और कैसे?
चर पिच के साथ खोजने की जरूरत है। पहले हम बड़े चरणों में केंद्र की तलाश करते हैं। हमने केंद्र पाया, हम कदम कम करते हैं और उसमें से हम आगे की खोज शुरू करते हैं। और इसी तरह, जब तक आपको आवश्यक सटीकता का परिणाम नहीं मिलता है।यह कोड में कैसे हो सकता हैPublic Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
step = 1000
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai * step, B + bi * step, C + ci * step, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
step = step / 10
If step < 0.01 Then
Exit Do
End If
Else
A = A + ai_min * step
B = B + bi_min * step
C = C + ci_min * step
End If
Loop
. . .
माप त्रुटियों के बारे में
माप के दौरान, ऐसी परिस्थितियां हो सकती हैं, जब किसी कारण से, गेंद की सतह से माप परिणाम बहुत दूर हो सकता है। या यह बहुत सारे बिंदु हो सकते हैं। या, सामान्य तौर पर, माप का परिणाम एक गेंद नहीं हो सकता है, लेकिन एक "अंडा" या एक "एयरशिप" हो सकता है। इस मामले में, निश्चित रूप से, आपको त्रुटियों के संभावित कारणों की पहचान करते हुए, सभी मापों को दोहराने की आवश्यकता है। उदाहरण के लिए, एक मैग्नेटोमीटर के लिए यह एक मेज में एक बोल्ट या एक कील हो सकता है और आप सीधे इसके ऊपर माप ले रहे हैं। और आप निचले हिस्से को मेरिडियन के साथ सेंसर को कम करते हैं, धातु जितना मजबूत होगा परिणाम को प्रभावित करेगा। इसलिए, एक स्वीकार्य त्रुटि मान की दहलीज निर्धारित करना आवश्यक है। कई स्पष्ट रूप से गलत बिंदुओं के कारण माप को फिर से न करने के लिए, आप एक फ़िल्टर लागू कर सकते हैं। फ़िल्टर का सिद्धांत बहुत सरल है - पहली बार केंद्र की गणना करने के बाद, उनमें से प्रत्येक में त्रुटि स्तर के आधार पर अंक सॉर्ट करें।सबसे बड़ी त्रुटि वाले कुछ बिंदुओं को आसानी से फेंक दिया जा सकता है (उदाहरण के लिए, 10%)। फिर आपको केंद्र की खोज को दोहराने की आवश्यकता है।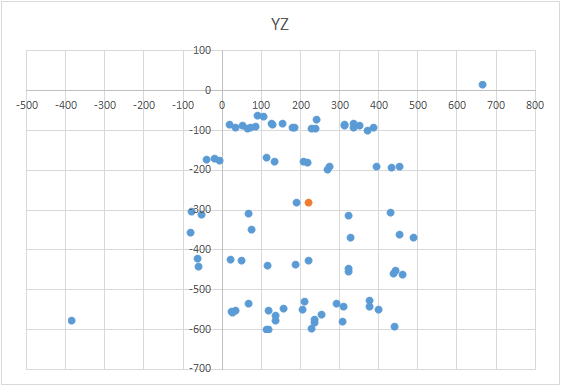
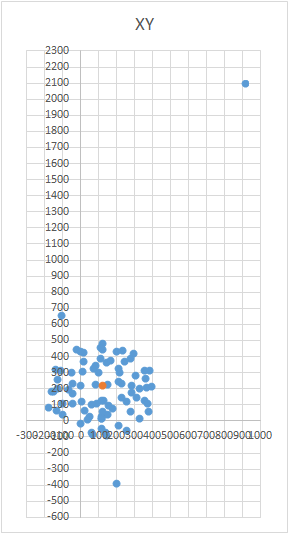
संपूर्ण
विधि में बहुत अच्छी सटीकता है। विधि आपको सरल तात्कालिक साधनों (गेंद, बैंक, आदि) के साथ करने की अनुमति देती है। यह काफी तेजी से काम करता है। सरल कोड। कई सेंसर में विशेष रजिस्टर होते हैं जहां आप पाया गया मान लिख सकते हैं, और सेंसर इसे मक्खी पर घटा देगा। इस तरह के रजिस्टरों में आमतौर पर उपसर्ग "TRIM" होता है, जैसा कि MPU9260, या "OFFSET" में, जैसा कि LSM303 में है। लेकिन सुप्रसिद्ध LIS302DL के पास ऐसे रजिस्टर नहीं हैं।अगर आपको यह पसंद आया तो एक प्लस साइन लगाना न भूलें। टिप्पणी में सेंसर को कैलिब्रेट करने के लिए अपने तरीके लिखें।