पिज्जा काटने के लिए वैज्ञानिकों ने नए तरीके ईजाद किए हैं

अपने नए काम में यूनिवर्सिटी ऑफ लिवरपूल के गणितज्ञों ने डिस्क को समान भागों में विभाजित करने के लिए कई पूर्व अज्ञात तरीकों को प्रकाशित किया । यह काम ज्यामिति के अनुभाग का है, तथाकथित अध्ययन लकड़ी की छत फर्श - अंतराल और ओवरलैप के बिना बहुभुज के साथ विमान की टाइलिंग। वैज्ञानिकों को पिज्जा काटने के तरीके खोजने के लिए प्रेरित किया गया था, एक प्रक्रिया जो हम में से अधिकांश के लिए परिचित थी।

जब ज्यामितीय आकृतियों (टाइल्स) के साथ विमान को झुकाते हैं, तो आप विभिन्न समस्याओं को सेट और हल कर सकते हैं। सबसे दिलचस्प कार्यों में से एक मोनोहेड्रल टाइलों का उपयोग है। इस मामले में, सभी टाइलों का आकार समान है, या, अधिक सटीक रूप से, बधाई हो। इसका मतलब है कि किसी भी दो टाइलों को आंदोलनों, घुमाव या दर्पण प्रतिबिंब की सहायता से जोड़ा जा सकता है।

प्लेन को बदलने के लिए उपयोग किए जाने वाले टाइल आकृतियों के सेट को प्रोटो-टाइल्स कहा जाता है। दिलचस्प बात यह है कि कोई गणितीय पद्धति नहीं है जो आपको पहले से बता सकती है कि दिए गए प्रोटोप्लेट्स की मदद से विमान को बदलना संभव है या नहीं। उदाहरण के लिए, यह ज्ञात है कि निम्नलिखित 24 में से एक हीरे (सात समबाहु त्रिभुजों से बनी आकृतियाँ ), केवल एक विमान के मोनोहाइड्रल टाइलिंग के लिए अनुपयुक्त है। लेकिन कौन सा?



इस मामले में - वी-आकार। लेकिन इसका प्रमाण कोई और नहीं बल्कि एक मामूली काम है।

हालांकि, लिवरपूल गणितज्ञों ने एक पूरे विमान के बजाय खुद को एक डिस्क तक सीमित कर लिया और डिस्क डिवीजन के लिए उपयुक्त मोनोहाइड्रल प्रोटो-टाइल्स की खोज शुरू कर दी। ऐसे प्रोटोप्लेट्स का एक संस्करण सभी को ज्ञात है। पिज्जा काटने की मानक विधि के साथ, इसे एक त्रिकोणीय आकार के बराबर खंडों में विभाजित किया जाता है, जिनमें से कोने डिस्क के केंद्र में परिवर्तित होते हैं। वैज्ञानिकों ने सवाल का जवाब देने का फैसला किया - क्या डिस्क के ऐसे विभाजन समान आंकड़ों में हैं जिनमें से ये सभी आंकड़े डिस्क के केंद्र को नहीं छूते हैं?

यही है, क्या पिज्जा को समान भागों में काटना संभव है, ताकि अधिक टॉपिंग पसंद करने वाले और अधिक क्रस्ट पसंद करने वाले दोनों को खुश किया जा सके? यह पता चला कि यह संभव है। इसके अलावा, इस तरह के काटने का एक संस्करण लंबे समय से जाना जाता है, और पेन्सिलवेनिया विश्वविद्यालय के समुदाय के लोगो पर स्थित है , जो छात्रों के लिए गणितीय सेमिनार आयोजित करता है: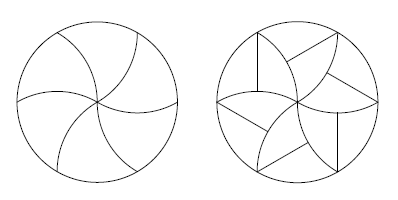



फिगर वाले स्लाइस को आधे में विभाजित किया जा सकता है, और सभी भागों को बधाई दी जाएगी, जिनमें से केवल आधा केंद्र को छूता है।

गणितज्ञों ने इस विचार को विकसित किया और एक डिस्क को विभाजित करने के अपने तरीकों को लगभग समान भागों में विभाजित किया।







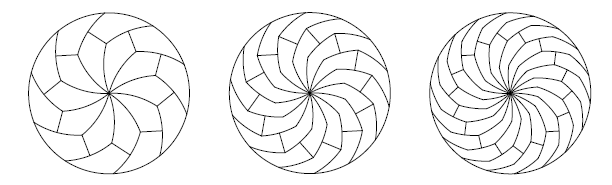जैसा कि गणित में अक्सर होता है, व्यवहार में काम के विचारों को लागू करने की संभावनाएं पूरी तरह से स्पष्ट नहीं हैं - जब तक कि एक गैर-मानक पिज्जा काटने वाले पिज्जा को प्रतिस्पर्धी लाभ के रूप में उपयोग न करें। लेकिन दूसरी ओर, यह अनुमान लगाने के लिए कि भविष्य में एक गणितीय खोज कैसे काम आएगी, यह भी असंभव है।

Source: https://habr.com/ru/post/hi389011/