आईटी विशेषज्ञ अनपेड रोड पर चलते हैं
दशकों के ठहराव के बाद, यात्रा सेल्समैन समस्या के लिए नए शॉर्टकट मिल गए हैं।
इतना समय पहले नहीं, स्टैनफोर्ड और मैकगिल विश्वविद्यालय के शोधकर्ताओं की एक टीम ने एक अकल्पनीय छोटी सी राशि से 35 साल के कंप्यूटर विज्ञान के रिकॉर्ड को तोड़ दिया - एक खरब खरब खरब के चार सौवें हिस्से से। सफलता - कंप्यूटर विज्ञान क्लासिक्स समस्या में एक सेल्समैन समस्या - किसी भी व्यावहारिक मूल्य के लिए बहुत छोटी थी, लेकिन उसने बेहतर अनुमानित समाधानों की तलाश में नए जीवन की सांस ली।कार्य निम्नानुसार बनता है: सड़कों से जुड़े शहरों के एक सेट के लिए, शुरुआती बिंदु पर लौटने के साथ प्रत्येक शहर की यात्रा के लिए सबसे छोटा रास्ता खोजना आवश्यक है। समस्या के समाधान में मुद्रित सर्किट बोर्डों में ड्रिलिंग छेद से व्यावहारिक अनुप्रयोग हैं जो कंप्यूटर पर कार्यों की अनुसूची का प्रबंधन करते हैं और जीनोम के गुणों को व्यवस्थित करते हैं।सेल्समैन समस्या को तैयार करना आसान है, और - सिद्धांत में - कम से कम खोजने के लिए सभी संभव बंद रास्तों की जांच करके हल करना आसान है। जानवर बल के दृष्टिकोण के साथ समस्या यह है कि जब शहरों की संख्या बढ़ती है, तो पथों की संगत संख्या बहुत तेजी से कंप्यूटर की क्षमताओं से अधिक होने लगती है। दस शहरों के लिए, 300,000 से अधिक मार्ग हैं। 15 शहरों के लिए, उनकी संख्या 87 बिलियन तक बढ़ जाती है।क्रिस्टोफ़ाइड्स एल्गोरिथ्म
प्रारंभिक कंप्यूटर युग में, गणितज्ञों को उम्मीद थी कि किसी को समस्या के लिए एक सुविधाजनक दृष्टिकोण मिलेगा - एक एल्गोरिथ्म जो इसे उचित समय में हल करने की अनुमति देता है। लेकिन यद्यपि प्रोग्रामरों ने विशिष्ट मामलों में प्रगति की - 1950 में 49 शहरों के लिए सबसे छोटे रास्ते का निर्धारण, 1980 के दशक में 2,392 शहरों के लिए और 2006 में 85,900 शहरों के लिए - किसी ने एक एल्गोरिथ्म का प्रस्ताव नहीं किया जो सामान्य मामले में समस्या को हल करता है। 1972 के उल्लेखनीय काम के अनुसार, यह संभव है कि इस तरह के एक एल्गोरिथ्म बिल्कुल मौजूद नहीं है। बर्कले में कैलिफोर्निया विश्वविद्यालय के कंप्यूटर वैज्ञानिक रिचर्ड कार्प ने दिखाया कि सेल्समैन समस्या एनपी-पूर्ण है, जिसका अर्थ है कि कोई कुशल एल्गोरिथ्म नहीं है (जब तक कि कोई भी यह साबित नहीं करता है कि पी = एनपी - लेकिन ज्यादातर वैज्ञानिक मानते हैं कि ऐसा नहीं है) ।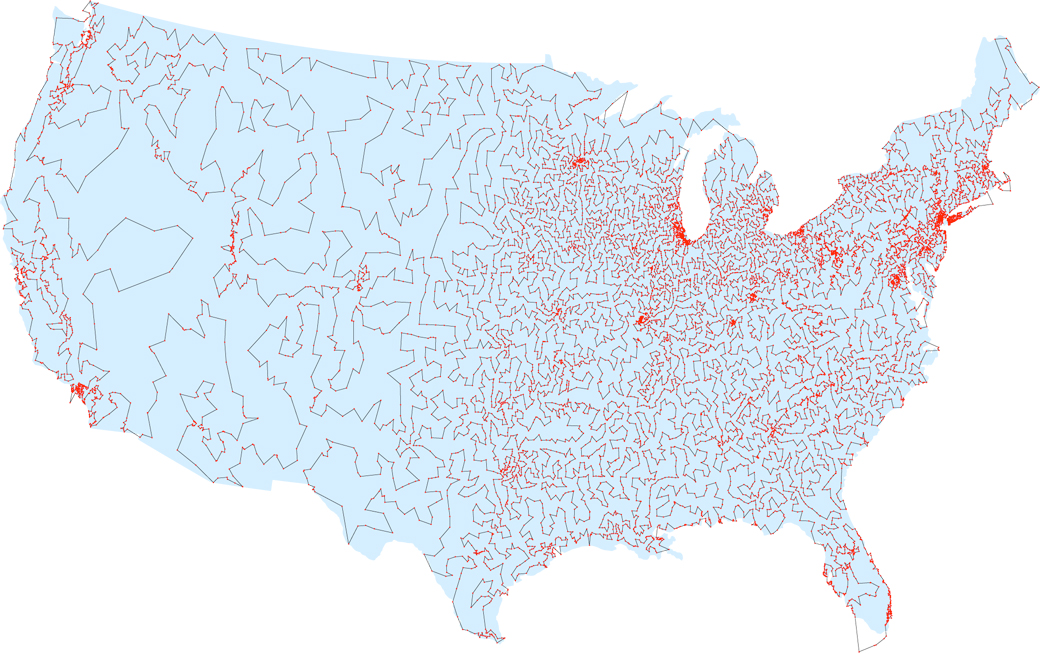
500 से अधिक आबादी (1998 के आंकड़ों के अनुसार) के साथ संयुक्त राज्य अमेरिका में सभी 13,509 शहरों के माध्यम से सबसे छोटा मार्ग, कार्प के प्रकाशन के बाद, कई कंप्यूटर वैज्ञानिकों ने समस्या के अनुमानित समाधानों को खोजने के लिए एक प्रभावी एल्गोरिदम विकसित करना शुरू कर दिया - बंद रास्ता जिसकी लंबाई सबसे कम से थोड़ी अधिक है। और यहां वे अधिक भाग्यशाली थे - 1976 में, इम्पीरियल कॉलेज लंदन के एक प्रोफेसर निकोस क्रिस्टोफ़ाइड्स ने एक एल्गोरिथ्म विकसित किया जो ऐसे पथ का निर्माण करता है जो 50% से अधिक कम से कम पथ से अधिक नहीं होने की गारंटी है।इसके निर्माण के बाद, कई वैज्ञानिकों ने फैसला किया कि यह एल्गोरिदम, जो छात्रों को एक घंटे में अध्ययन करने के लिए काफी सरल है, एक मध्यवर्ती लिंक बन जाएगा, जिसके बाद एक अधिक जटिल, बेहतर अनुमानित सच समाधान मिल जाएगा। लेकिन दशकों बाद, ऐसे एल्गोरिदम कभी नहीं दिखाई दिए।प्रिंसटन यूनिवर्सिटी के वैज्ञानिक संजीव अरोड़ा ने कहा, "लगभग सभी कंप्यूटर विज्ञान के छात्रों ने क्रिस्टोफ़ाइड्स के एल्गोरिथ्म को बेहतर बनाने के लिए हफ्तों या महीनों का समय बिताया।"अंत में, 2011 में, स्टैनफोर्ड और मैकगिल टीम कुछ प्रकार के सेल्समैन कार्यों के लिए 50% की गारंटी से आगे बढ़ गई और दिखाया कि उनका समाधान 49.9999999999999999999999999999999999999999999999696% से अधिक नहीं है।तब से, कई अनुमानित एल्गोरिदम दिखाई दिए हैं, जो समस्या पर नए सिरे से देखने के लिए धन्यवाद है। मैसाचुसेट्स इंस्टीट्यूट ऑफ टेक्नोलॉजी के एक आईटी विशेषज्ञ माइकल गोमांस के अनुसार, ये अनुमान केवल कुछ प्रकार के ट्रैवलिंग सेल्समैन कार्यों पर लागू होते हैं, लेकिन उनका दृष्टिकोण काफी आशाजनक है।"हम केवल सतह को थोड़ा छूते हैं," वे कहते हैं। "मुझे विश्वास है कि शायद पाँच वर्षों में, हम अधिक प्रभावशाली परिणाम प्राप्त करेंगे।"सबसे छोटा पेड़
100,000 शहरों के बीच एक मार्ग के रूप में मोना लिसा, क्रिस्टोफ़ाइड्स एल्गोरिथ्म सबसे छोटे रास्ते की खोज के साथ शुरू नहीं होता है, लेकिन कम से कम फैले हुए पेड़ की खोज के साथ - बंद लूप के बिना शहरों को जोड़ने वाली शाखाओं का एक सेट। सबसे छोटे रास्ते के विपरीत, न्यूनतम फैले हुए पेड़ का निर्माण करना काफी आसान है - आपको दो शहरों के बीच सबसे छोटे रास्ते की तलाश करके शुरू करने की आवश्यकता है; यह पहली शाखा होगी। निम्नलिखित को जोड़ने के लिए, आपको नए शहर और पिछले दो में से एक के बीच सबसे छोटा रास्ता खोजने की आवश्यकता है - और इसी तरह, जब तक कि सभी शहरों को कवर नहीं किया जाता है।परिणामी पेड़ यात्रा विक्रेता समस्या के संभावित समाधानों में से एक नहीं है, क्योंकि यह हमें एक बंद रास्ता नहीं देता है। लेकिन इसे ऐसे रास्ते में बदल दिया जा सकता है, जिसमें यह कल्पना की जाती है कि शाखाएं दीवारें हैं, और फिर पेड़ के साथ चलना ताकि आपकी उंगली दीवार को छूए जब तक आप शुरुआत में नहीं आते। परिणामी चलना प्रत्येक शहर से होकर गुजरता है और लौटता है, लेकिन आमतौर पर यह सबसे छोटे रास्ते से दूर होता है, क्योंकि यह एक ही खंड के साथ कई बार गुजरता है - हम प्रत्येक दीवार को एक पेड़ पर दो बार चलते हैं, एक बार प्रत्येक तरफ।लेकिन सबसे खराब स्थिति में परिणामी पथ दो बार सबसे छोटे मार्ग से अधिक नहीं है। विशेष रूप से चयनित शाखाओं को जोड़कर और कुछ तरकीबें लगाकर, क्रिस्टोफ़ाइड्स ने दिखाया कि इस रास्ते को कैसे काटा जाए ताकि यह कम से कम 50% से अधिक न हो।एक छोटा फैले पेड़ एक छोटे से वर्कअराउंड के निर्माण के लिए एक प्राकृतिक शुरुआती बिंदु है। लेकिन यह दृष्टिकोण एक क्रिस्टोफ़ाइड 50% गारंटी को निचोड़ने की कोशिश कर रहे शोधकर्ताओं के लिए एक शुरुआती बिंदु के रूप में भी कार्य करता है। सब के बाद, हालांकि पहली बार में एक न्यूनतम फैले हुए पेड़ प्रभावी दिखता है, अन्य पेड़ों को पेड़ों को एक वर्कअराउंड में परिवर्तित करने की प्रक्रिया के लिए बेहतर अनुकूल हो सकता है - उदाहरण के लिए, आपको शाखाओं के बिना एक पेड़ में केवल एक पैर जोड़ने की जरूरत है, ताकि यह वर्कअराउंड बन जाए।तो लक्ष्य एक ऐसे पेड़ को ढूंढना था जो लंबाई और सरल रूपांतरण के बीच संतुलन बनाता है। एक आदर्श पेड़ (यदि पी = एनपी सच नहीं है) की खोज के लिए कोई प्रभावी एल्गोरिदम नहीं हैं, लेकिन एक सफल अनुमानित एल्गोरिथ्म को केवल बहुत अच्छा खोजने की आवश्यकता है।भग्न यात्रा
"यथोचित रूप से अच्छे" पेड़ के रास्ते में एक लोकप्रिय, यद्यपि प्रतिवाद, तकनीक शामिल थी जो विशिष्ट कार्यों के लिए आंशिक समाधानों को मान्यता देती थी। उदाहरण के लिए, एक आंशिक वर्कअराउंड में मिनियापोलिस और डेट्रायट के बीच आधे रास्ते और क्लीवलैंड और डेट्रायट के बीच आधे रास्ते की यात्रा शामिल हो सकती है। व्यावहारिक दृष्टिकोण से, इस तरह के रास्ते का कोई मतलब नहीं है। लेकिन इसे गणितीय रूप से सटीक रूप से वर्णित किया जा सकता है, और क्लासिक ट्रैवलिंग सेल्समैन समस्या के विपरीत, इस तरह के एक आंशिक संस्करण को कुशलता से हल किया जा सकता है।कंप्यूटर विज्ञान में कई सन्निकटन समस्याओं को समस्या के आंशिक संस्करण के लिए समाधानों की गणना करके हल किया जा सकता है, और फिर मूल समस्या का अनुमानित समाधान प्राप्त करने के लिए शेयरों को समझदारी से गोल किया जा सकता है। लेकिन हाल तक तक, किसी ने भी यह पता नहीं लगाया था कि ट्रैवलिंग सेल्समैन की समस्या के मामले में ऐसा कैसे किया जाए।2009 में, स्टैनफोर्ड विश्वविद्यालय से अमीन सबेरी और फिर स्नातक छात्र, अरास असदपुर ने एक आम गोलाई योजना विकसित की जो एक पूर्णांक समाधान का चयन करने के लिए यादृच्छिक संख्याओं का उपयोग करती है जो संभव के रूप में आंशिक समाधान के कई गुणों को संरक्षित करती है। सबरी का मानना था कि यह पैटर्न "नाखून की तलाश में भारी हथौड़ा" की याद दिलाता है। और उन्हें संदेह था कि सेल्समैन का कार्य सही नाखून हो सकता है।कुछ महीनों बाद कृपाण, असदपुर, गोमांस, स्टैनफोर्ड स्नातक छात्र शायन घरान और अलेक्जेंडर मैड्री, जो अब स्विट्जरलैंड में लुसाने फेडरल पॉलिटेक्निक स्कूल में काम कर रहे हैं, ने दिखाया कि नई राउंडिंग तकनीक विकल्पों में से एक के लिए एक अच्छा अनुमानित एल्गोरिथ्म प्रदान कर सकती है। सेल्समैन के कार्य, "असममित" मामला। एक साल बाद, मैकगिल विश्वविद्यालय के कृपाण, गारन और मोहित सिंह ने समान यात्रा करने वाले सेल्समैन समस्या के लिए एक नया अनुमानित एल्गोरिदम विकसित करने के लिए एक ही दृष्टिकोण का उपयोग किया।
2006 में गणना की गई, 85,900 शहरों के बीच सबसे बड़ी सॉलिड ट्रैवल सेल्समैन समस्या थी। "शहरों" का स्थान बेल की प्रयोगशाला में निर्मित एक विशिष्ट कंप्यूटर चिप के डिजाइन से मेल खाता है, और इसका समाधान लेजर कटिंग का सबसे छोटा तरीका हैशहरों और मार्गों का एक नक्शा प्राप्त करने के बाद, नया एल्गोरिदम यात्रा सेल्समैन समस्या के सटीक आंशिक समाधान की गणना करके शुरू होता है। फिर वह इस घोल को एक फैले हुए वृक्ष के नीचे गिरा देता है, जो सैद्धांतिक रूप से लंबाई और सरल रूपांतरण के बीच संतुलन के करीब आना चाहिए। अंत में, एल्गोरिथ्म में यह पेड़ शामिल है - और न्यूनतम फैले हुए पेड़ - क्रिस्टोफ़ाइड्स नेटवर्क में नहीं।सबरी कहती हैं, "नया एल्गोरिथ्म एक ऐसा विचार था जिसे हम कुछ घंटों में समझा सकते थे, लेकिन इसका प्रमाण लगभग एक साल लगा।"एक लंबे विश्लेषण के बाद, स्टैनफोर्ड / मैकगिल टीम सेल्समैन कार्यों की एक विस्तृत उपवर्ग के लिए एक छोटे से अंश द्वारा क्रिस्टोफ़ाइड्स के एल्गोरिथ्म में सुधार करने में सक्षम थी, "ग्राफिक"। कुछ महीनों बाद, सफलता से प्रेरित अन्य टीमों ने ग्राफिक मामले के लिए बेहतर अनुमान लगाने के लिए एल्गोरिदम प्राप्त करने के लिए अन्य गोलाई योजनाओं का उपयोग किया। वर्तमान रिकॉर्ड 40% है, जो कि क्रिस्टोफ़ाइड के 50% से बहुत बेहतर है।अरोड़ा कहते हैं, "ग्राफिक समस्या" में सामान्य समस्याओं में से कई समान कठिनाइयाँ शामिल हैं, यह कहते हुए कि ग्राफिक मामले में काम करने वाली योजनाएँ सामान्य यात्रा विक्रेता समस्या के लिए भी उपयोगी हो सकती हैं।बहरहाल, कृपाण कहते हैं, सामान्य अनुमानित विक्रेता समस्या को हल करने के लिए नए विचारों की आवश्यकता होती है। “एक गणितीय खोज एक अंधेरे कमरे में जाने की तरह है। आप पहुंचते हैं और एक कुर्सी पाते हैं, पहुंचते हैं और एक मेज पाते हैं, '' वह कहते हैं, गणितज्ञ एंड्रयू विल्स को पैराफ्रेज करने के लिए। “कुछ बिंदु पर, हाथ एक स्विच पाता है, और अचानक सब कुछ स्पष्ट हो जाता है। सेल्समैन के कार्य के मामले में, इतने सारे कार्यों के बाद भी, जो संभव की इतनी सारी सीमाएँ पा चुका है, यह मुझे नहीं लगता कि हम पहले से ही इस स्विच को पा चुके हैं। "Source: https://habr.com/ru/post/hi399873/
All Articles