नवंबर में, क्वांटा पत्रिका ने अपने पाठकों को समान समतल वस्तुओं (जैसे सिक्के या डोमिनोज़) से आकृतियाँ बनाने के बारे में प्रश्नों के साथ विचलित किया। यह लेख प्रश्न और उनके विस्तृत उत्तर दोनों प्रदान करता है।प्रश्न 1
, , . . . , , ? n ?
शारीरिक रूप से, कार्य को तालिका के किनारे के दोनों किनारों पर आंकड़े के टॉर्क को संतुलित करने की आवश्यकता होती है। प्रत्येक पक्ष का टोक़ इस पक्ष के द्रव्यमान का उत्पाद है और द्रव्यमान के केंद्र से किनारे तक की दूरी है। जब पूरे आंकड़े के द्रव्यमान का केंद्र किनारे से ऊपर होता है, तो एक ही पल दोनों पक्षों पर कार्य करता है, और कुल सिस्टम टॉर्क शून्य होता है। एक यौगिक वस्तु के लिए, किसी भी चेहरे के लिए कुल टोक़ सभी घटकों के टोक़ को जोड़कर पाया जा सकता है। इसलिए, हम मूल कार्य पर विभाजित और शासन कर सकते हैं, केवल उन परिवर्तनों को देखते हुए जब एक मौजूदा स्टैक में एक नया ब्लॉक जोड़ा जाता है, कुछ गणितीय प्रेरण (इसे भौतिक प्रेरण कहते हैं)।एन -1 ब्लॉकों के ढेर पर विचार करें, जिनमें से प्रत्येक का वजन एक इकाई का होता है और जिसकी लंबाई एक इकाई होती है। तालिका के किनारे पर स्टैक संतुलित है। कल्पना करें कि दृष्टि की रेखा को तालिका के किनारे के साथ निर्देशित किया गया है, और तालिका बाईं तरफ है - अर्थात्, ब्लॉक के फांसी के छोर दाईं ओर फैलाए जाते हैं। चूंकि स्टैक किनारे पर संतुलित है, द्रव्यमान का केंद्र किनारे के ठीक ऊपर है, और इसका टोक़ शून्य है। अब कल्पना करें कि हमने पूरे स्टैक को लंबवत उठा लिया, और इसके नीचे एक और ब्लॉक रखा, ताकि इसका दाहिना किनारा टेबल के किनारे से फ्लश हो। व्यवहार में, यह मुश्किल हो सकता है, लेकिन एक विचार प्रयोग में यह सरल है।हमने नीचे से nth ब्लॉक जोड़कर स्टैक में कुछ स्थिरता दी, क्योंकि पूरे स्टैक के द्रव्यमान का केंद्र बाईं ओर थोड़ा स्थानांतरित हो गया। इस ऑफ़सेट x को अस्वीकृत करें। n ब्लॉक n इकाइयों का वजन करते हैं, और उनके पास टेबल के किनारे के आसपास एक सामान्य टोक़ x * n होता है, जिसे बाईं ओर निर्देशित किया जाता है। याद रखें कि n-1 ब्लॉकों के ढेर में कुल शून्य क्षण होता है। हमने केवल नए ब्लॉक का क्षण जोड़ा - एक द्रव्यमान की एक इकाई के साथ और तालिका के किनारे से द्रव्यमान के केंद्र की दूरी के साथ लंबाई की आधी इकाई।यह पता चलता है कि x * n = 1/2, जिसका अर्थ है x = 1 / 2n, जहां x तालिका के किनारे से द्रव्यमान के नए केंद्र की दूरी है।इसका मतलब है कि यदि आप लंबाई में 1/2 से n ब्लॉक के पूरे ढेर को दाईं ओर ले जाते हैं, तो यह किनारे पर पूरी तरह से संतुलित होगा - और यह अधिकतम संभव बदलाव है। प्रेरण के निर्माण को पूरा करने के लिए, हम ध्यान दें कि तालिका के किनारे से पहले ब्लॉक का अधिकतम ओवरहांग 1/2 इकाई लंबाई है।इसलिए, पांच ब्लॉकों के लिए, हम अधिकतम ओवरहांग प्राप्त करने के लिए 1 से पांच तक प्रत्येक स्तर के लिए सूत्र n में स्थानापन्न करते हैं:x=1/2+1/4+1/6+1/8+1/10=137/120=1,141(6)
यह देखा जा सकता है कि यदि आप ऊपर से शुरू करते हैं और फिर नीचे ब्लॉक जोड़ते हैं, तो प्रत्येक शिफ्ट उपलब्ध ब्लॉकों की संख्या के पारस्परिक का आधा होगा। व्युत्क्रम संख्याओं के ऐसे अनुक्रमों को हार्मोनिक श्रृंखला के रूप में जाना जाता है। इस तरह की श्रृंखला धीरे-धीरे विचलन करती है, और n के रूप में अनंत को जाता है, यह भी अनंत को जाता है।N ब्लॉकों के लिए सामान्य योग सूत्र श्रृंखला के सभी सदस्यों को संक्षेप में प्राप्त होता है। यह nth हार्मोनिक शब्द का आधा हिस्सा है, जिसे इस प्रकार लिखा जा सकता है:प्रश्न २
कल्पना करें कि आपके पास समान पांच ब्लॉक हैं, और आप उनमें से बहुत ऊपर कुछ सजावट रखना चाहते हैं, एक बिंदु पर जो फांसी के छोर से ब्लॉक की लंबाई का एक चौथाई है। सभी ब्लॉकों का वजन एक इकाई होता है, और गहने का वजन ब्लॉक का पांचवां होता है। अब ओवरहांग की अधिकतम लंबाई क्या है? यह मूल सूत्र को कैसे बदलता है?
सबसे पहले, उस पर खड़े सजावट के साथ पहले ब्लॉक पर विचार करें, और झूठ बोल रहा है ताकि इसका दाहिना किनारा तालिका के किनारे के साथ फ्लश हो। सजावट के बिना ब्लॉक के द्रव्यमान का केंद्र तालिका के किनारे से लंबाई की आधी इकाई है। सजावट इसे दाईं ओर ले जाएगी, एक्स द्वारा कहेंगे। सजावट का द्रव्यमान 1/5 है, और द्रव्यमान के नए केंद्र से इसकी दूरी 1/4 होगी। हम क्षणों को समान करते हैं और x = 1/5 * (1/4 x) प्राप्त करते हैं, इसलिए, x = 1/24। सजावट के कारण, लंबाई के 1/24 से पहले ब्लॉक को बाईं ओर स्थानांतरित करना आवश्यक है, इसलिए अधिकतम ओवरहांग अब 1/2 के बजाय 11/24 है।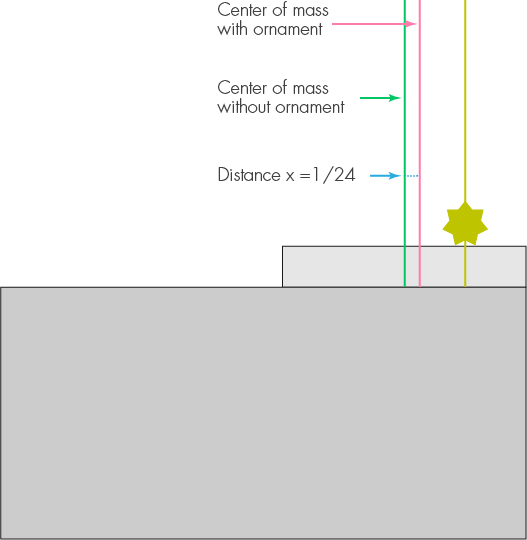
प्रश्न 3
, , . . . , . , , . , ?
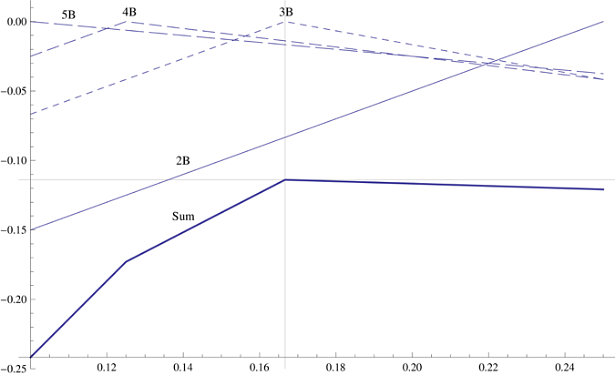
चूंकि दो से पांच ब्लॉक होने की संभावना समान है, इसलिए आपको इन चार मामलों के लिए अधिकतम ओवरहांग को दर्शाते हुए राशि को अधिकतम करने की आवश्यकता है। 2-5 ब्लॉकों के ढेर के लिए, पहले ब्लॉक का एक इष्टतम स्थान है, पूरे स्टैक का अधिकतम ओवरहांग देता है। यदि आप अगले स्टैक के चार संभावित आकारों में से प्रत्येक के लिए ग्राफ पर सबसे बड़ा ओवरहांग बनाते हैं, तो आपको एक उल्टे वी के रूप में दो लाइन ग्राफ और दो ग्राफ़ मिलते हैं। उनके कोने 3-4 ब्लॉकों के ढेर के लिए प्रारंभिक ब्लॉक की इष्टतम प्रारंभिक स्थिति को दर्शाते हैं। ग्राफ को समेटते हुए, हमें ओवरऑल ओवरफैंग ग्राफ मिलता है, जो नाटकीय रूप से चार इष्टतम पदों में से प्रत्येक में दिशा बदलता है। यह पता चला है कि तीन ब्लॉकों के लिए इष्टतम स्थिति में सबसे अच्छा समग्र ओवरहांग हासिल किया जाता है, जिसके बाद ग्राफ नीचे चला जाता है। इसलिए, आपको मूल ब्लॉक को धारणा के तहत रखने की आवश्यकता हैकि आपको तीन अतिरिक्त ब्लॉक दिए जाएंगे, और ओवरहांग लंबाई की 1/6 इकाई होगी।