असंभव वॉलपेपर कैसे बनाएं: निषिद्ध समरूपता का इतिहास

बाईं ओर एक वॉलपेपर पैटर्न है जिसमें भूरे-हरे रंग के रोसेट्स के चारों ओर छठे क्रम के रोटेशन समरूपता है। दाईं ओर एक वॉलपेपर पैटर्न है, जिसमें सना हुआ ग्लास विंडो टूर्नामेंट के प्रत्येक अण्डाकार तत्व के माध्यम से क्षैतिज रेखाओं के सापेक्ष दर्पण समरूपता है।

पहली नज़र में, वॉलपेपर का आविष्कार करना बालवाड़ी से कार्यों को पूरा करने से अधिक कठिन नहीं है। डिजाइनर मूल टुकड़े के लिए रंगों और आकृतियों के किसी भी संयोजन का चयन कर सकते हैं, और बस इसे दो दिशाओं में गुणा कर सकते हैं। प्रारंभिक टुकड़े के पैटर्न और निर्देशों की पसंद के आधार पर, अतिरिक्त समरूपताएं दिखाई दे सकती हैं - उदाहरण के लिए, पहली तस्वीर में छठे क्रम का समरूपता, या दूसरे में दर्पण समरूपता। दोनों पैटर्न कैलिफोर्निया विश्वविद्यालय के गणितज्ञ फ्रैंक फैरिस, सांता क्लारा द्वारा बनाए गए थे।


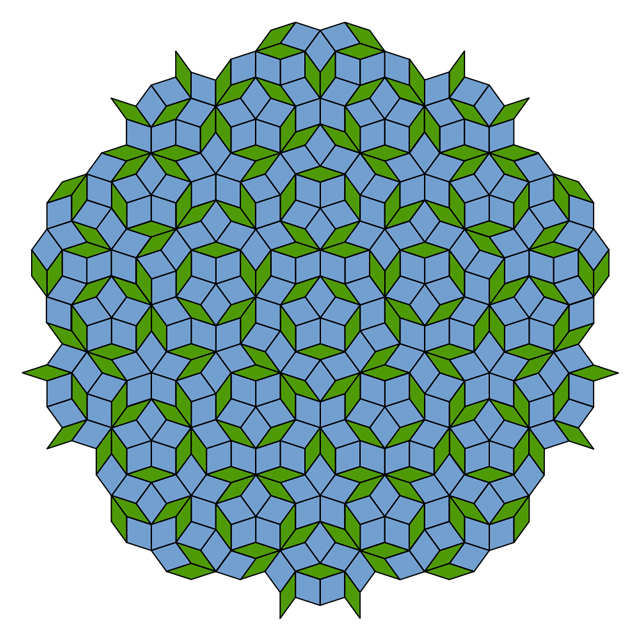पेनरोज़ टाइलें स्थानीय पांचवें क्रम के समरूपता के कई उदाहरण दिखाती हैं, लेकिन उनमें पैटर्न की पुनरावृत्ति नहीं होती है। विमान पर बड़े क्षेत्रों को भरते समय, चौड़ी टाइलों की संख्या संकीर्ण लोगों की संख्या का अनुपात सुनहरा अनुपात होता है।

लेकिन, हालांकि यह दूसरे, तीसरे, चौथे या छठे आदेशों के घूर्णी समरूपता के साथ वॉलपेपर बनाना संभव है, पांचवें क्रम के समरूपता के साथ वॉलपेपर बनाना असंभव है [आदेश से पता चलता है कि पैटर्न 360 सेकंड के रोटेशन के दौरान कितनी बार आत्म-संरेखित करेगा - लगभग। ट्रांस।]। यह प्रतिबंध लगभग 200 वर्षों के लिए गणितज्ञों को "क्रिस्टलोग्राफिक प्रतिबंध" के रूप में जाना जाता है। पांचवें-क्रम समरूपता के साथ पेंटागन की ज्यामिति पैटर्न को रोकती है। सात या अधिक के आदेश के लिए भी यही सच है।

हालांकि, सबसे दिलचस्प पैटर्न, जैसे कि पेनरोज़ टाइलें, कई स्थानों पर और विभिन्न पैमानों पर, बिना दोहराए केवल पैटर्न दोहराते हुए स्थानीय पांचवें क्रम की समरूपता दिखाती हैं। पेनरोस दृष्टिकोण से अलग एक विधि का उपयोग करते हुए, फैरिस ने असामान्य पांचवें क्रम के सममिति ज्यामिति पर अंकुश लगाया और रोमांचक छवियों का एक नया सेट बनाया - छद्म-वॉलपेपर जो पहली नज़र में, क्रिस्टलोग्राफिक बाधा नहीं मानते हैं।


अंजीर। 4

चतुर्थ आकृति क्रिस्टलोग्राफिक बाधा के लिए एक प्रतिरूप की तरह दिखती है, जिसमें बिंदु A के चारों ओर पांचवें क्रम के घूर्णी समरूपता होती है, जबकि पैटर्न को दिशा AB या AC में समतल पर स्थानांतरित किया जा सकता है। वास्तव में, फ़ारिस ने अमेरिकन मैथमेटिकल सोसाइटी के जर्नल नोटिसेस के लिए अपने लेख में लिखा है कि यह तस्वीर सिर्फ एक चतुर नकली है।

"आप जानते हैं कि आप जिस समरूपता का पालन करते हैं वह असंभव है," मिनेसोटा के कार्लटन कॉलेज के स्टीफन कैनेडी कहते हैं।

बिंदु ए के आसपास पांचवें क्रम के घूर्णी समरूपता पूरी होती दिख रही है। लेकिन अगर आप बारीकी से देखते हैं, तो आप देखेंगे कि बिंदु B और C के चारों ओर के पहिए A. से थोड़े अलग हैं। यदि हम पैटर्न से दूर जाकर और अधिक पुनरावृत्ति देख सकते हैं, तो पैटर्न के दृश्य पुनरावृत्ति बिंदु के क्षेत्र में एक पैटर्न की तरह कम और कम होंगे और, यहां तक ​​कि कभी भी ए की अधिक ठोस प्रतियां अन्य स्थानों पर दिखाई देंगी, जैसे कि अंजीर में। 5. फारिस ने दिखाया कि इस तरह के भ्रम को बड़े पैमाने पर भी बनाया जा सकता है, पैटर्न से दूर जाने और इसे एक निश्चित संख्या में दोहराते हुए - विशेष रूप से, फाइबोनैचि श्रृंखला (1, 1, 2, 3, 5, 8) से संख्याओं के अनुरूप। 13, 21, ... जहां प्रत्येक निम्नलिखित संख्या पिछले दो का योग है), जो पेनरोज टाइल्स की ज्यामिति में भी भूमिका निभाता है।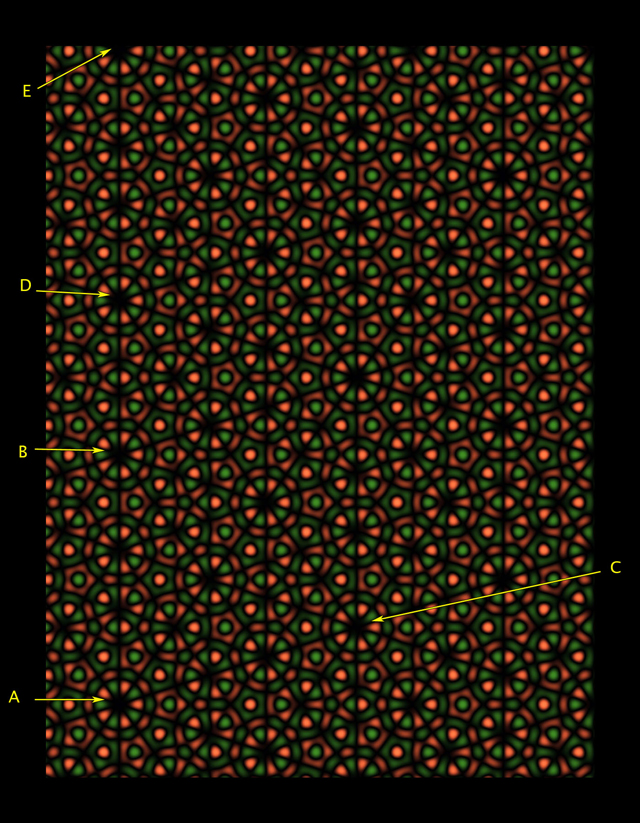


अंजीर। 5

फारिस कहती हैं, '' हम समझते हैं कि यह किसी तरह का धोखा है। फिर भी, जैसा कि वह लेख में लिखते हैं, ये चित्र "उन्हें पढ़ने के लिए हमारी आँखों को आमंत्रित करते हैं और लगभग पूर्ण पुनरावृत्ति का आनंद लेते हैं।"

फ़ारिस ने इन फेक के बारे में सोचा, जिस तकनीक को बदलकर उसने 3 डी क्रम के घूर्णी समरूपता के साथ वास्तविक वॉलपेपर बनाए, जैसे कि अंजीर में। 6।

3-क्रम समरूपता बनाने के लिए, फ़ारिस ने तीन-आयामी अंतरिक्ष में काम करना शुरू किया, जिसमें एक विशेष रूप से प्राकृतिक घुमाव है, जो तीन स्थानिक निर्देशांक के माध्यम से छंटनी करता है, और विकर्ण के चारों ओर अंतरिक्ष में 120 डिग्री घूमता है। फिर फ़ारिस ने तीन आयामी वॉलपेपर पैटर्न बनाए, विशेष रूप से चयनित साइनसोइड को सुपरइम्पोज़ करना और उन्हें पूर्व-चयनित रंग पैलेट के साथ संयोजन करना। अंक अधिरोपित साइनसोइड पर उनकी स्थिति के आधार पर दाग दिए गए थे। फिर फ़ारिस ने एक सपाट वॉलपेपर निकाला, इस रंग को एक दो आयामी विमान के लिए सीमित किया जो मूल स्थान के रोटेशन की धुरी के लंबवत है।

केनेडी कहते हैं, वॉलपेपर पैटर्न बनाने के लिए यह चिकनी, साइनसोइडल दृष्टिकोण पारंपरिक कॉपी और पेस्ट विधि से अलग है। "यह सममित पैटर्न बनाने के लिए एक बहुत ही नया तरीका है।"


अंजीर। 6

पांच-आयामी अंतरिक्ष में की गई एक ही प्रक्रिया, ऐसा लगता है, पांचवीं-क्रम समरूपता के साथ एक पैटर्न का निर्माण करना चाहिए था - अगर केवल हम नहीं जानते थे कि यह असंभव है। दिलचस्प बात यह है कि फारिस ने सोचा कि यह व्यवस्था किस बिंदु पर विफल है?

सैद्धांतिक रूप से, पांच आयामी स्थान संभव है, हालांकि यह कल्पना करना मुश्किल है। उनके पास पांचवें क्रम के रोटेशन की समरूपता का एक प्राकृतिक एनालॉग है, जैसा कि तीन आयामी अंतरिक्ष में है - तीसरे का समरूपता। पांच-आयामी अंतरिक्ष में, दो विमानों में से एक का चयन किया जा सकता है, जिनमें से प्रत्येक रोटेशन की धुरी और दूसरे विमान के लंबवत है। उनमें से प्रत्येक को एक बिंदु के आसपास 72 या 144 डिग्री से घुमाया जा सकता है। दो विमानों और एक-दूसरे के लिए सीधी रेखा की कल्पना करना मुश्किल लग सकता है, लेकिन पांच आयामों में इन सभी में पर्याप्त जगह है।

फ़ारिस ने इस समस्या को समझा - यदि एक सीधा विमान त्रि-आयामी अंतरिक्ष के माध्यम से सटीक रूप से कटता है और पूर्णांक निर्देशांक के साथ अनंत अंक वाले अनंत वॉलपेपर शामिल हैं, तो पांच-आयामी अंतरिक्ष में दो लंबवत विमान तर्कहीन हैं, और पूर्णांक निर्देशांक के साथ अंक नहीं हैं (संदर्भ बिंदु को छोड़कर) । चूंकि साइनसोइड से बने वॉलपेपर पैटर्न को पूर्णांक द्वारा पाली के माध्यम से दोहराया जाता है, ऐसे विमानों को उच्च-क्रम वाले स्थानों से पैटर्न विरासत में नहीं मिलते हैं।

"यह सूप में मक्खी कैसे दिखाई देता है," लेख में फारिस लिखते हैं।

फिर भी, वॉलपेपर की संरचना का भ्रम इन दोनों विमानों पर दिखाई देता है, तथाकथित की भागीदारी के लिए धन्यवाद सुनहरा अनुपात, एक अपरिमेय संख्या जो दो विमानों की दिशाओं और फाइबोनैचि संख्याओं का वर्णन करती है।

अपने संबंधों के लिए धन्यवाद, फ़ारिस यह दिखाने में कामयाब रहा कि हालांकि दो विमानों पर पूर्णांक निर्देशांक के साथ कोई बिंदु नहीं हैं, उनमें से प्रत्येक पूर्णांक निर्देशांक के साथ बिंदुओं के अंतहीन बिखरने के बहुत करीब आता है, जिनके निर्देशांक फाइबोनैचि संख्याएं हैं। जितनी बार विमान इन फाइबोनैचि बिंदुओं में से किसी एक पर पहुंचता है, पैटर्न संदर्भ बिंदु पर लगभग उतना ही दिखता है, जो एक सटीक प्रतिलिपि का भ्रम पैदा करता है।



फ़ारिस ने यह भी पता लगाया कि प्रकृति के फ़ोटो के रंगों और पैटर्नों को वेव फ़ंक्शंस के साथ कैसे पैटर्न के डिज़ाइन में शामिल किया जाए, जिसके परिणामस्वरूप आप बड़ी संख्या में "नकली" वॉलपेपर प्राप्त कर सकते हैं। उपरोक्त आंकड़े में, आप पेड़ों की शाखाओं को देख सकते हैं जो तस्वीर से विस्थापित हो गए हैं।

Source: https://habr.com/ru/post/hi400591/