विज्ञान में महत्वपूर्ण tautologies। भाग 1. भौतिकी
क्या आप जानते हैं कि लॉजिकल टॉटोलॉजी क्या है? आपको शायद पता हो। और यदि आप यह नहीं जानते हैं, तो लेखक इस अवधारणा को समझाने की कोशिश करेगा। हम गणित की सूखी और औपचारिक भाषा पर स्विच करना शुरू नहीं करेंगे, हम विकिपीडिया की तरह सौम्य पेडेंट नहीं होंगे, और हम कहेंगे कि आलंकारिक रूप से: एक टॉटोलॉजी एक प्रकार का ऑरोबोरोस है जो अपनी पूंछ को काटता है। उदाहरण के लिए, "कुछ भी नहीं है जब कुछ भी नहीं है", या, "ऐसी चीजें जो संकीर्ण और कम हैं जो इस द्वार से गुजरने के लिए आसानी से गुजरती हैं" और इसी तरह। इस तरह के बयान हमेशा सच होते हैं, और वे, मोटे तौर पर, कोई भी नई जानकारी नहीं देते हैं। हैरानी की बात है कि विज्ञान के कई महत्वपूर्ण कानूनों और सिद्धांतों में छिपे हुए ज्ञान हैं, जो हालांकि, उनके महत्व और शुद्धता से अलग नहीं होते हैं। रुचि रखते हैं? फिर कट के नीचे, आगे बढ़ो!सम्राट सरलाक ग्रांट स्केंटिकस III ऊब गया था। बहुत उबाऊ। आमतौर पर, जब वह ऊब महसूस करता था, तो वह पत्थर ( बल्कि सरल लेकिन मुश्किल खेल, हमारे चेकर्स, रिवर्सी और गो के लिए एक ही समय में समान ) खेलता था । हालाँकि, आज आमतौर पर उनके साथ खेलने वाले दार्शनिकों में से कोई भी नहीं आया। वह घूर कर बैठ गया और उसने एक स्थिति देखी।ग्रांट के आंतरिक प्रयोगकर्ता ने संभावित पदों की संख्या गिनने का निर्णय लिया। चलो इसे इस जगह पर छोड़ दें, और हमारी अपनी गिनती करें।नियमों के अनुसार, एक सेल पर 3 पत्थरों को रखने की अनुमति है। कुल 6 पत्थर हैं (प्रत्येक खिलाड़ी के लिए 3)। हम सभी संभावित पदों की संख्या पर विचार नहीं करेंगे। यह गणना करना अधिक दिलचस्प है कि आप कितने तरीकों से किसी पद को ले सकते हैं। लेकिन पहले, ड्राइंग को देखें।सादगी के लिए, हम केवल एक सेल पर विचार कर रहे हैं। उपरोक्त स्थिति, उदाहरण के लिए, ऐसे तीन तरीकों से प्राप्त की जा सकती है, जो बोर्ड में रखे गए पत्थरों से भिन्न होते हैं: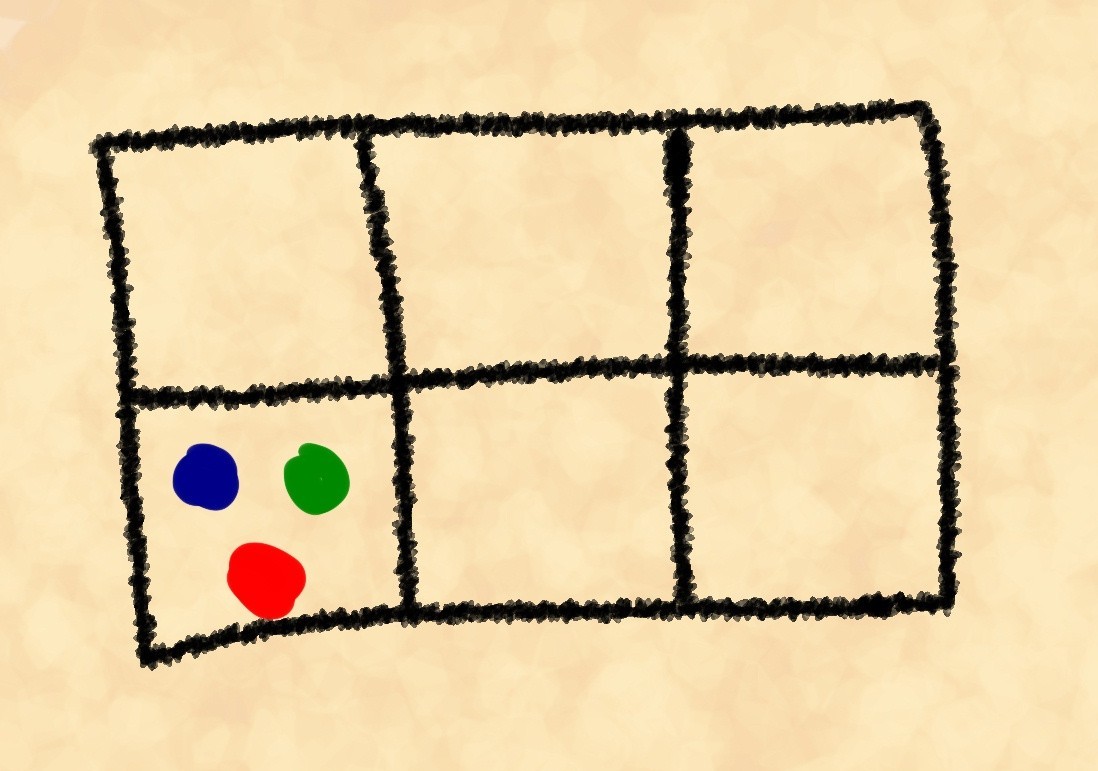

 हमने सशर्त रूप से पत्थरों को चित्रित किया ताकि हम उन्हें एक दूसरे से अलग कर सकें। जाहिर है, तीन से अधिक तरीके हैं। लेकिन वास्तव में कितना? तीन पत्थरों में से पहला हम छह तरीकों से चुन सकते हैं। इन छह विकल्पों में से प्रत्येक शेष पांच से दूसरे पत्थर की पसंद के साथ जारी है, और शेष चार में से अंतिम है। हमारे पास है। नतीजतन, हमारे पास आवश्यक तरीके से पत्थरों को बिछाने के लिए 120/6 = 20 तरीके हैं। आइए इस नंबर को इस स्थिति का वजन कहते हैं। बेशक, इसका शारीरिक वजन से कोई लेना-देना नहीं है, बस यह नाम आम तौर पर आंकड़ों में स्वीकार किया जाता है। आइए कार्य को जटिल करते हैं। आइए इन पदों के वजन की गणना करें:
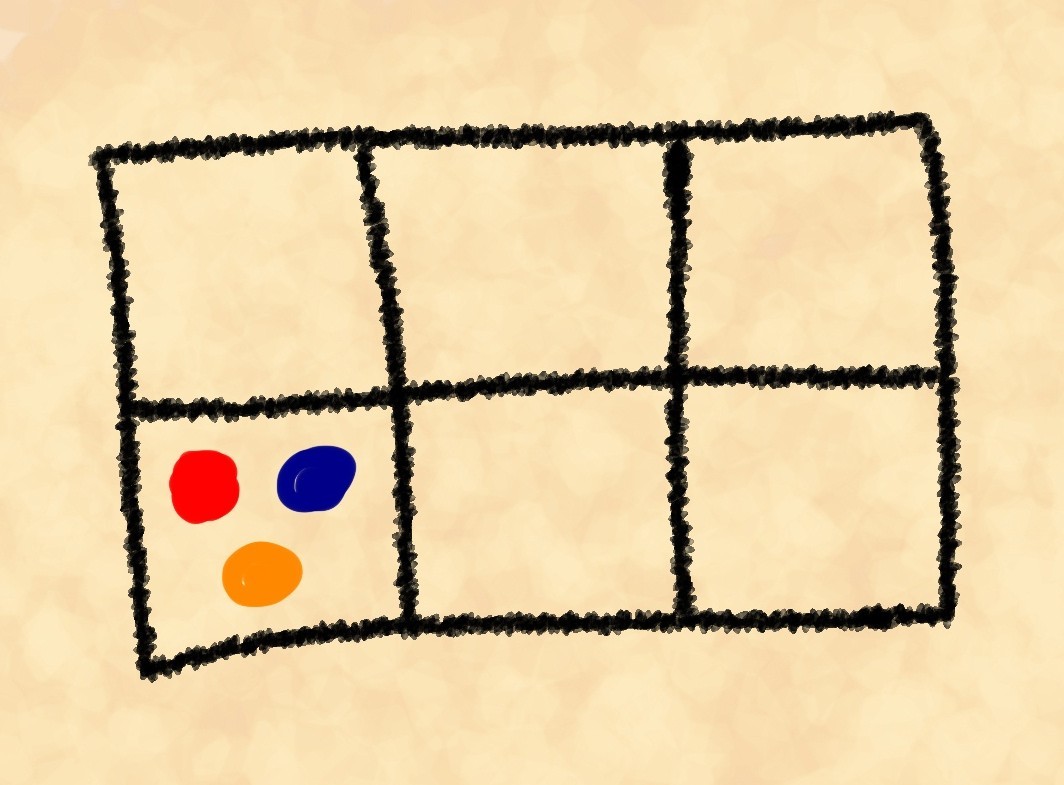
यदि आप इस सभी गणित को समझने के लिए बहुत आलसी हैं, तो अगले पैराग्राफ को छोड़ दें। पहली स्थिति:
हमने सशर्त रूप से पत्थरों को चित्रित किया ताकि हम उन्हें एक दूसरे से अलग कर सकें। जाहिर है, तीन से अधिक तरीके हैं। लेकिन वास्तव में कितना? तीन पत्थरों में से पहला हम छह तरीकों से चुन सकते हैं। इन छह विकल्पों में से प्रत्येक शेष पांच से दूसरे पत्थर की पसंद के साथ जारी है, और शेष चार में से अंतिम है। हमारे पास है। नतीजतन, हमारे पास आवश्यक तरीके से पत्थरों को बिछाने के लिए 120/6 = 20 तरीके हैं। आइए इस नंबर को इस स्थिति का वजन कहते हैं। बेशक, इसका शारीरिक वजन से कोई लेना-देना नहीं है, बस यह नाम आम तौर पर आंकड़ों में स्वीकार किया जाता है। आइए कार्य को जटिल करते हैं। आइए इन पदों के वजन की गणना करें:
यदि आप इस सभी गणित को समझने के लिए बहुत आलसी हैं, तो अगले पैराग्राफ को छोड़ दें। पहली स्थिति:


- हम दो बाईं कोशिकाओं में से एक पर 2 पत्थर फैलाते हैं:
- दूसरी कोशिका पर हम शेष 4 में से दो पत्थर बिछाते हैं:
- कुल हमारे पास है .
। सभी मामलों में विभाजन पुनरावृत्ति से छुटकारा पाने के लिए किया जाता है।तो, हमारे पास निम्नलिखित वजन हैं: पहले लेआउट के लिए 90, दूसरे के लिए 180 और तीसरे के लिए 360। क्या आपने देखा है कि स्थिति जितनी अधिक सुव्यवस्थित होगी, उसका वजन उतना ही कम होगा? महामहिम ग्रांट ने इस पर गौर किया। और अब वह वास्तविक गेमिंग पदों के लिए वजन की गणना करने जा रहा है।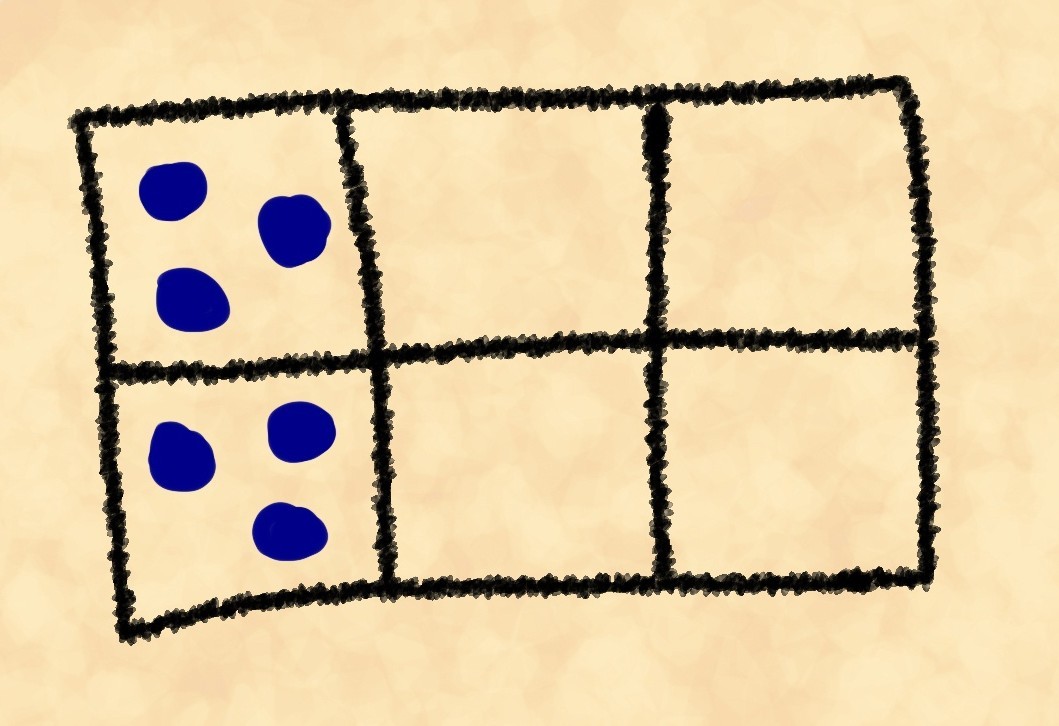

 वह क्रमशः 90, 360 और 720 बाहर निकलता है। हालांकि, यहां उसका धैर्य समाप्त हो जाता है (जैसे, शायद, आपका)। वह बोर्ड को परेशान करता है, पत्थरों को बेतरतीब ढंग से बिखेरता है, और दरवाजे पर खड़े दार्शनिक क्लोफ़ज़स को नोटिस करता है।"मुझे बताओ, दार्शनिक," वह असंतोष के एक नोट के साथ पूछता है, "क्यों, जब मैं बोर्ड को धक्का देता हूं, तो पत्थर इसके चारों ओर बेतरतीब ढंग से, समान रूप से उड़ते हैं, और किनारे से एक पिंजरे में तीन फिट नहीं होते हैं?क्लोफ़ियस ने इसके जवाब में मुस्कुराते हुए कहा:"मैंने कुछ समय के लिए आपकी गणना देखी, अधिपति, और आप शायद पहले से ही इस प्रश्न का उत्तर दे सकते हैं।" लेकिन मैं अभी भी कहता हूं - पत्थरों को बोर्ड के किनारे से नब्बे अलग-अलग तरीकों से ऑर्डर किया जा सकता है, और सभी कोशिकाओं में सात सौ बीस बिखरे जा सकते हैं। पत्थरों के लिए, किनारे पर समान रूप से एकत्र किए गए बोर्ड पर समान रूप से बिखरे हुए कई और तरीके हैं।शायद यहाँ हम सरलाक छोड़ देंगे। लेकिन क्लोफ़ज़स के स्पष्टीकरण पर ध्यान दें: पत्थर बोर्ड पर बिखरे हुए हैं क्योंकि उनके लिए एक समान तरीके से बिछाए जाने की तुलना में समान रूप से बिखरे हुए हैं। और तरीकों की संख्या के बीच का अंतर (पत्थरों के लेआउट का वजन) जितना अधिक होगा, उतना बड़ा बोर्ड और पत्थरों की संख्या। 15 कोशिकाओं (3 बाय 5) और 15 पत्थरों के बोर्ड के लिए, एक पूरी तरह से ऑर्डर किए गए लेआउट का वजन (एक किनारे के साथ 3 पत्थर प्रति सेल) लगभग 1.4 मिलियन (1,401,400 यदि ठीक है) और एक वर्दी के लिए (प्रत्येक सेल में एक) - लगभग 1.3 क्वाड्रिलियन , यानी लगभग एक लाख गुना ज्यादा। इसलिए, इस मामले में ऑर्डर प्राप्त करने की तुलना में गड़बड़ करना बहुत आसान है। एक अनजाने में इस तरह के एक अद्भुत बयान याद करते हैं: "अंडे हर कदम पर टूटते हैं, लेकिन किसी ने कभी नहीं देखा,ताकि एक टूटे हुए अंडे के टुकड़े एक साथ आए और एक पूरा अंडा बन जाए। और सभी क्योंकि पूरे अंडे प्राप्त करने का केवल एक ही तरीका है और असीम रूप से टूटने के कई तरीके हैं। ”हमने जो नियमितता पर ध्यान दिया है, उसे संक्षेप में प्रस्तुत करने के लिए:किसी भी प्रक्रिया में जो अपने आप होती है, बिना किसी अतिरिक्त बाहरी प्रभाव के, परिणाम जो सबसे बड़ी संख्या में प्राप्त किया जा सकता है, वह सबसे अधिक होने की संभावना है।बारीकी से देखें, तो यह इसकी सभी महिमाओं में से एक है। चीजों को सरल बनाने के लिए, मैं बस पुष्टि करता हूं कि "जो होना आसान है वह अधिक बार होता है।" हालांकि, यह सबसे महत्वपूर्ण शारीरिक कानूनों में से एक भी है। आप में से बहुत से लोग शायद पहले ही समझ चुके हैं कि हम ऊष्मप्रवैगिकी के दूसरे नियम के बारे में बात कर रहे हैं। आइए उनके "आधिकारिक" योगों मेंसे एक को देखें : एक बंद प्रणाली की प्रविष्टि कम नहीं हो सकती।अब यह एक तनातनी की तरह कम है, है ना? लेकिन किस तरह का चतुर शब्द एंट्रोपी है?आइए एक कमरे में हवा भरने की कल्पना करें। इसमें बड़ी संख्या में अणु होते हैं। अगर हम मानसिक रूप से कमरे को कोशिकाओं में विभाजित करते हैं, तो हमें बहुत बड़ी संख्या में पत्थरों के साथ पत्थरों के खेल का तीन आयामी एनालॉग मिलेगा। इस मामले में खेल की प्रत्येक स्थिति को सिस्टम का मैक्रोस्टेट कहा जाता है। पत्थरों के प्रत्येक लेआउट जो एक विशेष स्थिति को लागू करते हैं, एक माइक्रोस्टेट है । हम दो नंबर लेते हैं: सभी माइक्रोस्टेट की संख्या जो इस मैक्रोस्टेट को महसूस करती है और सभी संभावित माइक्रोस्टेट की संख्या। यदि हम पहले को दूसरे में विभाजित करते हैं, तो हम इस मैक्रोस्टेट की संभावना प्राप्त करेंगे।पुस्तक से परिभाषा: एक प्रणाली की स्थिति का एन्ट्रापी इस राज्य की संभावना का लघुगणक है।हम इसे एक ऐसी भाषा में अनुवादित करते हैं जिसे ग्रांट समझती है - किसी स्थिति की एन्ट्रापी किसी दिए गए स्थान के भार का लघुगणक है। आइए इसे और भी स्पष्ट करने का प्रयास करें: जितने अधिक तरीके से आप एक स्थिति प्राप्त कर सकते हैं, उतने ही एंट्रॉपी।अब हम देखते हैं कि दूसरे सिद्धांत का पुस्तक निरूपण निम्नलिखित कहता है: अपने आप में एक स्थिति से, केवल उस स्थिति के लिए एक संक्रमण जो अधिक से अधिक या एक ही पथ के साथ प्राप्त किया जा सकता है क्योंकि प्रारंभिक एक हो सकता है।आइए इसे सरल बनाने का प्रयास करें: यदि हम बोर्ड को हिलाते हैं, तो हम जल्द ही एक ऐसा स्थान प्राप्त करेंगे जो प्राप्त करना आसान है।ऐसा लगता है कि हम फिर से तनातनी पर उतर आए हैं। हालांकि, भले ही यह एक तनातनी है, दूसरा सिद्धांत सबसे महत्वपूर्ण भौतिक कानूनों में से एक है। इसके अलावा, यह भौतिकी का एकमात्र नियम है जो हमें बताता है कि समय एक निश्चित दिशा में प्रवाहित होना चाहिए, जो अतीत और भविष्य के बीच अंतर करता है।अंत में, आइए दूसरी शुरुआत के कुछ और सूत्र देखें:
वह क्रमशः 90, 360 और 720 बाहर निकलता है। हालांकि, यहां उसका धैर्य समाप्त हो जाता है (जैसे, शायद, आपका)। वह बोर्ड को परेशान करता है, पत्थरों को बेतरतीब ढंग से बिखेरता है, और दरवाजे पर खड़े दार्शनिक क्लोफ़ज़स को नोटिस करता है।"मुझे बताओ, दार्शनिक," वह असंतोष के एक नोट के साथ पूछता है, "क्यों, जब मैं बोर्ड को धक्का देता हूं, तो पत्थर इसके चारों ओर बेतरतीब ढंग से, समान रूप से उड़ते हैं, और किनारे से एक पिंजरे में तीन फिट नहीं होते हैं?क्लोफ़ियस ने इसके जवाब में मुस्कुराते हुए कहा:"मैंने कुछ समय के लिए आपकी गणना देखी, अधिपति, और आप शायद पहले से ही इस प्रश्न का उत्तर दे सकते हैं।" लेकिन मैं अभी भी कहता हूं - पत्थरों को बोर्ड के किनारे से नब्बे अलग-अलग तरीकों से ऑर्डर किया जा सकता है, और सभी कोशिकाओं में सात सौ बीस बिखरे जा सकते हैं। पत्थरों के लिए, किनारे पर समान रूप से एकत्र किए गए बोर्ड पर समान रूप से बिखरे हुए कई और तरीके हैं।शायद यहाँ हम सरलाक छोड़ देंगे। लेकिन क्लोफ़ज़स के स्पष्टीकरण पर ध्यान दें: पत्थर बोर्ड पर बिखरे हुए हैं क्योंकि उनके लिए एक समान तरीके से बिछाए जाने की तुलना में समान रूप से बिखरे हुए हैं। और तरीकों की संख्या के बीच का अंतर (पत्थरों के लेआउट का वजन) जितना अधिक होगा, उतना बड़ा बोर्ड और पत्थरों की संख्या। 15 कोशिकाओं (3 बाय 5) और 15 पत्थरों के बोर्ड के लिए, एक पूरी तरह से ऑर्डर किए गए लेआउट का वजन (एक किनारे के साथ 3 पत्थर प्रति सेल) लगभग 1.4 मिलियन (1,401,400 यदि ठीक है) और एक वर्दी के लिए (प्रत्येक सेल में एक) - लगभग 1.3 क्वाड्रिलियन , यानी लगभग एक लाख गुना ज्यादा। इसलिए, इस मामले में ऑर्डर प्राप्त करने की तुलना में गड़बड़ करना बहुत आसान है। एक अनजाने में इस तरह के एक अद्भुत बयान याद करते हैं: "अंडे हर कदम पर टूटते हैं, लेकिन किसी ने कभी नहीं देखा,ताकि एक टूटे हुए अंडे के टुकड़े एक साथ आए और एक पूरा अंडा बन जाए। और सभी क्योंकि पूरे अंडे प्राप्त करने का केवल एक ही तरीका है और असीम रूप से टूटने के कई तरीके हैं। ”हमने जो नियमितता पर ध्यान दिया है, उसे संक्षेप में प्रस्तुत करने के लिए:किसी भी प्रक्रिया में जो अपने आप होती है, बिना किसी अतिरिक्त बाहरी प्रभाव के, परिणाम जो सबसे बड़ी संख्या में प्राप्त किया जा सकता है, वह सबसे अधिक होने की संभावना है।बारीकी से देखें, तो यह इसकी सभी महिमाओं में से एक है। चीजों को सरल बनाने के लिए, मैं बस पुष्टि करता हूं कि "जो होना आसान है वह अधिक बार होता है।" हालांकि, यह सबसे महत्वपूर्ण शारीरिक कानूनों में से एक भी है। आप में से बहुत से लोग शायद पहले ही समझ चुके हैं कि हम ऊष्मप्रवैगिकी के दूसरे नियम के बारे में बात कर रहे हैं। आइए उनके "आधिकारिक" योगों मेंसे एक को देखें : एक बंद प्रणाली की प्रविष्टि कम नहीं हो सकती।अब यह एक तनातनी की तरह कम है, है ना? लेकिन किस तरह का चतुर शब्द एंट्रोपी है?आइए एक कमरे में हवा भरने की कल्पना करें। इसमें बड़ी संख्या में अणु होते हैं। अगर हम मानसिक रूप से कमरे को कोशिकाओं में विभाजित करते हैं, तो हमें बहुत बड़ी संख्या में पत्थरों के साथ पत्थरों के खेल का तीन आयामी एनालॉग मिलेगा। इस मामले में खेल की प्रत्येक स्थिति को सिस्टम का मैक्रोस्टेट कहा जाता है। पत्थरों के प्रत्येक लेआउट जो एक विशेष स्थिति को लागू करते हैं, एक माइक्रोस्टेट है । हम दो नंबर लेते हैं: सभी माइक्रोस्टेट की संख्या जो इस मैक्रोस्टेट को महसूस करती है और सभी संभावित माइक्रोस्टेट की संख्या। यदि हम पहले को दूसरे में विभाजित करते हैं, तो हम इस मैक्रोस्टेट की संभावना प्राप्त करेंगे।पुस्तक से परिभाषा: एक प्रणाली की स्थिति का एन्ट्रापी इस राज्य की संभावना का लघुगणक है।हम इसे एक ऐसी भाषा में अनुवादित करते हैं जिसे ग्रांट समझती है - किसी स्थिति की एन्ट्रापी किसी दिए गए स्थान के भार का लघुगणक है। आइए इसे और भी स्पष्ट करने का प्रयास करें: जितने अधिक तरीके से आप एक स्थिति प्राप्त कर सकते हैं, उतने ही एंट्रॉपी।अब हम देखते हैं कि दूसरे सिद्धांत का पुस्तक निरूपण निम्नलिखित कहता है: अपने आप में एक स्थिति से, केवल उस स्थिति के लिए एक संक्रमण जो अधिक से अधिक या एक ही पथ के साथ प्राप्त किया जा सकता है क्योंकि प्रारंभिक एक हो सकता है।आइए इसे सरल बनाने का प्रयास करें: यदि हम बोर्ड को हिलाते हैं, तो हम जल्द ही एक ऐसा स्थान प्राप्त करेंगे जो प्राप्त करना आसान है।ऐसा लगता है कि हम फिर से तनातनी पर उतर आए हैं। हालांकि, भले ही यह एक तनातनी है, दूसरा सिद्धांत सबसे महत्वपूर्ण भौतिक कानूनों में से एक है। इसके अलावा, यह भौतिकी का एकमात्र नियम है जो हमें बताता है कि समय एक निश्चित दिशा में प्रवाहित होना चाहिए, जो अतीत और भविष्य के बीच अंतर करता है।अंत में, आइए दूसरी शुरुआत के कुछ और सूत्र देखें:- क्लॉजियस आसन: एक परिपत्र प्रक्रिया असंभव है, जिसका एकमात्र परिणाम एक कम गर्म शरीर से एक गर्म तक गर्मी का हस्तांतरण है।
- थॉमसन का संकेत: एक परिपत्र प्रक्रिया असंभव है, जिसका एकमात्र परिणाम गर्मी जलाशय को ठंडा करके काम का उत्पादन होगा।
जैसा कि आप देख सकते हैं, अब एक तनातनी नहीं है। और उनमें से एक भी स्पष्ट नहीं है। हालाँकि, यह दिखाया जा सकता है कि ये दोनों सूत्रीकरण "पूरी तरह से समसामयिक के बराबर हैं" यह सबसे अधिक संभावना है कि कुछ अधिक होने की संभावना है "। कभी-कभी कुछ नया सीखने के लिए, हमें सबसे पहले कुछ स्पष्ट करने की आवश्यकता होती है।अगले भाग में, हम एक और "वैज्ञानिक तानशास्त्र" पर विचार करेंगे, जो पहली नज़र में, ऊष्मप्रवैगिकी के दूसरे नियम का उल्लंघन करता है। Source: https://habr.com/ru/post/hi400803/
All Articles