“एक ही तापमान पर दो समान गेंदें हैं। उनमें से एक क्षैतिज सतह पर स्थित है, दूसरा एक धागे पर निलंबित है। दोनों गेंदें समान मात्रा में गर्मी की सूचना देती हैं। क्या इसके बाद गेंदें समान होंगी या नहीं? (किसी भी तरह की गर्मी के नुकसान की उपेक्षा की जा सकती है।)

इस तरह की समस्या कभी-कभी भौतिकी और सोशल मीडिया ओलंपियाड्स में पाई जा सकती है। आम तौर पर स्वीकृत जवाब सहज है: गुरुत्वाकर्षण की उपस्थिति में थर्मल विस्तार के लिए ऊर्जा की खपत के कारण, एक क्षैतिज सतह पर पड़ी एक गेंद एक धागे पर लटकाए जाने से अधिक ठंडी होगी। हाल के एक लेख से पता चला है कि यह उत्तर गलत है। वास्तव में, परिणाम विपरीत होगा: झूठ बोलने वाली गेंद फांसी की तुलना में गर्म होगी। हम समझेंगे कि इस समस्या को हल करने का पारंपरिक तरीका गलत उत्तर की ओर क्यों जाता है, और इस मामले में अंतर्ज्ञान हमें नीचे क्यों लाता है।

पारंपरिक समाधान और इसकी समस्या

पारंपरिक समाधान तर्क की निम्नलिखित पंक्ति पर आधारित है। हीटिंग के दौरान दोनों गेंदों का विस्तार होगा, इस वजह से क्षैतिज सतह पर पड़ी गेंद के द्रव्यमान का केंद्र थोड़ा बढ़ जाएगा, और गेंद के लटकने के द्रव्यमान का केंद्र गिर जाएगा। नतीजतन, लेटी हुई गेंद कमजोर हो जाती है, क्योंकि इसमें स्थानांतरित होने वाली गर्मी के हिस्से को इसके उत्थान पर खर्च किया जाएगा, और लटकने वाली गेंद गुरुत्वाकर्षण के अतिरिक्त काम के कारण कम हो जाएगी।


पारंपरिक समाधान में इस्तेमाल की जाने वाली रीज़निंग: थर्मल विस्तार के कारण, टेबल पर पड़ी गेंद उठती है, और धागे पर लटकी हुई गेंद को नीचे लाया जाता है।

उत्तर झूठ के तापमान के अंतर के लिए एक सरल सूत्र द्वारा व्यक्त किया जा सकता है ( $$ ) और फांसी ( $$ ) गेंदें:

$$

जहाँ $$ । $$ और $$ - जन, त्रिज्या और गेंदों की गर्मी क्षमता, $$ - उन्हें हस्तांतरित गर्मी की मात्रा, $$ - गुरुत्वाकर्षण का त्वरण, $$ गेंदों की सामग्री के रैखिक थर्मल विस्तार का गुणांक है , जिसे हम पर्याप्त रूप से छोटा मानते हैं। जैसा देखा है $$ - लेट बॉल ज्यादा ठंडी होगी।

ऐसा लगता है कि इस निर्णय में सब कुछ तर्कसंगत है। "पहली निगल", यह दर्शाता है कि यहां कुछ गलत है, गेंद के आधार पर एक गर्मी इंजन बनाने का एक मानसिक प्रयास है।

मशीन निम्नानुसार काम कर सकती है: सबसे पहले, गेंद मेज पर होती है, जहां हम इसे गर्म करते हैं, जिसके कारण इसका द्रव्यमान का केंद्र बढ़ जाता है। फिर हम शीर्ष पर लटके हुए धागे पर गेंद को ठीक करते हैं और मेज को ध्यान से हटाते हैं ताकि गेंद की ऊंचाई में बदलाव न हो। अंत में, हम गेंद को उसके शुरुआती तापमान पर ठंडा करते हैं, परिणामस्वरूप, गेंद संकुचित होती है और इसका द्रव्यमान बढ़ जाता है। नीचे की रेखा: गर्मी का वह हिस्सा जिसे हम गेंद में स्थानांतरित करते हैं जब इसे गर्म किया जाता था, इसे उठाने के लिए इसे यांत्रिक कार्य में बदल दिया जाता था और इस चक्र को अंतहीन रूप से दोहराया जा सकता है।


एक गेंद-आधारित गर्मी इंजन के संचालन का चक्र: हीटिंग और शीतलन के बाद, गेंद गुलाब हुई, जिसका अर्थ है कि हमने यांत्रिक कार्यों में गर्मी का हिस्सा बदल दिया।

यहां समस्या यह है कि गेंद की त्रिज्या को बढ़ाकर, इस तरह की मशीन की दक्षता (दक्षता) 100% के करीब मनमाने ढंग से बनाई जा सकती है। यह ऊष्मागतिकी के दूसरे नियम का खंडन करता है, जिसके अनुसार हीटर और रेफ्रिजरेटर के समान तापमान पर हीट इंजन की दक्षता कारनोट चक्र की क्षमता से अधिक नहीं हो सकती।

मामला क्या है?

समस्या का पारंपरिक समाधान गलत क्यों है? यहां यह ध्यान रखना आवश्यक है कि गेंद को शुरुआत से ही मेज पर लेटा दिया जाए, गर्म होने से पहले, गुरुत्वाकर्षण से थोड़ा चपटा होगा, और लटकी हुई गेंद को थोड़ा फैलाया जाएगा। यह ऊपर वर्णित गर्मी इंजन की दक्षता को नकारात्मक रूप से प्रभावित करेगा: निलंबन के दौरान, गेंद थोड़ी कम हो जाएगी, इस वजह से दक्षता कम हो जाएगी और कारनोट चक्र की दक्षता से अधिक नहीं होगी।


गेंदों पर गुरुत्वाकर्षण का प्रभाव: मेज पर पड़ी हुई गेंद चपटी होती है, और धागे पर लटका हुआ एक खिंचाव होता है।

मूल समस्या पर विचार करने पर यह कैसे प्रकट होगा? यह पता चलता है कि किसी सामग्री को संपीड़ित करने या खींचने से उसकी ऊष्मा क्षमता में परिवर्तन होता है: संपीड़ित सामग्री के मामले में, एक ही तापमान पर गर्म होने पर एक खिंचाव वाली स्थिति की तुलना में कम गर्मी की आवश्यकता होगी। इसलिए:

• जब मेज पर पड़ी गेंद को गर्म किया जाता है, तो ऊष्मीय विस्तार के कारण ऊष्मा का हिस्सा अपने उत्थान में चला जाएगा; लेकिन, इसके साथ-साथ, बॉल मटेरियल को गर्म करना अपने आप आसान हो जाएगा और कम गर्मी की आवश्यकता होगी।
• जब एक धागे पर लटकी हुई गेंद को गर्म किया जाता है, तो जब इसे उतारा जाता है, तो गुरुत्वाकर्षण का काम इसमें स्थानांतरित होने वाली गर्मी में जुड़ जाएगा; लेकिन, इसके साथ-साथ, बॉल मटेरियल को गर्म करना अधिक समय लेने वाला होगा और अधिक गर्मी की आवश्यकता होगी।

पारंपरिक समाधान में, सफेद तीर द्वारा इंगित केवल कारकों को ध्यान में रखा जाता है। काले तीर द्वारा दिखाए गए कारकों को अनदेखा करना एक गलत जवाब है।

जैसा कि हम देख सकते हैं, दोनों ही मामलों में ऐसे कारक हैं जो एक उत्तर विकल्प के पक्ष में दोनों काम करते हैं (एक लेटी हुई गेंद एक हैंगिंग की तुलना में अधिक ठंडी हो सकती है) और विपरीत दिशा में (एक लेट बॉल एक हैंगिंग की तुलना में गर्म हो सकती है)। कौन सा ओवरपॉवर करता है?

ऐसा लगता है कि संपीड़न या तनाव के दौरान एक सामग्री की गर्मी क्षमता को बदलने का प्रभाव, भले ही यह मौजूद हो, बहुत छोटा होना चाहिए, और इसे उपेक्षित किया जा सकता है, जैसा कि समस्या के पारंपरिक समाधान में किया जाता है। हालाँकि, ऐसा नहीं है। यह प्रभाव अपने आप में थर्मल विस्तार के रूप में लघुता के उसी क्रम का है, क्योंकि ये दोनों प्रभाव अंतर-धार्मिक शक्तियों की धार्मिकता से उपजा है। इन प्रभावों में से एक को ध्यान में रखते हुए पारंपरिक समाधान में अन्य की अनदेखी के साथ असंगत है और एक गलत उत्तर की ओर जाता है।

लेख से पता चलता है कि समस्या के सही समाधान के साथ, उतनी ही मात्रा में गर्मी के बाद गेंदों का तापमान अंतर उनके बराबर है:

$$

जहाँ $$ - गेंदों का पूर्ण तापमान, $$ - उसके तापमान में बदलाव के साथ गेंदों की सामग्री के थर्मल विस्तार के गुणांक के परिवर्तन की दर।

पारंपरिक समाधान के परिणाम की तुलना में, तापमान में अंतर है:

• विपरीत चिन्ह, चूंकि अधिकांश सामग्रियों का मूल्य है $$ सकारात्मक है, इसलिए समानता का संपूर्ण दाहिना पक्ष भी सकारात्मक है, और $$ ।
• निरपेक्ष मूल्य में बहुत छोटा है, क्योंकि यहां एक छोटे से मूल्य के बजाय छोटे मूल्य भी दिखाई देते हैं $$ और $$ ।

इस प्रकार, ऊपर वर्णित दो प्रभाव लगभग पूरी तरह से एक दूसरे को रद्द कर देते हैं, लेकिन उनमें से दूसरा (संपीड़न या तनाव के दौरान गर्मी क्षमता में परिवर्तन) पहले (थर्मल विस्तार) की तुलना में थोड़ा मजबूत है।

अंतर-ताकतों की धार्मिकता

लेख के लेखक समस्या के बारे में अधिक कठोर विचार करते हैं, लेकिन, दुर्भाग्यवश, यह स्पष्ट विवरण नहीं देते हैं कि दोनों प्रभावों का लगभग पूरा मुआवजा कैसे होता है, इसलिए मुझे इसका पता लगाना था।

यह आंकड़ा उनके बीच की दूरी पर परमाणु संपर्क की संभावित ऊर्जा की एक विशिष्ट निर्भरता को दर्शाता है। परमाणुओं पर कार्य करने वाला बल संभावित ऊर्जा में कमी की ओर निर्देशित होता है, इसलिए, परमाणु एक दूसरे को छोटी दूरी पर दृढ़ता से पीछे हटा देते हैं और बड़ी दूरी पर कमजोर रूप से आकर्षित होते हैं। कुछ दूरी पर $$ संभावित ऊर्जा न्यूनतम तक पहुँचती है। सबसे ऊर्जावान रूप से लाभप्रद दूरी के लिए परमाणुओं की इच्छा उनके अणुओं, तरल पदार्थों और ठोस पदार्थों के लिए बाध्य होने का कारण है।


अब देखते हैं कि सामग्रियों का थर्मल विस्तार कहां से आता है। अराजक थर्मल गति के साथ, परमाणुओं के बीच की दूरी अब सख्ती से बराबर नहीं है $$ , और इस मूल्य के पास उतार चढ़ाव आता है। परमाणुओं के बीच के बंधन में धमनीवाद की संपत्ति होती है: यह एक असममित वसंत की तरह व्यवहार करता है, जो संपीड़ित करने की तुलना में खिंचाव करना आसान होता है। नतीजतन, थर्मल मोशन के दौरान, बॉन्ड को ज्यादातर समय बढ़ाया जाता है, संपीड़ित नहीं किया जाता है, इसलिए औसत दूरी $$ परमाणुओं के बीच से अधिक हो जाता है $$ । बढ़ते तापमान के साथ, यह प्रभाव तेज हो जाता है, परमाणुओं के बीच की दूरी बढ़ जाती है, और सामग्री फैल जाती है।


सामग्रियों के थर्मल विस्तार का कारण: थर्मल गति के दौरान, अंतर-अंतर्क्रियात्मक बलों की धार्मिकता के कारण परमाणुओं के बीच औसत दूरी बढ़ जाती है।

क्या होता है जब सामग्री को संकुचित या बढ़ाया जाता है, जैसा कि चपटा या फैला हुआ गेंदों के मामले में? जब एक सामग्री संकुचित होती है, तो एक बाहरी बल परमाणुओं के बीच की औसत दूरी कम हो जाती है, और जब बढ़ाया जाता है, तो यह बढ़ जाता है।


संपीड़न के तहत, परमाणुओं के बीच संतुलन दूरी कम हो जाती है, जबकि तनाव में यह बढ़ जाता है।

अब हम यह समझने के लिए तैयार हैं कि किसी सामग्री का संपीड़न और तनाव इसकी गर्मी क्षमता को कैसे प्रभावित करता है। कल्पना करें कि हमने सामग्री को निचोड़ लिया, ताकि थर्मल गति के दौरान परमाणुओं के बीच की दूरी अब संतुलन की स्थिति के पास दोलन हो जाए जो बाईं ओर स्थानांतरित हो जाए। इस मामले में, एन्यूरिज्म गायब नहीं हुआ है, इसलिए, पहले की तरह, जब गरम किया जाता है, परमाणुओं के बीच औसत दूरी बढ़ जाएगी। लेकिन एक ही समय में, हम न्यूनतम ऊर्जा की ओर वापस लौटेंगे, जिसका अर्थ है कि सामग्री की ऊर्जा में और कमी आएगी! यह संपीड़न के दौरान सामग्री की गर्मी क्षमता में कमी की व्याख्या करता है: थर्मल विस्तार से इंटरटॉमिक इंटरैक्शन की ऊर्जा में एक छोटी सी अतिरिक्त कमी होती है, इसलिए, सामग्री को गर्म करने के लिए कम ऊर्जा की आवश्यकता होती है।



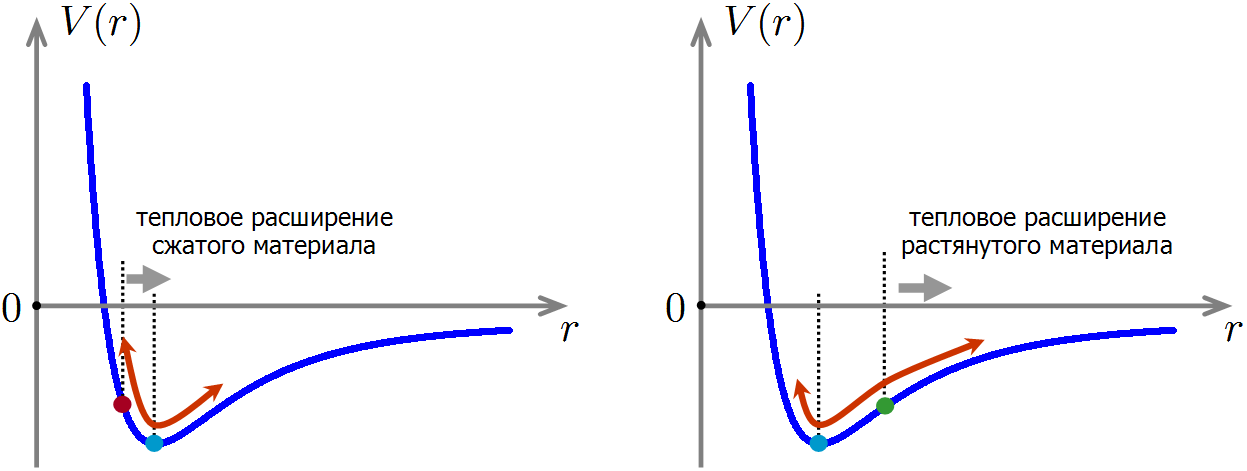
यदि सामग्री को बढ़ाया जाता है, तो स्थिति विपरीत होती है: थर्मल विस्तार के साथ, परमाणुओं की अंतःक्रियात्मक ऊर्जा अस्थिर सामग्री की तुलना में तेजी से बढ़ेगी। इसलिए, एक ही तापमान पर स्ट्रेच की गई सामग्री को गर्म करने के लिए, स्ट्रेचिंग के बिना थोड़ी अधिक ऊर्जा की आवश्यकता होती है, जिसका अर्थ है कि स्ट्रेच की गई सामग्री की गर्मी क्षमता अधिक होगी।

तो, ओलंपियाड समस्या के उदाहरण पर, जो कई दशकों से हल किया गया है (और, शायद, हल किया जाना जारी है) गलती से, हम देखते हैं कि वास्तविक भौतिकी कभी-कभी हमारे अंतर्ज्ञान का विरोध करती है। इसलिए, यह बहुत महत्वपूर्ण है जब समस्याओं को हल करना गणितीय उपकरण का सावधानीपूर्वक उपयोग करना है, न कि सतही तर्क तक सीमित है।

लेख के अनुसार:

गियाकोमो डी पाल्मा, मटिया सी। सोरमानी, एक ठोस क्षेत्र की गर्मी क्षमता पर गुरुत्वाकर्षण का प्रतिदीप्ति प्रभाव: एक प्रसिद्ध समस्या का पुन: परीक्षण, अमेरिकन जर्नल ऑफ फिजिक्स 83, 723 (2015)।
लेख की सार्वजनिक छाप: arxiv.org/pdf/1502.01337