🖖🏾 🔗 📋 एक भाप टरबाइन की रैखिक प्रवाह विशेषता। भाग 2. MATLAB में PT-80 टरबाइन के लिए निर्माण उदाहरण 👈🏾 🤜🏻 👨‍👧

पहले भाग के लिए प्रस्तावना

स्टीम टर्बाइन की मॉडलिंग करना हमारे देश के सैकड़ों लोगों के लिए एक दैनिक कार्य है। शब्द मॉडल के बजाय , यह एक व्यय विशेषता कहने के लिए प्रथागत है। भाप टरबाइनों की खपत विशेषताओं का उपयोग ऐसी समस्याओं को हल करने में किया जाता है जैसे कि बिजली और ताप के लिए समकक्ष ईंधन की विशिष्ट खपत की गणना थर्मल पावर प्लांट द्वारा उत्पादित; सीएचपी का अनुकूलन; थर्मल पावर प्लांट मोड की योजना और रखरखाव।

मैंने भाप टरबाइन की एक नई प्रवाह विशेषता विकसित की है - एक भाप टरबाइन की एक रैखिक प्रवाह विशेषता। विकसित प्रवाह की विशेषता इन समस्याओं को हल करने में सुविधाजनक और प्रभावी है। हालांकि, फिलहाल इसे केवल दो वैज्ञानिक पत्रों में वर्णित किया गया है:

और अब अपने ब्लॉग में मैं यह चाहूंगा:

सबसे पहले, नई प्रवाह दर विशेषता के बारे में बुनियादी सवालों के जवाब देने के लिए एक सरल और सुलभ भाषा में (देखें। एक भाप टरबाइन की रैखिक प्रवाह दर विशेषता। भाग 1. बुनियादी प्रश्न );
दूसरे, एक नई प्रवाह विशेषता के निर्माण का एक उदाहरण प्रदान करें जो निर्माण विधि और विशेषता के गुणों (नीचे देखें) दोनों को समझने में मदद करेगा;
तीसरा, स्टीम टरबाइन के संचालन मोड के बारे में दो प्रसिद्ध कथनों का खंडन करना (देखें। स्टीम टर्बाइन की रैखिक प्रवाह विशेषताओं। भाग 3. भाप टरबाइन के संचालन के बारे में मिथकों को दूर करना )।

1. स्रोत डेटा

एक रैखिक प्रवाह विशेषता के निर्माण के लिए प्रारंभिक डेटा हो सकता है

वास्तविक शक्ति मान क्यू ₀ , एन, क्यू _पी , क्यू _टी भाप टरबाइन के संचालन के दौरान मापा जाता है,
मानक और तकनीकी दस्तावेज से नामोग्राम q _टी सकल।

बेशक, क्यू ₀ , एन, क्यू _पी , क्यू _टी के वास्तविक तात्कालिक मान आदर्श स्रोत डेटा हैं। इस तरह के डेटा को इकट्ठा करने में समय लगता है।

ऐसे मामलों में जहां क्यू ₀ , एन, क्यू _पी , क्यू _टी के वास्तविक मूल्य उपलब्ध नहीं हैं, आप नॉमोग्राम क्यू _टी सकल प्रक्रिया कर सकते हैं। वे, बदले में, माप के आधार पर प्राप्त किए गए थे। VM Gornstein में टरबाइन परीक्षणों के बारे में अधिक पढ़ें और ऊर्जा प्रणालियों के तरीकों के अनुकूलन के अन्य तरीके ।

2. एक रैखिक प्रवाह विशेषताओं के निर्माण के लिए एल्गोरिथ्म

निर्माण एल्गोरिथ्म में तीन चरण होते हैं।

नाममात्र या माप के अनुवाद से सारणीबद्ध दृश्य निकलता है।
एक भाप टरबाइन की प्रवाह विशेषता का रैखिककरण।
भाप टरबाइन की नियंत्रण सीमा की सीमाओं का निर्धारण।

जब नॉमोग्राम क्यू _टी सकल के साथ काम करते हैं, तो पहला कदम त्वरित होता है। इस कार्य को डिजिटलीकरण कहा जाता है । मौजूदा उदाहरण के लिए 9 नामांकनों को डिजिटाइज़ करने में मुझे लगभग 40 मिनट लगे।

दूसरे और तीसरे चरण में गणितीय पैकेज के उपयोग की आवश्यकता होती है। मैं कई वर्षों से MATLAB से प्यार करता हूं और उसका उपयोग करता हूं। एक रैखिक प्रवाह विशेषता के निर्माण का मेरा उदाहरण इसमें बनाया गया है। एक उदाहरण लिंक से डाउनलोड किया जा सकता है, रन और स्वतंत्र रूप से एक रैखिक प्रवाह विशेषता के निर्माण की विधि का पता लगा सकता है।

प्रश्न में टरबाइन के लिए प्रवाह की विशेषता मोड मापदंडों के निम्नलिखित निश्चित मूल्यों के लिए बनाई गई थी:

एकल-चरण संचालन
मध्यम दबाव भाप दबाव = 13 kgf / cm2,
कम दबाव भाप का दबाव = 1 kgf / cm2।

चुचुएवा-पीटी -80-लीनियर-विशेषता-कर्व.रार संग्रह की सामग्री ।

1) बिजली उत्पादन के लिए विशिष्ट खपत क्यूटी सकल के नामांकित (चिह्नित लाल डॉट्स डिजीटल हैं - तालिका में स्थानांतरित):

PT80_qt_Qm_eq_0_digit.png,
PT80_qt_Qm_eq_100_digit.png,
PT80_qt_Qm_eq_120_digit.png,
PT80_qt_Qm_eq_140_digit.png,
PT80_qt_Qm_eq_150_digit.png,
PT80_qt_Qm_eq_20_digit.png,
PT80_qt_Qm_eq_40_digit.png,
PT80_qt_Qm_eq_60_digit.png,
PT80_qt_Qm_eq_80_digit.png।

2) डिजिटलीकरण का परिणाम (प्रत्येक सीएसवी फ़ाइल एक पीएनजी फ़ाइल से मेल खाती है):

पीटी 80_Qm_eq_0.csv,
पीटी 80_Qm_eq_100.csv,
पीटी 80_Qm_eq_120.csv,
पीटी 80_Qm_eq_140.csv,
पीटी 80_Qm_eq_150.csv,
पीटी 80_Qm_eq_20.csv,
पीटी 80_Qm_eq_40.csv,
पीटी 80_Qm_eq_60.csv,
पीटी 80_Qm_eq_80.csv।

3) गणना और रेखांकन के साथ MATLAB स्क्रिप्ट :

PT_80_linear_characteristic_curve.m

4) नामांकितों के डिजिटलीकरण और सारणीबद्ध रूप में एक रैखिक प्रवाह विशेषता के निर्माण का परिणाम :

PT_80_linear_characteristic_curve.xlsx।

चरण 1. नाममात्र या माप के अनुवाद एक सारणीबद्ध दृश्य में परिणाम

1. सोर्स डाटा प्रोसेसिंग

हमारे उदाहरण के लिए प्रारंभिक डेटा नॉमोग्राम क्यू _टी सकल हैं।

कई नाममात्र को डिजिटाइज़ करने के लिए, आपको एक विशेष उपकरण की आवश्यकता होती है। मैंने इन उद्देश्यों के लिए बार-बार एक वेब एप्लिकेशन का उपयोग किया है। आवेदन सरल, सुविधाजनक है, लेकिन प्रक्रिया को स्वचालित करने के लिए पर्याप्त लचीलापन नहीं है। काम का हिस्सा मैन्युअल रूप से किया जाना है।

इस चरण में, नाममात्र के चरम बिंदुओं को डिजिटाइज़ करना महत्वपूर्ण है जो स्टीम टरबाइन के समायोजन रेंज की सीमाओं को परिभाषित करते हैं ।

काम एप्लिकेशन का उपयोग करके प्रत्येक पीएनजी फ़ाइल में डिस्चार्ज विशेषता के बिंदुओं को चिह्नित करना था, परिणामस्वरूप सीएसवी डाउनलोड करें और एक तालिका में सभी डेटा एकत्र करें। डिजिटलीकरण का परिणाम पीटी -80-रैखिक-विशेषता-कर्व.xlsx, शीट "पीटी -80", तालिका "इनपुट डेटा" फ़ाइल में पाया जा सकता है।

2. बिजली की इकाइयों के लिए माप की इकाइयों को लाना

अगला, शीट "पीटी -80" पर हम सूत्र के अनुसार क्यू ₀ के मूल्यों की गणना करते हैं

$ $ प्रदर्शन $ $ \ शुरू {समीकरण} Q_0 = \ frac {q_T \ cdot N} {1000} + Q_P + Q_T \ qquad (1) \ अंत {समीकरण} $ $ प्रदर्शन $ $

और हम सभी प्रारंभिक मूल्यों को MW में लाते हैं। गणना एमएस एक्सेल का उपयोग करके कार्यान्वित की जाती है।

परिणामी तालिका "इनपुट डेटा (यूनिट पावर)" एल्गोरिथ्म के पहले चरण का परिणाम है।

चरण 2. स्टीम टरबाइन प्रवाह विशेषता का रैखिककरण

1. परीक्षण MATLAB

इस चरण में, आपको MATLAB संस्करण को 7.3 से कम स्थापित करने और खोलने की आवश्यकता है (यह एक पुराना संस्करण है, वर्तमान 8.0)। MATLAB में PT_80_linear_characteristic_curve.m फ़ाइल खोलें, इसे चलाएं और सुनिश्चित करें कि यह काम कर रहा है। सब कुछ सही ढंग से काम करता है, यदि कमांड लाइन पर स्क्रिप्ट चलाने के परिणामों पर आपको निम्न संदेश दिखाई देता है:

    PT_80_linear_characteristic_curve.xlsx  1  : a(N) = 2.317, a(Q) = 0.621, a(Q) = 0.255, a0 = 33.874   = 0.006, (0.57%)      = 37

यदि आपके पास कोई त्रुटि है, तो अपने आप को पता लगाएं कि उन्हें कैसे ठीक किया जाए।

2. गणना

सभी गणना फ़ाइल PT_80_linear_characteristic_curve.m में लागू की जाती हैं। आइए इसे भागों में विचार करें।

1) हम पिछले चरण में प्राप्त स्रोत फ़ाइल, पत्रक, तालिका "स्रोत डेटा (क्षमता की इकाई)" से युक्त कोशिकाओं की श्रेणी का नाम दर्शाते हैं।

 XLSFileName = 'PT_80_linear_characteristic_curve.xlsx'; XLSSheetName = 'PT-80'; XLSRange = 'F3:I334';

2) हम MATLAB में स्रोत डेटा पढ़ते हैं।

 sourceData = xlsread(XLSFileName, XLSSheetName, XLSRange); N = sourceData(:,1); Qm = sourceData(:,2); Ql = sourceData(:,3); Q0 = sourceData(:,4); fprintf('    %s  %1.0f \n', XLSFileName, toc);

हम स्टीम क्यू _पी की औसत प्रवाह दर के लिए चर क्यूएम का उपयोग करते हैं, मध्य से सूचकांक एम औसत है; इसी तरह, हम कम दबाव वाले स्टीम फ्लो Q _{n के} लिए वैरिएबल Ql का उपयोग करते हैं, कम से सूचकांक l कम है।

3) गुणांकों को परिभाषित करें α _i ।

प्रवाह विशेषताओं के लिए सामान्य सूत्र को याद करें

$$ प्रदर्शन $$ \ start {समीकरण} Q_0 = f (N, Q_, Q_) \ qquad (2) \ end {समीकरण} $ $ प्रदर्शन $ $

और स्वतंत्र (x_digit) और आश्रित (y_digit) चर निर्दिष्ट करें।

 x_digit = [N Qm Ql ones(size(N,1),1)]; %  N,   Q,   Q,   y_digit = Q0; %    Q0

यदि आप यह नहीं समझते हैं कि x_digit मैट्रिक्स में एकल वेक्टर (अंतिम कॉलम) क्यों है, तो रैखिक प्रतिगमन सामग्री पढ़ें। प्रतिगमन विश्लेषण के विषय पर, मैं ड्रेपर एन, स्मिथ एच। एप्लाइड प्रतिगमन विश्लेषण पुस्तक की सिफारिश करता हूं। न्यूयॉर्क: विली, प्रेस में, 1981. 693 पी। (रूसी में उपलब्ध)।

भाप टरबाइन के रैखिक प्रवाह की विशेषता का समीकरण

$$ प्रदर्शन $ $ \ _ {समीकरण} शुरू करें Q_0 = \ Alpha_N \ cdot N + \ Alpha_T \ cdot Q_P + \ Alpha_T \ cdot Q_T + \ Alpha_0 \ qquad (3) \ end {समीकरण {$ $ $ $

एक बहु रैखिक प्रतिगमन मॉडल है। गुणांक α _मैं "सभ्यता के महान लाभ" का उपयोग करके निर्धारित किया जाएगा - कम से कम वर्गों की विधि। अलग-अलग, मैं ध्यान देता हूं कि 1795 में गॉस द्वारा सबसे कम वर्ग विधि विकसित की गई थी।

MATLAB में, यह एक पंक्ति में किया जाता है।

 A = regress(y_digit, x_digit); fprintf(': a(N) = %4.3f, a(Q) = %4.3f, a(Q) = %4.3f, a0 = %4.3f\n',... A);

परिवर्तनीय ए में वांछित गुणांक शामिल हैं (MATLAB कमांड लाइन पर संदेश देखें)।

इस प्रकार, पीटी -80 स्टीम टरबाइन के प्राप्त रैखिक प्रवाह की विशेषता का रूप है

$$ प्रदर्शन $ $ \ _ {समीकरण} प्रारंभ_ Q_0 = 2.317 \ cdot N + 0.621 \ cdot Q_ + 0.255 \ cdot Q_ + 33.874 \ qquad (4) \ अंत {समीकरण} $ $ प्रदर्शन $ $

4) हम प्राप्त प्रवाह विशेषता के रैखिककरण की त्रुटि का अनुमान लगाते हैं।

 y_model = x_digit * A; err = abs(y_model - y_digit) ./ y_digit; fprintf('  = %1.3f, (%4.2f%%)\n\n', mean(err), mean(err)*100);

रैखिककरण त्रुटि 0.57% है (MATLAB कमांड लाइन पर संदेश देखें)।

भाप टरबाइन के रैखिक प्रवाह की विशेषता का उपयोग करने की सुविधा का आकलन करने के लिए, हम ज्ञात भार मूल्यों N, Q _p , Q _{t पर} उच्च दबाव भाप प्रवाह दर Q ₀ की गणना करने की समस्या को हल करते हैं।

चलो N = 82.3 MW, Q _p = 55.5 MW, Q _t = 62.4 MW, तब

$ $ प्रदर्शन $ $ \ शुरू {समीकरण} Q_0 = 2.317 \ cdot 82.3 + 0.621 \ cdot 55.5 + 0.255 \ cdot 62.4 + 33.874 = 274.9 \ qquad (5) \ अंत (समीकरण) $ $ $ $ प्रदर्शित करें

आपको याद दिला दूं कि औसत गणना त्रुटि 0.57% है।

आइए हम इस सवाल पर लौटते हैं कि विद्युत उत्पादन के लिए विशिष्ट खपत q _टी सकल के नाममात्र की तुलना में मौलिक रूप से भाप टरबाइन की रैखिककृत विशेषता क्यों अधिक सुविधाजनक है? अभ्यास में मूलभूत अंतर को समझने के लिए, दो समस्याओं को हल करें।

क्यू _{0 की} गणना प्रत्याहारों और आपकी आंखों का उपयोग करके संकेतित सटीकता के साथ करें।
नामांकनों का उपयोग करके Q ₀ की गणना करने की प्रक्रिया को स्वचालित करें।

जाहिर है, पहले कार्य में, आंख द्वारा q सकल मूल्यों का निर्धारण, सकल त्रुटियों से भरा हुआ है।

दूसरा कार्य स्वचालित करने के लिए बोझिल है। चूँकि q q मान स्थूल रूप से अशुभ होते हैं , ऐसे स्वचालन के लिए डिजिटाइज्ड बिंदुओं की संख्या वर्तमान उदाहरण की तुलना में दस गुना बड़ी होती है। अकेले डिजिटलीकरण पर्याप्त नहीं है, गैर-रैखिक सकल मूल्यों के इंटरपोलिंग (अंकों के बीच मूल्यों को खोजने) के लिए एक एल्गोरिथ्म को लागू करना भी आवश्यक है।

चरण 3. भाप टरबाइन के समायोजन रेंज की सीमाओं का निर्धारण

1. गणना

समायोजन रेंज की गणना करने के लिए, हम एक और "सभ्यता का अच्छा" का उपयोग करेंगे - उत्तल पतवार विधि, उत्तल पतवार।

MATLAB में, यह निम्नानुसार किया जाता है।

 indexCH = convhull(N, Qm, Ql, 'simplify', true); index = unique(indexCH); regRange = [N(index) Qm(index) Ql(index)]; regRangeQ0 = [regRange ones(size(regRange,1),1)] * A; fprintf('     = %d\n\n', size(index,1));

कनवल्ल () विधि चर N, Qm, Ql के मानों द्वारा दी गई समायोजन सीमा के सीमा बिंदुओं को निर्धारित करती है। परिवर्तनशील अनुक्रमणिका में Delaunay triangulation का उपयोग करके निर्मित त्रिभुजों के कोने होते हैं। RegRange चर में समायोजन रेंज के सीमा बिंदु शामिल हैं; चर regRangeQ0 - नियंत्रण सीमा के सीमा बिंदुओं के लिए उच्च दबाव भाप प्रवाह दर।

गणना परिणाम PT_80_linear_characteristic_curve.xlsx फ़ाइल में पाया जा सकता है, शीट "PT-80-परिणाम", तालिका "समायोजन सीमाएँ"।

रैखिक प्रवाह विशेषता निर्मित। यह एक सूत्र (4) और 37 बिंदु हैं जो संबंधित तालिका में समायोजन रेंज की सीमाओं (शेल) को परिभाषित करते हैं।

2. सत्यापन

गणना प्रक्रियाओं को स्वचालित करते समय, क्यू ₀ यह जांचना आवश्यक है कि क्या एन, क्यू _पी , क्यू _टी के मूल्यों के साथ कुछ बिंदु समायोजन सीमा के अंदर है या इसके बाहर है (मोड तकनीकी रूप से संभव नहीं है)। MATLAB में, यह निम्नानुसार किया जा सकता है।

हम एन, क्यू _पी , क्यू _टी के मान सेट करते हैं जिन्हें हम जांचना चाहते हैं।

 n = 75; qm = 120; ql = 50;

हम जांच करते हैं।

 in1 = inpolygon(n, qm, regRange(:,1),regRange(:,2)); in2 = inpolygon(qm, ql, regRange(:,2),regRange(:,3)); in = in1 && in2; if in fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f     \n', n, qm, ql); else fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f      ( )\n', n, qm, ql); end

सत्यापन दो चरणों में किया जाता है:

चर in1 इंगित करता है कि क्या N, Q _p के मान अक्ष N, Q _p पर शेल के प्रक्षेपण में गिर गए हैं;
इसी तरह, चर in2 से पता चलता है कि क्या Q _p , Q _t , Q _p , Q _t के अक्ष पर शेल के प्रक्षेपण के अंदर _है ।

यदि दोनों चर 1 (सत्य) के बराबर हैं, तो वांछित बिंदु शेल के अंदर है, जो भाप टरबाइन की समायोजन सीमा निर्धारित करता है।

एक भाप टरबाइन की प्राप्त रेखीय प्रवाह विशेषता का चित्रण

सभ्यता के सबसे "उदार लाभ" हमें गणना के परिणामों को दर्शाने के रूप में मिले।

पहले हमें यह कहने की आवश्यकता है कि जिस स्थान पर हम ग्राफ बनाते हैं, अर्थात्, एक्सिस के साथ अंतरिक्ष - एन, वाई - क्यू _टी , जेड - क्यू ₀ , डब्ल्यू - क्यू _पी , को शासन स्थान कहा जाता है (परिस्थितियों में थर्मल पावर प्लांट के संचालन का अनुकूलन देखें) रूस के बिजली और क्षमता का थोक बाजार

)। इस स्थान का प्रत्येक बिंदु एक भाप टरबाइन के संचालन के एक निश्चित मोड को परिभाषित करता है। मोड हो सकता है

तकनीकी रूप से व्यवहार्य, यदि बिंदु शेल के अंदर है जो समायोजन रेंज को परिभाषित करता है,
तकनीकी रूप से संभव नहीं है यदि बिंदु इस शेल के बाहर है।

अगर हम स्टीम टर्बाइन (Q _p = 0, Q _t = 0) के संक्षेपण मोड के बारे में बात करते हैं, तो रैखिक प्रवाह विशेषता एक सीधी रेखा खंड है । यदि हम एक टी-टाइप टरबाइन के बारे में बात करते हैं, तो अक्षीय प्रवाह विशेषता अक्षीय x - N, y - Q _t , z - Q _{0 के} साथ त्रि-आयामी शासन स्थान में एक फ्लैट बहुभुज है , जो कल्पना करना आसान है। पीटी-प्रकार के टरबाइन के लिए, विज़ुअलाइज़ेशन सबसे मुश्किल है, क्योंकि इस तरह के टरबाइन के रैखिक प्रवाह की विशेषता चार-आयामी अंतरिक्ष में एक फ्लैट बहुभुज है (स्पष्टीकरण और उदाहरणों के लिए, रूस के थोक बिजली और बिजली बाजार में एक थर्मल पावर प्लांट के संचालन का अनुकूलन देखें, एक टरबाइन प्रवाह विशेषता का अनुभाग रैखिककरण )।

1. एक भाप टरबाइन की प्राप्त रैखिक प्रवाह विशेषताओं का चित्रण

चलो शासन स्थान में तालिका "इनपुट डेटा (पावर की इकाई)" के मूल्यों का निर्माण करते हैं।

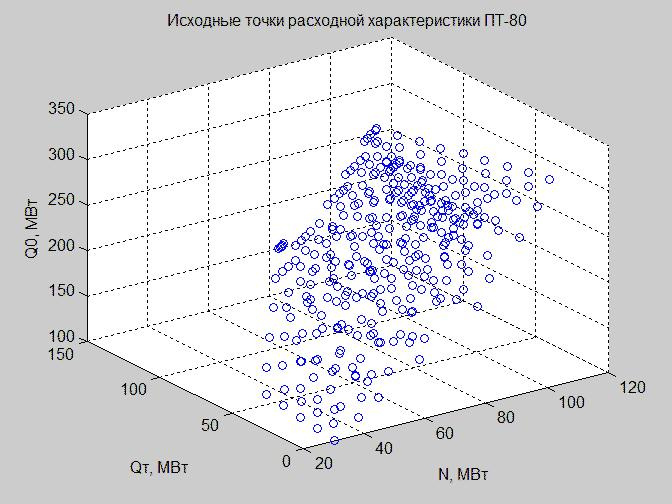
अंजीर। 3. एक्सिस के साथ शासन स्थान में प्रवाह विशेषताओं के शुरुआती बिंदु एक्स - एन, वाई - क्यू _टी , जेड - क्यू ₀

चूँकि हम चार-आयामी अंतरिक्ष में निर्भरता का निर्माण नहीं कर सकते हैं, इसलिए हम अभी तक सभ्यता की इतनी अच्छी स्थिति तक नहीं पहुंचे हैं, हम क्यू _एन के मूल्यों पर निम्नानुसार काम करते हैं: उन्हें (छवि 3), फिक्स (छवि 4) को बाहर करें (MATLAB में ग्राफ़ के निर्माण के लिए कोड देखें)।

हम क्यू _पी = 40 मेगावाट के मूल्य को ठीक करते हैं और शुरुआती बिंदु और रैखिक प्रवाह विशेषता का निर्माण करते हैं।

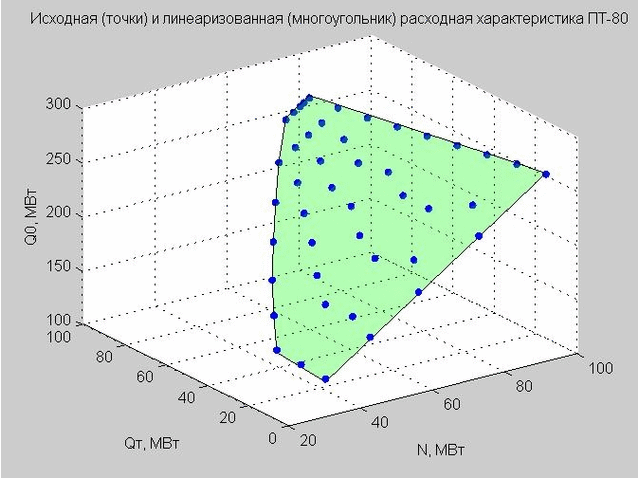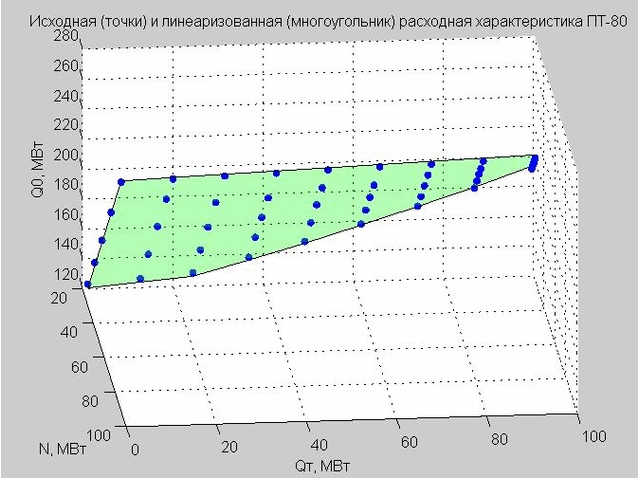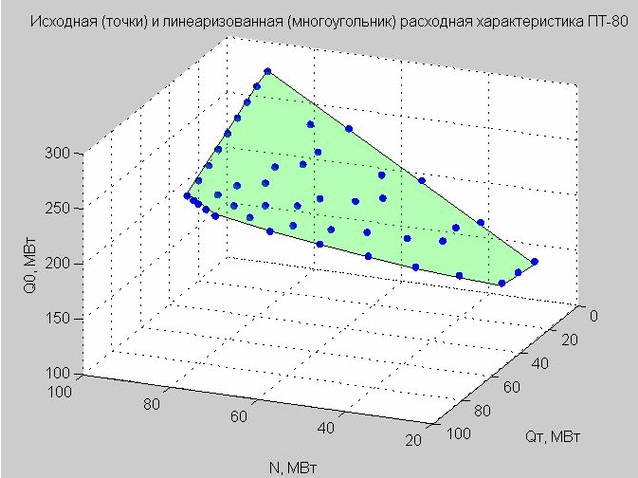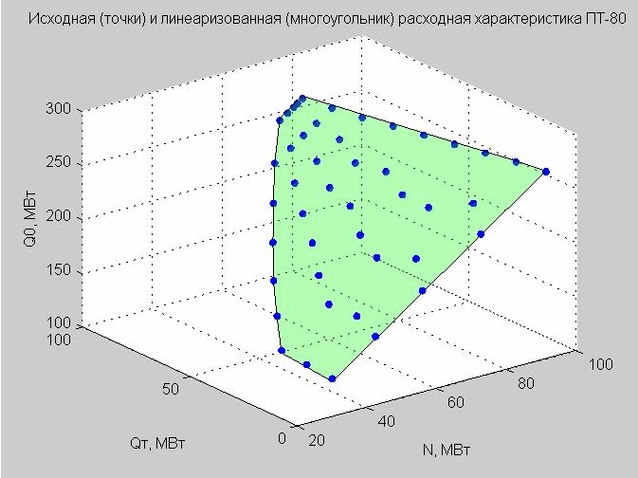
अंजीर। 4. डिस्चार्ज पॉइंट्स (नीले डॉट्स) के शुरुआती बिंदु, रैखिककृत डिस्चार्ज विशेषता (ग्रीन फ्लैट बहुभुज)

हमें रैखिक प्रवाह दर विशेषता (4) के सूत्र पर लौटें जो हमने प्राप्त की थी। अगर हम Q _p = 40 MW MW तय करते हैं, तो फॉर्मूला होगा

$ $ प्रदर्शन $ $ \ शुरू {समीकरण} Q_0 = 2.317 \ cdot N + 0.255 \ cdot Q_T + 58.714 \ qquad (6) \ अंत {समीकरण} $ $ प्रदर्शन $ $

यह मॉडल एक्स-एन, वाई - क्यू _टी , जेड - क्यू _{0 के} साथ तीन आयामी अंतरिक्ष में एक फ्लैट बहुभुज को एक टी-टाइप टरबाइन के साथ सादृश्य द्वारा परिभाषित करता है (हम इसे छवि 4 में देखते हैं)।

कई साल पहले, जब क्यू सकल नाम विकसित किए गए थे, प्रारंभिक डेटा के विश्लेषण के चरण में एक मूलभूत त्रुटि हुई थी। कम से कम वर्गों की विधि लागू करने और एक अज्ञात कारण के लिए भाप टरबाइन की एक रैखिक प्रवाह विशेषता का निर्माण करने के बजाय, उन्होंने एक आदिम गणना की:

$$ प्रदर्शन $$ \ start {समीकरण} Q_0 (N) = Q_ Q = Q_0 - Q_ - Q_ \ qquad (7) \ end {समीकरण} $ $ प्रदर्शन $ $

उच्च दाब भाप Q _{0 के} प्रवाह दर से घटाकर vapors Q _t , Q _p _की प्रवाह दर और परिणामी अंतर Q ₀ (N) = Q _e को विद्युत उत्पादन के लिए जिम्मेदार ठहराया। प्राप्त मान Q ₀ (N) = Q _{e को} N से विभाजित किया _{गया था} और kcal / kW · h में परिवर्तित किया गया _था , जिससे एक विशिष्ट उपभोग q _t सकल प्राप्त हुआ। यह गणना ऊष्मप्रवैगिकी के नियमों का पालन नहीं करती है।

प्रिय पाठकों, शायद आप अज्ञात कारण जानते हैं? इसे साझा करें!

2. भाप टरबाइन के समायोजन रेंज का चित्रण

चलो शासन स्थान में समायोजन रेंज का खोल देखते हैं। इसके निर्माण के शुरुआती बिंदु अंजीर में प्रस्तुत किए गए हैं। 5. ये वही बिंदु हैं जो हम अंजीर में देखते हैं। 3, हालांकि, पैरामीटर Q _{0 को} अब बाहर रखा गया है।

अंजीर। 5. एक्सिस के साथ शासन स्थान में प्रवाह विशेषताओं के शुरुआती बिंदु एक्स - एन, वाई - क्यू _पी , जेड - क्यू _टी

अंजीर में कई बिंदु। 5 उत्तल है। उत्तल () फ़ंक्शन का उपयोग करते हुए, हमने उन बिंदुओं को परिभाषित किया जो इस सेट के बाहरी शेल को परिभाषित करते हैं।

Delaunay त्रिकोण (जुड़े त्रिकोण का एक सेट) हमें समायोजन रेंज के खोल का निर्माण करने की अनुमति देता है। त्रिकोण के कोने विचाराधीन PT-80 भाप टरबाइन के समायोजन रेंज के सीमा मूल्य हैं।

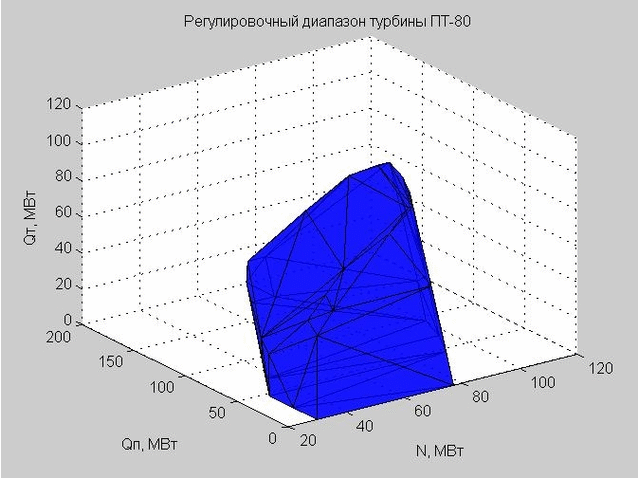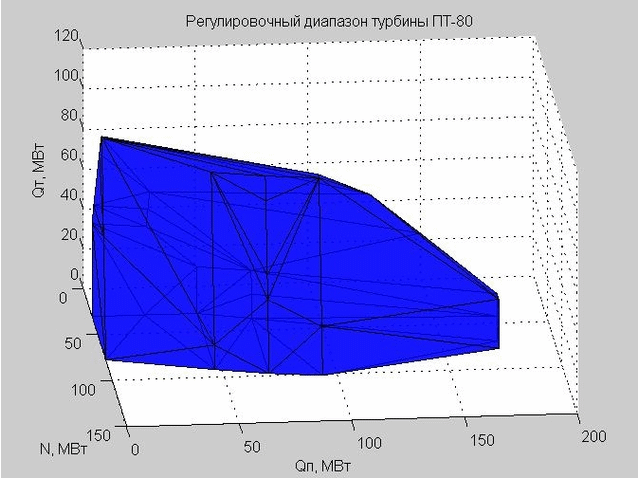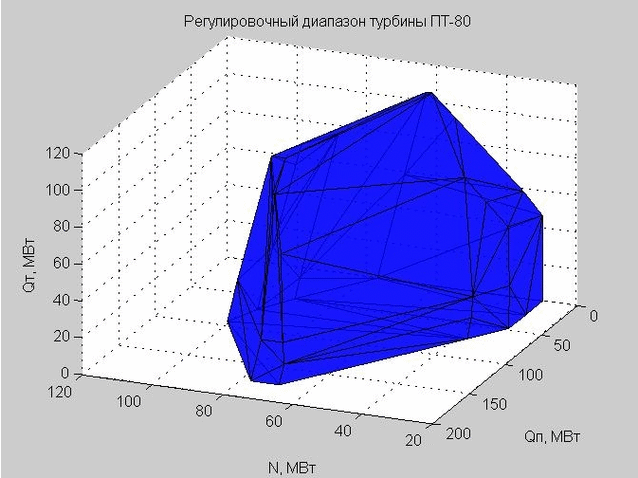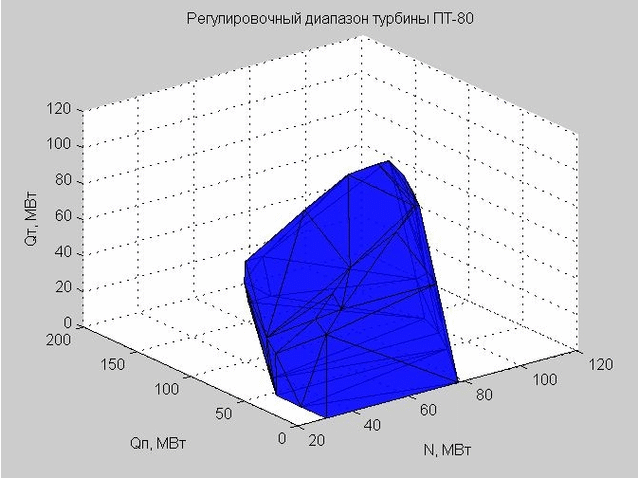
अंजीर। 6. समायोजन रेंज का खोल, कई त्रिकोणों द्वारा दर्शाया गया

जब हमने समायोजन सीमा के अंदर पहुंचने के लिए एक निश्चित बिंदु पर एक जाँच की, तो हमने जाँच की कि क्या यह बिंदु परिणामी शेल के अंदर या बाहर स्थित है।

ऊपर प्रस्तुत सभी ग्राफ़ MATLAB टूल (PT_80_linear_characteristic_curve.m देखें) का उपयोग करके बनाए गए हैं।

एक रैखिक टरबाइन के संचालन के विश्लेषण से संबंधित कार्यों को एक रैखिक प्रवाह विशेषता का उपयोग करते हुए

यदि आप एक डिप्लोमा या शोध प्रबंध कर रहे हैं, तो मैं आपको कई कार्यों की पेशकश कर सकता हूं, जिनमें से वैज्ञानिक नवीनता आप पूरी दुनिया के लिए आसानी से साबित कर सकते हैं। इसके अलावा, आप एक उत्कृष्ट और उपयोगी काम करेंगे।

टास्क 1

दिखाओ कि जब कम दबाव वाष्प दबाव Q _t बदल जाता है तो फ्लैट बहुभुज कैसे बदलता है।

टास्क २

दिखाएँ कि कैसे फ्लैट बहुभुज बदलता है जब कंडेनसर में दबाव बदलता है।

टास्क 3

जाँच करें कि क्या रैखिक प्रवाह की विशेषता वाले गुणांक को शासन के अतिरिक्त मापदंडों के कार्यों के रूप में दर्शाया जा सकता है:

$$ प्रदर्शन $ $ \ _ {समीकरण} \ अल्फा_ = एफ (पी_ {0}, ...); \\ \ Alpha_P = f (p_ {P}, ...); \\ \ Alpha_T = f (p_ {T}, ...); \\ \ Alpha_0 = f (p_ {2}, ...)। \ अंत {समीकरण} $ $ प्रदर्शन $ $

यहाँ पी ₀ - उच्च दबाव भाप दबाव, पी _पी - मध्यम दबाव भाप दबाव, पी _टी - कम दबाव भाप दबाव, पी ₂ - कंडेनसर में निकास भाप दबाव, सभी इकाइयां kgf / cm2 हैं।

परिणाम को उचित ठहराएं।

संदर्भ

चुचुएवा I.A., इंकिना एन.ई. सीएचपी का अनुकूलन इलेक्ट्रिक पावर और रूस की क्षमता के थोक बाजार की स्थितियों में // विज्ञान और शिक्षा: एमएसटीयू का वैज्ञानिक संस्करण। NE बाऊमन। 2015. नंबर 8. एस 195-238।

चुचुवे आई। ए। संयुक्त पीढ़ी // विज्ञान और शिक्षा के मोड में विद्युत और तापीय ऊर्जा की आपूर्ति के लिए थर्मल पावर प्लांट के समकक्ष ईंधन की विशिष्ट खपत का निर्धारण करने के लिए कम्प्यूटेशनल विधियाँ: MSTU का वैज्ञानिक प्रकाशन। NE बाऊमन। 2016. नंबर 2. पी। 135-165।

एक भाप टरबाइन की रैखिक प्रवाह विशेषता।

भाग 1. प्रमुख मुद्दे
भाग 2. MATLAB में PT-80 टरबाइन के लिए निर्माण उदाहरण
भाग 3. भाप टरबाइन ऑपरेटिंग मोड के बारे में मिथकों को दूर करना

एक भाप टरबाइन की रैखिक प्रवाह विशेषता। भाग 2. MATLAB में PT-80 टरबाइन के लिए निर्माण उदाहरण