हम कण भौतिकी को समझते हैं: 3) तरंगें, शास्त्रीय रूप

1. एक वसंत पर गेंद, न्यूटोनियन संस्करण
2. एक वसंत पर एक क्वांटम गेंद
3. लहरें, क्लासिक लुक
4. लहरें, गति का शास्त्रीय समीकरण
5. क्वांटम तरंगें
6. फील्ड्स
7. कण क्वांटा हैं
8. कण खेतों के साथ कैसे संपर्क करते हैं

दोलनों के समीकरणों से निपटने के बाद - लगभग हर चीज का वर्णन करता है जो कूदता है, कंपन करता है, आगे और पीछे लुढ़कता है, जैसे वसंत पर एक गेंद - हम समान रूप से सामान्य प्राकृतिक घटना, तरंगों पर आगे बढ़ सकते हैं। लहरें हर जगह हैं: ध्वनि और प्रकाश, भूकंप, तालाब की सतह पर लहरें आदि।


अंजीर। 1

लेकिन इससे पहले, मैं आपको चेतावनी देता हूं कि "लहर" शब्द भ्रामक हो सकता है, क्योंकि भौतिकी में इसका मतलब अंग्रेजी में नहीं है। भौतिकी में, इसका मतलब यह नहीं है कि हम आमतौर पर समुद्र के किनारे पर एक लहर कहते हैं - एक शिखा और एक खोखला। भौतिकी में, तरंगें तरंगों का एक क्रम है, कई लकीरें और गर्तें जो एक ही दिशा में एक साथ चलती हैं। सबसे सरल रूप की एक लहर में, सभी लकीरें एक ही ऊंचाई की होती हैं और एक दूसरे से एक दूरी पर होती हैं। हम इस तरह के एक मामले पर विचार करेंगे।

लहरें एक उत्कृष्ट घटना हैं, अगर आप इसके बारे में सोचते हैं। कल्पना कीजिए कि आपने और आपके दोस्त ने एक लंबी रस्सी ली और उसे कमरे में कसकर खींच लिया (चित्र -2)। फिर कल्पना करें कि आपके दोस्त ने रस्सी (हरा) के एक छोर के साथ कई बार ऊपर और नीचे चैट किया। रस्सी के अंत में एक लहर दिखाई देगी और यह कमरे के माध्यम से आपके रस्सी (लाल) के अंत तक जाएगी।


अंजीर। 2

यह आश्चर्यजनक है। मेरा मतलब है - यह हमारे ब्रह्मांड की हर चीज के लिए वास्तव में आश्चर्यजनक, मजबूत और महत्वपूर्ण है, जिसमें आप व्यक्तिगत रूप से शामिल हैं। देखो क्या हुआ। कोई भी भौतिक वस्तु बाईं से दाईं ओर नहीं चली गई - इससे पहले कि आपका दोस्त रस्सी के अंत को स्थानांतरित करना शुरू करे, उसे पूरे कमरे में फैला दिया गया था, और अंत में, रस्सी खत्म होने के बाद आपका हिलना बंद हो जाता है और लहर गायब हो जाती है, रस्सी पूरी तरह से खिंचती रहेगी कमरा, जैसा भी था। और फिर भी! ऊर्जा और सूचना कमरे में घूम गई। जिस तरह से लहर आपके दोस्त द्वारा रस्सी के कंपन पर खर्च की गई ऊर्जा को स्थानांतरित करती है - और इसके रूप में जानकारी लेती है कि उसने कितनी बार और कितनी जल्दी इसे खींचा है - आपके लिए, जहां यह आपके हाथ को हिला देता है। और इस मामले में, वह भी कई बार और उसी क्रम में आपके हाथ हिलाएगा। वाह! एक भी भौतिक वस्तु कमरे से नहीं गुजरी, और ऊर्जा और सूचना चली गई।

या प्रतीक्षा करें। लेकिन क्या हमें लहर को एक भौतिक वस्तु नहीं मानना ​​चाहिए? रस्सी के रूप में ही शारीरिक?

इस गहन प्रश्न को याद करते हुए, हम लहर की उपस्थिति और व्यवहार का वर्णन करने के लिए आवश्यक गणितीय सूत्रों की एक छोटी संख्या की ओर मुड़ते हैं, और फिर समीकरणों को लिखने के लिए थोड़ा और गणित का उपयोग करते हैं जिनके समाधान तरंग हैं। यह वही है जो हमने एक क्लासिक स्प्रिंग बॉल के लिए किया था।

एक निश्चित समय पर एक अनंत तरंग के लिए सूत्र

वसंत पर गेंद के तुरंत बाद लेखों की यह श्रृंखला लहरों पर जाती है क्योंकि लहर एक तरह का डबल ऑसिलेटर है। यह समय और अंतरिक्ष दोनों में उतार-चढ़ाव करता है। हम अक्षर "t" और "x" के साथ स्थान के साथ समय नामित करेंगे।

अंजीर पर ध्यान दें। 3. यह एक बड़ी दूरी पर दोनों दिशाओं में फैली एक लहर को दर्शाता है, जिस पर कई लकीरें और अवसाद फिट होते हैं। यह अंजीर में लहर से अलग है। 2, जिसमें केवल कुछ लकीरें और अवसाद हैं। लेकिन यह अंतर अप्रासंगिक है - अंजीर में। 2 मुझे यह बताने की जरूरत है कि सटीक तरंग के लिए क्या मायने नहीं रखता था; अब हम तरंगों के लिए गणितीय सूत्र पर ध्यान केंद्रित करेंगे, और यह करना बहुत आसान है कि क्या लहर में बड़ी संख्या में लकीरें और समान आकार के अवसाद हैं। साथ ही, यह मामला यह समझने के लिए बहुत उपयोगी साबित होगा कि क्वांटम यांत्रिकी तरंगों के व्यवहार को कैसे प्रभावित करता है।



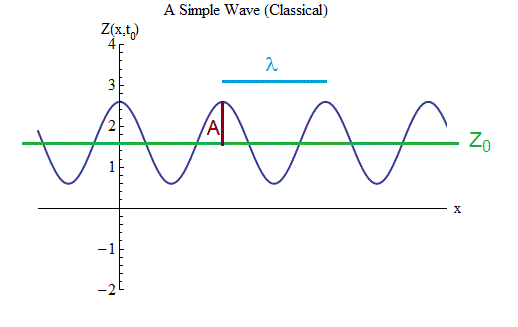
अंजीर। 3

सबसे पहले, हमें संकेतन को निर्धारित करने और अंजीर में गति और तरंग का वर्णन करने वाले एक सूत्र को लिखने की आवश्यकता है। 3, जैसा कि हमने वसंत पर गेंद के लिए किया था।

ग्राफ एक निश्चित समय अवधि में अंतरिक्ष के एक समारोह के रूप में तरंग जेड की भयावहता को दर्शाता है t = t ₀ - हम इसे Z (x, t ₀ ) के रूप में रिकॉर्ड करते हैं। अंतरिक्ष में तरंग को ट्रैक करते हुए, हम देखते हैं कि यह आगे और पीछे की ओर झुकता है, और Z समय-समय पर बढ़ता और घटता है। किसी भी समय, लहर अंतरिक्ष में दोलन करती है।

ध्यान दें कि Z का भौतिक दूरी से कोई संबंध नहीं है। यह रस्सी की ऊंचाई हो सकती है, जैसा कि अंजीर में है। 2, या यह कुछ पूरी तरह से अलग हो सकता है, उदाहरण के लिए, अंतरिक्ष और समय में एक निश्चित बिंदु पर हवा का तापमान या चुंबक के एक निश्चित स्थान पर चुंबकीय परमाणु का उन्मुखीकरण। लेकिन एक्स अभी भी भौतिक दूरी का प्रतिनिधित्व करता है, और टी समय है।

इस लहर के शॉट, जेड (एक्स, टी ₀ ) में तीन दिलचस्प गुण हैं, जिनमें से दो एक वसंत पर एक गेंद पर भी लागू होते हैं।

1. रिज पर सबसे बड़े Z मान और डिप्रेशन में सबसे छोटे Z मान के बीच बीच में एक संतुलन मूल्य Z _{0 होता} है। अधिकांश समय हम तरंगों का अध्ययन करते हैं जिसके लिए Z ₀ = 0, क्योंकि अक्सर मान Z ₀ कोई फर्क नहीं पड़ता - लेकिन हमेशा नहीं।
2. तरंग में एक आयाम A है, जिसके द्वारा Z, संतुलन मूल्य से प्रत्येक रिज के शीर्ष पर या प्रत्येक अवसाद के नीचे समान मान से बदलता है।
3. लहर की एक लंबाई है - आसन्न लकीरों के बीच की दूरी λ, या, पड़ोसी गर्तों के बीच, या, जो समान है, जो समान है, आसन्न रिज और गर्त के बीच की दुगुनी दूरी। यह उसी तरह से अंतरिक्ष में दोलनों का वर्णन करता है कि एक अवधि (1 / आवृत्ति के बराबर) एक वसंत पर एक गेंद के समय में दोलन का वर्णन करता है।


अंजीर। 4

अंजीर में हमें क्या रूप याद दिलाता है। 3? यह साइन या कोसाइन फ़ंक्शन के ग्राफ़ जैसा दिखता है - अंजीर देखें। 4, जहां cos (w) को w पर प्लॉट किया गया है। कॉस (w) एक दोलन क्रिया है, जिसका शून्य में स्पष्ट संतुलन स्थिति है, इसका आयाम 1 है, और तरंग दैर्ध्य 2π है। अंजीर से कैसे जाएं अंजीर में लहर के लिए 4 सूत्र। 3? सबसे पहले, हम ए से गुणा (डब्ल्यू) करते हैं, ताकि आयाम ए के बराबर हो। फिर हम इसे वांछित संतुलन में बदलने के लिए पूरे सूत्र में जेड ₀ जोड़ते हैं (यदि ए = 0 है, तो कोई दोलन नहीं है, और सब कुछ बिंदु Z = Z पर टिकी हुई है _० )। और अंत में, w को 2πx / λ से बदलें, क्योंकि cos (w) में w = 0 और w = 2 at पर लकीरें होती हैं, इसलिए cos (2πx / λ) पर, लकीरें x = 0 और x = λ पर होंगी। सब मिलकर यह हमें देता है

$$

$$Z (x, t_0) = Z_0 + A cos (2 \ pi x / \ lambda)$$

यह लगभग वही सूत्र है जिसने समय पर एक गेंद पर एक गेंद की गति का वर्णन किया:

$$

$$z (t) = z_0 + A cos (2 \ pi \ n t t) = z_0 + A cos (2 \ pi t / T)$$

जहां ν दोलन आवृत्ति है, और T = 1 / ν दोलन अवधि है। सादृश्य देखें: एक अवधि समय को संदर्भित करती है क्योंकि एक तरंग दैर्ध्य अंतरिक्ष को संदर्भित करता है।

जारी रखने से पहले एक और ध्यान दें। मैं भी लिख सकता है:

$$

$$Z (x, t_0) = Z_0 + A cos (- 2 \ pi x / \ lambda)$$

चूंकि cos [w] = cos [-w]। तथ्य यह है कि हम तरंग फार्मूले में माइनस को आसानी से प्रतिस्थापित कर सकते हैं बाद में महत्वपूर्ण होगा।

एक विशिष्ट स्थान पर एक अंतहीन लहर के लिए फॉर्मूला

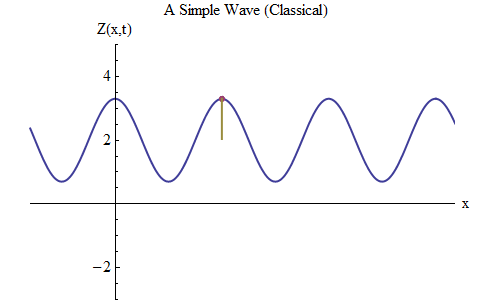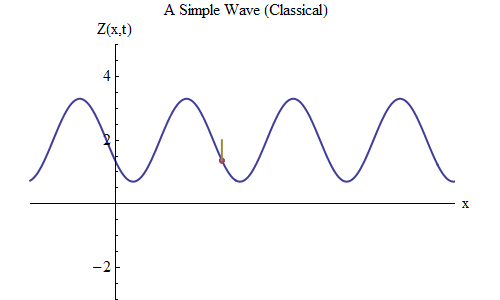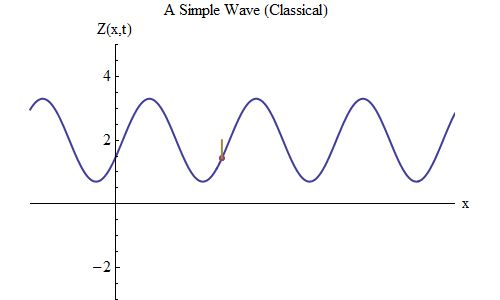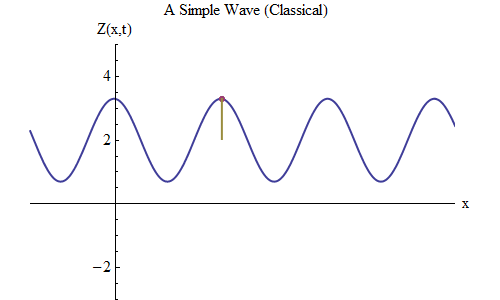अंजीर। 5

अब चलो एक और प्रश्न पूछते हैं: चलो देखते हैं कि लहर समय में कैसे बदलती है, रस्सी पर एक निश्चित बिंदु को ट्रैक करना, और देखें कि यह कैसे व्यवहार करता है और चलता है। यह अंजीर में दिखाया गया है। 5: वहाँ मैंने एक विशिष्ट बिंदु x ₀ निर्दिष्ट किया है, जो कि समय ₀ पर शिखा पर है। लहर दाईं ओर चलती है और बिंदु x ₀ पर तरंग Z के आकार का अनुसरण करती है, समय में परिवर्तन: Z (x ₀ , t)। और आप तुरंत देखेंगे कि एक निश्चित बिंदु पर लहर की ऊंचाई बिल्कुल वसंत पर एक गेंद की तरह व्यवहार करती है! इसलिए, यह आवृत्ति ν, या अवधि T = 1 / ν के एक फ़ंक्शन के रूप में, वसंत पर एक गेंद के समान बिल्कुल सूत्र होगा, जहां T उस क्षण के बीच का समय होता है जब x ₀ पर तरंग शिखा और क्षण पर होती है जब वह अगली बार फिर से शिखा के पास पहुंची।

$$

$$Z (x_0, t) = Z_0 + A cos (2 \ pi \ n t t) = Z_0 + A cos (2 \ pi t / T)$$

पूरा अनंत लहर फॉर्मूला

अब हमें Z (x, t) के लिए एक सूत्र की आवश्यकता है जो अंजीर में चित्रित लहर का वर्णन करता है। 3 और 5 (या किसी भी एक समान) किसी भी समय टी पर अंक x पर। सही उत्तर है:

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda)]$$

इसमें दोनों सूत्र शामिल हैं, समय में एक निश्चित बिंदु के लिए और अंतरिक्ष में एक निश्चित बिंदु के लिए।

एक्स के सामने माइनस साइन पर ध्यान दें। मैंने उल्लेख किया है कि Z (x, t ₀ ) के सूत्र में आप इच्छानुसार ऋण का स्थान ले सकते हैं। एक्स के सामने माइनस और टी के सामने एक प्लस के साथ, सूत्र एक लहर को दाईं ओर ले जाने का वर्णन करता है, जैसा कि एनिमेशन में। इसे सत्यापित करने के लिए, ध्यान दें कि जब t / T - x / λ = 0 होगा, तो तरंग एक शिखा होगी क्योंकि cos [0] = 1। जब t = 0, बिंदु x = 0 रिज पर। लेकिन अगर हम T / 10 से थोड़ा आगे, कहते हैं, तो शिखा बिंदु x = λ / 10 पर होगी, उस जगह के दाईं ओर जहां वह t = 0 पर थी - इसलिए शिखा (और पूरी लहर) दाईं ओर चलती है।

यदि आप Z (x, t) के लिए सूत्र में ऋण के बजाय एक प्लस रखते हैं तो क्या परिवर्तन होगा? फिर शिखा t / T + x / λ = 0 पर होगी, और इस मामले में, t = T / 10 पर, शिखा x = -λ / 10 पर होगी, उस स्थान के बाईं ओर जहां यह t = 0 पर था - जिसका अर्थ है , अब लहर बाईं ओर चलती है (चित्र 6)।


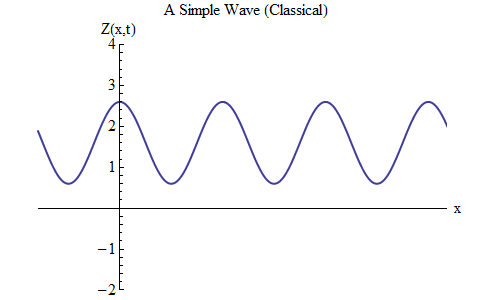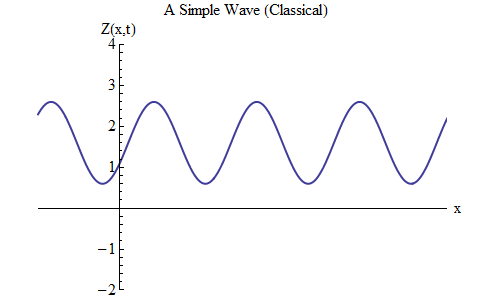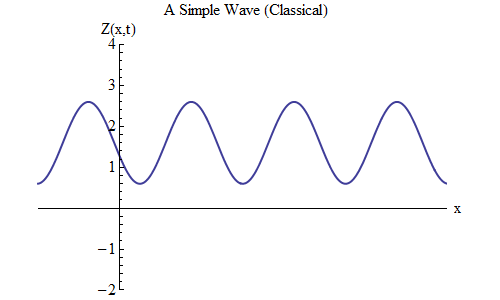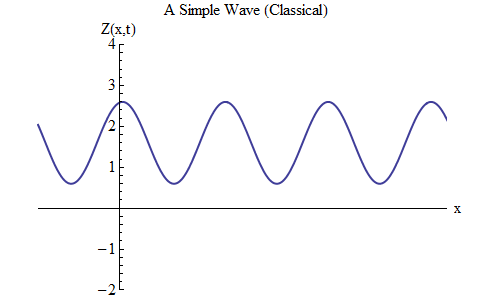अंजीर। 6

तरंगें, जो x और t के कार्य हैं, किसी भी दिशा में आगे बढ़ सकती हैं, इसलिए हमें बस दिए गए तरंग के लिए सही सूत्र चुनने की आवश्यकता है। सामान्यतया, जब हम तरंगों के साथ काम करते हैं, जो न केवल एक स्थानिक आयाम x के साथ आगे बढ़ सकती हैं, बल्कि तीनों निर्देशांक x, y और z के साथ, तब ये तरंगें किसी भी दिशा में जा सकती हैं, और हमें दिशा के आधार पर सही सूत्र चुनने की आवश्यकता होगी लहर की गति।

ठीक प्रिंट: हम टी के सामने माइनस साइन रख सकते हैं, और एक्स से पहले नहीं। लेकिन + t, + x -t, -x के समान है, क्योंकि यह कोसाइन के अंदर पूरे सूत्र को -1 से गुणा करने के बराबर होगा, और cos [w] = cos [-w]। इसलिए, + t, + x और -t, -x बाईं ओर जाने वाली एक तरंग देते हैं, और + t, -x -x और -t, + x एक तरंग को दाईं ओर ले जाते हैं।

वेव समीकरण

अब, जैसा कि एक वसंत पर एक गेंद के मामले में, जब हमने पहली बार गेंद के दोलन गति के लिए एक सूत्र पाया, और फिर गति के समीकरण को देखा, जिसके लिए यह सूत्र एक समाधान था, हम यहां भी ऐसा ही करेंगे। हमें लहर के आकार और गति के लिए एक सूत्र मिला। समाधान के बीच गति के किस समीकरण में ऐसा सूत्र है? हम अगले लेख में सीखते हैं।