हम कण भौतिकी को समझते हैं: 8) कैसे कण खेतों के साथ बातचीत करते हैं

कण भौतिकी को समझना:
1. एक वसंत पर गेंद, न्यूटोनियन संस्करण
2. एक वसंत पर एक क्वांटम गेंद
3. लहरें, क्लासिक लुक
4. लहरें, गति का शास्त्रीय समीकरण
5. क्वांटम तरंगें
6. फील्ड्स
7. कण क्वांटा हैं
8. कण खेतों के साथ कैसे संपर्क करते हैं

हिग्स फील्ड कैसे काम करता है:
1. मुख्य विचार

श्रृंखला के पिछले लेख में , मैंने समझाया कि प्रकृति के कण सापेक्ष क्षेत्र के क्वांटा हैं जो कक्षा 0 और वर्ग 1 के गति के समीकरणों को संतुष्ट करते हैं। लेकिन मैंने अभी तक जो नहीं कहा है, इसलिए यह कथन, सौभाग्य से, आंशिक रूप से सत्य है। वास्तविक समीकरण हमेशा थोड़ा और अधिक जटिल होते हैं, ताकि कणों और क्षेत्रों का परस्पर संबंध बना रहे, लेकिन बहुत अधिक विविध घटनाएं और प्रक्रियाएं संभव हो जाती हैं, जिसमें अन्य कणों की टक्कर के बाद कणों की उपस्थिति, कणों के अन्य कणों में क्षय और एक दूसरे से कणों का बिखरना शामिल है। साथ ही प्रोटॉन और न्यूट्रॉन, परमाणु नाभिक और परमाणुओं जैसी दिलचस्प वस्तुओं का निर्माण। मैं यह सब विस्तार से नहीं बता पाऊंगा, लेकिन इस लेख में मैं आपको एक परिचय दूंगा कि यह कैसे काम करता है।

समीकरणों के बीच मुख्य अंतर, जिसे मैंने "कक्षा 0" और "कक्षा 1" कहा, और समीकरण जो वास्तविक भौतिकी के लिए महत्वपूर्ण हैं, यह है कि वास्तविक समीकरणों में अतिरिक्त शब्द हैं जो दो या अधिक क्षेत्रों पर निर्भर करते हैं, और केवल एक नहीं । यह है, मान लीजिए कि सापेक्ष क्षेत्र Z (x, t) के लिए कक्षा 0 के समीकरण के बजाय, जो दिखता है

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

वास्तविक क्षेत्रों के लिए, समीकरण इस तरह दिखते हैं:

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = y 'Z (x, t) ^ 3 + y A (x, t) B (x, t)$$

जहाँ y और y 'संख्याएँ हैं (आमतौर पर 1 से कम), Z, Z (x, t) का छोटा अंकन है, और A (x, t) और B (x, t) अन्य क्षेत्रों की एक जोड़ी है। ऐसे समीकरणों में, कोई भी ऐसे शब्दों की उपस्थिति की उम्मीद कर सकता है जैसे ए (एक्स, टी) जेड (एक्स, टी), या ए (एक्स, टी) ² जेड (एक्स, टी), या जेड (एक्स, टी) ² , या ए भी। (x, t) d ² Z / dt ² , आदि। कौन से सदस्य कर सकते हैं और कौन नहीं दिख सकता है, इस प्रक्रिया में शामिल क्षेत्रों के विवरण पर निर्भर करता है। नियम सख्त हैं, बल्कि भ्रमित करने वाले हैं, इसलिए हम उनके लिए अभी नहीं जाएंगे। सामान्य तौर पर, हमारे द्वारा स्थापित प्रयोगों से (और सैद्धांतिक दृष्टिकोण से समझा जाता है) कि प्रकृति में:

• सिद्धांत में मान्य कोई शब्द (इलेक्ट्रिक चार्ज या आइंस्टीन के सापेक्षता के पत्राचार का संरक्षण) समीकरणों में प्रकट होता है,
• लेकिन कई क्षेत्रों वाले सदस्य आमतौर पर एक, दो, और कभी-कभी तीन क्षेत्रों (समय या स्थान के डेरिवेटिव वाले सदस्य भी आमतौर पर छोटे होते हैं) की तुलना में बहुत छोटे और महत्वहीन होते हैं।

इसलिए, अधिकांश दिलचस्प शारीरिक प्रक्रियाओं में, एक, दो या तीन क्षेत्रों के साथ सभी वैध शर्तों पर ध्यान केंद्रित किया जा सकता है।

थोड़ी शब्दावली। खेतों के साथ समीकरणों की शर्तों को पहली डिग्री में रैखिक कहा जाता है। हमारी कक्षा 0 या 1 समीकरणों के सभी शब्द रैखिक थे। दो या तीन क्षेत्रों वाले सदस्यों को द्विघात या घन कहा जाता है; सामान्य तौर पर, उन्हें नॉनलाइनर कहा जाता है। हमारी दुनिया की सभी रोचक घटनाएं गति के समीकरणों में अ-अस्पष्ट शब्दों के कारण दिखाई देती हैं - अर्थात्, एक-दूसरे के साथ और स्वयं के साथ खेतों की बातचीत। आइए उनमें से एक का अध्ययन करें।

अन्य दो के प्रतिध्वनि से एक नई लहर का उद्भव

यह जानने के लिए कि सब कुछ कितना दिलचस्प बन सकता है, हम तीन फ़ील्ड लेते हैं, ए (एक्स, टी), बी (एक्स, टी), सी (एक्स, टी), और एक सरलीकृत स्थिति। मान लीजिए कि फ़ील्ड A और B लगभग वर्ग 0 समीकरणों (और द्रव्यमान रहित क्वांटा) को संतुष्ट करते हैं, और फ़ील्ड C वर्ग 1 समीकरणों को संतुष्ट करता है (जिसमें न्यूनतम आवृत्ति ν _{मिनट के} साथ तरंगें होती हैं, और, तदनुसार, बड़े पैमाने पर m = h ν _मिनट / c ^{2 के} साथ क्वांटा, जहाँ h - प्लैंक स्थिरांक)। हम उनके समीकरणों में ग़ैर-शब्दों को भी जोड़ेंगे। विशेष रूप से, इस तरह (संक्षिप्तता के लिए, हम "ए (एक्स, टी)," और इसके बजाय "ए" लिखेंगे, सी प्रकाश की गति है, वाई एक संख्या है जो आमतौर पर 1 से कम है):

$$

$$d ^ 2A / dt ^ 2 - c ^ 2 d ^ 2A / dx ^ 2 = y BC \\ d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y AC \\ d 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y AB$$

ठीक प्रिंट: मैंने सभी तीन समीकरणों में ग़ैर-कानूनी शब्द जोड़े क्योंकि एक समीकरण में ऐसे शब्दों की उपस्थिति और दूसरे में उनकी अनुपस्थिति विरोधाभासों को जन्म देगी; उदाहरण के लिए, ऊर्जा का संरक्षण नहीं किया जाएगा। मैं जिस प्रक्रिया का वर्णन कर रहा हूं, उसके लिए हमें क्षेत्र C की गति के समीकरणों में केवल अरेखीय शब्दों पर विचार करना होगा।

आइए देखें कि ऐसे समीकरणों के सेट के साथ क्या होता है यदि फ़ील्ड ए की लहर फ़ील्ड बी की लहर से मिलती है। सिद्धांत रूप में, हम करीबी परीक्षा की विधि को लागू करके यह अनुमान लगा सकते हैं। यदि फ़ील्ड A में कोई तरंग है, तो A (x, t) इसके निकट नॉनज़रो है। जब फ़ील्ड A और B की तरंगें एक-दूसरे को ओवरलैप करती हैं, तो A (x, t) और B (x, t) को गुणा करने का परिणाम नॉनज़रो हो जाता है। अब हम सी के लिए समीकरण की ओर मुड़ते हैं: समय और स्थान में फ़ील्ड सी में परिवर्तन (बाईं ओर दो शब्द) उत्पाद ए और बी (दाईं ओर की शर्तों में से एक) के साथ जुड़े हुए हैं।

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

इसलिए भले ही A (x, t) B (x, t) फ़ील्ड शून्य शून्य हो, तो C (x, t) जल्द ही उसी सेक्शन में गैर-शून्य हो जाएगा। संक्षेप में, तरंगों ए और बी की बैठक के परिणामस्वरूप, फ़ील्ड सी की एक निश्चित छोटी गड़बड़ी होगी।

छोटा प्रिंट: आप में रुचि हो सकती है - सी के बाद गैर-शून्य हो जाता है, चाहे ए (एक्स, टी) सी (एक्स, टी) शब्द क्षेत्र के लिए गति के समीकरण में हो जाता है। यह क्षेत्र बी की अतिरिक्त गड़बड़ी का कारण बनता है। उत्तर हां है, लेकिन इसका प्रभाव होगा और भी छोटा। जब तक हम उसे अनदेखा नहीं करते, और बाद में पता चलता है कि ऐसा करने लायक क्यों था।

अंजीर में। चित्र 1 फ़ील्ड A (हरा) में एक आवृत्ति ν के साथ एक तरंग दिखाता है, जो फ़ील्ड B (नीला) में आवृत्ति तरंग ν के साथ होता है। मैंने सादगी और समरूपता के लिए आवृत्तियों को बराबर किया। बाद में हम देखेंगे कि अन्य मामले इस पर क्यों आते हैं। वेग ν का अनुमान हरी तरंग और अंतरिक्ष में एक बिंदु पर स्थित लंबवत रेखा और लहर के साथ दोलन करके लगाया जा सकता है।

नीचे दिया गया नारंगी उत्पाद उत्पाद A (x, t) B (x, t) दिखाता है; यह देखा जा सकता है कि दो तरंगों के सुपरिम्पोज होने पर यह नॉनजरो हो जाता है। यह भी देखा जाता है कि यह समय में भिन्न होता है। आप देख सकते हैं (इसे एक दोलन ऊर्ध्वाधर पट्टी के साथ तुलना करते हुए) कि ए (एक्स, टी) बी (एक्स, टी) दो बार तेजी से दोलन करता है। इस महत्वपूर्ण तथ्य को याद रखें। सामान्य स्थिति में, यदि एक आवृत्ति तरंग ν ₁ एक आवृत्ति तरंग ν _{2 से} मिलती है, तो उनका उत्पाद एक आवृत्ति ν _१ + ν _{२ के} साथ दोलन करेगा। और एक और बात: आप देख सकते हैं कि एबी कंपन दाएं या बाएं नहीं चलते हैं, वे जगह पर बने रहते हैं। बाद में हम देखेंगे कि यह महत्वपूर्ण क्यों है।


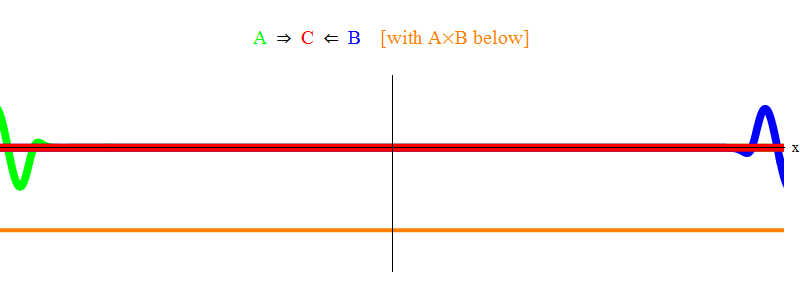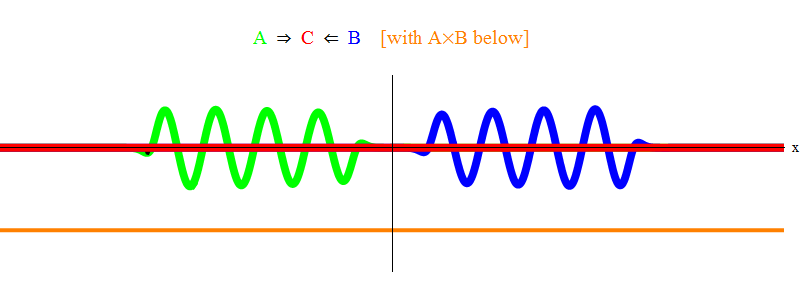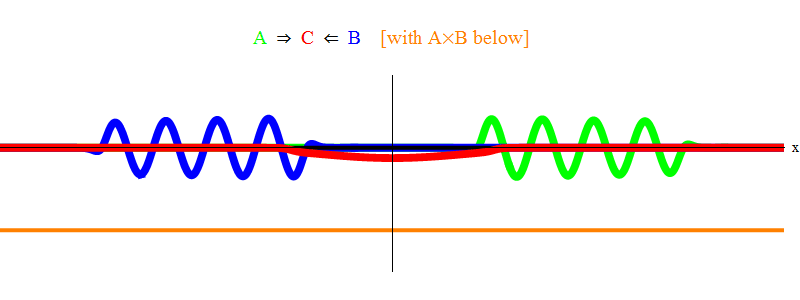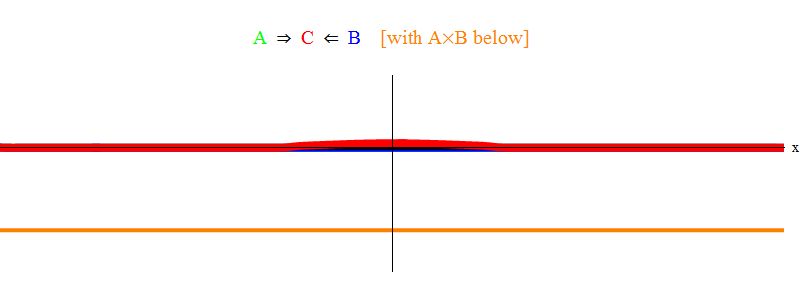अंजीर। 1

AB का गैर-शून्य मान C को कैसे प्रभावित करता है? उत्तर आवृत्ति ν पर अत्यधिक निर्भर है। पहले मैं आपको एक तैयार उत्तर दूंगा, और फिर कारण का एक अनुमानित विवरण। यह वास्तव में, प्रतिध्वनि है । अनुनाद तरंगों सहित सभी कंपन (कंपन) का एक अभिन्न घटना है। मैंने पहले ही वर्णन किया है कि वसंत पर गेंद एक प्राकृतिक आवृत्ति के साथ कैसे दोलन करती है, और गेंद को धक्का देने वाले कंपन बल को कैसे प्रतिध्वनित किया जा सकता है यदि बल के दोलन की आवृत्ति वसंत पर गेंद की प्राकृतिक आवृत्ति के साथ मेल खाती है।

अनुनाद को समझने के बाद, आप देखेंगे कि क्षेत्र C, एक न्यूनतम आवृत्ति और शून्य क्षैतिज गति के साथ दोलन करता है, एक वसंत पर गेंद की तरह व्यवहार करता है, और AB गेंद को दोलन बनाने की कोशिश कर रहे एक थरथराने वाले बल की तरह व्यवहार करता है। इसलिए, प्रतिध्वनि घटना तब होती है यदि कंपन आवृत्ति AB - 2ν - क्षेत्र C - ν _मिनट की न्यूनतम आवृत्ति है। अधिक विशेष रूप से:

• यदि 2 ν, ν _{मिनट के} बराबर नहीं है - यदि बल प्रतिध्वनि में नहीं है - तो उस क्षेत्र में जहां AB शून्य के बराबर नहीं है, C एक छोटे आयाम के साथ, अनियमित रूप से उतार-चढ़ाव करना शुरू कर देगा।
• यदि 2 ν = ν _मिनट - यदि बल प्रतिध्वनि में है - तो C एक बड़े आयाम के साथ सुचारू रूप से दोलन करेगा, उस क्षेत्र में जहां AB शून्य के बराबर नहीं है, और AB के शून्य होने पर भी उतार-चढ़ाव जारी रहेगा।

अंजीर। 1 केवल प्रतिध्वनि स्थिति को दर्शाता है 2 ν = ν _मिनट । यह देखा जा सकता है कि जब तरंग A तरंग B से होकर गुजरती है, तो वे एक स्थिर तरंग C के पीछे छोड़ती हैं, जो आवृत्ति ν _{मिनट के} साथ दोलन करती है। ठीक प्रिंट: अंजीर में। एक स्केच दिखाया गया है, समीकरणों का सटीक हल नहीं। सटीक समाधान में कई छोटे जटिल लक्षण होंगे जो मूल भौतिक अर्थ का निरीक्षण करेंगे, इसलिए मैंने उन्हें स्पष्टता के लिए हटा दिया। बाद में हम अनुनाद के बिना एक स्थिति पर विचार करेंगे, जो कि अधिक जटिल है, लेकिन भौतिकी के लिए भी अधिक महत्वपूर्ण है।

अन्य दो के विनाश से एक नए कण का उद्भव

मैंने आपसे केवल यह प्रदर्शित किया है कि समीकरण C में nonlinear शब्द AB, C की तरंगों के सुपर ए और B को क्षेत्र C के दोलनों का निर्माण करने का कारण बन सकता है यदि फ़ील्ड A और B की आवृत्तियों का योग फ़ील्ड C की न्यूनतम आवृत्ति के बराबर है लेकिन यदि ये तरंगें थीं बहुत छोटा आयाम? यदि फ़ील्ड A का एक क्वांटम फ़ील्ड B के एक क्वांटम से मिलता है तो क्या हो सकता है?

• यदि आवृत्तियाँ AB, C C के साथ प्रतिध्वनि में प्रवेश करती हैं, तो फ़ील्ड C की एक मात्रा हो सकती है, अर्थात एक वास्तविक कण C और क्वांटा A और B गायब हो जाएगा - "सर्वनाश"।
• इसके अलावा, क्वांटा ए और बी कण सी बनाने के बिना, बस एक दूसरे को पास कर सकते हैं
• क्वांटम यांत्रिकी के नियम बताते हैं कि कण C बनाने की संभावना y के वर्ग के आनुपातिक है, जो गति C के समीकरण में AB द्वारा गुणा किया जाता है।
• यदि आवृत्ति अनुनाद में प्रवेश नहीं करती है, तो वास्तविक कण C दिखाई नहीं देगा। हालाँकि, फ़ील्ड C में एक अस्थायी गड़बड़ी हो सकती है, जिसे अक्सर "आभासी कण" C कहा जाता है, इसका एक उदाहरण है, जिस स्थिति में क्वांटा A और B गायब हो सकते हैं। ऐसी गड़बड़ी का परिणाम क्या है? मैंने इस प्रक्रिया को लेख के अंत में "पूंछ" खंड में आंशिक रूप से वर्णित किया है।

यह चीजों की सामान्य स्थिति है। चलो विवरण में तल्लीन करते हैं।

कणों के लिए क्या है, अर्थात्, खेतों ए, बी और सी के क्वांटा का मतलब प्रतिध्वनि में होना है या प्रतिध्वनि में नहीं है? यह याद रखने योग्य है कि एक क्वांटम की ऊर्जा समीकरण E = h ν के कारण इसकी आवृत्ति से संबंधित है। इसलिए हम तरंगों की चर्चा को कणों की चर्चा में तब्दील करते हैं।

मान लीजिए कि खेतों ए और बी में हमारी लहरों में से प्रत्येक में एक मात्रा है। ये क्वांटा बड़े पैमाने पर होते हैं, क्योंकि ए और बी वर्ग 0. के समीकरणों को संतुष्ट करते हैं। अधिक सटीक रूप से, गति के उनके समीकरणों में रैखिक शब्द कक्षा 0. के समान हैं क्योंकि क्वांटा ए और बी की आवृत्ति समान होती है, उनकी ऊर्जा समान होती है, E = h ν। चूँकि एक द्रव्यमान रहित क्वांटम की गति p = E / c है, क्वांटा A और B का परिमाण h ν / c के बराबर होगा, लेकिन दिशा में विपरीत है, क्योंकि उनमें से एक बाईं ओर चलता है और दूसरा दाईं ओर। इसलिए:

• एक साथ दो क्वांटा की कुल ऊर्जा 2hν होगी।
• एक साथ दो क्वांटा की कुल गति शून्य होगी।

चूंकि ऊर्जा और संवेग संरक्षित होते हैं, दो क्वांटा की टक्कर के बाद की कुल ऊर्जा 2hν के बराबर रहेगी, और कुल पल शून्य रहेगा।

तरंगों के मामले में, हमने देखा कि चूंकि C के लिए समीकरण में AB AB का एक शब्द होता है, इसलिए एक प्रतिध्वनि होती है जब आवृत्ति AB (एक दोलन शक्ति के रूप में काम करना) न्यूनतम आवृत्ति C (एक स्प्रिंग पर गेंद की तरह काम करना) के साथ मेल खाती है। हम इस कथन को क्वांटा में अनुवादित करते हैं।

आवृत्ति AB 2 ν होगी, इसलिए उत्पाद A और B की ऊर्जा, जब तरंगों A और B में एक मात्रा होती है, ऊर्जा A और B के योग के बराबर होती है।

$$

$$E_ {AB} = 2 h \ nu = E_A + E_B$$

न्यूनतम आवृत्ति C, ν _{मिनट के} बराबर होती है, जिसका अर्थ है कि क्षेत्र C की एक स्थिर मात्रा के लिए, गति 0 है, और ऊर्जा

$$

$$E_C = h \ nu_ {min} = mc ^ 2$$

जहां m क्वांटम C का द्रव्यमान है।

अनुनाद के लिए, 2 ν = ν _मिनट की आवश्यकता होती है, जो है:

$$

$$E_A + E_B = 2 h \ nu = h \ nu_ {min} = mc ^ 2 = E_C$$

संक्षेप में, अनुनाद तब होता है जब कणों ए और बी (जिसमें हमारे मामले में दालों समान हैं और दिशा में विपरीत हैं) के बराबर ऊर्जा की मात्रा बस एक स्थिर कण सी बनाने के लिए पर्याप्त हैं! इस प्रक्रिया में, कणों ए और बी को नष्ट कर दिया जाता है - उनकी ऊर्जा पूरी तरह से कण सी बनाने में जाती है। यह (योजनाबद्ध रूप से) अंजीर में दिखाया गया है। 2, जिसे आपको अंजीर के साथ तुलना करने की आवश्यकता है। 1।


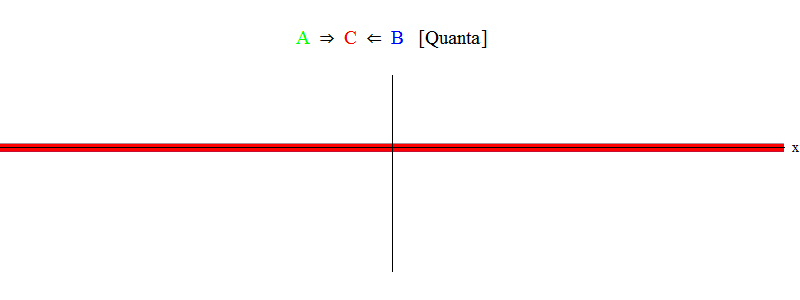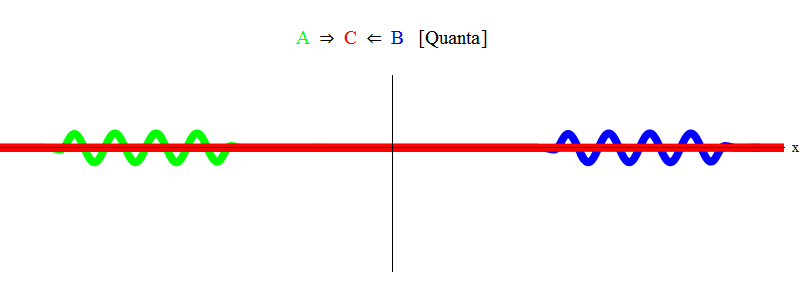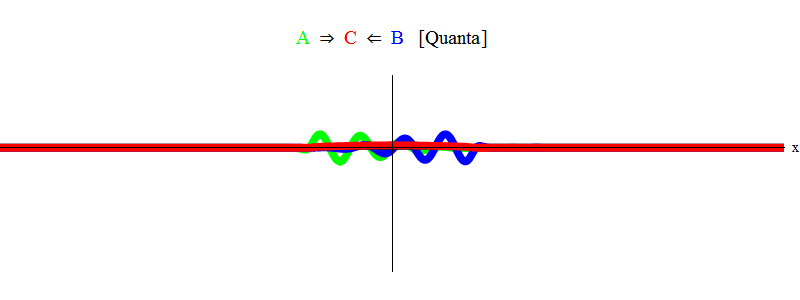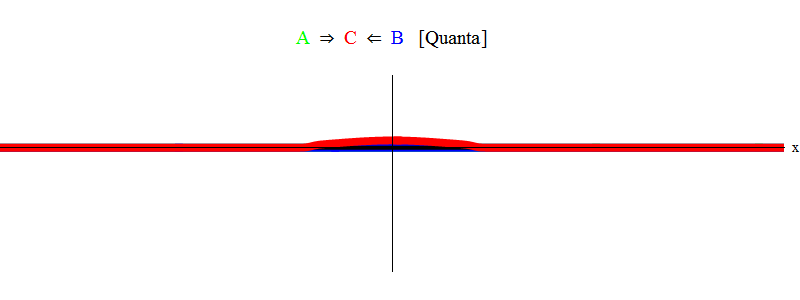अंजीर। 2

विचार

मैंने आपको केवल ए + बी → सी। की प्रक्रिया दिखाई। मेरे स्पष्टीकरण में, मैंने भ्रम से बचने के लिए तीन अलग-अलग प्रकार के कणों का उपयोग किया। लेकिन एक ही विचार एक को A + A → C (उदाहरण के लिए, gluon + gluon → Higgs कण) की प्रक्रियाओं से गुजरने की अनुमति देता है, और मूल रूप से यह है कि बड़े Hadron कोलाइडर में Higgs कण कैसे प्राप्त होता है) और A + A * → C, जहाँ A * के रूप की प्रक्रियाएँ होती हैं। - ए के लिए एंटीपार्टिकल (उदाहरण के लिए, क्वार्क + एंटिकार्क → जेड-कण, और यह कैसे जेड-कण आमतौर पर एलएचसी पर प्राप्त होता है)। यह केवल मामूली विवरण बदलने के लिए आवश्यक है, लेकिन सार समान रहता है।

एक और प्रक्रिया जो समान विचार का प्रतिनिधित्व करती है, केवल समय में उलट जाती है - कणों का क्षय। हिग्स कण का क्षय दो फोटोन या जेड कणों में एक क्वार्क में होता है और एक एंटीक्वार्क अनिवार्य रूप से अंजीर में एनीमेशन के रूप में होता है। २, विपरीत दिशा में जाना।

अवशेष

1. यदि AB प्रतिध्वनि के बिना AB शब्द को क्षेत्र C से घटा देता है - यदि 2 ν _min ν _मिनट - क्या होगा? आप याद कर सकते हैं कि यदि आप गलत आवृत्ति पर बच्चे के साथ स्विंग को धक्का देते हैं, या वसंत पर गेंद के लिए एक बल लगाते हैं, तो एक आवृत्ति के साथ दोलन होता है जो कंपन की प्राकृतिक आवृत्ति के साथ मेल नहीं खाता है, आपको एक छोटे आयाम के साथ असमान कंपन मिलेगा। वर्तमान संदर्भ में, फ़ील्ड सी के साथ एक ही बात होती है। फ़ील्ड सी किसी भी तरह का व्यवहार करेगा, लेकिन इससे एक अच्छी तरह से व्यवहार करने वाले क्वांटम सी की उपस्थिति नहीं होगी। यह बस थोड़ा चिंतित हो जाता है। यह बुरा आक्रोश तथाकथित का एक उदाहरण है "वर्चुअल कण C" - लेकिन यह एक कण नहीं है (इसके नाम के बावजूद फ़ील्ड C की एक तरंग की मात्रा)। इसका द्रव्यमान कण C के द्रव्यमान से भिन्न होता है; यह बड़ा या छोटा हो सकता है। कण सी के विपरीत, यह लंबे समय तक अपने आप से मौजूद नहीं है। और यह उन आयाम स्थितियों को संतुष्ट नहीं करता है जो वास्तविक क्वांटा को संतुष्ट करना चाहिए। इसके बजाय, कण सी के विपरीत, जो कुछ समय के लिए मौजूद है, अंजीर के साथ। 2, एक गैर-प्रासंगिक गड़बड़ी केवल तब मौजूद होती है जब A चौराहे बी।

लेकिन इसका मतलब यह नहीं है कि यह किसी भी चीज को प्रभावित नहीं करता है। उदाहरण के लिए, यह कणों ए और बी को एक दूसरे से उछाल दे सकता है।

$$

$$A_ \ rightarrow + B_ \ leftarrow → C_ {आक्रोश} → A_ \ leftarrow + B_ \ rightarrow$$

सामान्य तौर पर, त्रि-आयामी अंतरिक्ष में, एक पलटाव, या बिखरने, इस तथ्य को जन्म दे सकता है कि ए किसी भी दिशा में चलता है और बी विपरीत दिशा में चलता है। ऐसी प्रक्रियाओं के उदाहरणों में एक आभासी फोटॉन के कारण इलेक्ट्रॉन और पॉज़िट्रॉन बिखरना, या एक आभासी ग्लूऑन के कारण क्वार्क और एंटीक्वार्क बिखरना शामिल हैं।

अन्य क्षेत्रों की उपस्थिति में, डी और ई, सी के साथ बातचीत और गति सी के समीकरण में भाग लेते हैं

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B + y 'D E$$

बहुत अधिक रोचक प्रक्रियाएँ हो सकती हैं:

ए + बी → सी _{गड़बड़ी} → डी + ई

यह सही है: कण ए और बी आभासी कण सी के लिए धन्यवाद का सफाया कर सकते हैं, और नए कणों की उपस्थिति का नेतृत्व कर सकते हैं डी और ई। यह नया कण बनाने का दूसरा तरीका है! उदाहरण के लिए, एक इलेक्ट्रॉन एक पॉज़िट्रॉन के साथ टकरा सकता है, एक आभासी फोटॉन के माध्यम से मिटा सकता है (याद रखें कि इसका मतलब है "एक आवृत्ति पर फोटॉन फ़ील्ड के एक गड़बड़ी के माध्यम से जो गुंजयमान यंत्र के साथ मेल नहीं खाता"), और एक म्यूऑन और एंटीमून, या क्वार्क और एंटीक्वार्क में बदल जाता है। निचले क्वार्क और ऊपरी एंटिकार्क एक आभासी डब्ल्यू-कण के माध्यम से टकरा सकते हैं, और एक इलेक्ट्रॉन और एक एंटीन्यूट्रिनो में बदल सकते हैं। या दो ग्लून्स टकरा सकते हैं, एक आभासी ग्लोन के माध्यम से नष्ट कर सकते हैं, और एक ऊपरी क्वार्क और एक ऊपरी एंटीकार्क में बदल सकते हैं (यह एलएचसी पर ऊपरी क्वार्क प्राप्त करने का सबसे आम तरीका है)।

2. क्या होगा अगर खेतों ए और बी में दो तरंगों में अलग-अलग आवृत्तियां होती हैं, ν _ए और ν _बी ? उपयुक्त आवृत्तियों पर, कण C अभी भी दिखाई दे सकते हैं, लेकिन अनुनाद की स्थितियां भिन्न होंगी, और निर्मित कण C स्थिर नहीं होगा। चलिए इसका पता लगाते हैं।

यदि उनके पास अलग-अलग आवृत्तियां हैं, तो दो टकराने वाले मासलेस क्वांटा होंगे

• विभिन्न ऊर्जाएँ $$$E_A = h \ nu_A$ और $$$E_B = h \ nu_B$
• विभिन्न आवेगों $$$p_A = + h \ nu_A / c$ और $$$p_B = - h \ nu_B / c$ (यहां, प्लस का अर्थ दाईं ओर, बाईं ओर माइनस है)।

कुल गति p _A + p _B अब नॉनजरो है। लेकिन रफ्तार बरकरार है। इसलिए, यदि कण A और B के विलोपन के परिणामस्वरूप कण C हो सकता है, तो इसमें एक गति p _C = p _A + p _{B होगा} , इसलिए यह बाएँ या दाएँ जाएगा, और स्थिर नहीं रहेगा। यदि ν _ए > ν _बी , तो यह दाईं ओर जाएगा, अन्यथा, बाईं ओर।

मूविंग पार्टिकल C बनाने के लिए कितनी ऊर्जा की आवश्यकता होती है? इसके लिए, एक स्थिर एक की तुलना में अधिक ऊर्जा की आवश्यकता होती है - किसी भी विशाल कण की तरह, इसकी ऊर्जा और गति को संतुष्ट करना होगा

$$

$$E_C ^ 2 = (p_Cc) ^ 2 + (mc ^ 2) ^ 2$$

जिसका अर्थ है कि E _C = mc ² यदि p _C = 0, या इससे अधिक है यदि गति नॉनजरो है। ऊर्जा और संवेग के संरक्षण का नियम हमें बताता है कि:

$$

$$E_C = E_A + E_B$$

$$

$$p_C = p_A + p_B = E_A / c - E_B / c$$

मुझे अंतिम समीकरण कहां से मिला? एक द्रव्यमान रहित कण, p = E / c के लिए, और हमारे टकराने वाले कणों A और B के लिए, उनका संवेग विपरीत होता है, इसलिए वे संकेत में भिन्न होते हैं। पिछले समीकरण में इसे प्रतिस्थापित करें और प्राप्त करें:

$$

$$(E_A + E_B) ^ 2 = (E_A - E_B) ^ 2 + (mc ^ 2) ^ 2$$

E _A ² और E _B ² शब्द परस्पर विलोपित हैं, और E E E _B को बाईं ओर ले जाने पर, हम निम्नलिखित हैं:

$$

$$4 E_A E_B = (mc ^ 2) ^ 2$$

एच ^{2 से} विभाजित करना और संबंध एम = एचपीओ _मिनट / सी ² का उपयोग करके, हम प्रतिध्वनि स्थिति प्राप्त करते हैं:

$$

$$(2 \ nu A) (2 \ nu B) = \ nu_ {min} ^ 2$$

जो सही ढंग से कम हो जाता है जब ν _A = ν _B एक गतिहीन कण C, 2 ν = ν _मिनट के समीकरण के लिए। यदि यह स्थिति संतुष्ट नहीं है, तो कण C नहीं बनाया जा सकता है। अगर संतुष्ट हैं, तो यह संभव है।

3. मैंने नोट किया कि जिस तरह से फ़ील्ड C के लिए गति के समीकरण में AB शब्द होता है, उसी तरह B के समीकरण में AC शब्द होता है। इन समीकरणों को याद करें:

$$

$$d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y A C$$

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

इसलिए, यदि तरंगों का सुपर ए और बी क्षेत्र C में एक लहर की उपस्थिति की ओर जाता है, तो इसे अंजीर बना देता है, जैसा कि अंजीर में है। 1, क्या हमें इस तथ्य के बारे में चिंता करने की ज़रूरत है कि यह नई लहर C मौजूदा लहर A के साथ ओवरलैप करती है और फ़ील्ड B में परिवर्तन की ओर ले जाती है? मैंने जवाब दिया कि "हां, लेकिन हम इसे नजरअंदाज कर सकते हैं।" हम दो कारणों के संयोजन के कारण उपेक्षा कर सकते हैं।

सबसे पहले, एबी और बीसी के गुणकों से पहले प्रदर्शित होने वाली संख्या "वाई" के कारण। सदस्य AB के क्षेत्र C पर प्रभाव B के गुणा के अनुपात के अनुसार होता है। B के सदस्य AC के क्षेत्र B पर प्रभाव भी C से गुणा करने के लिए आनुपातिक होता है, लेकिन यह बदले में y से ² गुणा के बराबर होगा। B द्वारा A को गुणा किया जाता है। जब तक y 1 से कम है, y ² , y से कम होगा, इसलिए, AB सदस्य के C पर प्रभाव की तुलना में AC सदस्य के B पर प्रभाव छोटा है - कम से कम छोटी तरंगों A और B के अभ्यास के लिए, ये लहरें आमतौर पर छोटी होती हैं: कण A, क्षेत्र A में तरंग की एक मात्रा है; इसलिए, तरंग A में छोटे आयाम हैं घ।

जिसमें से दूसरा, अजनबी, लेकिन अधिक ठोस कारण इस प्रकार है: हमने देखा कि यदि एक क्वांटम ए एक क्वांटम बी से मिलता है और एक क्वांटम सी में बदल जाता है, तो ए और बी तरंगें गायब हो जाती हैं (सत्यानाश)। C के निर्माण के बाद, अब कोई तरंग A नहीं है, इसलिए AC शून्य है, अर्थात फ़ील्ड B पर कोई प्रभाव नहीं पड़ता है।

और अंतिम कैच: हालांकि मैं अतिरिक्त गणना के बिना यह साबित नहीं कर सकता, भले ही ए और बी तरंगों में एक क्वांटम शामिल हो, जैसा कि अंजीर में है। 2, फिर अंजीर में प्रक्रिया। 2 अधिक जटिल होगा यदि y 1. की तुलना में बहुत बड़ा था। तो मैंने जो कहानी बताई है उसकी सादगी के लिए y के छोटे मूल्यों की आवश्यकता होती है। प्रकृति में, कण भौतिकी में बहुसंख्यक गैर-रेखीय शब्द आमतौर पर छोटे होते हैं, इसलिए मैंने जो कहा वह सबसे व्यावहारिक रूप से लागू स्थितियों पर लागू होता है। अपवाद बहुत दिलचस्प हैं - वे प्रोटॉन और अन्य हैड्रॉन के रूप में इस तरह की जटिल वस्तुओं के निर्माण का नेतृत्व करते हैं।