 मौजूदा प्रणाली में दो उलझे हुए फोटॉनों को बनाकर, और उन्हें एक बड़ी दूरी पर विभाजित करके, हम उनमें से एक की स्थिति के बारे में जानकारी प्राप्त कर सकते हैं
मौजूदा प्रणाली में दो उलझे हुए फोटॉनों को बनाकर, और उन्हें एक बड़ी दूरी पर विभाजित करके, हम उनमें से एक की स्थिति के बारे में जानकारी प्राप्त कर सकते हैंक्वांटम भौतिकी पहेली से भरा है, हमारे अंतर्ज्ञान के विरोध के लिए कुख्यात है। कणों को यह पता लगता है कि आप उन्हें देख रहे हैं या नहीं और अलग-अलग व्यवहारों को प्रदर्शित करते हैं, इस पर निर्भर करता है कि आप उन्हें देख रहे हैं या नहीं, एक डबल भट्ठा से गुजरते हुए। एक मात्रा की माप, उदाहरण के लिए, एक कण की स्थिति, पूरक मात्रा में अपनी अंतर्निहित अनिश्चितता पैदा करती है, उदाहरण के लिए, गति। और यदि आप इसके स्पिन को ऊर्ध्वाधर दिशा में मापते हैं, तो क्षैतिज दिशा में पीछे की जानकारी को नष्ट कर दें। लेकिन सभी क्वांटम परिघटनाओं में से सबसे "भयावह" क्वांटम उलझाव होगा, जब एक कण तुरंत "पता" लगता है कि क्या इसके साथ भ्रमित होने वाले साथी को मापा गया था, भले ही यह ब्रह्मांड के दूसरे छोर पर किया गया हो। इस सप्ताह हम पाठक के प्रश्न को देखेंगे, इस बात से जुड़े कि इसे आम तौर पर एक रहस्य क्यों माना जाता है।
फोटॉनों के दृष्टिकोण से, उन्होंने शून्य समय में एक शून्य दूरी की यात्रा की। तो इसमें डरने की क्या बात है? जब तक उनमें से एक को मापा नहीं जाता है, तब तक वे एक ही स्थान पर और एक ही समय में होते हैं (यदि आप उन्हें मानते हैं), तो इसे एक रहस्य नहीं कहा जा सकता है कि वे अपने राज्यों का समन्वय करते हैं।
उचित तर्क: तेजी से बढ़ने वाले कणों के लिए समय के फैलाव का मतलब है कि वे अपने राज्यों को किसी भी गति से समन्वयित कर सकते हैं। लेकिन इस पहेली को हल करना इतना आसान नहीं है।
 क्वांटम nonlocality को सत्यापित करने के लिए तीसरे Aspe प्रयोग की योजना। स्रोत से उलझे हुए फोटॉनों को दो स्विचों में भेजा जाता है जो उन्हें ध्रुवीकरण करने वाले सेंसरों के लिए निर्देशित करते हैं। स्विच बहुत जल्दी अपने राज्यों को स्विच करते हैं, फोटॉनों की उड़ान के दौरान डिटेक्टर सेटिंग्स को बदलते हैं।
क्वांटम nonlocality को सत्यापित करने के लिए तीसरे Aspe प्रयोग की योजना। स्रोत से उलझे हुए फोटॉनों को दो स्विचों में भेजा जाता है जो उन्हें ध्रुवीकरण करने वाले सेंसरों के लिए निर्देशित करते हैं। स्विच बहुत जल्दी अपने राज्यों को स्विच करते हैं, फोटॉनों की उड़ान के दौरान डिटेक्टर सेटिंग्स को बदलते हैं।सबसे पहले, चलिए उलझने के मुद्दे पर चलते हैं। प्रयोग आमतौर पर फोटॉनों के साथ किया जाता है: आप एक विशेष सामग्री (बिखरने वाले क्रिस्टल) के माध्यम से प्रकाश की एक मात्रा को प्रसारित करते हैं, इसे दो फोटॉन में विभाजित करते हैं। ये फोटॉन एक निश्चित अर्थ में उलझे रहेंगे, यानी अगर किसी के पास एक स्पिन है, तो आंतरिक कोणीय गति +1 है, तो दूसरे में -1 होगा। लेकिन जो हमारे लिए अज्ञात है। आप ऐसे प्रयोगों को भी कर सकते हैं, जिनमें बड़ी संख्या में फोटॉनों पर विचार करने के बाद, के बीच का अंतर
• सांख्यिकीय परिणाम यदि स्पिन +1,
• सांख्यिकीय परिणाम यदि स्पिन -1 है,
• यदि स्पिन अपरिभाषित रहता है तो सांख्यिकीय परिणाम।
इन परिणामों की कल्पना करना बहुत मुश्किल है, लेकिन क्वांटम यांत्रिकी में एक अद्भुत सादृश्य है: एक कण का दोहरा अंतराल से गुजरना।
 यदि इलेक्ट्रॉनों, फोटॉनों, या किसी अन्य कण को एक दोहरे अंतराल के माध्यम से पारित किया जाता है, तो एक हस्तक्षेप पैटर्न उत्पन्न होता है। लेकिन यह केवल तभी होता है जब आप जांच नहीं करते हैं कि वे किस अंतराल से गुजरते हैं!
यदि इलेक्ट्रॉनों, फोटॉनों, या किसी अन्य कण को एक दोहरे अंतराल के माध्यम से पारित किया जाता है, तो एक हस्तक्षेप पैटर्न उत्पन्न होता है। लेकिन यह केवल तभी होता है जब आप जांच नहीं करते हैं कि वे किस अंतराल से गुजरते हैं!यदि आप एक कण को डबल स्लिट के माध्यम से पास करते हैं - वह है, दो संकीर्ण स्लॉट वाली एक स्क्रीन जो एक-दूसरे के बहुत करीब हैं - और यह उनके माध्यम से गुजरता है, स्क्रीन द्वारा आयोजित होने के बजाय, आप आसानी से यह निर्धारित कर सकते हैं कि यह दूसरी तरफ कहां होगा। यदि आप एक डबल पॉट के माध्यम से एक समय में कई कणों को लॉन्च करते हैं, तो आप पाएंगे कि दरार से गुजरने वाले कण एक हस्तक्षेप पैटर्न बनाते हैं। दूसरे शब्दों में, प्रत्येक कण ऐसा व्यवहार नहीं करता है जैसे कि वह एक या दूसरे अंतराल से गुजरा हो; वह ऐसा व्यवहार करती है जैसे वह एक ही बार में दोनों स्लॉट से गुजरती है, एक तरंग के रूप में खुद के साथ हस्तक्षेप करती है, और चलती रहती है।
लेकिन यह चित्र, जो ब्रह्मांड के सभी कणों के अजीब क्वांटम-यांत्रिक प्रकृति को प्रदर्शित करता है, केवल तभी प्रकट होता है जब आप यह निर्धारित नहीं करते हैं कि कण किस अंतराल से गुजरता है।
 यदि आप यह निर्धारित करते हैं कि एक कण किस अंतराल से गुजरता है, तो शेष प्रयोग को अपरिवर्तित छोड़ दें, तो आपको एक हस्तक्षेप चित्र बिल्कुल नहीं मिलेगा।
यदि आप यह निर्धारित करते हैं कि एक कण किस अंतराल से गुजरता है, तो शेष प्रयोग को अपरिवर्तित छोड़ दें, तो आपको एक हस्तक्षेप चित्र बिल्कुल नहीं मिलेगा।यदि इसके बजाय आप एक कण को मापते हैं क्योंकि यह स्लॉट्स में से एक से गुजरता है - यह एक काउंटर स्थापित करके किया जा सकता है - आपको एक हस्तक्षेप चित्र नहीं मिलेगा। आपको स्लॉट 1 से गुजरने के लिए कणों का एक गुच्छा मिलेगा, और स्लॉट 2 के लिए एक गुच्छा होगा।
 इलेक्ट्रॉनों की तरंग पैटर्न एक समय में एक डबल गैप से गुजरती है। यदि आप मापते हैं कि इलेक्ट्रॉन किस अंतराल से गुजरा है, तो आप क्वांटम हस्तक्षेप चित्र को नष्ट कर देते हैं। ध्यान दें कि ऐसी तस्वीर बनाने के लिए एक से अधिक इलेक्ट्रॉनों की आवश्यकता होती है।
इलेक्ट्रॉनों की तरंग पैटर्न एक समय में एक डबल गैप से गुजरती है। यदि आप मापते हैं कि इलेक्ट्रॉन किस अंतराल से गुजरा है, तो आप क्वांटम हस्तक्षेप चित्र को नष्ट कर देते हैं। ध्यान दें कि ऐसी तस्वीर बनाने के लिए एक से अधिक इलेक्ट्रॉनों की आवश्यकता होती है।दूसरे शब्दों में, एक माप लेने से जो कण द्वारा चुने गए मार्ग को निर्धारित करता है, आप इस पसंद का परिणाम बदलते हैं! एक कण के लिए, आप केवल भट्ठा 1, भट्ठा 2 या स्वयं के हस्तक्षेप से गुजरने की संभावना निर्धारित कर सकते हैं। आपके प्रयोग की वास्तविक स्थिति का पता लगाने के लिए अधिक आँकड़ों की आवश्यकता होगी।
 आधे-पूर्णांक स्पिन कणों के लिए बेल क्वांटम मैकेनिकल टेस्ट
आधे-पूर्णांक स्पिन कणों के लिए बेल क्वांटम मैकेनिकल टेस्टभ्रामक फोटॉनों पर वापस। या किसी भी उलझे हुए कणों के लिए सामान्य रूप से। आप दो उलझे हुए कण बनाते हैं, जिसमें आप उनके गुणों की कुल मात्रा जानते हैं, लेकिन उनमें से प्रत्येक के गुण नहीं। सबसे सरल उदाहरण एक स्पिन होगा - दो फोटॉनों के लिए यह या तो (+1 और -1) या (-1 और +1), दो इलेक्ट्रॉनों के लिए - (+ ½ और -½) या (-½ और + ½) - और आप बाहर हो जाएगा आप यह नहीं जानते कि आपके पास कौन सा स्पिन होगा, जब तक आप इसे माप नहीं लेते। अंतराल के बजाय, आप उन्हें एक पोलराइज़र के माध्यम से भेज सकते हैं। और जैसे ही आप एक को मापते हैं, आप दूसरे को निर्धारित करते हैं। दूसरे शब्दों में, आप इसे तुरंत जानते हैं।
 एक क्वांटम इरेज़ प्रयोग जिसमें दो उलझे हुए कण अलग और मापे जाते हैं। गंतव्य पर कणों में से एक पर कोई कार्रवाई दूसरे को प्रभावित नहीं करती है।
एक क्वांटम इरेज़ प्रयोग जिसमें दो उलझे हुए कण अलग और मापे जाते हैं। गंतव्य पर कणों में से एक पर कोई कार्रवाई दूसरे को प्रभावित नहीं करती है।"भयावह" तथ्य यह है कि भौतिकी में तुरंत और कुछ नहीं होता है। किसी भी सिग्नल की उच्चतम संचरण गति, वैक्यूम में प्रकाश की गति के बराबर होगी। लेकिन इन दो उलझे हुए कणों को मीटर, किलोमीटर, खगोलीय इकाइयों या प्रकाश वर्ष में विभाजित किया जा सकता है, और उनमें से एक को मापना तुरंत दूसरे की स्थिति को निर्धारित करता है। इससे कोई फर्क नहीं पड़ता कि उलझे हुए कण प्रकाश की गति से चलते हैं या नहीं, उनमें द्रव्यमान है या नहीं, उनमें कितनी ऊर्जा है, और यदि आप उन्हें एक-दूसरे से अलग करते हैं ताकि वे एक-दूसरे को फोटॉन न भेजें। ऐसी कोई खामियां नहीं हैं जो किसी भी संदर्भ प्रणाली में बातचीत की गति को किसी भी तरह से इसके लिए क्षतिपूर्ति करने की अनुमति देती हैं। 1990 के दशक के उत्तरार्ध में, इन कणों के पृथक्करण और एक साथ माप के प्रयोगों ने निर्धारित किया कि यदि उनके बीच कोई सूचना प्रसारित की जाती है, तो यह प्रकाश की गति से 10,000 गुना तेज चलती है।
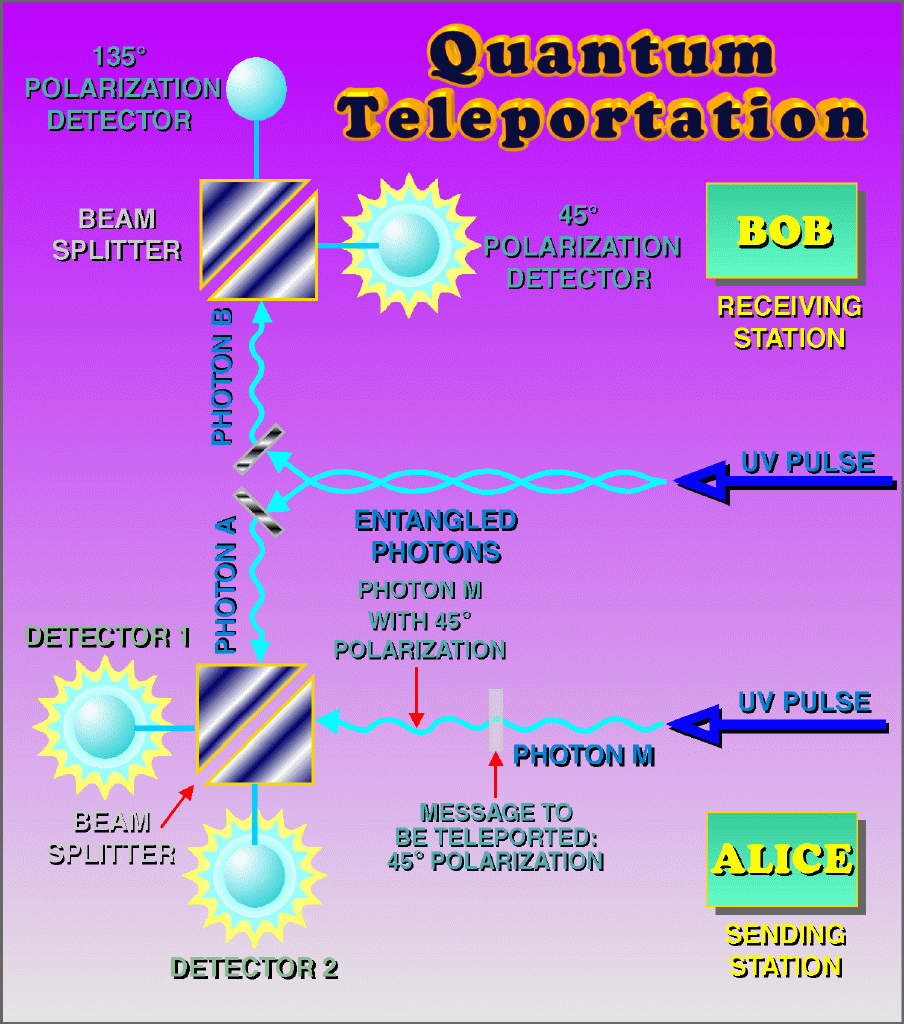 क्वांटम टेलीपोर्टेशन, जो अक्सर प्रकाश की तुलना में तेजी से यात्रा करने में भ्रमित होता है। वास्तव में, प्रकाश की गति की तुलना में जानकारी तेजी से प्रसारित नहीं होती है।
क्वांटम टेलीपोर्टेशन, जो अक्सर प्रकाश की तुलना में तेजी से यात्रा करने में भ्रमित होता है। वास्तव में, प्रकाश की गति की तुलना में जानकारी तेजी से प्रसारित नहीं होती है।लेकिन यह नहीं हो सकता! वास्तव में, कोई भी जानकारी प्रसारित नहीं होती है। एक स्थान पर एक कण को मापना और बहुत दूर स्थित कण में किसी चीज को संचारित करने के लिए इसका उपयोग करना असंभव है। कई सरल योजनाएं विकसित की गई हैं, यह कल्पना की गई है कि इस संपत्ति का उपयोग करते हुए, प्रकाश की तुलना में तेजी से जानकारी संचारित करें, लेकिन 1993 में उन्होंने साबित किया कि यह तंत्र जानकारी के प्रसारण की अनुमति नहीं देगा। इसके लिए एक सरल व्याख्या है:
• यदि आप "मेरे पास मौजूद कण की स्थिति क्या है" को मापते हैं, तो आपको दूसरे कण की स्थिति का पता चल जाएगा, लेकिन इस जानकारी के साथ तब तक कुछ नहीं किया जा सकता जब तक कि आप किसी अन्य कण तक नहीं पहुंचते या यह हम तक नहीं पहुंचता, और संदेश को जाना होगा प्रकाश या धीमी गति से।
• यदि आप अपने मौजूदा कण को एक निश्चित अवस्था में ले जाने के लिए मजबूर करते हैं, तो यह उलझे हुए कण की स्थिति को नहीं बदलेगा। इसके विपरीत, यह उलझाव को नष्ट कर देगा, ताकि आप दूसरे कण के बारे में कुछ भी न सीखें।
[
एथन ने समस्या के सार को पूरी तरह से प्रकट नहीं किया। यदि आप दस्ताने के साथ सादृश्य की कल्पना करते हैं तो उपरोक्त सभी आपको आश्चर्यचकित नहीं कर सकते हैं। किसी ने आपको एक जोड़ी से एक दस्ताने भेजा, और आपके दोस्त ने दूसरे को। और जब आप अपना पैकेज खोलते हैं, तो आप तुरंत पहचानते हैं कि न केवल कौन सा दस्ताने, बाएं या दाएं, आपको प्राप्त हुआ, बल्कि यह भी कि आपके दोस्त ने क्या प्राप्त किया। हालांकि, उलझे हुए कणों के मामले में, दस्ताने की स्थिति शुरू में निर्धारित नहीं होती है। और हम यह नहीं जानते हैं कि इसे कैसे निर्धारित किया जाए या क्या नहीं पता - यह वास्तव में यादृच्छिक रूप से निर्धारित किया गया है, और "दस्ताने" में से एक को मापने के क्षण में ठीक है। फिर दूसरे "दस्ताने" तुरंत विपरीत स्थिति मान लेते हैं। इसे आइंस्टीन ने "भयावह लंबी दूरी की कार्रवाई" / लगभग कहा है। ट्रांस। ]
 यदि दो कण उलझे हुए हैं, तो उनकी तरंग के गुण एक दूसरे के पूरक हैं, और उनमें से एक का माप दूसरे के गुणों को निर्धारित करता है। लेकिन क्या लहर फ़ंक्शन एक अमूर्त गणितीय विवरण है, या क्या यह ब्रह्मांड की गहरी सच्चाइयों और निर्णायक, मौलिक वास्तविकता को रेखांकित करता है, एक खुला प्रश्न है।
यदि दो कण उलझे हुए हैं, तो उनकी तरंग के गुण एक दूसरे के पूरक हैं, और उनमें से एक का माप दूसरे के गुणों को निर्धारित करता है। लेकिन क्या लहर फ़ंक्शन एक अमूर्त गणितीय विवरण है, या क्या यह ब्रह्मांड की गहरी सच्चाइयों और निर्णायक, मौलिक वास्तविकता को रेखांकित करता है, एक खुला प्रश्न है।यह यथार्थवादियों के लिए एक दार्शनिक समस्या है। इसका मतलब है कि एक कण की तरंग क्रिया - या कई कणों की उलझी हुई तरंग क्रिया - एक वास्तविक, भौतिक वस्तु है जो अस्तित्व में है और ब्रह्मांड में विकसित हो रही है, लेकिन इसके लिए बड़ी संख्या में असुविधाजनक धारणाओं की आवश्यकता होती है। यह माना जाना चाहिए कि संभावित वास्तविकताओं की एक अनंत संख्या है, और हम उनमें से केवल एक में रहते हैं, हालांकि दूसरों के अस्तित्व का कोई सबूत नहीं है। यदि आप एक साधनवादी हैं (लेखक के रूप में; यह सरल और अधिक व्यावहारिक है), तो आपको यह दार्शनिक समस्या नहीं है। आप बस इस बात का ध्यान रखें कि तरंग फ़ंक्शन गणनाओं का एक उपकरण है।
 आइंस्टीन क्वांटम यांत्रिकी के मामलों में एक वास्तविक यथार्थवादी थे, और उन्होंने इस पूर्वाग्रह को कब्र पर ले लिया। क्वांटम यांत्रिकी की उनकी व्याख्या का समर्थन करने के लिए कोई सबूत नहीं मिला, हालांकि उसके पास अभी भी कई अनुयायी हैं।
आइंस्टीन क्वांटम यांत्रिकी के मामलों में एक वास्तविक यथार्थवादी थे, और उन्होंने इस पूर्वाग्रह को कब्र पर ले लिया। क्वांटम यांत्रिकी की उनकी व्याख्या का समर्थन करने के लिए कोई सबूत नहीं मिला, हालांकि उसके पास अभी भी कई अनुयायी हैं।स्टीवन वेनबर्ग, एक नोबल पुरस्कार विजेता, स्टैंडर्ड मॉडल के सह-संस्थापक और कई क्षेत्रों में एक प्रतिभाशाली सैद्धांतिक भौतिक विज्ञानी, ने हाल ही में विज्ञान समाचार में इस तरह का वर्णन करते हुए साधनवाद के दृष्टिकोण की निंदा की:
यह कल्पना करना बहुत भयानक है कि हमारे पास मौजूद हर चीज के बारे में ज्ञान नहीं है - हम कह सकते हैं कि केवल माप लेने से क्या हुआ।
लेकिन आपके दार्शनिक विकास की परवाह किए बिना, क्वांटम यांत्रिकी काम करते हैं, और तरंग फ़ंक्शन, उलझाने वाले कण, आपको इस उलझाव को नष्ट करने की अनुमति देता है, यहां तक कि ब्रह्मांडीय दूरी पर भी। यह हमारे लिए ज्ञात ब्रह्मांड में एकमात्र त्वरित प्रक्रिया है, और इसलिए यह वास्तव में अलग है!
एथन सीगल - खगोल वैज्ञानिक, विज्ञान लोकप्रिय, एक बैंग्स के साथ शुरुआत के लेखक! उन्होंने "बियॉन्ड द गैलेक्सी" [ बियॉन्ड द गैलेक्सी ], और "ट्रैकनोलॉजी: स्टार ट्रेक का विज्ञान" [ ट्रेकोनोलॉजी ] किताबें लिखीं ।