🚂 🗯️ 🐁 हिग्स फील्ड कैसे काम करता है: 2) औसत गैर-शून्य पर हिग्स फ़ील्ड क्यों है 👨‍👧 👱🏿 🖨️

हिग्स फील्ड कैसे काम करता है:

यह कैसे होता है कि प्रकृति में हिग्स फ़ील्ड का औसत मूल्य शून्य नहीं है, जबकि प्रकृति के अन्य (स्पष्ट रूप से प्राथमिक) क्षेत्र जिन्हें हम जानते हैं कि शून्य है? [बहुत छोटा प्रिंट: अन्य क्षेत्र, निम्नतम स्तर के गुरुत्वाकर्षण क्षेत्र को छोड़कर, मीट्रिक कहलाते हैं, इससे आप अंतरिक्ष और समय के अस्तित्व को निर्धारित कर सकते हैं]।

सबसे पहले, फ़र्मियन फ़ील्ड में प्रकृति में एक बड़ा स्थिर नॉनज़रो मूल्य नहीं हो सकता है। यह फरमाइन्स और बोसोन के बीच अंतर के कारण है। बोसोन औसत नॉनजरो पर हो सकते हैं, लेकिन फ़र्मेशन नहीं कर सकते। तो आप न्यूट्रिनो और क्वार्क के बारे में इलेक्ट्रॉनों (और उनके चचेरे भाई म्यूओन्स और ताऊ) के बारे में भूल सकते हैं। छोटा प्रिंट: फ़र्मियन एक-दूसरे के साथ या एंटीफ़र्मेंस के साथ जोड़ सकते हैं और मिश्रित बोसॉन बना सकते हैं, जो औसत गैर-शून्य पर हो सकता है। यह ऊपरी और निचले क्वार्कों और उनके एंटीकार्क्स के लिए, और एक सुपरकंडक्टर में इलेक्ट्रॉनों के लिए ऐसा है। लेकिन यह एक लंबी कहानी है, और यह सीधे तौर पर हमारी चिंता नहीं करता है।

फोटॉन, ग्लून्स, डब्ल्यू और जेड के क्षेत्रों के बारे में क्या? ये सभी बोसोन हैं। सिद्धांत रूप में, इन क्षेत्रों में यूनिवर्स पर लगातार गैर-शून्य औसत मूल्य हो सकता है। लेकिन प्रयोगों, सिद्धांत नहीं, कहते हैं कि यह मामला नहीं है। विद्युत क्षेत्र का पर्याप्त रूप से बड़ा नॉनज़ेरो मूल्य विभिन्न प्रभावों की उपस्थिति का कारण होगा, जिसे हम निरीक्षण नहीं करते हैं। इनमें से सबसे महत्वपूर्ण बड़े पैमाने पर घूर्णी आक्रमण का उल्लंघन होगा। विद्युत क्षेत्र एक वेक्टर (स्पिन -1) है, यह एक निश्चित दिशा में इंगित करता है, इसलिए यदि यह नोनजरो है, तो यह मान जिस दिशा में इंगित करता है वह अन्य सभी से अलग होना चाहिए। (अंजीर। 1, नीचे बाएँ)।

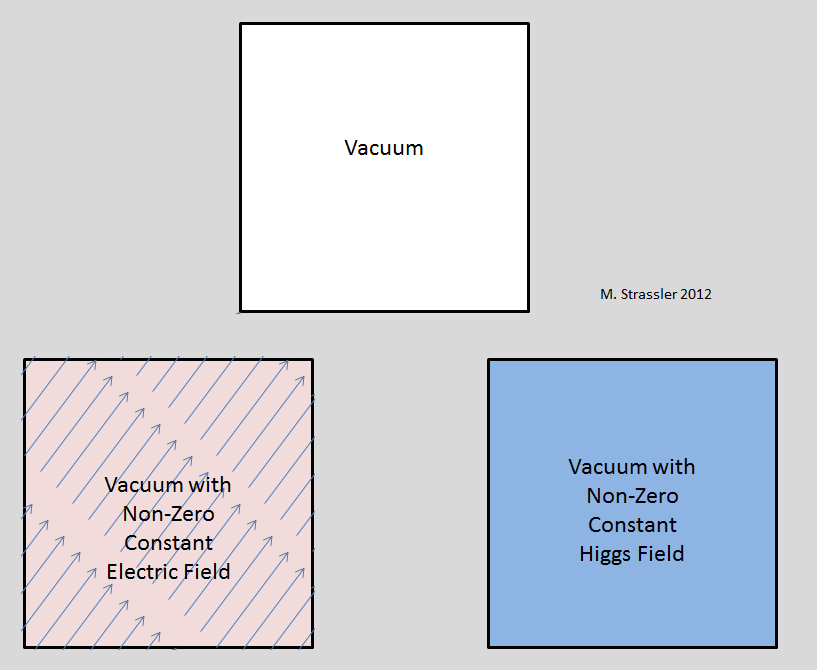अंजीर। 1

हिग्स फ़ील्ड स्केलर (स्पिन -0) है, यह कहीं भी इंगित नहीं करता है। अन्य अदिश क्षेत्रों में (न तो प्राथमिक और न ही सापेक्ष), हम वायु घनत्व क्षेत्र, पृथ्वी के अंदर दबाव क्षेत्र और समुद्र के तापमान का उदाहरण दे सकते हैं। अंतरिक्ष और समय के प्रत्येक बिंदु पर, घनत्व या दबाव या तापमान सिर्फ एक संख्या है, और विद्युत क्षेत्र एक संख्या और एक दिशा है। इसलिए यदि हिग्स क्षेत्र में एक गैर-अक्षीय मान है, तो कोई पसंदीदा दिशा नहीं है - अंजीर। 1, नीचे दाईं ओर। क्या अधिक अजीब है (चूंकि यह सापेक्ष है), हिग्स फ़ील्ड कोई पसंदीदा संदर्भ फ्रेम उत्पन्न नहीं करता है। वायु घनत्व के लिए, एक पसंदीदा संदर्भ प्रणाली है, क्योंकि आप या तो हवा के सापेक्ष आराम करते हैं या इसके माध्यम से आगे बढ़ते हैं। लेकिन हिग्स फील्ड के लिए ऐसा नहीं है; सभी पर्यवेक्षक उसके सापेक्ष आराम कर रहे हैं। इसलिए, आइंस्टीन के एसआरटी की सफलता, जो सभी प्रकार की घटनाओं का वर्णन करती है, गैर-मूल्य के एक सापेक्ष स्केलर क्षेत्र की उपस्थिति का विरोध नहीं करती है, जैसे कि हिग्स फ़ील्ड। संक्षेप में, एक गैर-शून्य हिग्स फ़ील्ड की उपस्थिति में, वैक्यूम ठीक उसी तरह व्यवहार करता है जैसे वह एच = 0 पर व्यवहार करेगा; इसकी उपस्थिति का पता कणों के द्रव्यमान पर प्रभाव (या कुछ और नाटकीय के माध्यम से, उदाहरण के लिए, एलएचसी का उपयोग हिग्स कण बनाने के लिए) के माध्यम से लगाया जा सकता है।

हिग्स क्षेत्र के लिए सबसे आसान तरीका पूरे ब्रह्मांड में एक गैर-शून्य मान बनाए रखना होगा यदि इसमें गैर-शून्य संतुलन मूल्य H ₀ अपनी कक्षा 1 गति समीकरण में भाग लेता है:

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = - (2 p i n u_{m i n})^{2} (H - H_{0})

$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - (2 \ pi \ nu_ {min}) ^ 2 (H - H_0)$

(यह कक्षा 1 होनी चाहिए, कक्षा 0 नहीं, ऐसे कारणों के लिए जो हिग्स कण पर चर्चा करने के बाद हमारे लिए स्पष्ट हो जाएंगे)। वास्तव में, स्थिति थोड़ी अधिक जटिल है। सही समीकरण इस तरह दिखेगा:

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = a^{2} H - b^{2} H^{3}

$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = a ^ 2 H - b ^ 2 H ^ 3$

जहाँ a और b स्थिरांक हैं (उनके वर्ग सकारात्मक हैं! ² H के सामने प्लस चिन्ह पर ध्यान दें और इसकी तुलना पिछले समीकरण में माइनस से करें), जिसके बारे में हम बाद में जानेंगे। इसे फिर से लिखा जा सकता है:

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = - b^{2} H (H^{2} - [a / b]^{2})

$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - [a / b] ^ 2)$

यदि स्थान और समय में H (x, t) एक स्थिर है, तो dH / dt = dH / dx = 0 है, इसलिए

0 = - b 2 H (H 2 - [a / b]^{2})

$0 = - b2 H (H2 - [a / b] ^ 2)$

(जब एच (एक्स, टी) एक्स और टी में एक स्थिर है), और उसके पास समाधान हैं (अभी के लिए, हम सब कुछ बहुत आसान कर देंगे:

1. एच = 0
2. एच = + ए / बी
3. एच = - ए / बी

दूसरे शब्दों में, संतुलन की स्थिति तीन हैं, एक नहीं। ठीक प्रिंट: मैं इसे यहाँ बहुत सरल करता हूं, लेकिन अर्थ के लिए पूर्वाग्रह के बिना।

यह तुरंत स्पष्ट नहीं है, लेकिन समाधान H = 0 अस्थिर है। स्थिति अंजीर में दिखाए गए फ़ॉर्म के कटोरे में गेंद की गति के समीकरण के समान है। 2 - एक शराब की बोतल के नीचे के समान। उनके तीन संतुलन स्थिति भी हैं, एक 0 पर और दो ± x _{0 पर} । लेकिन स्पष्ट रूप से 0 पर स्थिति अस्थिर है - कोई भी धक्का लाल गेंद को x = 0 से दूर रोल करने का कारण बनेगा, स्थिति में एक कार्डिनल परिवर्तन। इसके विपरीत, x = x ₀ पर संतुलन स्थिर है, क्योंकि कोई भी धक्का हरे रंग की गेंद को बिंदु x = x _{0 के} चारों ओर एक छोटे आयाम के साथ दोलन करने का कारण होगा - ऐसा कठोर परिवर्तन नहीं। वही x = -x ₀ पर एक हल्के हरे रंग की गेंद के लिए सही होगा। इसी तरह, हालांकि H = 0 हिग्स क्षेत्र के समीकरण का हल होगा, हमारे ब्रह्मांड का इतिहास इस बात के लिए जटिल है कि हिग्स फ़ील्ड को ठीक से किक किया जाए, इसलिए यह उस स्थिति में नहीं रह सकता है। इसके बजाय, हिग्स फ़ील्ड एक गैर-शून्य मान और एक स्थिर स्थिति में एक समाधान में था।

दशकों तक, प्रयोगों और सिद्धांत के संयोजन के लिए धन्यवाद, हम जानते थे कि हिग्स फील्ड (जिसे पारंपरिक रूप से "v" कहा जाता है) का मूल्य 246 GeV है। यह हमें उन स्थिरांक और बी का एक विचार देता है:

a = vb = (246 GeV) b

इस प्रकार, हम बी के माध्यम से निर्धारित कर सकते हैं, और हम हिग्स गति समीकरण को फिर से लिख सकते हैं:

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = - b^{2} H (H^{2} - v^{2})

$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - v ^ 2)$

लेकिन यह हमें स्वयं बी का विचार नहीं देता है। अगले लेख में हम उसके बारे में और जानेंगे।

अब, हालांकि मैंने सब कुछ तैयार कर लिया है ताकि एच वी या वी के बराबर हो सके, इससे कोई फर्क नहीं पड़ता कि हिग्स क्षेत्र सकारात्मक है या नकारात्मक (वास्तव में, और भी संभावनाएं हैं, नीचे देखें); दुनिया ठीक वैसी ही निकलेगी, उसी भौतिकी के साथ, क्योंकि H के संकेत पर कुछ भी निर्भर नहीं करता है। यह तुरंत स्पष्ट नहीं हो जाता है, लेकिन यह है; एक संकेत - जहाँ भी आप H को समीकरणों में वर्णित करते हैं या मैं वर्णन करता हूँ कि Higgs फ़ील्ड कैसे काम करता है, H ² हर जगह दिखाई देता है, और न केवल H - और H ² H = v या H = -v पर निर्भर नहीं करता है । [छोटा प्रिंट: वास्तव में, एच एक जटिल क्षेत्र है, वास्तविक और काल्पनिक भागों के साथ, इसलिए एच किसी भी जटिल संख्या z के बराबर हो सकता है जिसके लिए z | z | = 1 | और वास्तव में, एच * एच = | एच | ² , लेकिन यह z पर निर्भर नहीं करता है। और यहां तक कि यह सब नहीं है! लेकिन आज के लिए पर्याप्त है।]

यदि आप एक रास्ता (उदाहरण के लिए, लार्ज हैड्रॉन कोलाइडर में एक दूसरे के साथ प्रोटॉन को टकराकर) पाते हैं, तो हिग्स फ़ील्ड में गड़बड़ी को धक्का देने या पेश करने के लिए, यह दोलन करेगा और इसे - यानी, लहरें इसमें दिखाई देती हैं

H = v + A c o s [2 p i (n u t - x / l a m b d a)]

$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$

जहां A तरंग आयाम है, ν और λ आवृत्ति और तरंग दैर्ध्य है, और ν और λ के बीच संबंध गति के समीकरण के सटीक रूप पर निर्भर करता है, विशेष रूप से, b और v पर। चूंकि हिग्स फ़ील्ड क्वांटम है, इसलिए इन तरंगों का आयाम निर्धारित किया जाएगा, और इन तरंगों की मात्रा को हम हिग्स कण कहते हैं। अगली बार हम इन कणों के गुणों पर विचार करेंगे।

हिग्स फील्ड कैसे काम करता है: 2) औसत गैर-शून्य पर हिग्स फ़ील्ड क्यों है

More articles: