पुस्तक "क्वांटम यांत्रिकी। सैद्धांतिक न्यूनतम "

शास्त्रीय यांत्रिकी सहज है: यह जीवित रहने के लिए लोगों द्वारा दैनिक और बार-बार उपयोग किया जाता है। लेकिन बीसवीं शताब्दी तक, किसी ने भी क्वांटम यांत्रिकी का उपयोग नहीं किया था। वह इतनी छोटी चीजों का वर्णन करती है कि वे पूरी तरह से मानव इंद्रियों की धारणा से बाहर हो जाते हैं। इस सिद्धांत को समझने का एकमात्र तरीका, इसकी सुंदरता का आनंद लेने के लिए, अमूर्त गणित के साथ हमारे अंतर्ज्ञान को अवरुद्ध करना है।

लियोनार्ड Sasskind - एक प्रसिद्ध अमेरिकी वैज्ञानिक - आप क्वांटम यांत्रिकी के देश के लिए एक रोमांचक यात्रा पर जाने के लिए आमंत्रित करता है। रास्ते में, आपको स्कूल भौतिकी पाठ्यक्रम से बुनियादी ज्ञान की आवश्यकता होगी, साथ ही गणितीय विश्लेषण और रैखिक बीजगणित की मूल बातें भी। आपको उन मुद्दों के बारे में भी कुछ जानने की जरूरत है, जो "सैद्धांतिक न्यूनतम" की पहली पुस्तक में सस्कुइंड को संबोधित किया गया था - "आधुनिक भौतिकी के बारे में आपको जो कुछ भी जानना आवश्यक है।" लेकिन यह निडर है अगर यह ज्ञान कुछ हद तक भूल जाता है। बहुत से लेखक रास्ते भर याद दिलाएंगे और समझाएंगे।

क्वांटम यांत्रिकी एक असामान्य सिद्धांत है: इसके पोस्टुलेट्स के अनुसार, उदाहरण के लिए, हम सिस्टम के बारे में सब कुछ जान सकते हैं और इसके व्यक्तिगत भागों के बारे में कुछ नहीं। आइंस्टीन और नील्स बोह्र ने इस और अन्य विरोधाभासों के बारे में बहुत तर्क दिया। यदि आप कठिनाइयों से डरते नहीं हैं, एक जिज्ञासु मन है, तो तकनीकी रूप से सक्षम हैं, ईमानदारी से और गहराई से भौतिकी में रुचि रखते हैं, तो लियोनार्ड सस्किंड के व्याख्यान का यह पाठ्यक्रम आपको अपील करेगा। पुस्तक क्वांटम सिद्धांत के तार्किक सिद्धांतों पर केंद्रित है और इसका उद्देश्य क्वांटम तर्क के विरोधाभास को चिकना करना नहीं है, बल्कि इसे दिन की रोशनी में खींचना है और कठिन मुद्दों से निपटने की कोशिश करना है जो इसे उठाता है।

वेव फंक्शन ओवरव्यू

इस व्याख्यान में हम लहर कार्यों की भाषा का उपयोग करेंगे, तो आइए गोता लगाने से पहले सामग्री की एक छोटी समीक्षा करें। हमने व्याख्यान 5 में अमूर्त वस्तुओं के तरंग कार्यों पर चर्चा की, यह बताए बिना कि वे तरंगों या कार्यों से कैसे संबंधित हैं। इस अंतर को भरने से पहले, मैं आपको याद दिलाता हूं कि हमने पहले क्या चर्चा की थी।

के साथ शुरू करने के लिए, हम eigenvalues ​​l और eigenvectors के साथ एक अवलोकन योग्य L चुनते हैं। l choose चलो | Y〉 एक राज्य वेक्टर है। चूंकि हर्मिटियन ऑपरेटर के eigenvectors एक पूर्ण ऑर्थोनॉमिक आधार बनाते हैं, वेक्टर | Y〉 को इस में विस्तारित किया जा सकता है:

जैसा कि आप अनुभाग 5.1.2 और 5.1.3 से याद करते हैं, मात्रा Y (l) को सिस्टम का तरंग फ़ंक्शन कहा जाता है। लेकिन ध्यान दें: वाई (एल) का विशिष्ट रूप उस विशिष्ट अवलोकन एल पर निर्भर करता है जिसे हमने मूल रूप से चुना था। यदि हम एक और अवलोकनीय चुनते हैं, तो तरंग फ़ंक्शन (आधार वैक्टर और आइगेनवेल्यूज़ के साथ) अलग हो जाएंगे, इस तथ्य के बावजूद कि हम अभी भी एक ही राज्य के बारे में बात कर रहे हैं। इसलिए, हमें एक आरक्षण करना चाहिए कि Y (l) तरंग से संबंधित है। Yñ सटीक होने के लिए, हमें यह कहना होगा कि Y- (L) L- आधार में तरंग फ़ंक्शन है। यदि हम वैक्टर के इस आधार के orthonormality गुणों का उपयोग करते हैं l li | lj〉 = dij, तो इस L- आधार में तरंग फ़ंक्शन को राज्य वेक्टर के आंतरिक उत्पादों (या अनुमानों) का उपयोग करके भी परिभाषित किया जा सकता है। eigenvectors पर Y | l〉: Y (l) ) = | एल | वाई 〈

तरंग फ़ंक्शन के बारे में सोचने के दो तरीके हैं। सबसे पहले, यह एक विशिष्ट आधार में राज्य वेक्टर के घटकों का एक सेट है। इन घटकों को स्तंभ वेक्टर के रूप में लिखा जा सकता है:



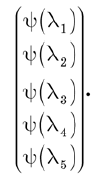
लहर फ़ंक्शन के बारे में सोचने का एक और तरीका यह है कि इसे एल के फ़ंक्शन के रूप में माना जाए। यदि आप l का कोई मान्य मान सेट करते हैं, तो फ़ंक्शन Y (l) एक जटिल संख्या देता है। इस प्रकार, हम कह सकते हैं कि वाई (एल) असतत चर एल का एक जटिल-मूल्यवान फ़ंक्शन है। इस विचार के साथ, रैखिक ऑपरेटर ऑपरेशन बन जाते हैं जो कार्यों पर लागू होते हैं और नए कार्य देते हैं।

और एक और अंतिम अनुस्मारक: संभावना है कि प्रयोग परिणाम देगा एल पी (एल) = वाई * (एल) वाई (एल) के बराबर है।

कार्य और क्षेत्र

अब तक, हमने जिन प्रणालियों का अध्ययन किया था उनमें परिमित आयामी वैक्टर थे। उदाहरण के लिए, एक साधारण स्पिन का वर्णन द्वि-आयामी राज्य स्थान द्वारा किया जाता है। इस कारण से, वेधशालाओं में केवल संभावित अवलोकन मूल्यों की सीमित संख्या थी। लेकिन अधिक जटिल वेधशालाएं हैं जिनमें अनंत मान हो सकते हैं। एक उदाहरण एक कण है। कण निर्देशांक अवलोकनीय हैं, लेकिन स्पिन के विपरीत, निर्देशांक में अनंत मान संभव हैं। उदाहरण के लिए, x अक्ष के साथ एक कण किसी भी भौतिक चिह्न x पर हो सकता है। दूसरे शब्दों में, x एक सतत अनंत चर है। जब मनाया सिस्टम निरंतर होता है, तो तरंग फ़ंक्शन निरंतर चर का एक पूर्ण विकसित फ़ंक्शन बन जाता है। इस तरह की प्रणालियों के लिए क्वांटम यांत्रिकी लागू करने के लिए, हमें वैक्टर की अवधारणा का विस्तार करना चाहिए ताकि इसमें कार्यों को शामिल किया जा सके।

कार्य कार्य हैं, और वैक्टर वैक्टर हैं; वे पूरी तरह से अलग-अलग संस्थाएं प्रतीत होते हैं, इसलिए फंक्शन वैक्टर किस अर्थ में हैं? यदि आप वैक्टर को तीन-आयामी अंतरिक्ष में तीर के रूप में सोचते हैं, तो निश्चित रूप से वे सभी कार्यों के समान नहीं हैं। लेकिन अगर आप वैक्टरों को अधिक व्यापक रूप से देखते हैं, जैसा कि गणितीय वस्तुओं में कुछ पदों को संतुष्ट करता है, तो फ़ंक्शन वास्तव में एक वेक्टर स्थान बनाते हैं। ऐसे वेक्टर स्थान को अक्सर गणितज्ञ डेविड हिल्बर्ट के सम्मान में हिल्बर्ट स्पेस कहा जाता है।

एक वास्तविक चर x के जटिल कार्यों Y (x) के सेट पर विचार करें। एक जटिल फ़ंक्शन द्वारा, मेरा मतलब है कि प्रत्येक x के लिए यह एक जटिल संख्या Y (x) को जोड़ता है। दूसरी ओर स्वतंत्र चर x, एक साधारण वास्तविक चर है। यह किसी भी वास्तविक मूल्यों को ∞∞ से + values ​​तक ले जा सकता है।

अब हम कहते हैं कि हमारे कहने का अर्थ है कि "कार्य वैक्टर हैं"। यह एक सतही उपमा या रूपक नहीं है। कुछ प्रतिबंधों के तहत (जो हम बाद में वापस आएंगे), वाई (एक्स) जैसे कार्य गणितीय स्वयंसिद्ध को संतुष्ट करते हैं जो एक वेक्टर स्थान को परिभाषित करते हैं। हमने इस विचार का खंड 1.9.2 में उल्लेख किया है, और अब हम इसका उपयोग पूरी ताकत से करते हैं। एक जटिल वेक्टर अंतरिक्ष के axioms (धारा 1.9.1 में) को देखते हुए, हम देखते हैं कि जटिल कार्य उन सभी को संतुष्ट करते हैं।

1. किन्हीं दो कार्यों का योग एक फंक्शन है।
2. कार्यों को जोड़ना सराहनीय है।
3. कार्यों का जोड़ साहचर्य है।
4. एक अनोखा शून्य फ़ंक्शन है जैसे कि जब इसे किसी फ़ंक्शन में जोड़ा जाता है, तो समान फ़ंक्शन प्राप्त होता है।
5. किसी दिए गए फ़ंक्शन Y (x) के लिए, एक विशिष्ट फ़ंक्शन है-Y (x) जैसे कि Y (x) + (-Y (x)) = 0।
6. किसी भी जटिल संख्या द्वारा एक फ़ंक्शन का गुणन एक फ़ंक्शन देता है और रैखिक होता है।
7. वितरण संपत्ति देखी जाती है, जिसका अर्थ है कि

z [y (x) + j (x)] = zY (x) + zj (x),
[z + w] Y (x) = zY (x) + wY (x),

जहाँ z और w जटिल संख्या हैं।

इसका तात्पर्य यह है कि हम ket वेक्टर के साथ Y (x) फ़ंक्शन की पहचान कर सकते हैं। सार वेक्टर स्पेस में Y we। यह आश्चर्य की बात नहीं है कि हम ब्रा-वैक्टर को भी परिभाषित कर सकते हैं। ब्रा-वेक्टर | Y | चूम साल के अनुरूप। Y identified की पहचान जटिल संयुग्मन क्रिया Y * (x) से की जाती है।

इस विचार का प्रभावी ढंग से उपयोग करने के लिए, हमें अपने गणितीय उपकरणों के सेट से कुछ वस्तुओं को सामान्य बनाने की आवश्यकता है। पिछले व्याख्यानों में, तरंगों की पहचान करने वाले लेबल कुछ परिमित असतत सेट के सदस्य थे, उदाहरण के लिए, एक निश्चित अवलोकन के स्वदेशी। लेकिन अब स्वतंत्र चर निरंतर है। अन्य बातों के अलावा, इसका मतलब है कि हम इसे साधारण राशियों का उपयोग करके सारांशित नहीं कर सकते हैं। मुझे लगता है कि आप जानते हैं कि क्या करना है। यहां हमारी तीन वेक्टर अवधारणाओं के लिए फ़ंक्शन-उन्मुख विकल्प हैं, जिनमें से दो आप पहले से ही परिचित हैं।

• अभिन्नों को प्रतिस्थापित किया जाता है।
• संभावनाओं को संभावना घनत्व द्वारा प्रतिस्थापित किया जाता है।
• क्रोनकर डेल्टा प्रतीक को डीरेका डेल्टा फ़ंक्शन द्वारा बदल दिया गया है।

आइए इन उपकरणों पर करीब से नज़र डालें।

अभिन्नों द्वारा प्रतिस्थापित किया जाता है । यदि हम वास्तव में कठोरता बनाए रखना चाहते हैं, तो हम एक्स अक्ष को बदलने के लिए बहुत छोटे अंतराल द्वारा अलग किए गए बिंदुओं के असतत सेट के साथ शुरू करेंगे small, और फिर सीमा पर आगे बढ़ें 0. → 0. यह प्रत्येक चरण को सही ठहराने के लिए कई पृष्ठ लेगा। लेकिन हम कुछ सहज परिभाषाओं के साथ इस परेशानी से बच सकते हैं, जैसे कि इंटीग्रल्स के साथ रकम बदलना। योजनाबद्ध रूप से, इस दृष्टिकोण को निम्नानुसार लिखा जा सकता है:



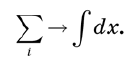
उदाहरण के लिए, यदि आपको वक्र के नीचे के क्षेत्र की गणना करने की आवश्यकता है, तो एक्स अक्ष को छोटे सेगमेंट में विभाजित किया गया है, फिर एक बड़ी संख्या में आयतों के क्षेत्रों को एक प्राथमिक गणितीय विश्लेषण की तरह जोड़ा जाता है। जब हम सेगमेंट को शून्य आकार का करार देते हैं, तो योग एक अभिन्न अंग बन जाता है।

कंस पर गौर कीजिए | Y | और ket | Y〉 और उनके आंतरिक उत्पाद को परिभाषित करें। ऐसा करने का स्पष्ट तरीका एकीकरण में समीकरण (1.2) के साथ एकीकरण को बदलना है। हम आंतरिक उत्पाद को निम्नानुसार परिभाषित करते हैं:



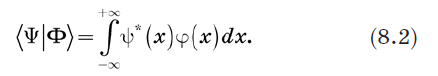संभावनाओं को संभावना घनत्व द्वारा प्रतिस्थापित किया जाता है । अगला, हम चर x के लिए संभाव्यता घनत्व के साथ P (x) = Y * (x) Y (x) की पहचान करते हैं। प्रायिकता घनत्व के साथ क्यों, और न केवल संभाव्यता के साथ? यदि x एक सतत चर है, तो संभावना है कि यह किसी भी बिल्कुल दिए गए मूल्य को ले जाएगा, आमतौर पर शून्य है। इसलिए, प्रश्न को इस तरह से प्रस्तुत करना अधिक सही है: क्या संभावना है कि x दो मानों के बीच है x = a और x = b? संभावना घनत्व निर्धारित किया जाता है ताकि यह संभावना अभिन्न द्वारा दी गई हो



चूंकि कुल संभावना 1 होनी चाहिए, इसलिए हम वेक्टर के सामान्यीकरण को परिभाषित कर सकते हैं



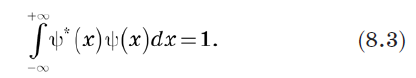क्रोनकर डेल्टा प्रतीक को डीरेका डेल्टा फ़ंक्शन द्वारा बदल दिया गया है । अब तक, सब कुछ बहुत परिचित है। डिराक डेल्टा समारोह कुछ नया है। डेल्टा फ़ंक्शन, क्रोनकर डेल्टा प्रतीक dij का एक एनालॉग है, जो कि परिभाषा में 0 है अगर मैं if j, और 1 if i = j है। लेकिन इसे दूसरे तरीके से परिभाषित किया जा सकता है। एक परिमित आयामी अंतरिक्ष में किसी भी वेक्टर फाई पर विचार करें। यह देखना आसान है कि क्रोनकर डेल्टा प्रतीक स्थिति को संतुष्ट करता है



यह इस तथ्य के कारण है कि इस राशि में केवल j = i नॉनज़रो है। सारांश के दौरान, क्रोनकर प्रतीक एफ को छोड़कर एफ के सभी घटकों को फ़िल्टर करता है। इसका एक स्पष्ट सामान्यीकरण एक नए फ़ंक्शन को परिभाषित करना होगा जिसमें इंटीग्रल के तहत उपयोग किए जाने पर समान फ़िल्टरिंग गुण होता है। दूसरे शब्दों में, हमें एक नई इकाई d (x - x ') की आवश्यकता है, जिसमें वह गुण है जो किसी भी फ़ंक्शन F (x) के लिए है



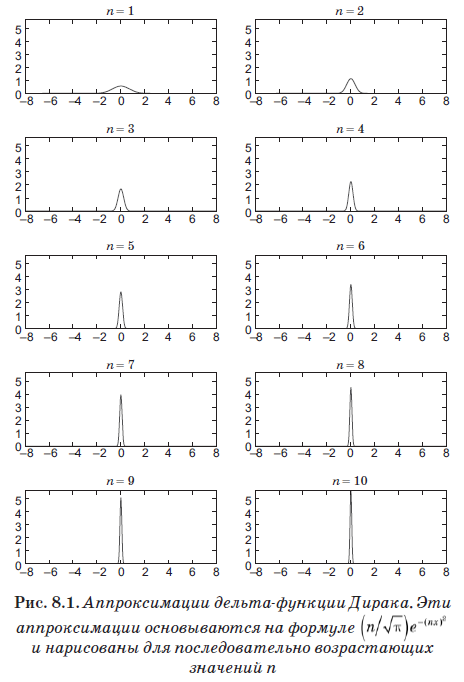
समीकरण (8.4) डिराक डेल्टा फ़ंक्शन नामक एक नई इकाई को परिभाषित करता है, जो क्वांटम यांत्रिकी में सबसे महत्वपूर्ण उपकरण निकला। लेकिन इसके नाम के बावजूद, यह वास्तव में सामान्य अर्थों में एक फ़ंक्शन नहीं है। यह शून्य के बराबर है जहां x 'x ’है, लेकिन जब x = x’ यह अनंत तक जाता है। वास्तव में, यह सिर्फ इतना अनंत है कि d (x) के तहत क्षेत्र 1 के बराबर है। मोटे तौर पर, यह फ़ंक्शन असीम रूप से छोटे अंतराल ε पर नॉनज़रो है, लेकिन इस अंतराल पर इसका मान 1 / inf है। इस प्रकार, इसके तहत क्षेत्र 1 के बराबर है, और, अधिक महत्वपूर्ण बात, यह समीकरण (8.4) को संतुष्ट करता है। समारोह



n के बहुत बड़े मूल्यों के लिए डेल्टा फ़ंक्शन को काफी अच्छी तरह से अनुमानित करता है। अंजीर में। 8.1 n के बढ़ते मूल्यों के साथ इस अनुकूलन को दर्शाता है। इस तथ्य के बावजूद कि हम n = 10 पर बस गए, अर्थात, बहुत कम मूल्य, ध्यान दें कि ग्राफ पहले से ही बहुत संकीर्ण और तेज चोटी बन गया है।



»पुस्तक की अधिक जानकारी प्रकाशक की वेबसाइट पर पाई जा सकती है
» सामग्री
» अंश

इस ब्लॉग के पाठकों के लिए, कूपन पर 20% की छूट - Sasskind