सूर्य के डिस्क पर शुक्र के पारित होने और उनके बीच की दूरी का निर्धारण

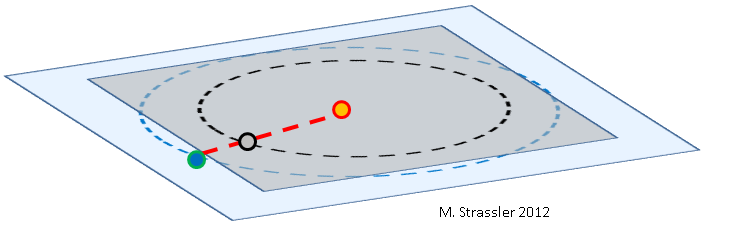
अंजीर। 1: पृथ्वी (नीला), शुक्र (ग्रे), और सूर्य (नारंगी), पैमाने पर नहीं।

2012 में सूर्य की डिस्क के माध्यम से शुक्र के पारित होने के बारे में, कई लेख पहले ही लिखे जा चुके हैं। यह घटना कितनी दुर्लभ है, और क्यों ठीक है: सिद्धांत रूप में, शुक्र, पृथ्वी की तुलना में सूर्य के चारों ओर अधिक बार घूम रहा है, पृथ्वी और सूर्य के बीच अपने प्रत्येक मोड़ (छवि 1) के दौरान गुजरना चाहिए, लेकिन क्योंकि। दो ग्रहों की कक्षाओं को संरेखित नहीं किया गया है (वे एक ही विमान में नहीं हैं, चित्र 2 देखें), शुक्र अक्सर पृथ्वी के दृष्टिकोण से सूर्य के ऊपर या नीचे से गुजरता है।

लेकिन दूसरों के शब्दों को दोहराने के बजाय, मैं कुछ विवरण जोड़ना चाहता हूं जो इंटरनेट पर ढूंढना इतना आसान नहीं है।

आपने पढ़ा होगा कि खगोलविज्ञानी एडमंड हैली (प्रसिद्ध धूमकेतु हैली) के तर्क के आधार पर एक तकनीक का उपयोग करते हुए उनके द्वारा 1678 से 1716 तक, साथ ही साथ जेम्स ग्रेगरी ने, 1716 में शुक्र के पारित होने का उपयोग पृथ्वी से पृथ्वी की दूरी निर्धारित करने के लिए किया था। 2% की त्रुटि के साथ सूर्य (और शुक्र से पहले, और अन्य सभी ग्रह) उस समय प्राप्त किए गए उच्चतम हैं। यह आशा की गई थी कि सटीकता 10 गुना अधिक होगी, लेकिन " ब्लैक ड्रॉप इफेक्ट " नामक एक अप्रत्याशित ऑप्टिकल प्रभाव इस प्रक्रिया में हस्तक्षेप करता है - इसके होने के सटीक कारणों के बारे में अभी भी बहस चल रही है। लेकिन आपने यह नहीं पढ़ा होगा कि यह माप - और खगोल विज्ञान में दूरियों के कई अन्य माप, काफी करीबी सितारों तक - लंबन के सिद्धांत पर आधारित है, एक ही ज्यामितीय तथ्य पर कि हमारी आँखें और मस्तिष्क गहराई का अनुभव करने के लिए उपयोग करते हैं, या हमारी महसूस करने की क्षमता कितनी दूर की वस्तुएं बस हमें देख रही हैं।


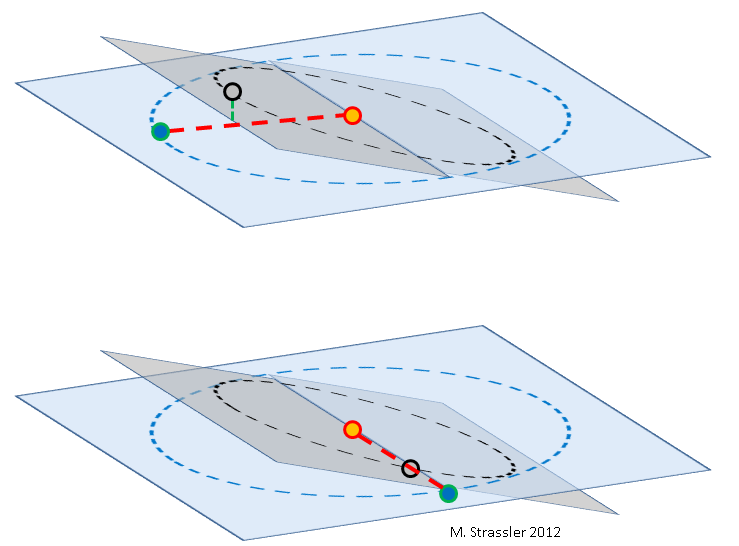अंजीर। 2: पृथ्वी (नीला), शुक्र (धूसर) और सूर्य (नारंगी), पैमाने पर नहीं। शुक्र की कक्षा (एक ग्रे आयत में एक काला वृत्त) पृथ्वी की कक्षा (एक नीले आयत में एक नीला वृत्त) के सापेक्ष झुका हुआ है। झुकाव की डिग्री बहुत अतिरंजित है। चूंकि पृथ्वी और शुक्र अलग-अलग गति से सूर्य की परिक्रमा करते हैं, वे कक्षाओं में किसी भी बिंदु पर एक दूसरे को पारित कर सकते हैं।

शीर्ष: इस मार्ग के दौरान, शुक्र पृथ्वी या सूर्य (लाल रेखा) को जोड़ने वाली रेखा के ऊपर या नीचे (ग्रीन लाइन) स्थित होता है, इसलिए शुक्र सौर डिस्क से नहीं गुजरता है।

नीचे: दुर्लभ मामलों में, पृथ्वी और सूर्य को जोड़ने वाली रेखा कक्षाओं के विमानों के चौराहे की रेखा से मेल खाती है, और शुक्र उसी रेखा के पास है, जो मार्ग की ओर जाता है।

लंबन के बिना, शुक्र से सूर्य की सापेक्ष दूरी को निर्धारित करना भी आसान है - अर्थात, पृथ्वी की कक्षा एल _ई की त्रिज्या के लिए शुक्र एल _वी की कक्षा की त्रिज्या का अनुपात _। इसलिए, पुनर्जागरण के खगोल विज्ञान में, ग्रहों से पृथ्वी और सूर्य की सापेक्ष दूरी की गणना काफी पहले की गई थी। लेकिन एल _वी और एल _{ई को} अलग-अलग निर्धारित करने के लिए, लंबन को मापना आवश्यक है, और शुक्र का मार्ग इसे प्रदान कर सकता है। 1760 के दशक में शुक्र के पारित होने ने L _E - L _V की काफी सटीक माप की, पृथ्वी से शुक्र की "पूर्ण" दूरी; इसने एल _ई , एल _वी , और कुछ प्रतिशत की त्रुटि के साथ अन्य सभी ग्रहों की दूरियों का पता लगाना संभव बना दिया। इससे पहले, 17 वीं शताब्दी के अंत में, पृथ्वी से मंगल तक की दूरी का एक माप किया गया था, जिसमें लगभग 10% की त्रुटि थी; यह भी लंबन पर आधारित था, लेकिन यह एक पूरी तरह से अलग कहानी है।

प्रारंभिक टिप्पणी: पृथ्वी और शुक्र, और यहां तक ​​कि सूर्य भी उनके बीच की दूरी की तुलना में बहुत छोटा है, इसलिए उनकी छवियों को खींचना लगभग असंभव है। दृष्टांतों में, आपको हमेशा उन ग्रहों से बड़ा बनाना होगा, जो वास्तव में उनके बीच की दूरियों के संबंध में हों, ताकि आप अवधारणा को समझ सकें। इसे ध्यान में रखें! मेरे सभी दृष्टांत पैमाने पर नहीं आते।

शुक्र और पृथ्वी की कक्षाओं के सापेक्ष आकार

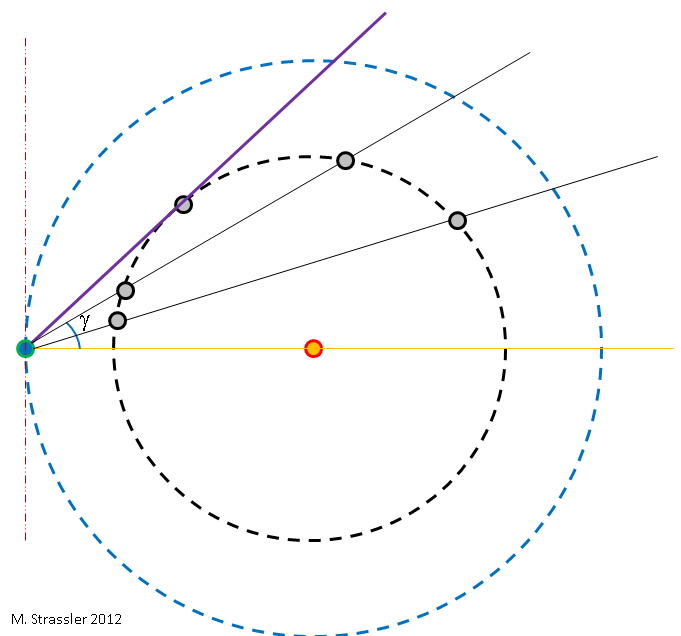
अंजीर। 3

एल _वी / एल _ई के निर्धारण की सादगी का मुख्य कारण समझने के लिए, मान लीजिए कि पृथ्वी और शुक्र की कक्षाएं गोलाकार और संरेखित हैं - वे एक ही विमान में झूठ बोलते हैं (जैसा कि चित्र 1, आइसोमेट्रिक और चित्र 3 में दिखाया गया है) एक "शीर्ष दृश्य" है)। वास्तव में, पृथ्वी और शुक्र की कक्षाएँ थोड़ी लम्बी हैं और संरेखित नहीं हैं (चित्र 2)। लेकिन विमानों की अण्डाकारता और बेमेलता हमारे तर्क के लिए बहुत महत्वपूर्ण नहीं है, इसलिए पहले हम उन्हें अनदेखा कर सकते हैं, और फिर अधिक सटीक उत्तर पाने के लिए फिर से याद कर सकते हैं।

यहां हम भौतिकी के लिए प्रौद्योगिकी को शास्त्रीय रूप से लागू करेंगे: हम वर्तमान कार्य के लिए पर्याप्त सन्निकटन करेंगे और हम आवश्यकता से अधिक गहराई तक नहीं जाएंगे। यह सामान्य रूप से विज्ञान और ज्ञान के बारे में सोचने का एक बहुत शक्तिशाली तरीका है - यह किसी भी स्तर की सटीकता के साथ किसी भी प्रश्न का उत्तर देने के लिए पर्याप्त है, इसलिए आप उन सरलतम तकनीकों का उपयोग कर सकते हैं जो आपको सटीकता का वांछित स्तर प्रदान करेंगे। इस पद्धति का सदियों से पूरी तरह से उपयोग किया गया है और यह न केवल भौतिकी के लिए लागू है।

इसलिए, हम अनुमान लगा लेंगे जिसमें कक्षाएं गोलाकार और संरेखित हैं, और हमें कुछ प्रतिशत की त्रुटि के साथ लगभग सही उत्तर प्राप्त होंगे। यह मूल अवधारणाओं को प्रदर्शित करने के लिए पर्याप्त होगा, जो मैं चाहता हूं। मेरा विश्वास करो, आप बहुत अधिक सटीक गणना कर सकते हैं - या आप खुद इस मामले में एक विशेषज्ञ बन सकते हैं। लेकिन हमारा अनुमान न केवल बहुत अच्छा उत्तर देगा, बल्कि यह भी दिखाएगा कि एल _वी के एल एल के अनुपात की गणना करना इतना आसान क्यों है, लेकिन एल _वी और एल _ई के मूल्यों को स्वयं नहीं।

उस वर्ष के दौरान जब पृथ्वी और शुक्र अलग-अलग गति से सूर्य की परिक्रमा करते हैं, सूर्य के संबंध में पृथ्वी और शुक्र की सापेक्ष स्थिति बदलती है। यदि एक निश्चित दिन (दिन, महीने, साल) पर मैं केंद्र में सूर्य के साथ और बाईं ओर पृथ्वी के साथ एक चित्र बनाने का फैसला करता हूं, जैसा कि अंजीर में है। 2, तब शुक्र अपनी कक्षा में कहीं भी हो सकता है। इसका मतलब यह है कि पृथ्वी के दृष्टिकोण से, शुक्र और आकाश में सूर्य के बीच का कोण तारीख के आधार पर बदल जाएगा। यह अंजीर में दिखाया गया है। 3, जहां कोण को is कहा जाता है। कोण को मापना आसान है; सूर्यास्त के बाद या सूर्योदय से पहले आसमान में शुक्र को खोजें और शुक्र और सूर्य के बीच के कोण को मापें; तस्वीर देखें 4।


अंजीर। 4

अंजीर से। चित्रा 3 से पता चलता है कि 3 का अधिकतम आकार है - नारंगी और बैंगनी रेखाओं के बीच का कोण। कक्षा में घूमते हुए, शुक्र प्रत्येक सूर्यास्त के साथ कहीं और दिखाई देगा; कुछ समय के लिए यह एक पंक्ति में कई रातों तक क्षितिज से ऊपर उठ जाएगा, और फिर धीरे-धीरे नीचे दिखाई देने लगेगा। एक पंक्ति में कई रातों के लिए शुक्र को देखना और we को मापना, हम अधिकतम मूल्य का निर्धारण कर सकते हैं, जिसे मैं several _{अधिकतम} कहूंगा।

अंजीर से। 3 यह स्पष्ट है कि (जैसा कि अंजीर में दिखाया गया है। 4) less _{अधिकतम} 90 ° से कम है, क्योंकि बैंगनी रेखा नारंगी और लाल, लंबवत के बीच होनी चाहिए। ज्यामितीय रूप से, यह इस तथ्य का परिणाम है कि शुक्र हमेशा पृथ्वी की तुलना में सूर्य के अधिक निकट होता है। ये कोण समझाते हैं कि शुक्र हमेशा सूर्यास्त के तुरंत बाद या भोर से पहले क्यों दिखाई देता है (उन दिनों को छोड़कर जब यह सूर्य के पीछे स्थित होता है)। वीनस अंधेरे के बाद अपने चरम पर नहीं हो सकता है, क्योंकि इसके लिए उसे लाल रेखा के बाईं ओर रहना होगा।


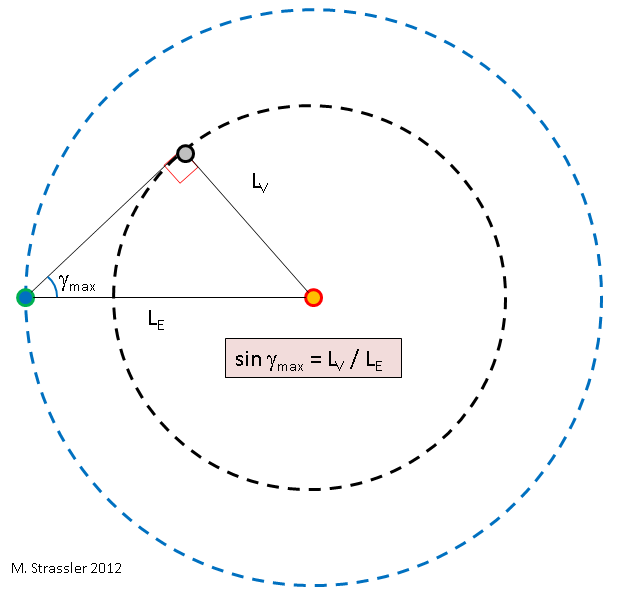
अंजीर। 5

अब हम - _{मैक्स} का उपयोग करके दो कक्षाओं - L _V से L _E की त्रिज्या के अनुपात को निर्धारित कर सकते हैं। यह सबसे सरल ज्यामिति है, अंजीर देखें। 5. निचली रेखा यह है कि जब शुक्र सूर्य से अधिकतम कोण पर होता है, तो सूर्य और शुक्र के बीच की रेखा पृथ्वी और शुक्र के बीच की रेखा के लंबवत होती है, इसलिए इन तीनों वस्तुओं को जोड़ने वाली रेखाएं एक सही त्रिकोण बनाती हैं। यहाँ से हम मानक त्रिकोणमिति का उपयोग करते हैं:

$$

$$L_V / L_E = \ gamma_ {max}$$

और यहाँ से, अन्य सरल ज्यामितीय सूत्रों की सहायता से, हम दूरियों के बीच अन्य ग्रहों के बीच संबंध प्राप्त करते हैं।

शुरुआत में संकेत दिए गए कारणों के लिए यह पूरी तरह से सही नहीं है; ग्रहों की कक्षाएँ दीर्घवृत्त हैं, और जल तल पर नहीं हैं। दूसरे शब्दों में, L _V और L _{E को} वर्ष के दौरान संग्रहीत नहीं किया जाता है, और applied _{अधिकतम} अंजीर में तीन आयामों में, थोड़ा और अधिक जटिल लगाया जाता है। 2, लेकिन दो में नहीं, जैसा कि अंजीर में है। 1, 3 और 5. लेकिन आकाश में शुक्र और सूर्य की स्थिति के सटीक मापों की मदद से, शुक्र और पृथ्वी की सटीक कक्षाओं का निर्धारण सूर्य के चारों ओर करना और गणनाओं में सुधार करना संभव है। अर्थ वही है; आकाश में शुक्र और सूर्य की स्थिति के सभी माप हमें केवल शुक्र और पृथ्वी की कक्षाओं के सापेक्ष आकार को मापने की अनुमति देते हैं। लेकिन एल _वी और एल _ई के सटीक मूल्यों को इस तरह से निर्धारित नहीं किया जा सकता है। यहां हमें एक अलग दृष्टिकोण की आवश्यकता है।

शुक्र का अंश, लंबन और सूर्य से दूरी

शुक्र के पारित होने का कारण आपको पृथ्वी की कक्षाओं के पूर्ण मूल्यों को मापने की अनुमति देता है और शुक्र है कि इस प्रक्रिया को दुनिया के विभिन्न स्थानों से उच्च सटीकता के साथ देखा जा सकता है, जिसके परिणामस्वरूप आपको सूर्य के संबंध में शुक्र के दृश्य स्थान के दो दृष्टिकोण होंगे, जो विभिन्न स्थानों से ज्ञात स्थानों से मापा जाता है। उनके बीच की दूरी। मापक लंबन आपको लंबन कोण से पृथ्वी से शुक्र की दूरी और पृथ्वी पर दो माप बिंदुओं के बीच की दूरी का सही मूल्य निर्धारित करने की अनुमति देता है - जैसे बाईं और दाईं आंखों के लिए एक अलग प्रकार की वस्तु हमारे मस्तिष्क को हमें गहराई का एहसास देने की अनुमति देती है - वस्तुओं से दूरी की भावना।


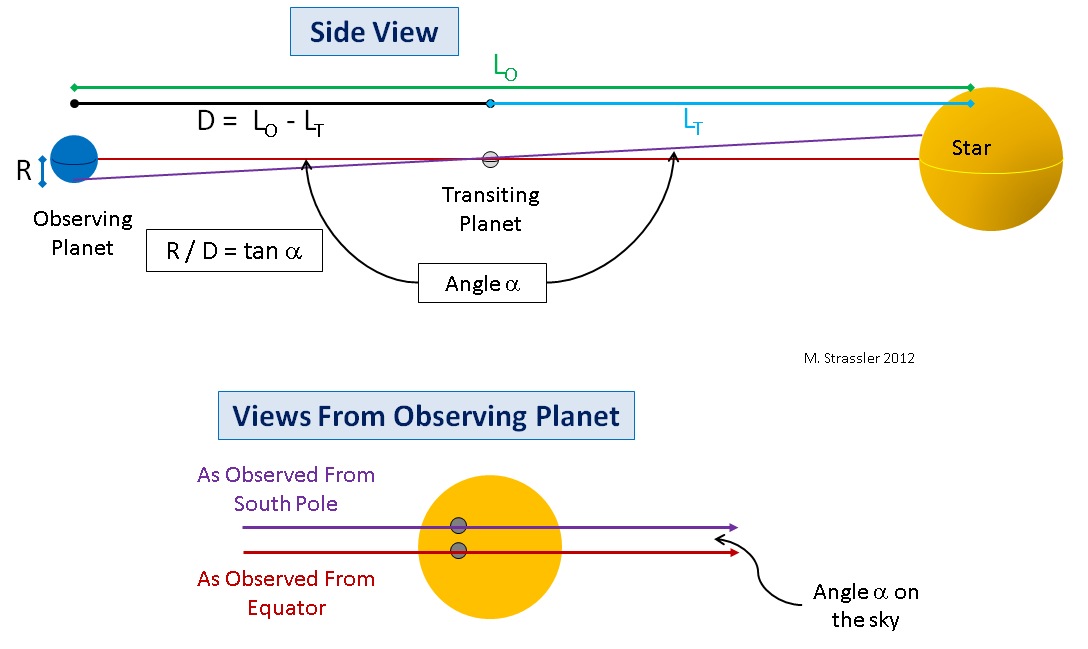
अंजीर। 6

एक प्रदर्शन के लिए, मुझे आकर्षित करना चाहिए कि यह एक बड़े ग्रह से कैसे दिखेगा। अंजीर में। चित्रा 6 उस ग्रह को दिखाता है जिसके साथ हम मार्ग का निरीक्षण करेंगे (यह पृथ्वी होगी) और ग्रह तारा के सामने से गुजर रहा है (यह शुक्र होगा)। मैं एक सरलीकृत स्थिति (सिर्फ ज्यामिति को सरल और देखने के लिए मुख्य अवधारणा को आसान बनाने के लिए) प्रस्तुत करूंगा, जिसमें ग्रह और तारा संरेखित होते हैं, इसलिए भूमध्य रेखा पर पर्यवेक्षक के दृष्टिकोण से, एक गुजरता ग्रह तारा के भूमध्य रेखा के साथ गुजर जाएगा। अंजीर में ऊपर। 6 एक पक्ष दृश्य दिखाता है; स्टार के अवलोकनशील ग्रह के भूमध्य रेखा से स्टार की डिस्क के माध्यम से गुजरने वाले ग्रह के भूमध्य रेखा से लाल रेखा पर ध्यान दें।

सही संरेखण के मामले में, बाहरी ग्रह के भूमध्य रेखा पर पर्यवेक्षक यह देखेगा कि आंतरिक ग्रह तारे के भूमध्य रेखा के साथ कैसे गुजरता है। यह अंजीर के नीचे एक लाल रेखा के रूप में दिखाया गया है। 6. लेकिन बाहरी ग्रह के दक्षिणी ध्रुव से पर्यवेक्षक यह देखेगा कि आंतरिक ग्रह तारे के भूमध्य रेखा के उत्तर में पथ (बैंगनी रेखा) के साथ कैसे गुजरता है (उत्तरी ध्रुव के मामले में, इसके विपरीत सब कुछ होगा)। यदि हम आकाश में कोण α को उन रास्तों के बीच मापते हैं जिनके साथ एक गुज़रता हुआ ग्रह चलता है और अवलोकन करने वाले ग्रह की त्रिज्या R को जानता है, तो हम एक समकोण त्रिभुज को जोड़ सकते हैं जो गुज़रते हुए ग्रह, अवलोकन करने वाले ग्रह के केंद्र और एक छोटे से कोण के साथ ग्रह के ध्रुव को जोड़ सकता है? सरल त्रिकोणमिति हमें पास के दौरान ग्रहों के बीच की दूरी डी देगी, जहां

$$

$$D = R / tan \; \ अल्फा$$

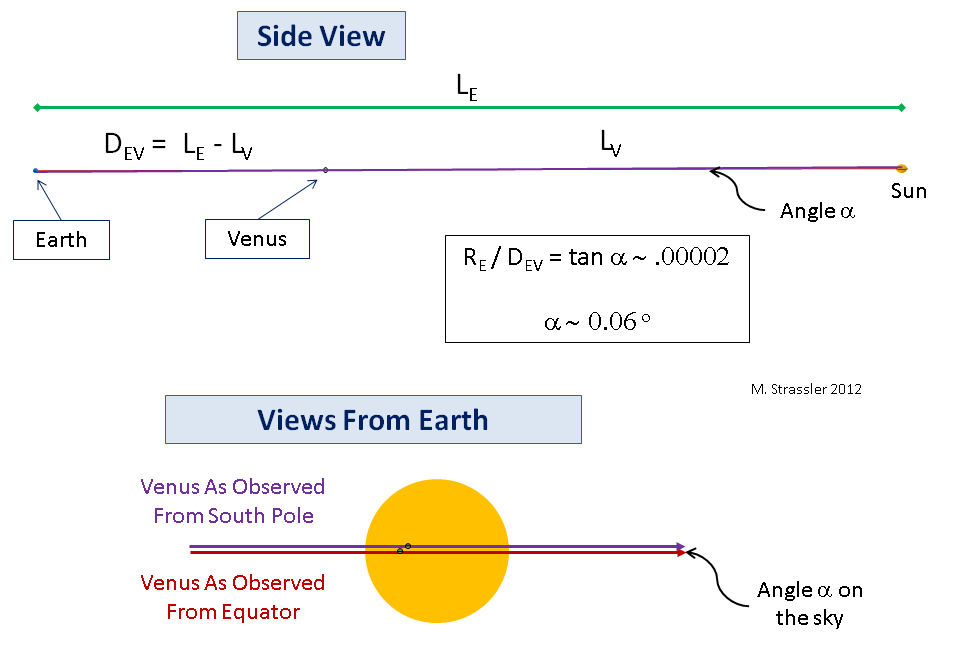
अंजीर। 7

पृथ्वी, शुक्र और सूर्य के लिए भी यही सच है, सिवाय इसके कि पृथ्वी और शुक्र उनके और सूर्य के बीच की दूरी की तुलना में इतने छोटे हैं कि कोण α लगभग 1/20 ° के बराबर होगा! (यह एक छोटी मात्रा है, लेकिन काफी औसत दर्जे का है, हालांकि सूर्य से दूरी की एक सटीक माप, जिसे 18 वीं शताब्दी के खगोलविद प्राप्त करना चाहते थे, एक छोटे कोण के परिमाण के बजाय जटिल तकनीकी रूप से सटीक माप की आवश्यकता होगी)। मैं इस तरह के एक छोटे से कोण को नहीं खींचूंगा, इसलिए आपको इसके लिए मेरा शब्द लेना होगा कि क्या हो रहा है, जो कि मैंने अंजीर में चित्रित किया है का एक संस्करण है। 6, ग्रहों और एक तारे (सूर्य) के साथ वहाँ चित्रित की तुलना में बहुत छोटा है, दूरी के संबंध में। अंजीर में भी छवि। 7 ग्रहों को अपने से बहुत बड़ा बनाता है। लेकिन यह विचार अपरिवर्तित रहता है: पारित होने के दौरान पृथ्वी और शुक्र के बीच की दूरी D _EV को लंबन कोण α (चित्र 7 के नीचे) को मापकर निर्धारित किया जा सकता है; ध्यान दें कि सूर्य का कोणीय व्यास लगभग 1/2 ° है)।

हालाँकि, अभी भी कई सवाल हैं:

• मैंने बताया कि कैसे पारित होने के दौरान पृथ्वी से शुक्र की दूरी डी _ईवी को मापना है। लेकिन क्या एल _ई और एल _वी , पृथ्वी से सूर्य और शुक्र से सूर्य की दूरी को मापने का हमारा लक्ष्य नहीं था?
• 1761 या 1769 में शुक्र के पारित होने का निरीक्षण करने के लिए कोई भी पृथ्वी के दक्षिणी ध्रुव पर नहीं गया।
• मैंने पृथ्वी, शुक्र और सूर्य की स्थिति को पूरी तरह से संरेखित किया, जैसे कि पृथ्वी के भूमध्य रेखा पर एक बिंदु से शुक्र को सूर्य के भूमध्य रेखा के साथ चलते देखा जा सकता है। लेकिन यह वास्तव में ऐसा नहीं है, और यहां तक ​​कि यह एक सामान्य वॉकथ्रू की तरह नहीं है (और 2012 में यह भी नहीं था)।
• कोण α छोटा सा सटीक रूप से मापा जा सकता है - विशेषकर फोटोग्राफी और त्वरित संदेश से पहले के दिनों में, सूर्य के उत्तरी ध्रुव के स्थान के स्पष्ट संकेत के अभाव में, जिससे पृथ्वी पर दो अलग-अलग बिंदुओं से बने शुक्र के पथ की मापों की सटीक तुलना करना मुश्किल हो जाता है। हालांकि, प्राथमिक लक्ष्य 500 (0.2%) में से 1 भाग से अधिक कोण को मापना नहीं था (हालांकि ब्लैक ड्रॉप प्रभाव के कारण, परिणाम 50 (2%) में से 1 भाग के करीब था)।

इन समस्याओं से कैसे निपटें?

सबसे पहले, आप वांछित मूल्यों, एल _ई और एल _वी को मापने के लिए डी _ईवी को मापने से कैसे जाते हैं? यह सरल है - हम पहले से ही सभी रिश्तों को जानते हैं, विशेष रूप से, हम पहले से ही एल _ई / एल _वी (लगभग, छवि 4 से, या, यदि हम समस्या को और अधिक सावधानी से जानते हैं, तो हम शुक्र के बीच अधिकतम कोण between अधिकतम से गणना कर सकते हैं और अधिक सटीक रूप से)। पृथ्वी के दृष्टिकोण से सूर्य। हम अंजीर से D _EV = L _E - L _V = L _E (1 - L _V / L _E ) भी जानते हैं। 7. इसलिए, हम एल _ई का एक अनुमानित मूल्य प्राप्त कर सकते हैं:

$$

$$L_E = D_ {EV} / (1 - L_V / L_E) = R / tan \; α / (1 - पाप \; \ गामा_ {अधिकतम})$$

जहां α पारगमन के दौरान मापा जाने वाला लंबन कोण है, और the अधिकतम शुक्र और सूर्य के बीच का अधिकतम कोण है (चित्र 5)। अधिक सटीक माप के लिए अधिक जटिल ज्यामिति की आवश्यकता होती है, लेकिन एक ही मूल विचार के साथ।

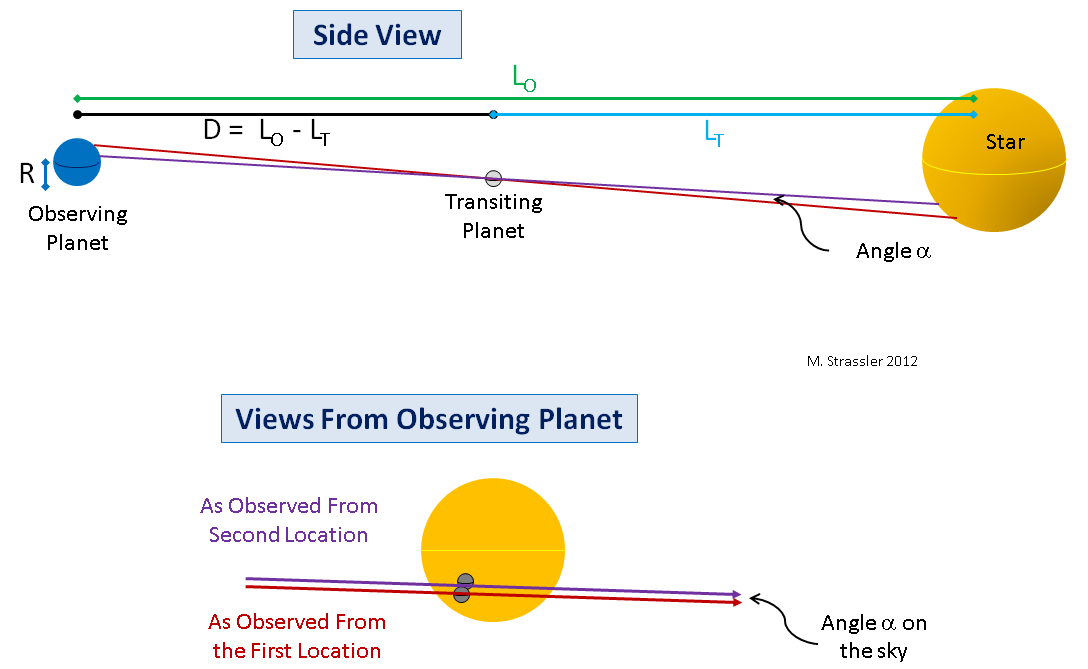
दूसरे, भले ही ग्रहों की कक्षाओं को पूरी तरह से संरेखित किया गया हो, शुक्र के पथ के दो आयामों को भूमध्य रेखा और पृथ्वी के ध्रुव से मापा नहीं जाना चाहिए। उन्हें किन्हीं दो अक्षांशों से मापा जा सकता है। ज्यामिति थोड़ी अधिक जटिल हो जाती है, लेकिन बहुत अधिक नहीं, लेकिन सिद्धांत बना रहता है (चित्र 8 देखें)।


अंजीर। 8

तीसरा, यहां तक ​​कि सही संरेखण के बिना, पृथ्वी के दो अलग-अलग बिंदुओं से मूल्यों को मापने पर एक छोटा लंबन कोण दिखाई देगा, और यदि यह कोण अच्छी तरह से मापा जाता है, तो यह माप डी में थोड़ा (अधिक जटिल समीकरणों के माध्यम से) बदल दिया जा सकता है। यह अंजीर में दिखाया गया है। 8, नीचे।

चौथा सवाल है, कोण के α से गुजरते समय शुक्र के पथ की कोणीय शिफ्ट को मापने की ऐतिहासिक रूप से जटिल समस्या हमें समय को मापने के लिए एक वैकल्पिक प्रयास की ओर ले जाती है - या तो यात्रा का समय, या बस शुरुआत और अंत की शुरुआत, और कोण नहीं। पहला विकल्प ग्रेगरी के विचारों के आधार पर हैली द्वारा प्रस्तावित किया गया था, और दूसरा, एक और सुधार के रूप में, जोसेफ निकोलस डेलिले द्वारा प्रस्तावित किया गया था। हैली विधि को पृथ्वी के विभिन्न स्थानों में घड़ी के सिंक्रनाइज़ेशन की आवश्यकता नहीं थी; इसलिए, डिल की विधि की आवश्यकता अधिक उन्नत घड़ी प्रौद्योगिकी पर आधारित थी।

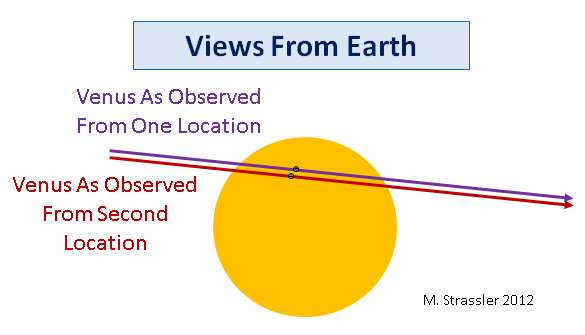
यहां तक ​​कि XVII या XVIII सदी में, एक सूर्य के डिस्क के सापेक्ष शुक्र के स्थान को मापने के लिए, विशेष रूप से एक तस्वीर की अनुपस्थिति में, सटीक रूप से अंतराल, या एक ग्रहण की शुरुआत और अंत को मापना बहुत आसान है। अंजीर में। चित्र 9 से पता चलता है कि सूर्य को पार करने वाले शुक्र के बैंगनी और लाल रास्तों की लंबाई अलग-अलग होती है क्योंकि वे इसे एक स्थान पर पार नहीं करते हैं, जिसका अर्थ है कि मार्ग की अवधि लंबन कोण से जुड़े समय से भिन्न होगी। दुर्भाग्य से, पहली नज़र में देखने पर सब कुछ अधिक जटिल हो जाता है - पृथ्वी सूर्य के चारों ओर घूमती है और घूमती है, इसलिए पर्यवेक्षक सूर्य की डिस्क के माध्यम से शुक्र के पारित होने के दौरान काफी दूरी की यात्रा करता है। इसलिए, बहुत प्रयास की आवश्यकता है (गणना काफी जटिल है, हालांकि आधुनिक कंप्यूटरों के साथ वे बहुत सरल हैं) सूर्य पर दूरी के आधार पर पृथ्वी पर दो अलग-अलग पर्यवेक्षकों द्वारा देखे गए मार्ग की शुरुआत और अंत के समय अंतराल में अंतर निर्धारित करने के लिए।

18 वीं शताब्दी की शुरुआत में हैली ने सभी आवश्यक ज्यामितीय सिद्धांतों को समझा (यदि आप उनके ग्रंथों से पुरानी अंग्रेजी वाक्यांश और शैली को घटाते हैं, तो आप आश्चर्यचकित होंगे कि उनके जटिल कथन कितने आधुनिक हैं, और आप देखेंगे कि तीन सौ साल पहले वैज्ञानिक आज के वैज्ञानिकों के समान थे। उसी बुद्धि के पास और केवल आज की वैज्ञानिक तकनीक का अभाव है)।


अंजीर। 9

यह सब बताता है कि लंबन - एक ही समय में इसे मापने वाले पर्यवेक्षकों के दृष्टिकोण से सूर्य के संबंध में शुक्र के लिए जिम्मेदार स्पष्ट स्थिति का अंतर लेकिन पृथ्वी पर विभिन्न स्थानों से - ऐतिहासिक रूप से एक बहुत ही महत्वपूर्ण तरीका है सौर प्रणाली के आकार का निर्धारण किया। आज, अधिक शक्तिशाली विधियां हमारे पास उपलब्ध हैं, लेकिन आप इस तथ्य में रुचि रख सकते हैं कि आज जो आप आकाश में देख रहे हैं, वह बहुत ऐतिहासिक महत्व का है, या आप बस हमारे सितारे के चारों ओर घूमते हुए, शुक्र के दृश्य का आनंद ले सकते हैं।