नियंत्रित करने के लिए फजी लॉजिक
पाठ वी। गोस्टेव की पुस्तक की सामग्री पर आधारित है। "स्वचालित मॉडलिंग सिस्टम में फ़ज़ी रेगुलेटर।" विषय पर सभी गंभीर प्रकाशनों की तरह, यह पुस्तक गणितीय गणनाओं से भरी हुई है और अप्रस्तुत पाठक के लिए मुश्किल है। इस बीच, अपने आप में फजी लॉजिक बनाने और उपयोग करने के सिद्धांत काफी सरल और स्पष्ट हैं। यह पाठ एक गणितीय भाषा से एक इंजीनियरिंग एक पुस्तक से एक उदाहरण का अनुवाद करने का एक प्रयास है।
फजी लॉजिक के आधार पर एक नियंत्रक को डिजाइन करने का एक संभावित अनुक्रम क्रमिक रूप से तार्किक नियमों को जटिल करने और अनुकूलन विधियों का उपयोग करके मापदंडों का चयन करके दिखाया गया है।
समस्या का बयान
हमले के कोण से एक मिसाइल नियंत्रण प्रणाली के लिए एक डिजिटल पीआईडी नियंत्रक और एक फजी नियंत्रक के संश्लेषण पर विचार करें। गणितीय मॉडलिंग का उपयोग करते हुए, हम सिस्टम में प्रक्रियाओं को निर्धारित करते हैं और संश्लेषित नियंत्रकों का उपयोग करके सिस्टम की गुणवत्ता का तुलनात्मक मूल्यांकन देते हैं।
मिसाइल के निकास समन्वय के रूप में हमले के कोण को लेना:  और इनपुट के लिए स्टीयरिंग कोण का समन्वय करें
और इनपुट के लिए स्टीयरिंग कोण का समन्वय करें  प्रपत्र में रॉकेट के हस्तांतरण समारोह को परिभाषित करें:
प्रपत्र में रॉकेट के हस्तांतरण समारोह को परिभाषित करें:
 कहां:
कहां:
 - रॉकेट रूपांतरण गुणांक,
- रॉकेट रूपांतरण गुणांक,
 - भिगोना गुणांक,
- भिगोना गुणांक,
 - समय स्थिर।
- समय स्थिर।
इसके बाद, "ट्रांसफ़र फ़ंक्शन" का उपयोग सख्त शास्त्रीय परिभाषा में नहीं किया जाता है, लाप्लास परिवर्तनों के अनुपात के रूप में।
नियंत्रण प्रणाली के अध्ययन में, मान लीजिए कि उड़ान समय पर रॉकेट के मापदंडों की निर्भरता निम्नानुसार निर्धारित की गई है:

गणनाओं को सरल बनाने के लिए, हम एकीकृत लिंक के हस्तांतरण समारोह द्वारा स्टीयरिंग तंत्र का वर्णन करते हैं  इस मामले में, सिस्टम इनपुट
इस मामले में, सिस्टम इनपुट  - हमले का कोण, सिस्टम आउटपुट
- हमले का कोण, सिस्टम आउटपुट  क्या रॉकेट द्वारा किए गए हमले के कोण, मीटर (टी) नियंत्रक के आउटपुट पर नियंत्रण संकेत है, और नियंत्रण वस्तु को सामान्य हस्तांतरण फ़ंक्शन द्वारा वर्णित किया गया है:
क्या रॉकेट द्वारा किए गए हमले के कोण, मीटर (टी) नियंत्रक के आउटपुट पर नियंत्रण संकेत है, और नियंत्रण वस्तु को सामान्य हस्तांतरण फ़ंक्शन द्वारा वर्णित किया गया है:

(एनालॉग स्टीयरिंग गियर और रॉकेट को कंट्रोल ऑब्जेक्ट में शामिल किया गया है)।
बहुपद द्वारा इनपुट कार्रवाई की भिन्नता का नियम दिया गया है:

एक नियंत्रक विकसित करना आवश्यक है जो पीआईडी नियंत्रक और फजी लॉजिक के आधार पर एक नियंत्रक का उपयोग करके इनपुट प्रभाव के विकास को सुनिश्चित करता है।
नियामकों के गुणांक का चयन करने के लिए।
पीआईडी नियंत्रक और फजी लॉजिक के आधार पर नियंत्रक के साथ क्षणिक की तुलना करें।
गतिशील वस्तु मॉडल
एक संरचनात्मक मॉडलिंग वातावरण में एक गतिशील मॉडल बनाएं।
मॉडल सर्किट स्वयं चित्र 1 में दिखाया गया है।
निर्दिष्ट कार्रवाई एक स्थिर ब्लॉक के रूप में सेट की जाती है, स्क्रिप्ट से एक चर को पैरामीटर के रूप में सेट किया जाता है। संक्रमण फ़ंक्शन के पैरामीटर चर के रूप में सेट किए गए हैं।
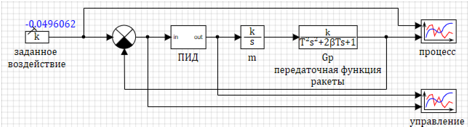 चित्रा 1. एक रॉकेट के एक गतिशील मॉडल का आरेख।
चित्रा 1. एक रॉकेट के एक गतिशील मॉडल का आरेख।नियामक सेटिंग
पीआईडी ब्लॉक एक सबमॉडल (छवि 2) है, जो मानक ब्लॉक "असतत पीआईडी नियंत्रक" का उपयोग करता है। नमूने की दर 0.001 सेकंड के बराबर चुनी गई है।
 चित्रा 2. ट्यूनिंग सर्किट के साथ पीआईडी नियंत्रक।
चित्रा 2. ट्यूनिंग सर्किट के साथ पीआईडी नियंत्रक।नियंत्रक मापदंडों को प्रोजेक्ट
Kp, Ki, Kd के वैश्विक सिग्नल नामों के रूप में सेट किया जाता है
। यह आपको सिमुलेशन के दौरान मापदंडों को बदलने, और नियामक को समायोजित करने की अनुमति देता है।
"ऑप्टिमाइज़ेशन" ब्लॉक का उपयोग नियामक को समायोजित करने के लिए किया गया था; अनुकूलन मानदंड न्यूनतम मानक विचलन है।
अनुकूलन इकाई संक्रमण प्रक्रिया के दौरान अनुकूलन करती है। अनुकूलन परिणाम तीन गुणांक का एक वेक्टर है, जो "संकेतों की सूची में लिखें" ब्लॉक को भेजा जाता है, जहां गणना किए गए मान संकेतों में स्थानांतरित किए जाते हैं और तदनुसार, पीआईडी गुणांक के मान बदल जाते हैं। नियंत्रक को कॉन्फ़िगर करने के लिए, हम निम्नलिखित अनुकूलन पैरामीटर निर्धारित करते हैं:
सभी गुणांक के प्रारंभिक मूल्य
1।चयन के लिए सीमा
-50 से
+50 निर्धारित की गई है
चयन सटीकता
0.001अनुकूलन
0.01 के बाद अधिकतम मानक विचलन
इस मामले में, अनुकूलन इकाई ने गुणांक के निम्नलिखित इष्टतम मूल्यों की गणना की:
केपी = -1.7498597; की = 17.891995; केडी = 11.606602 ।
इन गुणांक के साथ, दिए गए क्षणिक में मानक विचलन
0.008738090 था

चित्रा 3. क्षणिक।
| 
चित्रा 4. प्रबंधन। |
फजी लॉजिक कंट्रोलर
फजी लॉजिक पर आधारित नियंत्रक के मुख्य लाभ वस्तु को नियंत्रित करने के लिए नियमों के गठन की सादगी और स्पष्टता है।
उदाहरण के लिए, "ऑटोमैटिक मॉडलिंग सिस्टम में फजी रेगुलेटर" पुस्तक में, हमले के कोण द्वारा रॉकेट को नियंत्रित करने के लिए फजी विनियमन नियम गणितीय अभिव्यक्ति के रूप में वर्णित हैं:

जहां,

- सिस्टम त्रुटि, गति परिवर्तन (पहली व्युत्पन्न) त्रुटियां, त्वरण (दूसरी व्युत्पन्न) त्रुटियां;
एम - ऑब्जेक्ट पर नियंत्रण कार्रवाई;

- त्रुटि का भाषाई अनुमान, त्रुटि के परिवर्तन की दर (त्रुटि का पहला व्युत्पन्न) और त्रुटि का दूसरा व्युत्पन्न, एक सार्वभौमिक सेट पर परिभाषित फ़ज़ी सेट के रूप में माना जाता है।

;

- ऑब्जेक्ट पर नियंत्रण कार्रवाई का भाषाई अनुमान, चर
एम के टर्म-सेट से चुना गया है
पाठक पूछ सकता है: यह कैसे है, तुम्हारी माँ, मुझे खेद है, समझे?
कभी-कभी मुझमें संदेह पैदा हो जाता है कि गणितज्ञ स्वयं समझते हैं कि उन्होंने क्या लिखा है। अचानक गणितीय मोड़ के पीछे, फजी विनियमन के नियमों का महान रहस्य छिपा हुआ है। यहाँ यह है:
बहुत कम करें
मानदंड - स्पर्श न करें
छोटा - वृद्धियदि आप पक्षी की भाषा से रूसी भाषा में अनुवाद करते हैं, तो अभिव्यक्ति

शाब्दिक अर्थ है निम्नलिखित:
यदि यह
सामान्य से अधिक है और
विचलन बढ़ता है और
विकास दर बढ़ती है , तो हम
घट जाते हैं ।
यदि
मानदंड नहीं बदलता है और
गति स्थिर है , तो हम
नहीं बदलते हैं ।
यदि यह
सामान्य से कम है और
गिरता है और
गिरने की दर बढ़ जाती है , तो
बढ़ें ।
यदि आप समझते हैं कि गणितीय धूमिल के पीछे वास्तव में क्या छिपा है, तो आप नियामकों के निर्माण को अधिक सचेत रूप से संपर्क कर सकते हैं और अधिक दिलचस्प परिणाम प्राप्त कर सकते हैं।
सिद्धांत की बिट
हमले के कोण को समायोजित करने की समस्या को हल करने के लिए, हमें निरंतर विचलन मूल्य से तीन शर्तें प्राप्त करनी चाहिए - कम, आदर्श, अधिक। वही विचलन के पहले व्युत्पन्न और विचलन के दूसरे व्युत्पन्न के लिए किया जाना चाहिए। यह फजी इनविज़न का पहला चरण है - चरणबद्ध।
शर्तें प्राप्त करने के लिए, हमें प्रत्येक शब्द के लिए पैरामीटर का संख्यात्मक मान सेट करना होगा। उदाहरण के लिए: "लिटिल" = -1; "सामान्य" = 0; "कई" = 1. चरणबद्ध करने के लिए हम त्रिकोणीय कार्यों का उपयोग करेंगे। जैसे-जैसे आप सेट मूल्य के करीब आते जाते हैं, वैसे-वैसे कार्य बढ़ते जाते हैं और जैसे-जैसे आप दूर जाते जाते हैं, घटते जाते हैं। त्रिकोणीय कार्यों के दो विकल्प चित्र 5 में दिखाए गए हैं:

 चित्रा 5. त्रिकोणीय सदस्यता कार्य।
चित्रा 5. त्रिकोणीय सदस्यता कार्य।विचलन (एक्स 1) को जानते हुए, हम सदस्यता फ़ंक्शन के मूल्यों को अधिक (लाल रेखा), मानदंड (ग्रीन लाइन), कम (नीली रेखा) के लिए पा सकते हैं। मान 0 से 1 तक होंगे।
कृपया ध्यान दें कि बाएं चार्ट पर चरम फ़ंक्शन काफी "त्रिकोणीय" नहीं हैं। अगर हम इसे अमूर्त गणित के दृष्टिकोण से मानते हैं, तो सही ग्राफ पर कार्य अधिक "सुंदर" हैं। लेकिन, यदि आप "फजी निष्कासन के नियमों का मुख्य रहस्य" याद करते हैं, तो बाएं चार्ट अधिक सही है। वास्तव में:
नियम
"Add - small" पर विचार करें, यदि हमारे पास -1 का मान है, तो
"थोड़ा" = 1 (लाल रेखा) अन्य ग्राफ़ के लिए सही है। और अगर हमारे पास -2 का मूल्य है? तार्किक रूप से, हमें भी
जोड़ना चाहिए। बाएं ग्राफ पर -2 यह है:
"थोड़ा = 1" , लेकिन सही ग्राफ पर हमारे पास
"थोड़ा" = 0 है, जो स्पष्ट रूप से सच है। नियम के लिए भी यही सच है
"बहुत कम करें ।
""ईमानदार" त्रिकोणीय कार्यों द्वारा चरणबद्धता इस तथ्य को जन्म दे सकती है कि जब मूल्य कार्यों की परिभाषा की सीमा से परे होता है, तो हमें सभी शर्तों के लिए 0 मिलता है, जो बदले में, वस्तु पर प्रभाव की अनुपस्थिति का कारण बन सकता है।
उलटा समस्या का निराकरण है। प्रभाव की गणना करने के लिए, आपको व्युत्क्रम परिवर्तन करने की आवश्यकता है - हमारे पास सदस्यता कार्यों के मूल्य कम करने के लिए हैं, परिवर्तन नहीं, सीमा में वृद्धि (
0 ... 1 ) (त्रिकोणीय फ़ंक्शन) और उन प्रभावों की श्रेणी जो हमारे पास हो सकती है, और हमें तीन शब्दों में से एक होना चाहिए संख्या एक विशिष्ट प्रभाव है।
आप विभिन्न तरीकों से प्रभाव प्राप्त कर सकते हैं, उदाहरण के लिए, आंकड़े के द्रव्यमान के केंद्र में। चित्रा 6 नियंत्रक की स्थिति को दर्शाता है, जहां शर्तों में कमी आती है
0.3 के मान
0.6 में बदलाव नहीं करते हैं और
0.8 को नियामक प्रभाव
-30..30 के परिणामस्वरूप
बढ़ाते हैं जिसके परिणामस्वरूप प्रभाव
4.1 होता है।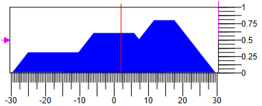 चित्रा 6. नियंत्रण कार्रवाई की अवहेलना
चित्रा 6. नियंत्रण कार्रवाई की अवहेलनाडिफैसिफिकेशन का एक अन्य विकल्प बिंदुओं के द्रव्यमान के केंद्र में है। चित्र 7 में एक विकल्प दिखाया गया है, जहां समान मानों और नियंत्रण सीमा के लिए, हमें एक और उत्तर
8.82 मिलता है:
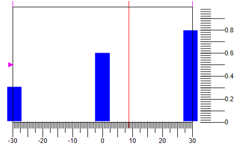 चित्र 7. बिंदुओं के द्रव्यमान के केंद्र द्वारा अवक्षेपण।
चित्र 7. बिंदुओं के द्रव्यमान के केंद्र द्वारा अवक्षेपण।यह समझा जाना चाहिए कि निष्कर्ष की विधि के अलावा, सदस्यता फ़ंक्शन का आकार भी परिणाम को प्रभावित करता है। उदाहरण के लिए, आप ऐसे त्रिभुजाकार कार्य चुन सकते हैं, जिसके लिए त्रिभुज का आधार समान हो, केवल कोने भिन्न हों। (अंजीर देखें। 8)।
 चित्रा 8. एक आधार के साथ त्रिकोणीय सदस्यता कार्य।
चित्रा 8. एक आधार के साथ त्रिकोणीय सदस्यता कार्य।इस स्थिति में, चरण 0.3 के समान मानों के साथ चरणीकरण के परिणाम को कम करने के लिए, 0.6 को न बदलें और नियामक प्रभाव -30 की सीमा के साथ -0.8 को बढ़ाएं, 30 परिणामी प्रभाव =
5.27 ।
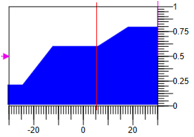 चित्रा 9. क्षेत्र की गणना के द्वारा डिफैजीफिकेशन।
चित्रा 9. क्षेत्र की गणना के द्वारा डिफैजीफिकेशन।फ़ज़ी लॉजिक के गुप्त ज्ञान से लैस, हम एक नियंत्रक मॉडल बनाएंगे। हम रॉकेट मॉडल को पीआईडी नियंत्रक (छवि 1 देखें) के लिए छोड़ देते हैं, लेकिन नियंत्रक के सबमॉडल में हम चित्र 10 में दिखाए गए सर्किट को इकट्ठा करते हैं।
 चित्र 10. फजी लॉजिक पर आधारित कंट्रोलर सर्किट।
चित्र 10. फजी लॉजिक पर आधारित कंट्रोलर सर्किट।नियामक के प्रवेश द्वार पर, दिए गए कोण पर हमले और वास्तविक (मापा) के बीच एक बेमेल लागू होता है। इनपुट के बाद एक "एक्सट्रापोलेटर" ब्लॉक होता है, जो एक दिए गए नमूने की अवधि के साथ एक असतत में निरंतर संकेत के रूपांतरण को प्रदान करता है (0.001 s एक असतत पीआईडी नियंत्रक के समान है)।
इसके बाद, पहले और दूसरे व्युत्पन्न विचलन की गणना की जाती है। ऐसा करने के लिए, हम वर्तमान मूल्य और मान के बीच के अंतर की गणना करते हैं, जो कि परिमाणीकरण अवधि के लिए देरी के साथ है, इसे विलंब समय (तुलना ब्लॉक में गुणांक) से विभाजित करें। इस प्रकार, हमें तीन इनपुट मिलते हैं: सिस्टम त्रुटि, त्रुटि की दर (पहली व्युत्पन्न), त्रुटि का त्वरण (दूसरा व्युत्पन्न)।
इनपुट वैरिएबल का मान चरणकरण ब्लॉकों द्वारा त्रिकोणीय कार्यों में परिवर्तित किया जाता है। प्रत्येक चर के लिए, हमें तीन भाषाई चर (कुल नौ) मिलते हैं।
Demultiplexer नियम बनाने के लिए भाषाई चर में वैक्टरों को प्रजनन करता है। आरेख में, वैक्टर में उनके क्रम के क्रम में चर के नाम पर हस्ताक्षर किए जाते हैं।
हमारे मामले में विचलन सेट और मापा के बीच का अंतर है, अगर एक नकारात्मक मूल्य का मतलब है कि हमले का कोण सेट से अधिक है, तो हमें इसे कम करना होगा। और तदनुसार, इसके विपरीत, यदि विचलन सकारात्मक है, तो मापा कोण निर्दिष्ट एक से कम है, हमें इसे बढ़ाना होगा।
(अधिक - कम, कम - वृद्धि, आदर्श - स्पर्श न करें) ।
आउटपुट में तीन भाषाई चर "कम", "परिवर्तन नहीं", "वृद्धि" भी हैं। मल्टीप्लेक्स एक वेक्टर में मूल्यों को एकत्र करता है और इसे फजी आउटपुट ब्लॉक में भेजता है। अब जब हमारे पास सभी चर हैं, तो हम आरेख नियमों को एक आरेख के रूप में लिख सकते हैं।
- यदि सामान्य से अधिक और विचलन बढ़ता है और विकास दर बढ़ती है => कमी होती है।
- यदि मान नहीं बदलता है और स्थिर है => हम नहीं बदलते हैं।
- यदि यह सामान्य से कम है और गिरता है और गिरने की दर => बढ़ जाती है।
नियमों में सभी भाषाई चर तार्किक ब्लॉक "और" के माध्यम से जुड़े होते हैं और आउटपुट से जुड़े होते हैं। जैसा कि चित्र 10 से देखा जा सकता है, तार्किक फजी इनवेंशन सर्किट व्यावहारिक रूप से सामान्य लॉजिकल सर्किट से अलग नहीं है, केवल फजी लॉजिक ब्लॉक का उपयोग किया जाता है।
पीआईडी नियंत्रक को ट्यूनिंग करने के समान, हम अनुकूलन ब्लॉक का उपयोग करते हैं।
सवाल ब्लॉकों के मापदंडों के साथ रहता है।
फजी लॉजिक के आधार पर एक नियंत्रक का संश्लेषण
कुछ भी नहीं के लिए जीवन में कुछ भी नहीं दिया जाता है, और इसलिए, विनियमन नियमों की सादगी की भरपाई सदस्यता कार्यों का वर्णन करने वाले मापदंडों की संख्या से की जाती है। वास्तव में, यदि आपको पीआईडी नियंत्रक के लिए तीन गुणांक का चयन करने की आवश्यकता है, तो फ़ज़ी लॉजिक के मामले में, केवल एक त्रिकोणीय फ़ंक्शन को कोने के लिए 3 नंबर की आवश्यकता होती है। यदि प्रत्येक इनपुट चर के लिए हमें आउटपुट के लिए 3 सदस्यता कार्यों + 3 की आवश्यकता होती है, तो यह पता चलता है कि हमें 3 x 3 x 3 + 3 x 3 = 36 पैरामीटर सेट करने की आवश्यकता है!
लेकिन सब कुछ इतना दुखद नहीं है। पहले सन्निकटन और प्रारंभिक सेटअप के लिए, सब कुछ सरल किया जा सकता है।
नियंत्रक के प्रारंभिक समायोजन के लिए कुछ धारणाएँ बनाना:
- हम शून्य के संबंध में फ़ंक्शन की समरूपता निर्धारित करते हैं, फिर अधिकतम और न्यूनतम दो संख्याओं के बजाय, आप एक - अधिकतम निर्दिष्ट कर सकते हैं और, तदनुसार, एक सीमा के रूप में परिभाषित किया जाएगा [ -मैक्स ... मैक्स ]।
- हम फ़ंक्शन का एक समान वितरण सेट करते हैं, फिर हम दिए गए रेंज के आधार पर त्रिकोण के सभी कोने की स्थिति की गणना कर सकते हैं।
- तीन कार्यों के लिए, कोने के निर्देशांक को परिभाषित किया जाता है -मैक्स, 0, मैक्स।
- हम निर्धारित करते हैं कि सभी सदस्यता कार्यों के त्रिकोण का आधार समान है।
इस प्रकार, 36 स्वतंत्र मापदंडों के बजाय, हमें केवल 4 निर्दिष्ट करना चाहिए, तीन इनपुट चर और एक आउटपुट के लिए 0 से अधिकतम विचलन, अर्थात्:
uMax - नियंत्रण क्रिया का आयाम
(-uMax ... uMax) ;
deltaMax - अधिकतम विचलन
(-deltaMax ... deltaMax) ;
divMax - विचलन का अधिकतम व्युत्पन्न
(-DivMax ... divMax) ;
Div2Max - विचलन का अधिकतम दूसरा व्युत्पन्न
(-Div2Max ... div2Max)चरणबद्धता और फजी निष्कर्ष के कार्यों में, हम स्वीकार किए गए मान्यताओं को ध्यान में रखते हुए मापदंडों की गणना करने के लिए इन संकेतों का उपयोग करते हैं।
वी.वी. गोस्टेव द्वारा पुस्तक में प्रस्तावित नियंत्रक सेटिंग "स्वचालित मॉडलिंग सिस्टम में फ़ज़ी रेगुलेटर", तीन सदस्यता कार्यों द्वारा चरणबद्धता के मामले के लिए, निम्नलिखित पैरामीटर प्रस्तावित हैं:
uMax = 30 - नियंत्रण क्रिया का आयाम;
डेल्टमैक्स = 0.01 - अधिकतम विचलन;
divMax = 0.07 - विचलन का अधिकतम व्युत्पन्न;
div2Max = 1 विचलन का अधिकतम दूसरा व्युत्पन्न है।
क्षणिक तुलना
ग्राहकों के ग्राफ पर, किसी दिए गए प्रभाव का संयोग और प्राप्त परिणाम लगभग पूरा हो गया है:

चित्रा 11. ए क्षणिक। पीआईडी नियंत्रक
| 
चित्रा 11. बी क्षणिक। फजी लॉजिक
|
स्पष्ट अंतर को प्राप्त विचलन और नियंत्रण कार्रवाई के ग्राफ पर देखा जा सकता है:

चित्रा 12. ए। प्रबंधन। पीआईडी नियंत्रक
| 
चित्र 12. ब। प्रबंधन। फजी लॉजिक |
आंकड़ों की तुलना से, यह देखा जाता है कि फजी नियंत्रक कम त्रुटि, और बेहतर क्षणिक प्रदान करता है।
यदि हम एक स्टेपवाइज कंट्रोल एक्शन सेट करते हैं तो सिस्टम में ट्रांज़ेक्टर्स की तुलना करते हैं। चित्र 13 में परिणाम:

चित्रा 13. ए। चरण प्रभाव। पीआईडी नियंत्रक।
| 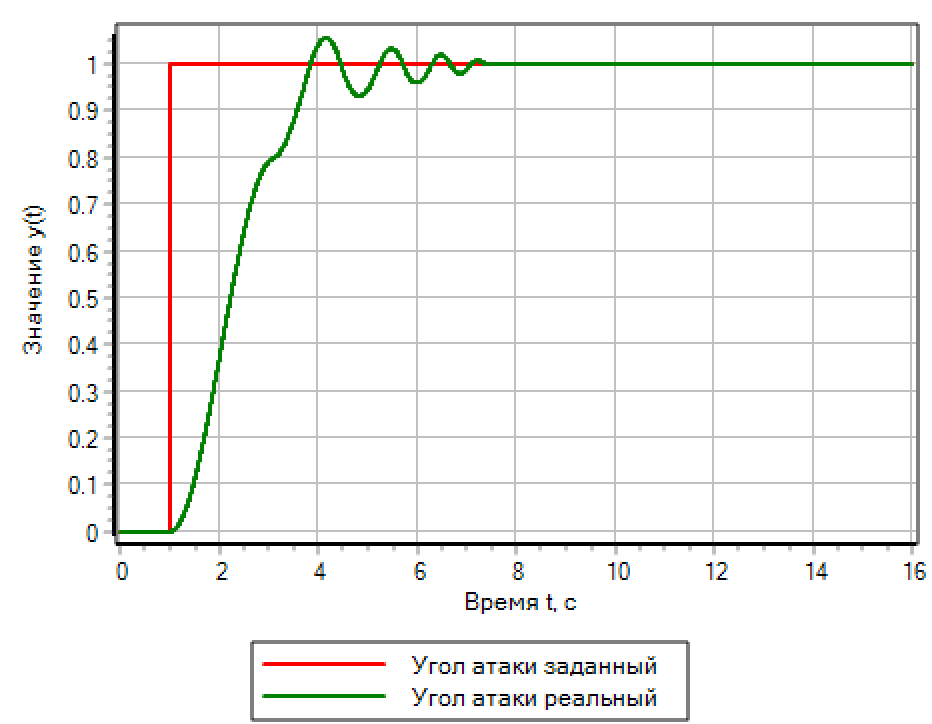
चित्र 13. ब। चरण प्रभाव। फजी लॉजिक। |
स्टेप वाइज एक्शन के लिए, एक फजी लॉजिक आधारित कंट्रोलर सबसे अच्छा क्षणिक गुण प्रदान करता है। पीआईडी नियंत्रक, जो स्वचालित रूप से एक चिकनी प्रक्रिया पर सेट होता है, ओवरशूट के साथ दोलनों का कारण बनता है जो दो बार निर्धारित चरण होते हैं।
अनुकूलन विधि द्वारा फ़ज़ी लॉजिक के आधार पर नियंत्रक का समायोजन
चलो अनुकूलन विधि द्वारा फ़ज़ी कंट्रोलर के मापदंडों को चुनने की कोशिश करते हैं, जैसे हमने उन्हें पीआईडी नियंत्रक के लिए चुना था। एक मानदंड के रूप में, हम मानक विचलन को 0.001 से कम निर्धारित करते हैं।
यह ध्यान दिया जाना चाहिए कि यह विधि पूरी तरह से सही नहीं है, क्योंकि पेशेवरों के लिए यह स्पष्ट है कि कौन सा कोण और कौन सी गति प्रत्येक संगीत कार्यक्रम के टुकड़े के लिए अधिकतम और न्यूनतम है, जो आपको अनुकूलित मापदंडों पर प्रतिबंधों को और अधिक सचेत रूप से सेट करने की अनुमति देता है, हम डिफ़ॉल्ट पैरामीटर सेट करते हैं और ऐसा होता है।
डिफ़ॉल्ट सेटिंग्स के साथ अनुकूलन विधि ने अनुकूलन मापदंडों की सीमाओं के निम्नलिखित मूल्यों की गणना की:
uMax = 19.377 - नियंत्रण क्रिया का आयाम;
डेल्टमैक्स = 1.095 - अधिकतम विचलन;
divMax = 0.01 - विचलन का अधिकतम व्युत्पन्न;
div2Max = 2.497 विचलन का अधिकतम दूसरा व्युत्पन्न है।
विचलन के एक सरल अनुकूलन के मामले में, प्राप्त पैरामीटर निर्दिष्ट सटीकता प्रदान करते हैं, हालांकि, यह नियंत्रण कार्रवाई के उच्च आवृत्ति दोलनों का कारण बनता है।
संक्रमण फ़ंक्शन और नियंत्रण क्रियाएं चित्र 14.a में प्रस्तुत की गई हैं
 चित्रा 14. ए। फजी लॉजिक। विचलन सेटिंग। चित्रा 14. ए। फजी लॉजिक। विचलन सेटिंग।
| 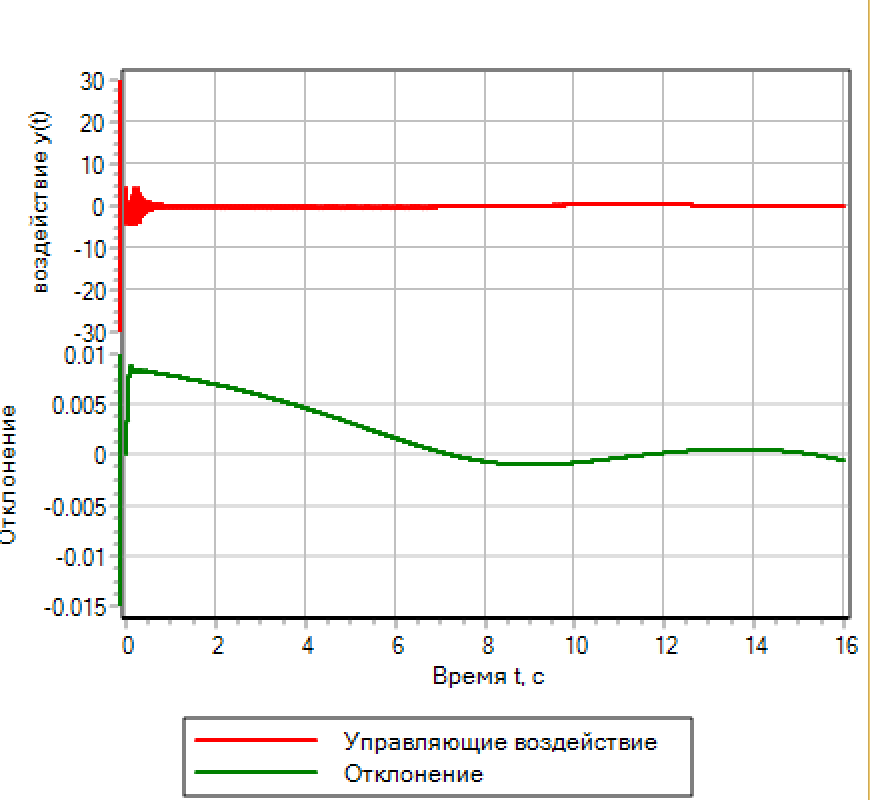 चित्र 14. बी। फजी लॉजिक। विचलन और प्रतिक्रियाओं की संख्या द्वारा सेटिंग। चित्र 14. बी। फजी लॉजिक। विचलन और प्रतिक्रियाओं की संख्या द्वारा सेटिंग। |
क्षणिक प्रक्रिया को बेहतर बनाने के लिए, एक अनुकूलन मानदंड को विनियमित कर सकते हैं नियामक विनियमन की संख्या नकारात्मक से सकारात्मक मूल्य के प्रभाव (छवि 15 में योजना)।
 चित्रा 15. 2 मानदंडों द्वारा अनुकूलन के लिए योजना।
चित्रा 15. 2 मानदंडों द्वारा अनुकूलन के लिए योजना।दो मापदंड के अनुसार अनुकूलन विधि द्वारा गणना निम्नलिखित पैरामीटर मान देती है:
uMax = 19.714 - नियंत्रण क्रिया का आयाम;
डेल्टमैक्स = 1.0496 - अधिकतम विचलन;
divMax = 0.01 - विचलन का अधिकतम व्युत्पन्न;
div2Max = 1.7931 विचलन का अधिकतम दूसरा व्युत्पन्न है।
यह देखा जा सकता है कि जब अनुकूलन मानदंड में यात्राओं की संख्या जोड़ी गई थी, तो नियंत्रक की स्विचिंग आवृत्ति को कम करना संभव था (देखें अंजीर। इस प्रकार, हम कह सकते हैं कि ऑप्टिमाइज़ेशन विधि तब भी काम करती है जब हम ऑब्जेक्ट की भौतिकी के बारे में कुछ नहीं जानते हैं और केवल उनके भौतिक अर्थ के बारे में सोचे बिना संख्यात्मक मापदंडों का चयन करते हैं।
फजी लॉजिक के आधार पर अपना कंट्रोलर बनाना
ऊपर, हमने पहले से ही तैयार और काफी सरल योजना के अनुसार नियंत्रक बनाया, भाषाई चर के सभी शब्द तार्किक ऑपरेटर I से जुड़े थे। चूंकि हमारे पास इनपुट और आउटपुट पर समान शब्द हैं, इसलिए यह सबसे सरल और सबसे स्पष्ट समाधान है।
आइए एक नियंत्रक बनाने की कोशिश करें जिसके आउटपुट में 3 शब्द नहीं हैं, लेकिन, उदाहरण के लिए, 5:
जल्दी से कम करें, कम करें, बदलें नहीं, बढ़ें, जल्दी बढ़ें । और प्रवेश द्वार पर ही।
, .
:
1)
=> .2)
=> .3)
=> .4)
=> .5)
=> .5 (5 ). ,
-uMax +uMax., , , (. . 5).
.
(.. 7).
15.
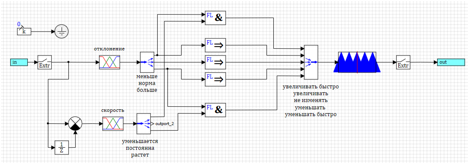 15. .
15. .«». , , .
16.
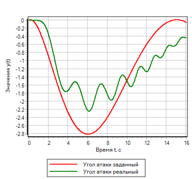 16. .
16. ., , . , , . , , , .
1)
=> .2)
=> .3)
=> .4)
=> .5)
=> .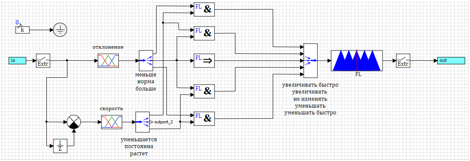 17. .
17. ., 18 18.

18.. .
| 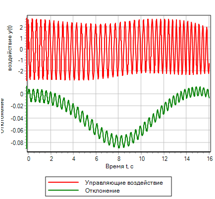
18.. |
. , , . , . 19 , , , 1.
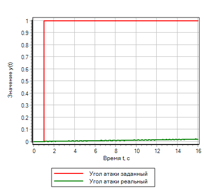
19.. .
| 
19.. . |
, , . , , . , , :
1)
=> .2) (
)
=> .3)
=> .4) (
)
=> .5)
=> .20.
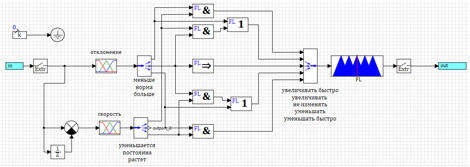 20. .
20. ., , (. . 21).
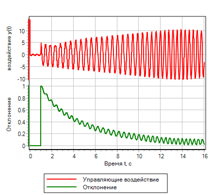
21.. .
| 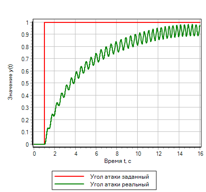
21.. . |
, «» .
, , . , , , .
, . , , . , , , :
1)
=> .2) (
)
=> .
3)
=> .4) (
)
=> .5)
=> .
22. «», , , «
& ».
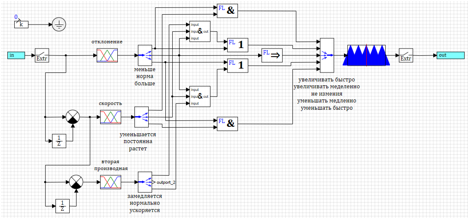 22. .
22. ., :
uMax = 27.4983 – ;
deltaMax = 0.0433 – ;
divMax = 0.0966 – ;
div2Max = 1.0828 – .
23. , , . – .
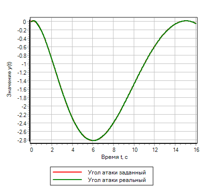
23.. .
| 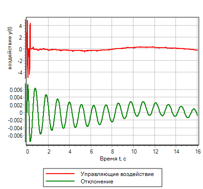
23.. . |
निष्कर्ष
, -.
.
. .
, ,
...