🕒 😖 🦇 एक हवाई जहाज से उतरने वाले पैराट्रूपर के द्रव्यमान के केंद्र की गति के बैलिस्टिक-टेम्पोरल विशेषताओं का निर्धारण 🏂🏽 🏜️ ✌️

परिचय

पैराट्रूपर के द्रव्यमान के केंद्र की गति की बैलिस्टिक-टेम्पोरल विशेषताओं को निर्धारित करने के लिए, एक को एक सरलीकृत गणितीय मॉडल चुनना होगा जो विश्लेषणात्मक अनुसंधान के लिए काफी सुलभ है और साथ ही मूल वस्तु की सबसे विशिष्ट विशेषताओं को संरक्षित करता है।

पैराट्रूपर के आंदोलन के सरलीकृत गणितीय मॉडल बनाने के लिए, निरंतर और समय मापदंडों का विश्लेषण, निर्धारण, व्यवस्थितकरण किया जाता है।

Nonlinear गणितीय मॉडल के निर्माण के लिए नियमित और पर्याप्त रूप से उचित तरीके वर्तमान में मौजूद नहीं हैं, हालांकि, विशेष समस्याओं को हल करने के लिए, nonlinear अंतर समीकरणों की प्रारंभिक प्रणालियों की सही तैयारी के साथ, उन्हें हल करने के लिए संख्यात्मक तरीके काफी पर्याप्त परिणाम दे सकते हैं।

इस प्रकाशन का उद्देश्य विभेदक समीकरणों की प्रणाली को संकलित और संख्यात्मक रूप से हल करना है जो एक हवाई जहाज से एक पैराट्रूपर के आंदोलन के सभी चरणों का वर्णन करता है, जो वायु के घनत्व घनत्व की ऊंचाई और तापमान में परिवर्तन के प्रभाव को ध्यान में रखता है।

एक पैराट्रूपर की गति की बैलिस्टिक-टेम्पोरल विशेषताएं

लगातार और सीमित चर मापदंडों में शामिल हैं:

एन पैराशूटिस्ट की ऊंचाई है;
वि ० - विमान की गति;
के - वजन, पैराट्रूपर की ऊंचाई;
g गुरुत्वाकर्षण का त्वरण है;
ρ वायु घनत्व है;
T हवा का तापमान है।

अस्थायी (परिवर्तनशील) मापदंडों में शामिल हैं:

tn - लैंडिंग समय,
w हवा की गति है;
वी पैराट्रूपर की गति है;
यू आरोही (अवरोही) प्रवाह की गति है;
डी - बहाव (प्रोजेक्शन बिंदु की जमीन पर प्रक्षेपण से टचडाउन बिंदु तक दूरी);
सी लैंडिंग ऑब्जेक्ट का ड्रैग गुणांक है;
F - लैंडिंग ऑब्जेक्ट का midsection।

कूदने की अवस्था

पहला चरण विमान से अलग होने के बाद एक नि: शुल्क गिरावट है:

दूसरा चरण एक स्थिर पैराशूट में कमी है:

स्थिर पैराशूट की मुख्य संपत्ति मुख्य पैराशूट के लिए सबसे सुविधाजनक स्थिति में पैराशूटिस्ट का स्थिरीकरण है।

तीसरा चरण - मुख्य पैराशूट के गुंबद को भरना:

चौथा चरण खुले पैराशूट में कमी है:

पैराशूट जंप के सभी चरणों के लिए विभेदक समीकरणों की एक प्रणाली का संकलन

हम इजेक्शन पॉइंट O पर केंद्रित एक निश्चित समन्वय प्रणाली OXY चुनते हैं। धुरी OX विमान की गति के क्षैतिज घटक की दिशा के साथ मेल खाता है। ओई अक्ष को पैराशूटिस्ट के ऊर्ध्वाधर वेग के विपरीत दिशा में लंबवत निर्देशित किया जाता है।

हम मान लेंगे कि पैराट्रूपर की गति सपाट है, और ओएक्सवाई विमान में होती है। कूद के इस मॉडल को हवा के प्रभाव को ध्यान में रखे बिना शांत मौसम में एक कूद का मॉडल माना जा सकता है।

हम मानते हैं कि, वजन के अलावा, पैराट्रूपर पैराट्रूपर की गति के वर्ग के आनुपातिक वायु प्रतिरोध के बल से प्रभावित होता है:

।
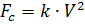
जहां:

।

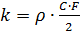
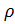
- वायु घनत्व, सी - गुणांक खींचें, एफ - शरीर के midsection।

बढ़ती ऊंचाई के साथ, हवा का तापमान बदल जाता है:

न्यूनतम तापमान पहले से ही 10 किमी की ऊंचाई पर पहुंच गया है। और -55 ° C है। वायु घनत्व भी दबाव पर निर्भर करता है। इसलिए, पैराशूट जंप के बैलिस्टिकों की गणना करते समय, वायु घनत्व निर्धारित करने के लिए निम्न सूत्र का उपयोग करना सुविधाजनक होता है: 1:

।
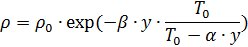
जहाँ

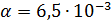
के / एम;

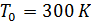
- समुद्र तल पर तापमान; y, m में ऊँचाई है;

- y = 0 पर वायु घनत्व;

।

लिस्टिंग

# -*- coding: utf8 -*- from numpy import* import matplotlib.pyplot as plt beta=1.25*10**-4 alfa=6.5*10**-3 T0=300 y=arange(0,10000,1) x=[exp(-beta*w*T0/(T0-alfa*w)) for w in y] plt.title("  \n    ") plt.plot(x,y) plt.ylabel('  .') plt.xlabel(' ') plt.grid(True) plt.show()

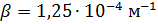
गणना के अभ्यास में, विकास का वर्ग midsection के रूप में लिया जाता है; C का मान तालिका [2] से पाया जाता है:

Θ मार्ग के झुकाव के कोण को दर्शाता है। घटकों के लिए बनाई गई मान्यताओं के तहत

।

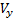
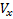
वेग वैक्टर वी हमारे पास है:

परिणामी प्रणाली और denoting के समीकरणों के बाएँ और दाएँ पक्ष को m द्वारा विभाजित करना

आर के माध्यम से, हम प्राप्त करते हैं:

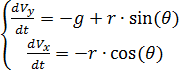
(1)

हम फ़ंक्शन V, t, y (t), x (t) के लिए अंतर समीकरणों की एक प्रणाली के रूप में एक स्काइडाइवर की गति के समीकरणों को लिखते हैं।

यह देखते हुए कि:

।

।
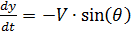
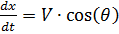
और विभेदित समय अनुपात:

, समीकरणों की प्रणाली को ध्यान में रखते हुए (1) हमें मिलता है:

।

।

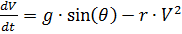
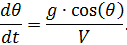
इस प्रकार, प्रारंभिक शर्तों के तहत:

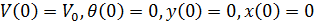
हमारे पास अंतर समीकरणों की निम्नलिखित प्रणाली है:

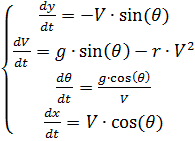
पायथन का उपयोग करके अंतर समीकरणों (2) की एक प्रणाली का संख्यात्मक समाधान

हल करने के लिए (2), हम इसे निम्नलिखित रूप में लिखते हैं, समय और वायु घनत्व द्वारा नियंत्रित ड्रैग बलों को स्थिर करते हुए

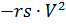
और मुख्य

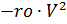
पैराशूट, क्रमशः, टाइम कंट्रोल फ़ंक्शंस ks (t) और ko (t) द्वारा गुणा किया जाता है:

।

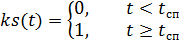
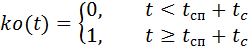
जहां:

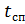
—प्रातुरूप से मुक्त होने का समय;

- मुख्य एक के उद्घाटन तक स्थिरीकरण पैराशूट का परिचालन समय।

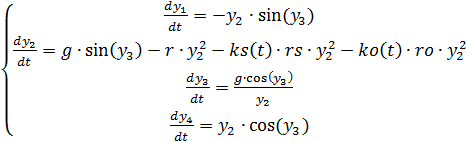
(3)

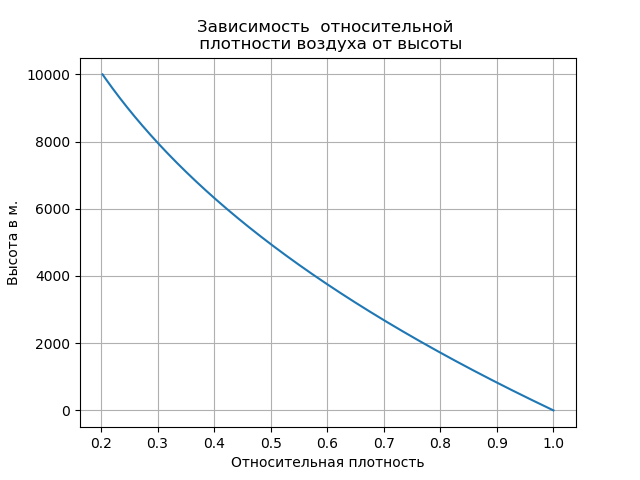
वायु घनत्व में परिवर्तन के लिए समायोजित कार्यक्रम की पूरी सूची

 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#   /2 rou0=1.29#  /3 Cp=0.3#    Cpar=0.75#     mp=120#    100+20=120 . s=0.8#   2 ss=1.5#   2 Cpars=0.35#     S=70#   2 tsp=40#    c. tssp=3 #      c. tpr=210#     . h=4000.0#    . V0=100.0#    / beta=1.25*10**-4 alfa=6.5*10**-3 T0=300 def ks(t): if t<= tsp: z=0 else: z=1 return z def ko(t): if t<= tsp+tssp: z=0 else: z=1 return z def f(y,t): y1,y2,y3,y4=y rou=rou0*exp(-beta*y1*T0/(T0-alfa*y1)) rp=0.5*Cp*rou*s/mp rpars=0.5*Cpars*rou*ss/mp rpar=0.5*Cpar*rou*S/mp return [-y2*sin(y3),g*sin(y3)-rp*(y2**2)-ko(t)*rpar*(y2**2)-ks(t)*rpars*(y2**2),g*cos(y3)/y2,y2*cos(y3)] t=arange(0,tpr,1) y0=[h,100,0,0] [y1,y2,y3,y4]=odeint(f, y0,t, full_output=False).T plt.figure() plt.title('     : %s .. \n   : %s /. \n   : %s /'%(h,V0,round(y2[tpr-tsp-tssp],0))) plt.plot(y1,y2*sin(y3),label='  .: %s c. \n     : %s . \n     : %s . '%(tsp,tssp,tpr-tsp-tssp)) plt.xlabel('  .') plt.ylabel('   /') plt.legend(loc='best') plt.grid(True) plt.figure() plt.title("-         \n   ") plt.plot(y1,y4) plt.xlabel('  .') plt.ylabel('     .') plt.grid(True) plt.figure() plt.title("     ") plt.plot(t,y2*sin(y3)) plt.xlabel('  .') plt.ylabel('   /.') plt.grid(True) plt.show()

हमें मिलता है:

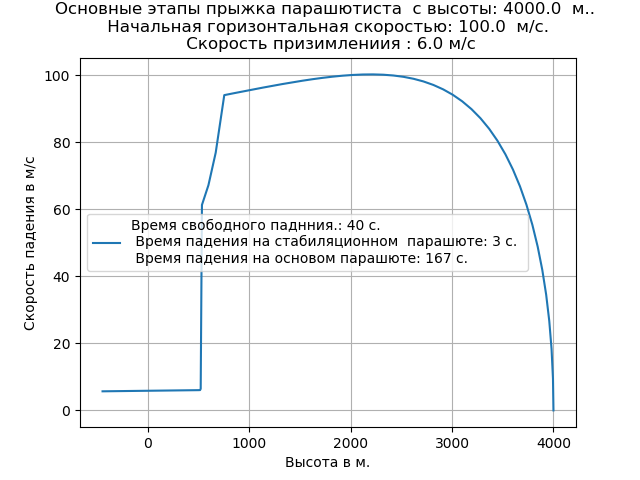
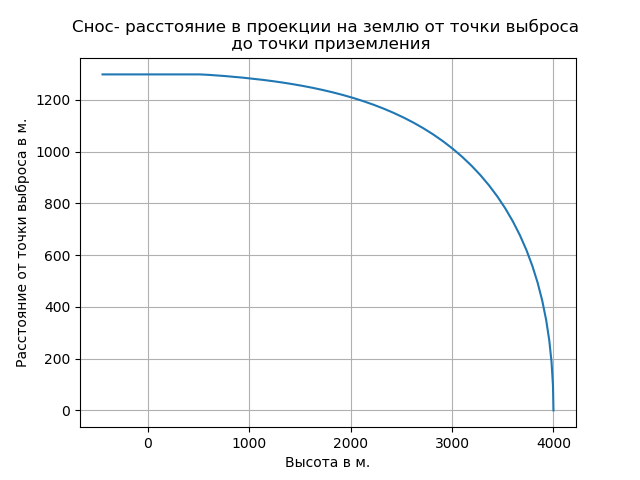
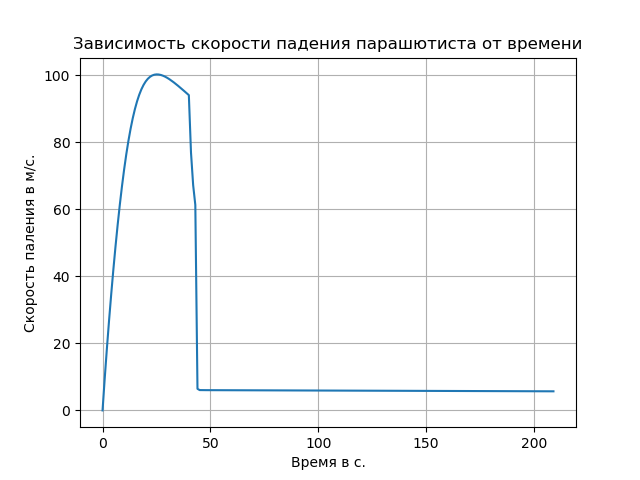
दुर्लभ हवा को ध्यान में रखते हुए मुक्त गिरावट की दर में वृद्धि हुई और इस खंड में प्रक्षेपवक्र की प्रकृति को बदल दिया।

इस समस्या को दो अंतर समीकरणों की एक प्रणाली की मदद से हल किया जा सकता है, जो नीचे दिए गए हैं (पैराशूट को छोड़कर और वायु घनत्व में परिवर्तन):

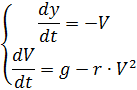
प्रतिरोध बलों और वायु घनत्व में परिवर्तन को स्पॉइलर के नीचे लिस्टिंग में दिखाया गया है, ऊपर और स्पष्टीकरण के बिना ध्यान में रखते हुए

# - * - कोडिंग: utf8 - * -
खस्ता आयात से *
scipy.integrate आयात odeint से
प्लेट के रूप में आयात matplotlib.pyplot
एम = 100
r0 = 1.3
सी 1 = 0.3
c2 = 0.6
c3 = 0.5
c4 = 0.75
एस = 70
s = 0.8
ss = १.५
जी = 9.8
tsp = 6
tsbp = 10
tp = 90.0
एच = 1000.0
बीटा = 1.25 * 10 ** - 4
अल्फा = 6.5 * 10 ** - 3
T0 = 300
डीईएस केएस (टी):
अगर t <tsp:
z = 0
बाकी:
z = 1
वापसी Z
डीओ को (टी):
यदि t <tsp + tsbp:
z = 0
बाकी:
z = 1
वापसी Z
# dy1 / dt = y2
# dy2 / dt = g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * 4 * y2 ** 2) / मी
डी एफ (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0.5 * r * c1 * s
k2 = 0.5 * r * c2 * s
k3 = 0.5 * r * c3 * ss
k4 = 0.5 * r * c4 * S
वापसी [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / एम]
t = arange (0.0, tp)
y0 = [h, 0.0]
[y1, y2] = odeint (f, y0, t, full_output = False .TT
plt.title ("1000 और 800 मीटर से स्काइडाइविंग")
plt.plot (y1, y2, लेबल = 'ऊँचाई 1000 मीटर')
एच = 800.0
tsp = 6
tsbp = 2
tp = 80.0
डीईएस केएस (टी):
अगर t <tsp:
z = 0
बाकी:
z = 1
वापसी Z
डीओ को (टी):
यदि t <tsp + tsbp:
z = 0
बाकी:
z = 1
वापसी Z
डी एफ (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0.5 * r * c1 * s
k2 = 0.5 * r * c2 * s
k3 = 0.5 * r * c3 * ss
k4 = 0.5 * r * c4 * S
वापसी [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / एम]
t = arange (0.0, tp)
y0 = [h, 0.0]
[y1, y2] = odeint (f, y0, t, full_output = False .TT
plt.plot (y1, y2, लेबल = 'ऊँचाई 800 मीटर')
plt.xlabel ('मीटर में ऊँचाई।')
plt.ylabel ('m / s में बर्निंग स्पीड')
plt.legend (loc = 'best')
plt.grid (सच)
plt.show ()

हमें मिलता है:

निष्कर्ष

एक हवाई जहाज से उतरने वाले पैराट्रूपर के द्रव्यमान के केंद्र की गति की बैलिस्टिक-टेम्पोरल विशेषताएं निर्धारित की जाती हैं।

संदर्भ

वायुमंडलीय दबाव।
गेरासिमेंको आई। ए। एयरबोर्न प्रशिक्षण: पाठ्यपुस्तक। एम .: सैन्य प्रकाशन, 1986. भाग 1, पी। 32।

एक हवाई जहाज से उतरने वाले पैराट्रूपर के द्रव्यमान के केंद्र की गति के बैलिस्टिक-टेम्पोरल विशेषताओं का निर्धारण