परिचय

यह संक्षिप्त नोट इस बारे में बात करेगा कि वायुमंडलीय प्रकाश के प्रकीर्णन के मॉडल को जेटलैग द्वारा हमारे अंतिम 4k int Appear में कैसे संरचित किया गया है , का पार्टी संस्करण, जिसमें इस वर्ष के अप्रैल में संशोधन 2018 की पार्टी में 4k इंट्रो कम्पो में एक सम्मानजनक 12 वां स्थान जीता है।

आप यहां बिना एसएमएस के बाइनरी को मुफ्त में डाउनलोड कर सकते हैं ।

यदि, हालांकि, आपके पास विंडोज नहीं है, या यदि आपके पास एक शक्तिशाली आधुनिक वीडियो कार्ड नहीं है, तो एक आराम से मूर्ख है:

इस काम के लिए संगीत 4klang का उपयोग करके उत्सुक द्वारा लिखा गया था। सभी कोड और विजुअल मेरे पीछे रहे।

यहां हम केवल प्रकाश के बिखरने के मॉडल के बारे में बात करेंगे। अन्य चीजें, जैसे उपकरण, एक शहर का एक मॉडल, प्रकाश व्यवस्था और सामग्री का मॉडल, प्रभावित नहीं होते हैं। मैं बहादुर लोगों को स्रोत पढ़ने के लिए भेज सकता हूं, या रिकॉर्डिंग देख सकता हूं कि मैं घंटों तक कैसे डूब रहा हूं - अधिकांश विकास वीडियो पर किया गया है।

याद करने के लिए एक उबाऊ कहानी

इस काम पर काम इस बोध के साथ शुरू हुआ कि मुख्य पूर्णकालिक नौकरी के लिए एक पूर्ण 4k नौकरी पर काम करने के लिए समय नहीं बचता है - यह आंगन में पहले से ही लगभग मार्च के मध्य में है, कुछ हफ़्ते तक Revizen तक छोड़ दिया जाता है।
यह केवल कुछ के लिए एक सरल कुछ के साथ आने के लिए बनी हुई है, शाम की एक जोड़ी के लिए, कम्पो फिलर। एक और बेवकूफ री-मार्च करने के लिए दर्शक का सम्मान नहीं करना है, इसलिए मुझे याद आया कि कुछ साल पहले मुझे बिखरने के साथ एक शेडर करना था, और यह काफी सरल, कॉम्पैक्ट और एक ही समय में पारगम्य सुंदर था, यद्यपि यह धीरे-धीरे धीमा था।

एक छोटी चर्चा के दौरान, मैंने अपने दम पर जोर दिया, और हमने निम्नलिखित पर ध्यान केंद्रित करने का फैसला किया: विसरित प्रकाश से भरे परिदृश्य को बनाने के लिए, सूर्यास्त, बादलों और गोधूलि किरणों के साथ (टीआईएल के रूप में अभिव्यक्ति "भगवान की किरणों का अनुवाद किया गया")। वातावरण में चरणों की संख्या को पूरी तरह से गैर-संवादात्मक मूल्यों को नहीं उठाने के लिए, आपको दृढ़ता से (जैसे मोंटे कार्लो आंगन विधि) खड़खड़ाना होगा, जो दृश्य शोर उत्पन्न करेगा। लेकिन इससे कोई फर्क नहीं पड़ता कि आप कैमरा को स्थानांतरित करते हैं और धीरे-धीरे दृश्य बदलते हैं और परिवेश ट्रैक शुरू करते हैं, आप दर्द को आसन्न फ्रेम को मिला सकते हैं और इस शोर को अस्थायी रूप से समाप्त कर सकते हैं।

कीन ने संगीत को बहुत जल्दी लिखा - यह संशोधन से दो सप्ताह पहले लगभग तैयार था। हालांकि, मैं फ्लू से गंभीर रूप से अपंग था - एक एम्बुलेंस और एक संक्रामक बीमारी के साथ - इसलिए मैंने व्यावहारिक रूप से उस समय तक शेडर पर काम करना शुरू नहीं किया जब तक कि कम या ज्यादा किसी भी तरह से जीवित स्थिति में मैं फ्रैंकफर्ट के लिए एक विमान पर चढ़ गया। इस बिखरने वाले मॉडल का प्रोटोटाइप हवा में पहले से ही लिखा गया था।

हमने समय सीमा से पहले और शेष कुछ घंटों के लिए पार्टी में रेत और लार से इंट्रा के पार्टी संस्करण को पहले ही व्हॉट्स अप कर लिया था (और, शायद, एक के बाद; डी), जबकि मैं एक साथ फ्लू से दूर जा रहा था, नींद की कमी, घंटों लंबी उड़ानें, और शेडर शोडाउन लाइवकोडिंग कम्पो में भाग लेने से वह लगातार विचलित था।

बड़े स्क्रीन पर दिखाए गए संस्करण में बहुत सारी कलाकृतियाँ थीं और शहर की केवल अल्पविकसित ज्यामिति थी जो वोरोनोई आरेख पर यादृच्छिक ऊँचाइयों पर आधारित थी।

सामान्य तौर पर, 12 वां स्थान काफी उदार है।

ऊपर दिखाया गया अंतिम संस्करण, बाद में और अधिक आराम से बनाया गया था, एक महीने के लिए सप्ताह में 1-2 बजे। कुल मिलाकर, इसे काम करने में लगभग 40-50 घंटे लगे।

तितर बितर मॉडल

(नोट: मैं पेशेवर रूप से ग्राफिक्स प्रोग्रामिंग नहीं करता हूं। अच्छे के लिए यह मेरा छोटा सा शौक है, अगर सौ या दो के तहत बहुत डीफोकस किया जाता है बियर प्रति वर्ष शराब के घंटे। इसलिए, कोई शून्य संभावना नहीं है कि कुछ चीजें नीचे वर्णित हैं और / या गलत तरीके से नाम दिया गया है। चाचा, मारो!)

बिखरने वाले मॉडल को पूरी तरह से बेदखल किए गए एपिपोलर नमूने के साथ, पुस्तक जीपीयू प्रो 5 में प्रकाशित ईगोर युसोव द्वारा "हाई परफॉर्मेंस आउटडोर लाइट स्कैटरिंग यूज एपिलेटर सैम्पलिंग" लेख से उधार लिया गया है।

भौतिक मॉडल

सूर्य के फोटोन पृथ्वी के वायुमंडल पर बमबारी करते हैं और वायु कणों के साथ संपर्क करते हैं। एक फोटॉन को एक कण द्वारा बिखेरा जा सकता है, जो फोटॉन की दिशा में बदलाव को रोकता है, या इसे अवशोषित किया जा सकता है, जिसका अर्थ है कि फोटॉन खो गया है, और इसकी ऊर्जा को किसी अन्य रूप में परिवर्तित कर दिया गया है।
दोनों प्रक्रियाएं संभाव्य हैं और विशेष रूप से कण घनत्व और फोटॉन ऊर्जा (जो इसके रंग से मेल खाती है) पर निर्भर करती हैं।

उंगलियों पर, "लाल" फोटॉनों में हवा के साथ बातचीत करने की कम संभावना होती है, इसलिए वे वायुमंडल की मोटाई को अपेक्षाकृत बरकरार रखते हैं।
नीले रंग के लोगों में, हालांकि, बिखरने की अधिक संभावना होती है, यही वजह है कि वे पर्यवेक्षक के बार-बार दिशा बदलने और वातावरण में काफी दूरी तय करने से पहले (या नहीं) पर्यवेक्षक तक पहुंच सकते हैं।

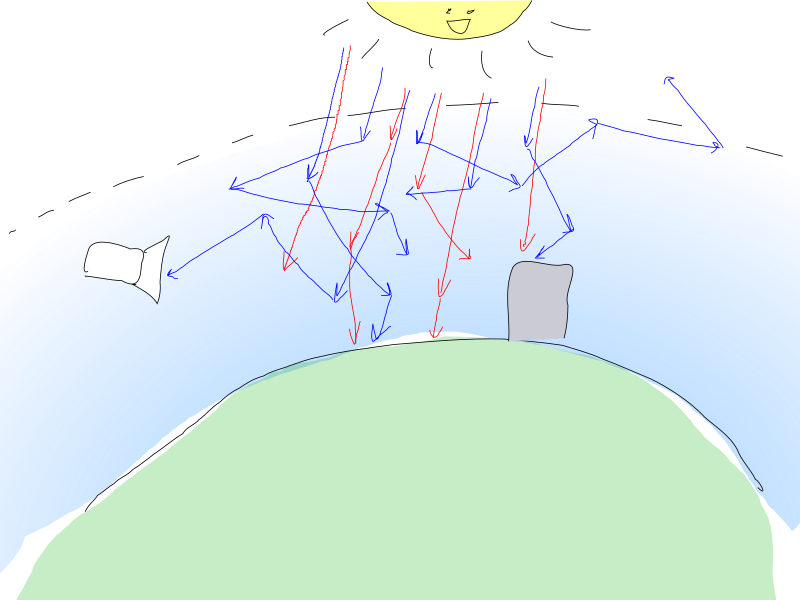
हवा के साथ प्रकाश की बातचीत के पैरामीटर जो हमें रुचि रखते हैं, इस प्रकार हैं:

• $$$\ beta ^ s (x)$ - एक बिंदु पर प्रति इकाई लंबाई में बिखरे हुए प्रकाश का अंश $$$x$
• $$$\ बीटा ^ (x)$ - एक बिंदु पर अवशोषित प्रकाश प्रति इकाई लंबाई का अंश $$$x$
• $$$\ बीटा ^ ई (एक्स) = \ बीटा ^ एस (एक्स) + \ बीटा ^ ए (एक्स)$ - एक बिंदु पर प्रति यूनिट लंबाई में खोई हुई रोशनी का कुल अंश $$$x$
• $$$p (\ Alpha)$ बिखरे हुए प्रकाश का कोणीय वितरण है, जहां $$$\ अल्फा$ यह घटना और बिखरे बीम के बीच का कोण है

यह माना जाता है कि हवा में दो प्रकार के कण होते हैं, जिनमें से बिखरना स्वतंत्र रूप से होता है: अणु (रेले मॉडल) और एरोसोल (अपेक्षाकृत बड़े गोलाकार कण, अंग्रेजी भाषा के साहित्य में माई बिखरने )। उपरोक्त मापदंडों के लिए मॉडल केवल भिन्न मूल्यों में भिन्न होते हैं।

दोनों मॉडल के लिए, यह माना जाता है कि संबंधित कणों का घनत्व ऊंचाई के साथ तेजी से घटता है: $$$\ rho = \ rho_0e ^ {- \ frac {h} {H}}$ जहाँ $$$\ rho_0$ - समुद्र तल पर घनत्व। गुणांक $$$\ बीटा$ आनुपातिक $$$\ rho$ , और उनके अर्थ नीचे समुद्र स्तर के लिए दिए गए हैं।

रेले मॉडल

• $$$p_R (\ अल्फा) = \ frac {3} {16 \ pi} (1+ \ cos ^ 2 (\ अल्फा))$ [निशिता एट अल। 93, प्रीथम एट अल। 99]
• $$$\ Beta_R ^ a = 0$
• $$$\ mathbf {\ beta_R ^ e} = \ mathbf {\ beta_R ^ s} = = (5.8, 13.5, 33.1) _ {rgb} 10 ^ {- 6} m ^ {- 1}$ [रिले एट अल। 04, ब्रुनेटन और नेरेट 08]
• $$$H_R = 7994m$ [निशिता एट अल। 93]

एरोसोल

• $$$p_M (\ अल्फा) = \ frac {1} {4 \ pi} \ frac {3 (1-g ^ 2)} {2 (2 + g ^ 2)} \ frac {1+ \ cos ^ 2 (\ _) अल्फा)} {(1 + g ^ 2 - 2g \ cos (\ अल्फा)) ^ \ frac {3} {2}}$ [निशिता एट अल। 93, रिले एट अल। 04] कहां $$$g = 0.76$ [ब्रूनटन और नेरेट 08]
• $$$\ Beta_M ^ s = 2 \ cdot10 ^ {- 5} m ^ {- 1}$ [ब्रूनटन और नेरेट 08]
• $$$\ Beta_M ^ e = 1.1 \ beta_M ^$
• $$$H_M = 1200m$ [निशिता एट अल। 93]

एकल प्रकीर्णन सन्निकटन

प्रकीर्णन सन्निकटन कैमरे के प्रत्येक पिक्सेल से एक बीम के उत्सर्जन पर आधारित है और इस दिशा से वातावरण को कितना प्रकाश मिलना चाहिए, इसकी गणना की गई है। प्रत्येक किरण सभी तीन आरजीबी प्रकाश घटकों से मेल खाती है, जैसे कि संबंधित किरणों वाले तीन फोटॉन इस किरण के साथ उड़ते हैं।

कक्ष में पहुंचने वाली रोशनी हवा में निम्नलिखित प्रक्रियाओं द्वारा निर्मित होती है:

• छितराया हुआ (टीआईएल जो अंजीर को बिखेरना सीखता है) सीखता है। सूर्य द्वारा उत्सर्जित प्रकाश को जोड़ा जाता है, जो संभवतया कैमरे की दिशा के अनुरूप कोण द्वारा बिखरा हुआ है।
• अवशोषण । बीम के साथ पहले से उड़ने वाला प्रकाश हवा द्वारा अवशोषित होता है।
• तितर बितर करना । बीम के साथ पहले से ही उड़ने वाला प्रकाश अन्य दिशाओं में बिखरने के लिए खो जाता है।

प्रदर्शन कारणों से, हमारा मानना ​​है कि प्रकाश केवल एक बार बिखरने से कैमरे की दिशा में आ सकता है, और अन्य सभी प्रकाश (जो एक से अधिक बार बिखरे हुए थे) को उपेक्षित किया जा सकता है। यह गोधूलि के लिए अनुशंसित नहीं है, लेकिन क्या करना है।

यह दृष्टिकोण निम्नलिखित सुंदर छवि में दिखाया गया है (मैंने कोशिश की!):

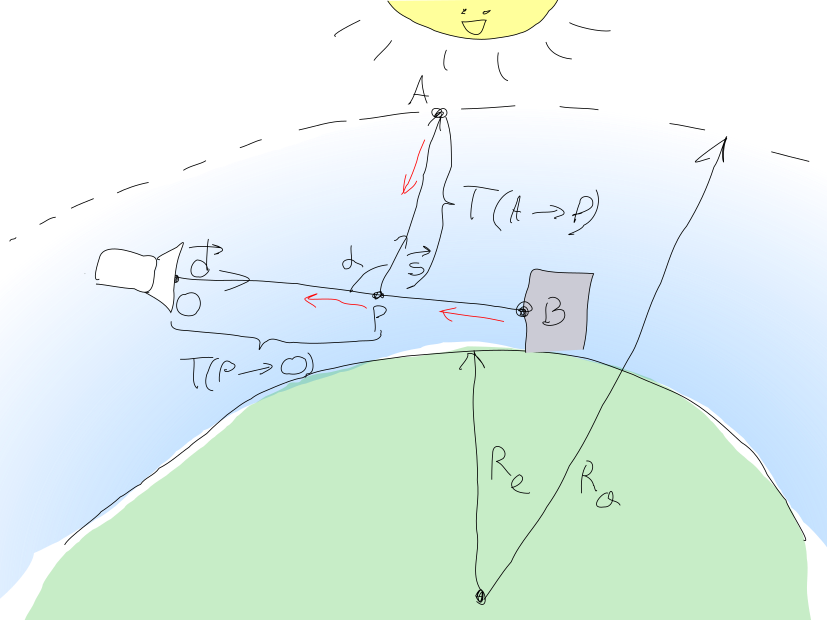
इस प्रकार, कैमरा पिक्सेल द्वारा प्रकाश की मात्रा का पता लगाया जाना चाहिए $$$O$ की राशि के रूप में गणना की जा सकती है $$$\ mathbf {L} = \ mathbf {L_ {in}} + \ mathbf {L_ {{}}$ जहाँ $$$\ mathbf {L_ {in}}$ - सूरज से विसरित प्रकाश, और $$$\ mathbf {L_ {BO}}$ - बिंदु से प्रकाश की मात्रा $$$ब$ वस्तु ज्यामिति दृश्य तक पहुँचना $$$O$ ।

प्रकाश ज्यामिति

$$$\ mathbf {L_ {BO}} = \ mathbf {L_O} e ^ {- \ mathbf {T} (B \ rightarrow O)}$ जहाँ $$$\ mathbf {L_O}$ क्या प्रकाश एक बिंदु से उत्सर्जित होता है $$$ब$ कैमरे की ओर।

$$$\ mathbf {T} (B \ rightarrow O)$ बिंदुओं के बीच के माध्यम की ऑप्टिकल मोटाई कहलाती है $$$ब$ और $$$O$ , और गणना इस प्रकार है:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ int_B ^ O (\ beta_M ^ e) (s) + \ mathbf {\ beta_R ^ e} (s) ds$$

जबकि सदस्य $$$\ बीटा$ समुद्र स्तर के स्थिर और परिवर्तनशील घनत्व से मिलकर, इस अभिव्यक्ति को निम्न में बदला जा सकता है:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ beta_M ^ e \ cdot \ int_B ^ O \ rho_M (s) ds + \ mathbf {\ beta_R ^ e} \ _ intho ^ O \ rho_R (s) ds = \ _ बार {\ mathbf {\ beta}} \ cdot \ bar {T_ \ rho} (B \ rightarrow O)$$

कृपया ध्यान दें कि मैं विशेष रूप से खुलासा नहीं करता हूं $$$\ rho$ , क्योंकि बादलों को जोड़ने पर हम उन्हें बाद में बदल देंगे। मैं इस तथ्य की ओर भी ध्यान आकर्षित करता हूं कि $$$\ बीटा$ - आरजीबी वैक्टर (कम से कम) $$$\ mathbf {\ beta_R}$ आरजीबी घटकों के लिए अलग-अलग अर्थ हैं, और $$$\ beta_M$ - सदिश सिर्फ स्थिरता के लिए)। सदस्यों के साथ $$$\ rho$ अभिन्न के तहत स्केलर हैं।

सूरज की रोशनी

सूरज की रोशनी $$$\ mathbf {L_ {in}}$ सभी बिंदुओं पर एकीकरण द्वारा गणना की गई $$$पी$ खंड के साथ $$$ओब$ और कैमरे की ओर आने वाली सभी धूप का संचय और मोटाई में मर रहा है $$$\ mathbf {T} (P \ rightarrow O)$ ।

सूर्य के प्रकाश की मात्रा एक बिंदु तक पहुँचती है $$$पी$ एक समान सूत्र द्वारा गणना की जाती है $$$\ mathbf {L_P} = \ mathbf {L_ {sun}} e ^ {- T (A \ rightarrow P)}$ जहाँ $$$\ mathbf {L_ {sun}}$ - सूरज की चमक, और $$$ए$ वह बिंदु है जिस बिंदु से किरण $$$पी$ सूरज की ओर $$$\ vec {s}$ वातावरण छोड़ देता है। इस प्रकाश का अंश जो कैमरे की ओर बिखरा होगा, वह है $$$\ mathbf {L_P} \ cdot (\ mathbf {\ beta_R ^ s} (s) p_R (\ अल्फा) + \ beta_M ^ s (s) p_M (\ अल्फा))$ ।

कुल हमें मिलता है:

$$

$$\ mathbf {L_ {in}} = \ int_B ^ O \ mathbf {L_P} (s) \ cdot (\ beta_M ^ s (s) p_M (\ अल्फा) + \ mathbf {beta_R ^ s} (s) p_R ((अल्फा)) \ cdot e ^ {- \ mathbf {T} (P (s) \ rightarrow O)} ss$$

आप देख सकते हैं कि:

• $$$\ अल्फा$ कैमरे के प्रत्येक पिक्सेल-रे के लिए एक स्थिर है (हम मानते हैं कि सूरज असीम रूप से दूर है और इससे निकलने वाली किरणें समानांतर हैं)
• गुणांक $$$\ बीटा$ समुद्र तल के स्थिरांक और घनत्व कार्यों दोनों से मिलकर $$$\ rho (s)$
• कार्यों $$$p (\ Alpha)$ दोनों बिखरने की प्रक्रियाओं के लिए सामान्य कारक हैं

यह आपको अभिव्यक्ति को निम्न में बदलने की अनुमति देता है:

$$

$$\ mathbf {L_ {in}} = \ mathbf {L_ {sun}} (1+ \ cos ^ 2 (\ Alpha)) (\ frac {\ frac {1} {4 \ pi} \ frac / 3 (1) -g ^ 2)} {2 (2 + g ^ 2)}} {(1 + g ^ 2 - 2g \ cos (\ अल्फा)) ^ \ frac {3} {2}} \ Beta_M ^ s \ cdot \ mathbf {I_M} + \ frac {3} {16 \ pi} \ mathbf {\ beta_R ^ s} \ cdot \ mathbf {I_R})$$

जहाँ

$$

$$\ mathbf {I_M} = \ int_B ^ O \ rho_M (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} ds$$

$$

$$\ mathbf {I_R} = \ int_B ^ O \ rho_R (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} ds$$

$$$I_m$ और $$$I_R$ केवल घनत्व कार्यों में भिन्नता होती है, उनके घातांक समान होते हैं।

कोई भी इन अभिन्नों की विश्लेषणात्मक रूप से गणना करने में सक्षम नहीं था, इसलिए उन्हें फिर से मानचित्रण का उपयोग करके संख्यात्मक रूप से गणना करना होगा (जैसा कि वे मूल प्रकाशनों में कहते हैं, आप ऐसा नहीं कर सकते!)।

संख्यात्मक एकीकरण

आकार और आलस्य के कारणों के लिए, हम इसे जितना संभव हो उतना बेवकूफ समझेंगे: $$$\ int_A ^ B f (x) dx \ लगभग \ frac {\ left | B - A \ right |} {N} \ sum_ {i = 0} ^ N f (A + i \ cdot \ frac {vec { बी - ए}} {एन})$

रे मार्चिंग को प्रकाश धारा के विपरीत दिशा में किया जाएगा: कैमरा बिंदु से $$$O$ ज्यामिति के साथ बीम के चौराहे से पहले $$$ब$ । रेखा खंड $$$ओ \ _ राइटरो बी$ द्वारा विभाजित किया गया $$$एन$ कदम दूर है।

मार्च शुरू करने से पहले, चर को आरंभ करें:

• vec2 (दो अलग घटक, रेले और एरोसोल बिखरने के लिए) कुल संचित ऑप्टिकल मोटाई $$$\ mathbf {T_ \ rho} (P (s) \ rightarrow O)$
• vec3 (RGB) $$$\ mathbf {I_M}$ । $$$\ mathbf {I_R}$

बिंदु के लिए अगला $$$P_i$ के बीच हर कदम $$$O$ और $$$ब$ :

1. चलो रे $$$\ vec {s}$ सूर्य की दिशा में और एक बिंदु प्राप्त करें $$$A_i$ वायुमंडल से इस किरण का बाहर निकलना।
2. मोटाई की गणना करें $$$\ mathbf {T} (A \ rightarrow P_i)$ पहले गणना करके $$$\ int_A ^ {P_i} \ rho_M (s) ds$ और $$$\ int_A ^ {P_i} \ rho_R (s) ds$ समान री-मार्चिंग (चरण M की संख्या के साथ) का उपयोग कर, और फिर परिणामी शब्दों को संबंधित स्थिरांक के साथ गुणा करें $$$\ beta_M ^ ई$ और $$$\ mathbf {\ beta_R ^ e}$ ।
3. मोटाई की गणना करें $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O) = \ mathbf {T_ \ rho} (P_ {i-1} \ rightarrow O) + \ rho_i (s) \ cdot ds$
4. संचित $$$\ mathbf {I_R}$ और $$$\ mathbf {I_M}$ इन मूल्यों का उपयोग करना

पुनरावर्तन के बाद अंतिम रंग की गणना शब्दों के योग से की जाती है:

1. रक़म $$$\ mathbf {L_ {BO}}$ तुच्छ हो जाओ: एक चर युक्त $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O)$ मान होता है $$$\ mathbf {T_ \ rho} (B \ rightarrow O)$ क्योंकि $$$P_i$ पहुंच गया है $$$ब$ ।
2. गुणा करके $$$\ mathbf {I_R}$ और $$$\ mathbf {I_M}$ संबंधित स्थिरांक और परिणाम जोड़कर गणना की जाती है $$$\ mathbf {L_ {in}}$

shaders

बिना किसी के साधारण बिखराव

थोड़े से कंघी और सीधे बिखरे हुए स्रोतों के बारे में टिप्पणी की (लगभग) सीधे इंट्रा से ही:

 const float R0 = 6360e3; //    const float Ra = 6380e3; //     const vec3 bR = vec3(58e-7, 135e-7, 331e-7); //    const vec3 bMs = vec3(2e-5); //    const vec3 bMe = bMs * 1.1; const float I = 10.; //   const vec3 C = vec3(0., -R0, 0.); //   ,  (0, 0, 0)    //   //  vec2(rho_rayleigh, rho_mie) vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); //    return vec2(exp(-h/8e3), exp(-h/12e2)); } //    ,        float escape(vec3 p, vec3 d, float R) { vec3 v = p - C; float b = dot(v, d); float det = b * b - dot(v, v) + R*R; if (det < 0.) return -1.; det = sqrt(det); float t1 = -b - det, t2 = -b + det; return (t1 >= 0.) ? t1 : t2; } //         `L`   `p`   `d` //   `steps`  //  vec2(depth_int_rayleigh, depth_int_mie) vec2 scatterDepthInt(vec3 o, vec3 d, float L, float steps) { vec2 depthRMs = vec2(0.); L /= steps; d *= L; for (float i = 0.; i < steps; ++i) depthRMs += densitiesRM(o + d * i); return depthRMs * L; } //   (  --   ) vec2 totalDepthRM; vec3 I_R, I_M; //    vec3 sundir; //    ,    `-d`   `L`   `o`   `d`. // `steps` --    void scatterIn(vec3 o, vec3 d, float L, float steps) { L /= steps; d *= L; //   O  B for (float i = 0.; i < steps; ++i) { // P_i vec3 p = o + d * i; vec2 dRM = densitiesRM(p) * L; //  T(P_i -> O) totalDepthRM += dRM; //     T(P_i ->O) + T(A -> P_i) // scatterDepthInt()    T(A -> P_i) vec2 depthRMsum = totalDepthRM + scatterDepthInt(p, sundir, escape(p, sundir, Ra), 4.); vec3 A = exp(-bR * depthRMsum.x - bMe * depthRMsum.y); I_R += A * dRM.x; I_M += A * dRM.y; } } //    // O = o --   // B = o + d * L --   // Lo --     B vec3 scatter(vec3 o, vec3 d, float L, vec3 Lo) { totalDepthRM = vec2(0.); I_R = I_M = vec3(0.); //  T(P -> O) and I_M and I_R scatterIn(o, d, L, 16.); // mu = cos(alpha) float mu = dot(d, sundir); //     return Lo * exp(-bR * totalDepthRM.x - bMe * totalDepthRM.y) //   + I * (1. + mu * mu) * ( I_R * bR * .0597 + I_M * bMs * .0196 / pow(1.58 - 1.52 * mu, 1.5)); } 

शडर पर चुप रहो

बादल

बुरा नहीं है, लेकिन इस तरह की तस्वीर को ग्रेडिएंट्स के कुछ चालाक ढेर के साथ बहुत आसान भी प्राप्त किया जा सकता है।

भ्रामक तरीके से, बादलों और भगवान की किरणों को प्राप्त करना अधिक कठिन है। चलो जोड़ते हैं।

यह विचार है कि एरोसोल के साथ बादलों को अनुमानित किया जाए और केवल घनत्व फ़ंक्शन densitiesRM() संशोधित किया जाए। यह शारीरिक रूप से सही नहीं हो सकता है जैसा हम चाहेंगे (मुझे नहीं पता कि कंप्यूटर ग्राफिक्स में बादलों में प्रकाश का प्रकीर्णन वास्तव में कैसे होता है)।

 //      const float low = 1e3, hi = 25e2; // vec4 noise24(vec2 v) --       // float t --  float noise31(vec3 v) { return (noise24(v.xz).x + noise24(v.yx).y) * .5; } vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); vec2 retRM = vec2(exp(-h/8e3), exp(-h/12e2) * 8.); //    () if (low < h && h < hi) { vec3 v = 15e-4 * (p + t * vec3(-90., 0., 80.)); //    <s></s>      :     retRM.y += 250. * step(vz, 38.) * smoothstep(low, low + 1e2, h) * smoothstep(hi, hi - 1e3, h) * smoothstep(.5, .55, //  :   .75 * noise31(v) + .125 * noise31(v*4. + t) + .0625 * noise31(v*9.) + .0625 * noise31(v*17.)-.1 ); } return retRM; } 

अपेक्षाओं के विपरीत, हमें सुंदर बादल, एक प्यारी जीत और प्रशंसक नहीं, बल्कि कलाकृतियां मिलती हैं। माथे पर कलाकृतियों की संख्या बढ़ाने की कोशिश पूरी तरह से नहीं हटाती है, लेकिन प्रदर्शन को काफी खराब करती है।

समाधान इंट्रा धक्का कि बैसाखी:

• क्षितिज पर सबसे अप्रिय कलाकृतियाँ पहाड़ों के पीछे छिपी हुई हैं
• बादल केवल कैमरे के पास जोड़े जाते हैं।
• मोंटे-कार्लोस्विना को जोड़ा जाता है, प्रत्येक मार्चिंग किरण को एक यादृच्छिक ऑफसेट द्वारा स्थानांतरित किया जाता है: के for (float i = pixel_random.w; i < steps; ++i) । यह बहुत शोर को जोड़ता है जो आपको लगातार फ्रेम को मिलाकर अस्थायी रूप से चिकना करना है।

• अधिक विवरण की आवश्यकता वाले क्षेत्रों के लिए चरणों की संख्या बढ़ रही है (उदाहरण के लिए, बादलों के साथ एक परत)। इसके लिए यह है कि इस तरह के बेतुके पृथक्करणों को scatterImpl() और scatterDepthInt() :

  
  

   //    scatterIn() vec2 depthRMsum = totalDepthRM; float l = max(0., escape(p, sundir, R0 + hi)); if (l > 0.) //   16  depthRMsum += scatterDepthInt(p, sundir, l, 16.); //     4- depthRMsum += scatterDepthInt(p + sundir * l, sundir, escape(p, sundir, Ra), 4.); 

  
  

   //   scatter() //  10    float l = 10e3; if (L < l) scatterIn(o, d, L, 16.); else { scatterIn(o, d, l, 32.); // 8  --     scatterIn(o+d*l, d, Ll, 8.); } 

  
  

दृश्य ज्यामिति के साथ संरेखण

दूरी और छाया कार्यों के पारंपरिक री-मैपिंग के परिणामस्वरूप, दूरी L से बिंदु B और पिक्सेल रंग Lo को पहले ही प्राप्त कर लिया गया है। इन मूल्यों को केवल scatter() फ़ंक्शन में प्रतिस्थापित किया जाता है। यदि बीम ज्यामिति के खिलाफ आराम नहीं करता है और दृश्य छोड़ देता है, तो रंग Lo शून्य है, और L गणना escape() का उपयोग करके L जाती है - यह माना जाता है कि बीम ने वातावरण को छोड़ दिया है।

सब कुछ पसंद है।

... वास्तव में, बिल्कुल नहीं। यह सभी भागों को एक साथ रगड़ने के लिए एक बड़ा दर्द है ताकि यह संपूर्ण रूप से विश्वसनीय लगे। बस घुमा मापदंडों, दृश्य ज्यामिति, शोर कार्यों, प्रक्षेपवक्र और कैमरा कोण के साथ उपद्रव का एक गुच्छा। मुझे डर है कि मेरे पास यहाँ अच्छी सलाह नहीं है, सिवाय कई घंटों के दौरान और दीवार के खिलाफ अपना सिर पीटने के अलावा।

minification

शेडर मिनिफायर को संसाधित करने के बाद, अंतिम शेडर स्कैटर कोड लगभग 1500 बाइट आकार में होता है। क्रिंकलर इसे ~ 700 बाइट्स तक संपीड़ित करता है, जो सभी shader कोड का लगभग 30% है।

प्रजनन

मुझे नहीं पता कि कंप्यूटर ग्राफिक्स कैसे हैं।