बहुपद प्रतिगमन मॉडल

सरल शब्दों में, गणितीय आंकड़ों में प्रतिगमन मॉडल ज्ञात आंकड़ों के आधार पर बनाया गया है, जो संख्याओं के जोड़े हैं। ऐसे जोड़ों की संख्या पूर्व निर्धारित है। यदि आप कल्पना करते हैं कि एक जोड़ी में पहला नंबर समन्वय का मूल्य है $$$x$ और दूसरा $$$य$ , तो अंकों के ऐसे सेट के रूप में कार्टेसियन समन्वय प्रणाली में संख्याओं के सेट को विमान पर दर्शाया जा सकता है। इन नंबरों के जोड़े को यादृच्छिक रूप से नहीं लिया जाता है। व्यवहार में, एक नियम के रूप में, दूसरी संख्या पहले पर निर्भर करती है। एक प्रतिगमन का निर्माण करने का मतलब है एक लाइन (अधिक सटीक रूप से, एक फ़ंक्शन) लेने के लिए जो उपरोक्त दृष्टिकोणों के बहुत करीब से संभव है (अनुमानित)।

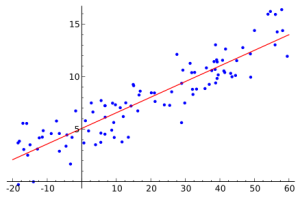
यह सब किस लिए है? सबसे पहले, यह तथाकथित की तैयारी के लिए आवश्यक है पूर्वानुमान। अक्सर पता लगाने की जरूरत है $$$य$ केवल जानना $$$x$ यदि यह उन एक्स से अलग है, जिसके आधार पर प्रतिगमन का निर्माण किया गया था। मैं एक सरल उदाहरण दूंगा। अध्ययन किए गए 100 अलग-अलग लोगों के आधार पर किसी व्यक्ति की उसकी उम्र की वृद्धि पर निर्भरता के आंकड़े हैं। इस प्रकार, हमारे पास 100 जोड़े संख्याएं हैं {आयु; विकास}। उसी समय, "विकास" एक निर्भर मात्रा है, और "आयु" स्वतंत्र है। एक प्रतिगमन मॉडल का सही ढंग से निर्माण करके, हम किसी भी आयु मूल्य द्वारा किसी भी निश्चितता के साथ विकास की "भविष्यवाणी" कर सकते हैं।

व्यवहार में, स्थिति के आधार पर, प्रतिगमन मॉडल के निर्माण में रैखिक, पैराबोलिक, शक्ति और अन्य प्रकार के कार्यों का उपयोग किया जाता है। गणितीय आँकड़ों के क्रम में, रैखिक प्रतिगमन मॉडल सबसे अधिक बार माना जाता है। कभी-कभी वे अधिक जटिल मामले को छूते हैं - एक परवलयिक मॉडल। एक सामान्यीकरण बनाना, यह अनुमान लगाना आसान है कि रैखिक और परवलयिक मॉडल एक अधिक जटिल मॉडल के विशेष मामले हैं - बहुपद। एक प्रतिगमन मॉडल बनाने का मतलब है कि इसमें दिखाई देने वाले फ़ंक्शन के मापदंडों को खोजना होगा। रैखिक प्रतिगमन के लिए - दो पैरामीटर: गुणांक और मुक्त शब्द।

बहुपद प्रतिगमन का उपयोग गणितीय आंकड़ों में समय श्रृंखला के प्रवृत्ति घटकों को मॉडल करने के लिए किया जा सकता है। एक समय श्रृंखला, वास्तव में, संख्याओं की एक श्रृंखला है जो समय पर निर्भर करती है। उदाहरण के लिए, पिछले एक साल के लिए औसत दैनिक तापमान, या कंपनी की मासिक आय। सिम्युलेटेड बहुपद के क्रम का मूल्यांकन विशेष विधियों द्वारा किया जाता है, उदाहरण के लिए, श्रृंखला की कसौटी पर। समय श्रृंखला के क्षेत्र में बहुपद प्रतिगमन के एक मॉडल के निर्माण का लक्ष्य अभी भी एक ही है - पूर्वानुमान।

शुरुआत करने के लिए, हम बहुपद प्रतिगमन की समस्या पर सामान्य तरीके से विचार करते हैं। सभी तर्क रैखिक और परवलयिक प्रतिगमन समस्याओं में तर्क के सामान्यीकरण पर आधारित है। इन विचारों के बाद, मैं एक विशेष मामले पर आगे बढ़ूंगा - समय श्रृंखला के लिए इस मॉडल पर विचार।

टिप्पणियों की दो श्रृंखला दी जाए $$$x_i$ (स्वतंत्र चर) और $$$y_i$ (आश्रित चर) $$$i = \ overline {1, n}$ । बहुपद समीकरण का रूप है

$$

$$y = \ sum \ limit_ {j = 0} ^ k b_jx ^ j, \ \ \ \ \ (1)$$

जहाँ $$$b_j$ - इस बहुपद का मानदंड, $$$j = \ overline {0, k}$ । उनमें से $$$b_0$ - एक मुक्त सदस्य। आइए हम सबसे कम वर्ग (OLS) पैरामीटर खोजें $$$b_j$ प्रतिगमन दिया गया।

रैखिक प्रतिगमन के साथ सादृश्य द्वारा, ओएलएस भी निम्नलिखित अभिव्यक्ति को कम करने पर आधारित है:

$$

$$S = \ sum \ limit_ {i = 1} ^ n \ left (\ hat y_i-y_i \ right) ^ 2 \ to \ min \ \ \ \ (2)$$

यहां $$$\ _ y_i$ - सैद्धांतिक मूल्य जो बिंदुओं पर बहुपद (1) के मान हैं $$$x_i$ । प्रतिस्थापन (1) में (2), हम प्राप्त करते हैं

$$

$$S = \ sum \ limit_ {i = 1} ^ n \ left (\ sum_ {j = 0} ^ kb_jx_i ^ j-y_i \ right) ^ 2 \ _ to मिनट$$

फ़ंक्शन के चरम पर आवश्यक स्थिति के आधार पर $$$(k + 1)$ चर $$$S = S (b_0, b_1, \ dots, b_k)$ हम इसके आंशिक व्युत्पन्न को शून्य के बराबर करते हैं, अर्थात

$$

$$S '_ {b_p} = 2 \ sum \ limit_ {i = 1} ^ nx_i ^ p \ left (\ sum \ limit_ {j = 0} ^ kb_jx_i ^ j-y_i's दाईं ओर = 0, \ \ p) = \ overline {0, k}।$$

प्रत्येक समानता के बाएँ और दाएँ पक्षों को 2 से विभाजित करने पर, हम दूसरी राशि को प्रकट करते हैं:

$$

$$\ _ \ _ सीमाएं {{1 = 1} ^ nx_i ^ p \ left (b_0 + b_1x_i + b_2x_i ^ 2 + \ dots + b_kx_i ^ k \ दाएँ) - n \ _ सीमा = {i = 1} ^ nx_i ^ py_i = 0 , \ \ \ पी = \ ओवरलाइन {0, के}।$$

कोष्ठक खोलना, हम प्रत्येक में स्थानांतरित करते हैं $$$पी$ वें अभिव्यक्ति, के साथ अंतिम शब्द $$$y_i$ दाईं ओर और दोनों पक्षों को विभाजित करें $$$एन$ । नतीजतन, हम मिल गए $$$(k + 1)$ के लिए रेखीय सामान्य समीकरणों की एक प्रणाली बनाने वाले भाव $$$b_p$ । इसका निम्न रूप है:

$$

$$\ बाईं \ {\ _ शुरू करें {सरणी} {l} b_0 + b_1 \ overline x + b_2 \ overline {x ^ 2} + \ dots + b_k \ overline {x ^ k} = \ overline yidy b_0 \ overline x + b_1 \ overline {x ^ 2} + b_2 \ overline {x ^ 3} + \ dots + b_k \ overline {x ^ {k + 1}} = \ overline {xy} \\ b_0 \ _line {x ^ 2} + b_1 \ overline {x ^ 3} + b_2 \ overline {x ^ 4} + \ dots + b_k \ overline {x ^ {k + 2}} = \ overline {x ^ 2y} \\ \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \\ b_0 \ overline {x ^ k} + b_1 ओवरलाइन {x ^ {k + 1}} + b_2 \ overline {x ^ x {k + 2}} + \ dots + b_k \ overline {x ^ {2k}} = \ overline {x ^ ky} \ end {सरणी} \ right। \ \ \ \ \ (3)$$

आप मैट्रिक्स रूप में सिस्टम (3) को फिर से लिख सकते हैं: $$$AB = C$ जहाँ

$$

$$A = \ left (\ start {array} {ccccc} 1 & \ overline x & \ overline {x ^ 2} & \ ldots & \ overline {x ^ k} \\ \ overline x & \ _ xline # 2 ^ } & \ overline {x ^ 3} & \ ldots & \ overline {x ^ {k + 1}} \\ \ overline {x ^ 2} और \ overline {x ^ 3} & \ overline {x ^ 4} & \ ldots & \ overline {x ^ {k + 2}} \\ \ vdots & \ vdots & \ vdots & \ ddots & \ vdots \\ \ overline {x ^ k} & \ overline {x ^ {k + 1} } & \ overline {x ^ {k + 2}} & \ ldots & \ overline {x ^ {2k}} \ end {सरणी} \ right), \ \ B = \ बाएँ (\ शुरू {सरणी} {c} b_0 \\ b_1 \\ b_2 \\\ vdots \\ b_k \ end {array} \ right), \ \ C = \ left (\ start {array} {c} \ overline y \\\ "xy} \\) को ओवरलाइन करें \ overline {x ^ 2y} \\\ vdots \\\ ओवरलाइन {x ^ ky} \ end {सरणी} \ right) $$$

अब हम समय श्रृंखला के मामले में उपरोक्त तथ्यों के आवेदन की ओर मुड़ते हैं। समय श्रृंखला दें $$$x_t$ जहाँ $$$t = \ overline {1, n}$ । एक बहुपद आदेश प्रवृत्ति का निर्माण करना आवश्यक है $$$k$ , जो दी गई समय श्रृंखला को यथासंभव सटीक रूप से अनुमानित करता है। एक स्वतंत्र चर के रूप में $$$x$ हम लेंगे $$$टी$ एक समय श्रृंखला की परिभाषा के आधार पर। ये एक्स प्राकृतिक समय की एक श्रृंखला है जो समय की अवधि को दर्शाते हैं। एक के रूप में $$$य$ समय श्रृंखला मान लिया जाता है $$$x_t$ । यह देखा जा सकता है कि तत्वों के मूल्य $$$a_ {ij}$ सिस्टम मैट्रिसेस $$$ए$ से स्वतंत्र $$$x_t$ । चूंकि सामान्य मामले में, स्पष्ट रूप से,

$$

$$a_ {ij} = \ overline {x ^ {i + j-2}} = \ frac1n \ sum \ limit_ {r = 1} ^ nx_r ^ {i + j-2},$$

फिर समय श्रृंखला के मामले में

$$

$$a_ {ij} = \ frac1n \ sum \ limit_ {r = 1} ^ nr ^ {i + j-2},$$

जहाँ $$$i, j = \ overline {1, (k + 1)}$

तत्वों $$$c_j$ मुक्त शर्तों के मैट्रिक्स वैक्टर $$$सी$ आम तौर पर प्राप्त के रूप में

$$

$$c_j = \ overline {x ^ {j-1} y} = \ frac1n \ sum \ limit_ {r = 1} ^ nx_r ^ {j-1} y_r।$$

और समय श्रृंखला के मामले में

$$

$$c_j = \ frac1n \ sum \ limit_ {r = 1} ^ nr ^ {j-1} x_j,$$

जहाँ $$$j = \ overline {1, (k + 1)}।$

इस प्रकार, समाधान प्रणाली (3) होने से, हम बहुपद प्रवृत्ति के वांछित मापदंडों को पा सकते हैं $$$b_0, \ dots, b_k।$

सिस्टम के मेट्रिसेस में भरने के लिए और इसे हल करने के लिए, संख्यात्मक विधियों में से एक का उपयोग कंप्यूटर पर एक प्रवृत्ति मॉडलिंग करते समय किया जा सकता है। इस मामले में, गणना परिणाम काफी सटीक होगा।

नतीजतन, प्रवृत्ति घटक फार्म ले जाएगा:

$$

$$T_t = \ sum \ limit_ {i = 0} ^ kb_it ^ i, \ \ \ t = 0,1,2, \ dots।$$

यह भी ध्यान देने योग्य है कि नकली प्रवृत्ति घटक $$$T_t$ , न केवल वर्तमान अवधि के लिए निर्धारित किया जाता है $$$[1; एन]$ , लेकिन भविष्य की अवधि के लिए भी $$$t> n$ ।

मैं इस बात पर ध्यान देता हूं कि बहुपद प्रतिगमन मॉडल केवल समय श्रृंखला के प्रवृत्ति घटक हैं। एक पूर्ण समय श्रृंखला मॉडल भी अन्य घटकों का अर्थ है, जो इस लेख के दायरे से परे है।

व्यवहार में, मैंने व्यक्तिगत रूप से 2 से अधिक के बहुपद प्रवृत्ति क्रम के साथ समय श्रृंखला नहीं देखी है। यह बहुपद के विशेष मामलों के रूप में रैखिक और प्रबोलिक प्रतिगमन मॉडल के प्रसार की व्याख्या करता है।