🕴🏿 👨‍🔧 🎊 सूचना-मापन चैनल में IIR फ़िल्टर का सॉफ्टवेयर कार्यान्वयन 👨🏽‍⚖️ 👩🏼‍🤝‍👩🏻 🤫

पर्यावरण की स्थिति के बारे में जानकारी या, उदाहरण के लिए, पर्यावरण या वस्तु के कुछ गुणों को चिह्नित करने वाले मापदंडों के वर्तमान मूल्यों को मापकर एक निश्चित नियंत्रण वस्तु प्राप्त की जा सकती है। तकनीकी साधनों द्वारा ऐसी जानकारी प्राप्त करने, संसाधित करने और संचारित करने के लिए, मापा मापक का मान सूचना मापने के संकेत में स्वचालित माप उपकरणों द्वारा परिवर्तित किया जाना चाहिए। ऐसा करने के लिए, सूचना-मापने वाले चैनल ( IIC ) को तकनीकी साधनों के संयोजन के रूप में लागू करें, जिनमें से प्रत्येक अपने विशिष्ट कार्य को पूरा करेगा, मापा मूल्य की धारणा से शुरू होता है और मापने की जानकारी की प्राप्ति के साथ समाप्त होता है, जो मानव धारणा के लिए सुविधाजनक रूप में या इसके आगे के प्रसंस्करण के लिए सुविधाजनक है। और सब कुछ ठीक होगा, लेकिन जानकारी के मार्ग के साथ, हस्तक्षेप ई (टी) माप सूचना के उपयोगी संकेत y (टी) पर आरोपित है - समय का एक यादृच्छिक कार्य जो मापने वाले ट्रांसड्यूसर की यादृच्छिक त्रुटि, कनेक्टिंग तारों में बिजली के पिकअप और यादृच्छिक तरंगों का अनुकरण कर सकता है। मापा पैरामीटर, और अन्य कारक।

इसके आधार पर, समस्या आईआईसी में सूचना के प्राथमिक प्रसंस्करण में उत्पन्न होती है - यादृच्छिक हस्तक्षेप ई (टी) से माप सूचना के संकेत y (टी) को फ़िल्टर करना। मूल रूप से, फ़िल्टरिंग पद्धतियाँ y (t) और e (t) के फ़्रीक्वेंसी स्पेक्ट्रा के अंतर पर आधारित होती हैं, और हस्तक्षेप को अधिक उच्च-आवृत्ति माना जाता है।

कार्यान्वित इष्टतम फिल्टर का संश्लेषण एक जटिल कार्य है, जिसके समाधान के लिए उपयोगी संकेत और हस्तक्षेप की विशेषताओं के सटीक विनिर्देश की आवश्यकता होती है। इसलिए, व्यवहार में, फ़िल्टर के हस्तांतरण समारोह को आमतौर पर सरल फ़िल्टरिंग एल्गोरिदम का उपयोग करके पैरामीट्रिक संश्लेषण तक सीमित और सीमित किया जाता है।

निस्पंदन विधियों को सॉफ्टवेयर स्तर और हार्डवेयर स्तर दोनों पर किया जाता है। उदाहरण के लिए, BMP280 (बॉश) सेंसर में, हार्डवेयर स्तर पर IIR फ़िल्टर कनेक्ट करना संभव है, यदि आवश्यक हो, तो फ़िल्टर गुणांक k को बदलना, [1]।

IIR फ़िल्टर

अनंत आवेग प्रतिक्रिया के साथ फिल्टर पुनरावर्ती फिल्टर होते हैं और पिछले इनपुट और आउटपुट नमूनों के मूल्यों के आधार पर आउटपुट सिग्नल की गणना करते हैं। सैद्धांतिक रूप से, एक IIR फ़िल्टर की आवेग प्रतिक्रिया कभी शून्य तक नहीं पहुंचती है, इसलिए आउटपुट अवधि में अनंत है।

सामान्य तौर पर, हम एक आयामी स्केलर डिजिटल फ़िल्टर को फ़िल्टर करने के लिए एल्गोरिथ्म लिखते हैं: [२]

y [n] = T (x [n], x [n - १], . . ., x [n - M], y [n - १], . . ., y [n - N], n)

$y [n] = T (x [n], x [n-१], ..., x [n-M], y [n-१], ..., y [n-N], n)$ , (1),
जहाँ T एक चर का एक अदिश कार्य है।

फ़ंक्शन T वर्तमान इनपुट सिग्नल x [n] पर निर्भर करता है, और पिछले: इनपुट सिग्नल के एम नमूने

और आउटपुट सिग्नल के एन नमूने

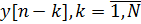
IIR फ़िल्टर का आउटपुट फॉर्म के अंतर समीकरण द्वारा वर्णित है:

(2)
जहाँ x [n], y [n] क्रमशः फ़िल्टर, का इनपुट और आउटपुट है, {

a_{k}

${a_k}$ } सीधा गुणांक का समूह है, M प्रत्यक्ष गुणांक की संख्या है, {

b_{k}

${b_k}$ } उलटा गुणांक का एक सेट है, एन उलटा गुणांक की संख्या है।

समीकरण (2) के दोनों पक्षों में z- परिवर्तन लागू करते हुए, हम प्राप्त करते हैं:

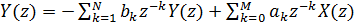
(3)।

तब फ़िल्टर का स्थानांतरण कार्य इस तरह दिखाई देगा:

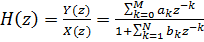
(4)

एक आयामी IIR फ़िल्टर को फ़िल्टर करने के लिए एल्गोरिथम

सामान्य शब्दों में, एक आयामी स्केलर स्थिर पुनरावर्ती फ़िल्टर के लिए फ़िल्टरिंग एल्गोरिथ्म इस तरह दिखता है:

y [n] = T (x [n], y [n - 1])

$y [n] = T (x [n], y [n-1])$ । (5)

अब हम फॉर्म में IIR फ़िल्टर के लिए अंतर समीकरण लिखते हैं:

(6)
जहां फ़िल्टर फिल्टर गुणांक है;
या

y [n] = a y [n - 1] + b x [n]

$y [n] = ay [n-1] + bx [n]$ (7)
जहाँ

क्रमशः उलटा और आगे फिल्टर गुणांक हैं।

से (7) यह स्पष्ट है कि k = 1 पर फिल्टर का आउटपुट सिग्नल इनपुट को दोहराएगा, और जैसे ही फ़िल्टर गुणांक k बढ़ता है, पिछले फ़िल्टर किए गए सिग्नल का वजन 1 हो जाता है, और मापा मूल्य का वजन 0 हो जाता है।

एल्गोरिथम (6) को BMP280 सेंसर के लिए निरपेक्ष वायुमंडलीय दबाव सूचना-मापने वाले चैनल के उदाहरण के रूप में लागू किया गया है, Arduino Software (IDE) विकास पर्यावरण में सॉफ्टवेयर स्तर पर, लिस्टिंग 1. II घटकों के विद्युत कनेक्शन आरेख को अंजीर में दिखाया गया है। 1. प्रोटोटाइप IIC पूर्ण वायुमंडलीय दबाव का सामान्य दृश्य अंजीर में प्रस्तुत किया गया है। 2. प्रोटोटाइप, पोटेंशियोमीटर के नॉब को घुमाकर, 1 की 50 वृद्धि में 1 ... की रेंज में फिल्टर गुणांक को बदलने की क्षमता प्रदान करता है। लिक्विड क्रिस्टल डिस्प्ले का संकेत मापा दबाव मान (k = 1 के लिए) या फ़िल्टर किए गए मान (k = 2 ... 50 के लिए) और फ़िल्टर गुणांक k दिखाता है।

लिस्टिंग 1

//    () // -  - //https://github.com/orgua/iLib/blob/master/src/i2c.h #include "i2c.h" //https://github.com/orgua/iLib/blob/master/src/i2c_BMP280.h #include "i2c_BMP280.h" //https://github.com/arduino-libraries/LiquidCrystal #include <LiquidCrystal.h> //https://github.com/orgua/iLib/tree/master/examples/i2c_BMP280 BMP280 bmp280; const int rs = 12, en = 11, d4 = 6, d5 = 5, d6 = 4, d7 = 3; //const int rs = PB4, en = PB3, d4 = PD6, d5 = PD5, d6 = PD4, d7 = PD3; LiquidCrystal lcd(rs, en, d4, d5, d6, d7); float pascal_f = 100500; float filter_K = 1; const int analogInPin = A0; //    int sensorValue = 0; //   int outputValue = 0; void setup() { Serial.begin(9600); //Serial.print("Probe BMP280: "); if (bmp280.initialize()) { //Serial.println("Sensor found"); ; } else { Serial.println("Sensor missing"); while (1) {} } bmp280.setEnabled(0); bmp280.triggerMeasurement(); bmp280.setFilterRatio(0); lcd.begin(16, 2); lcd.setCursor(0, 0); lcd.print("measure"); lcd.setCursor(7, 1); lcd.print("Pa"); lcd.setCursor(10, 0); lcd.print("filter"); } void loop() { float temperature; float pascal, hpascal; sensorValue = analogRead(analogInPin); outputValue = map(sensorValue, 0, 1023, 1, 50); filter_K = outputValue; bmp280.awaitMeasurement(); bmp280.getTemperature(temperature); temperature -= 1.7; // bmp280.getPressure(pascal); pascal -= 50;// hpascal = pascal/100.; bmp280.triggerMeasurement(); pascal_f = (pascal_f * (filter_K - 1) + pascal) / filter_K; //(6) Serial.println(pascal_f,0); if(pascal_f < 100000) lcd.setCursor(6, 1); lcd.print(" "); lcd.setCursor(0, 1); lcd.print(pascal_f,0); if(filter_K < 10) lcd.setCursor(13, 1); lcd.print(" "); lcd.setCursor(10, 1); lcd.print(filter_K,1); delay(300); }

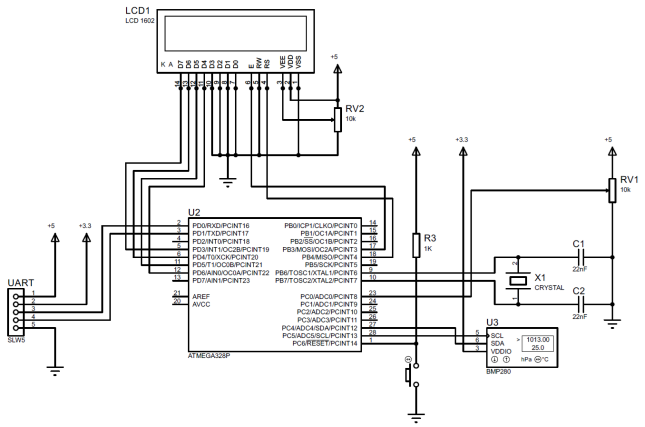अंजीर। 1 - प्रोटोटाइप IIC के घटकों के तारों आरेख

अंजीर। 2 - प्रोटोटाइप IIC का सामान्य दृश्य

IIR फिल्टर के शोध के लिए पायथन लिपि

IIR फ़िल्टर की जांच के लिए लिस्टिंग 2 एक पायथन स्क्रिप्ट दिखाता है। फ़िल्टर गुणांक k को स्क्रिप्ट में लिखा गया है। मापा दबाव मूल्यों को क्रमिक रूप से वर्चुअल COM पोर्ट से पढ़ा जाता है और फ़िल्टर किया जाता है। वास्तविक समय में मापा पैरामीटर के मापा और फ़िल्टर किए गए मान ग्राफिक विंडो में और कंसोल पर प्रदर्शित किए जाते हैं। प्रयोग के परिणाम तालिका में एक फ़ाइल द्वारा दर्ज किए जाते हैं, और ग्राफिक्स विंडो में मापा और फ़िल्टर किए गए मानों की समय सीमाएं प्रदर्शित की जाती हैं।

लिस्टिंग 2

 import numpy as np import matplotlib.pyplot as plt import serial from drawnow import drawnow import datetime, time k = 6.0 #  + 1 filter_K = 1 + k #     def cur_graf(): plt.title("BMP280") plt.ylim( 100450, 100510 ) plt.plot(nw, lw1, "r.-", label='') plt.plot(nw, lw1f, "b.-", label='') plt.legend(loc='best') plt.ylabel(r'$, $') plt.xlabel(r'$ \ $') plt.grid(True) #      def all_graf(): plt.close() fig=plt.figure() ax = fig.add_subplot(111) fig.subplots_adjust(top=0.85) ax.set_title(" BMP280\n" + str(count_v) + "-  " + "(" + now.strftime("%d-%m-%Y %H:%M") + ")") ax.set_ylabel(r'$, $') ax.set_xlabel(r'$ \ $' + '; (  : {:.6f}, c)'.format(Ts)) ax.text(0.95, 0.03, " : " + str(filter_K) + "\n", verticalalignment='bottom', horizontalalignment='right', transform=ax.transAxes, color='black', fontsize=14) plt.plot( n, l1, "r-", label='') plt.plot( n, l1f, "b-", label='') plt.legend(loc='best') plt.grid(True) plt.show() #   #    str_m = input("  : ") m = eval(str_m) #    mw = 16 #    ser = serial.Serial() ser.baudrate = 9600 port_num = input("   : ") ser.port = 'COM' + port_num ser #   try: ser.open() ser.is_open print(" : " + ser.portstr) except serial.SerialException: print("   : " + ser.portstr) raise SystemExit(1) #  l1 = [] #    l1f = [] #     t1 = [] #     lw1 = [] #     lw1f= [] #      n = [] #     nw = [] #      #      filename = 'count.txt' in_file = open(filename,"r") count = in_file.read() count_v = eval(count) + 1 in_file.close() in_file = open(filename,"w") count = str(count_v) in_file.write(count) in_file.close() filename = count + '_' + filename out_file = open(filename,"w") #      print("\n:\n") print("n -  ;") print("P - , ;") print("\n   \n") print('{0}{1}\n'.format('n'.rjust(4),'P'.rjust(10))) #     #  #   #       i = 0 while i < m: n.append(i) nw.append(n[i]) if i >= mw: nw.pop(0) line1 = ser.readline().decode('utf-8')[:-2] t1.append(time.time()) if line1: l1.append(eval(line1)) lw1.append(l1[i]) if i : l1f.append( (l1f[i-1]*(filter_K - 1) + l1[i])/filter_K ) #(6) lw1f.append(l1f[i]) else : l1f.append(l1[i]) lw1f.append(l1f[i]) if i >= mw: lw1.pop(0) lw1f.pop(0) print('{0:4d} {1:10.2f} {2:10.2f}'.format(n[i],l1[i],l1f[i]) ) drawnow(cur_graf) i += 1 #   ser.close() ser.is_open time_tm = t1[m - 1] - t1[0] print("\n  : {0:.3f}, c".format(time_tm)) Ts = time_tm / (m - 1) print("\n  : {0:.6f}, c".format(Ts)) #    print("\n    {}\n".format(filename)) for i in np.arange(0,len(n),1): count = str(n[i]) + "\t" + str(l1[i]) + "\n" out_file.write(count) #    out_file.close() out_file.closed #    now = datetime.datetime.now() #     all_graf() end = input("\n Ctrl-C,   ")

प्रयोग के परिणाम

   : 33    : 6  : COM6 : n -  ; P - , ;     n P 0 100490.00 100490.00 1 100488.00 100489.71 2 100487.00 100489.33 3 100488.00 100489.14 4 100488.00 100488.97 … 30 100486.00 100488.14 31 100492.00 100488.70 32 100489.00 100488.74   : 16.028, c   : 0.500875, c     275_count.txt  Ctrl-C,

निष्कर्ष

उपरोक्त फ़िल्टरिंग एल्गोरिथ्म सॉफ्टवेयर कार्यान्वयन में बहुत सरल है और व्यवहार में, इस लेख में चर्चा किए गए लोगों के समान IIC में उपयोग किया जा सकता है।
लालीखिन डी.ए., एस.वी. विभाग। CITYM ।

सूचना-मापन चैनल में IIR फ़िल्टर का सॉफ्टवेयर कार्यान्वयन

IIR फ़िल्टर

एक आयामी IIR फ़िल्टर को फ़िल्टर करने के लिए एल्गोरिथम

IIR फिल्टर के शोध के लिए पायथन लिपि

प्रयोग के परिणाम

निष्कर्ष

जानकारी के स्रोत

More articles: