🏇 🙇🏼 🧙🏼 एक विमान की ऊर्ध्वाधर उड़ान की गतिशीलता हवा की तुलना में हल्की होती है 🧑‍🤝‍🧑 😰 ↔️

परिचय

वायु (एलएएलवी) की तुलना में विमान के लाइटर और चढ़ाई की गति को निर्धारित करना लगभग एक महत्वपूर्ण कार्य है जो इस तरह के उपकरणों के डिजाइन में उत्पन्न होता है।

उदाहरण के लिए, बड़ी संख्या में एलएएलएफ के लिए समर्पित हैं, उदाहरण के लिए, हमारे संसाधन पर केवल दो बहुत ही दिलचस्प लेख हैं [1,2] विकास इतिहास से संबंधित उदाहरणों के रूप में एयरशिप और स्ट्रैटोस्टैट्स के विशिष्ट डिजाइन का उपयोग करते हुए। हालांकि, ऐसे उपकरणों की ऊर्ध्वाधर उड़ान की गतिशीलता की बहुत कम गणनाएं हैं, जो कम से कम मोटे तौर पर एसएलडब्ल्यू की चढ़ाई और वंश की गति का निर्धारण करते हैं।

अंतिम विवरण के लिए एक निश्चित स्पष्टीकरण की आवश्यकता होती है, क्योंकि एक अनुभवी पाठक को स्कूल भौतिकी पाठ्यक्रम याद है, जिसमें वृद्धि की ऊंचाई पर समस्याएं और गुब्बारे के अन्य मापदंडों को हवा की तुलना में गैसों से भरा हुआ या हवा से उड़ान के दौरान ही गर्म किया गया था।

ये सभी कार्य दो बलों की समानता पर आधारित थे: भार और बल की शक्ति। गैसों को आदर्श माना जाता था और उनके मापदंडों की गणना मेंडेलीव क्लैप्रोन के कानून के अनुसार की जाती थी। हालांकि, वायु प्रतिरोध की तीसरी ताकत की एक साधारण गणना पहले से ही अंतर समीकरणों की एक प्रणाली की ओर ले जाती है, जिसे विश्लेषणात्मक रूप से हल नहीं किया जा सकता है। वृद्धि और तापमान की ऊंचाई के साथ वायुमंडलीय हवा के घनत्व में परिवर्तन को ध्यान में रखना भी आवश्यक है।

इसके अलावा, यदि आपको न केवल वृद्धि पर विचार करने की आवश्यकता है, बल्कि गेंद की ठंड और जमीन पर इसके वंश भी हैं, तो यह बच्चों के कार्य में बिल्कुल नहीं है। मुझे उम्मीद है कि पायथन के माध्यम से एक समान समस्या के समाधान पर विचार करने से न केवल भौतिकी में ज्ञान के विस्तार में योगदान होगा, बल्कि खुद प्रोग्रामिंग भाषा पायथन का लोकप्रियकरण भी होगा। मैं इस संसाधन पर अपने प्रकाशनों में क्या करने की कोशिश करता हूं।

एक गेंद के आकार में एक खोल के साथ LALV की उड़ान का एक गणितीय मॉडल, जिसकी मात्रा ऊंचाई के साथ नहीं बदलती है

हम निम्नलिखित बलों की कार्रवाई के तहत अपने द्रव्यमान के केंद्र की गति पर विचार करने के लिए खुद को प्रतिबंधित करते हैं: गुरुत्वाकर्षण ( जी ), आर्किमिडीयन बल ( एफए ) और वायुगतिकीय खींचें बल ( एफसी )। हम गति और वायु पर्यावरण के मापदंडों के माध्यम से बलों को निर्धारित करने के लिए संबंध लिखते हैं [3]:

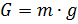
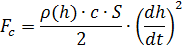
उपरोक्त सूत्रों में, संकेतन का उपयोग किया जाता है: h गेंद की ऊँचाई है, dh / dt ऊर्ध्वाधर गति है, m द्रव्यमान है, g गुरुत्वाकर्षण का त्वरण है, W गेंद का आयतन है, c खींचें गुणांक है, S विशेषता प्रतिरोध क्षेत्र (midship area) है।
ऊंचाई पर वायु घनत्व की निर्भरता को घातांक माना जाएगा:

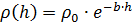
जहाँ

ρ_{0}

$ρ_0$ - शून्य ऊंचाई पर वायु घनत्व, बी - गुणांक। गुरुत्वाकर्षण को नीचे की ओर निर्देशित किया जाता है, आर्किमिडीयन बल को ऊपर की ओर निर्देशित किया जाता है, और वायुगतिकीय खींचें के बल को हमेशा "गति के विरुद्ध" निर्देशित किया जाता है, इसलिए गति के समीकरणों में इस बल के सही समावेश के लिए एक कारक की आवश्यकता होती है।

- स ि ं ग (d h / d t)

$-सिंग (dh / dt)$ ।

हालांकि, हमारे उद्देश्यों के लिए यह तथ्य मौलिक महत्व का नहीं है, और हम गेंद को उठाने के केवल चरण पर विचार करने के लिए खुद को सीमित करते हैं, जब वायुगतिकीय ड्रैग फोर्स को नीचे की ओर निर्देशित किया जाता है और इसलिए, माइनस साइन के साथ गति के समीकरणों को ध्यान में रखा जाएगा। अब गति के समीकरण को इस प्रकार लिखा जा सकता है:

, (1)

इसके अतिरिक्त, मान लें कि गुब्बारा घनत्व के साथ त्रिज्या R का एक सजातीय शरीर है

ρ_{b}

$ρ_b$ । फिर इसके एरोडायनामिक ड्रैग को निर्धारित करने वाले क्षेत्र के आकार को परिभाषित किया गया है

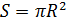
मात्रा के रूप में

, और द्रव्यमान, क्रमशः, के रूप में

।

अब यह स्पष्ट है कि समीकरण के प्रत्येक शब्द (1) में एक कारक के रूप में एस शामिल है। इसलिए, समीकरण के समीकरण के प्रत्येक शब्द को एस के एक कारक द्वारा कम किया जा सकता है। समीकरण स्वयं ही फॉर्म लेगा:

, (2)

हम निम्नलिखित संकेतन प्रस्तुत करते हैं:

;

;

और फिर से लिखना (2) nonlinear समीकरणों की निम्न प्रणाली के रूप में:

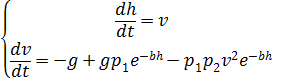
, (3)

LALV हवा के तापमान के बढ़ने की गति और ऊंचाई पर प्रभाव

ऐसा करने के लिए, हम पहले तापमान के बिना ऊंचाई पर वायुमंडलीय हवा के घनत्व की निर्भरता के लिए निम्नलिखित संबंध का उपयोग करके प्रणाली (3) को हल करते हैं:

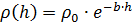
आइए हम सिस्टम के समाधान को दोहराते हैं (3), लेकिन ऊंचाई और तापमान पर वायु घनत्व की निर्भरता के संबंध का उपयोग करते हुए:

जहाँ: b = 0.000125 1 / m के वायु घनत्व के साथ जुड़ा एक स्थिर है;
A = 0.0065 K / m में हवा के तापमान से संबंधित एक स्थिर है।

T_{0} = 300 K

$T_0 = 300 K$ - समुद्र तल पर तापमान।

कार्यक्रम सूचीकरण

# -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. R=8#     . b=0.000125# ,      1/ a=6.5*10**-3# ,      / c=0.4#   mo=240#   V=(4/3)*pi*R**3 rs=rg+mo/V#    ,  ,   p1=rv/rs#   p2=3*c/(8*R)#   T0=300 def fun(y, t): y1, y2= y return [y2,-g+g*p1*exp(-b*y1*T0/(T0-a*y1))-p1*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] t =arange(0,1100,0.01) y0 = [0.0,0.0] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.title("   \n : %s 3.  : %s . \n  : %s k. "%(round(V,0),mo,round(0.001*g*rv*V,0))) plt.plot(t/60,y1,label='  : %s . \n  : % s / .\n    '%(round(max(y1)/1000,2),round(max(y2),2))) def fun(y, t): y1, y2= y return [y2,-g+g*p1*exp(-b*y1)-p1*p2*exp(-b*y1)*y2**2] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.plot(t/60,y1,label='  : %s . \n  : % s / \n    '%(round(max(y1)/1000,2),round(max(y2),2))) plt.ylabel('  ') plt.xlabel('   ') plt.legend(loc='best') plt.grid(True) plt.show()

हमें मिलता है:

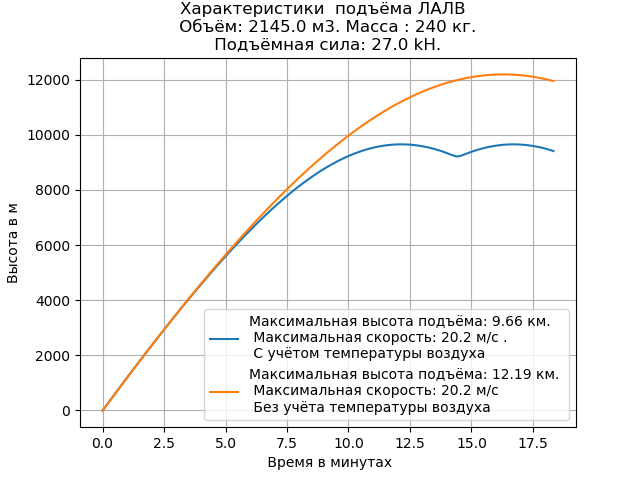
तापमान को ध्यान में रखते हुए, LALV लिफ्ट की ऊंचाई की गणना मूल्य बिना से कम है। उपकरण की उठाने की गति अपरिवर्तित रहती है।

शुरू से लैंडिंग तक एसएएलवी उड़ान के सभी चरणों की विशेषताओं का निर्धारण

उड़ान कार्यक्रम का निर्माण करने के लिए LALV निम्नलिखित समय अवधि के लिए परिस्थितियों पर विचार करें:

उदय -

;
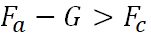
लटका -

;
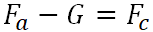
लैंडिंग -

।

कार्यक्रम सूचीकरण

 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. R=8#     . b=0.000125# ,      1/ a=6.5*10**-3# ,      / c=0.4#    mo=240#    V=(4/3)*pi*R**3 p2=3*c/(8*R)#   T0=300#     tz=4000#     rgu=1.2#         /3 tz=4000#   def fun(y, t): y1,y2= y if y2<=0: if t<tz: return [y2,-g+g*(rv/(rg+mo/V))*exp(-b*y1*T0/(T0-a*y1))+(rv/(rg+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] elif t>=tz: return [y2,-g+g*(rv/(rgu+mo/V))*exp(-b*y1*T0/(T0-a*y1))+(rv/(rgu+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] else: return [y2,-g+g*(rv/(rg+mo/V))*exp(-b*y1*T0/(T0-a*y1))-(rv/(rg+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] t =arange(0,tz+555,0.1) y0 = [0.0,0.0] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.title(", ,   \n      \n : %s 3.  : %s .  : %s k. "%(round(V,0),mo,round(0.001*g*rv*V,0))) plt.plot(t,y1,label='  : %s . \n  : % s / .\n   %s .'%(round(max(y1)/1000,2), round(max(y2),2),tz-2*555)) plt.ylabel('  ') plt.xlabel('   .') plt.legend(loc='best') plt.grid(True) plt.show()

हमें मिलता है:

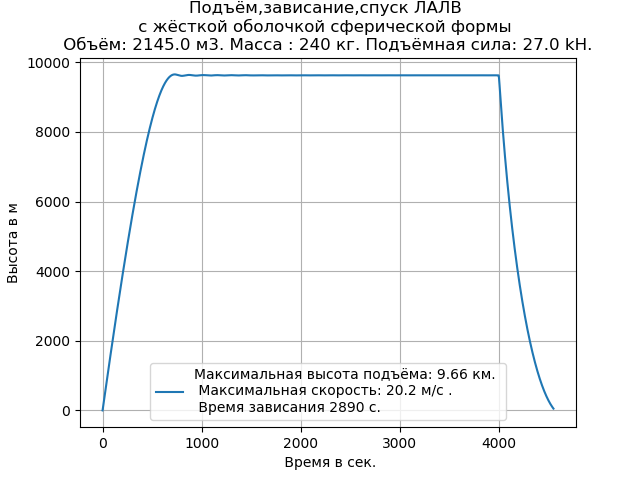
जैसा कि कम्प्यूटेशनल प्रयोग करने के लिए कार्यक्रम के ग्राफ और लिस्टिंग से किया गया है, यह आवश्यक प्रारंभिक डेटा दर्ज करने के लिए पर्याप्त है।

शेल के साथ एलएएलवी की उड़ान का एक गणितीय मॉडल, जिसकी मात्रा ऊंचाई के साथ बदलती है

ऐसे LALV में स्ट्रैटोस्टैट्स शामिल हैं। समताप मंडल का गुब्बारा पूरी तरह से हीलियम से फुलाया नहीं जा सकता है, जिससे इसे अधिकतम उठाने की शक्ति मिलती है, जो इसके गोले के आकार को गेंद में बदल देगा। आंतरिक और बाहरी दबाव में अंतर के कारण उच्च ऊंचाई पर ऐसी गेंद फट सकती है।

इन कारणों के लिए, अधिकतम प्राप्य लिफ्ट ऊंचाई की गणना के लिए, इसकी मात्रा के दो मूल्य पेश किए गए हैं: न्यूनतम विमिन और अधिकतम Vmax, क्रमशः। शुरू किए गए चर और ऊंचाई पर वायु घनत्व की निर्भरता को ध्यान में रखते हुए, उछाल बल और गुरुत्वाकर्षण बल के लिए अनुपात form रूप लेते हैं

, (4)

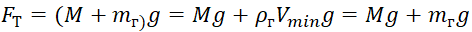
, (5)

जहाँ: एम समताप मंडल के गुब्बारे के खोल और उपकरणों का द्रव्यमान है;

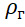
हीलियम का घनत्व है।

संबंधों की समानता (4) और (5), यह मानते हुए कि शेल V का आयतन LALV की ऊंचाई का एक कार्य है, हम अनुपात प्राप्त करते हैं:

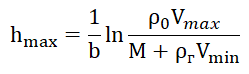
। (6)

संबंध में शामिल मापदंडों के संख्यात्मक मान (6) एक ग्राफ के निर्माण के लिए लिस्टिंग में दिए गए हैं, जो केवल संकेतित उद्देश्य के लिए दिया गया है।

डेटा के साथ एक चार्ट सूचीबद्ध करना

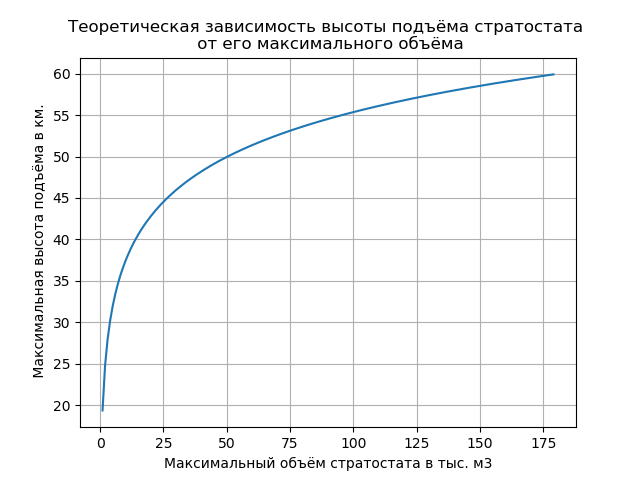
 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. Vmin=400#    /3. b=0.000128# ,      1/. c=0.8#   mo=40#   rs=rg+mo/Vmin#    ,     p1=rv/rs#   h=[(10**-3)*log((rv*w)/(mo+rg*Vmin))*b**-1 for w in arange(1*10**3,1.8*10**5,1000)] v=[(10**-3)*w for w in arange(1*10**3,1.8*10**5,1000)] plt.title("     \n    ") plt.plot(v,h) plt.xlabel('    . 3') plt.ylabel('     .') plt.grid(True) plt.show()

हमें मिलता है:

कार्यक्रम लिस्टिंग में सूचीबद्ध LALV मापदंडों को बदलकर, आप दिए गए ग्राफ़ को प्राप्त कर सकते हैं और डिज़ाइन के दौरान आवश्यक अधिकतम शेल मात्रा का चयन कर सकते हैं। ऐसे उपकरणों के निर्माण में विशाल अनुभव का उपयोग करके परिणामों का शोधन किया जाता है।

निष्कर्ष:

हवा से हल्के दो प्रकार के विमान के गणितीय मॉडल प्राप्त किए जाते हैं, जो वायु पर्यावरण की आदर्श परिस्थितियों में ऐसे उपकरणों के मापदंडों का मूल्यांकन करने के लिए कम्प्यूटेशनल प्रयोगों की अनुमति देते हैं।
विभेदक समीकरणों की प्रणाली के संख्यात्मक समाधान के लिए प्रस्तावित बहु-चरण योजना किसी को होवरिंग और डिसेंट के उदय के चरणों में हवा की तुलना में हल्का विमान के ऊर्ध्वाधर प्रक्षेपवक्र प्राप्त करने की अनुमति देती है।

संदर्भ

एयरशिप के बारे में कुछ शब्द
अंतरिक्ष के रास्ते पर। समताप-मंडल का बैलून
रियाज़िकोव यू.आई. आधुनिक फोरट्रान। - सेंट पीटर्सबर्ग: क्राउन प्रिंट, 2004 ।-- 288 पी।

एक विमान की ऊर्ध्वाधर उड़ान की गतिशीलता हवा की तुलना में हल्की होती है

परिचय

एक गेंद के आकार में एक खोल के साथ LALV की उड़ान का एक गणितीय मॉडल, जिसकी मात्रा ऊंचाई के साथ नहीं बदलती है

LALV हवा के तापमान के बढ़ने की गति और ऊंचाई पर प्रभाव

शुरू से लैंडिंग तक एसएएलवी उड़ान के सभी चरणों की विशेषताओं का निर्धारण

शेल के साथ एलएएलवी की उड़ान का एक गणितीय मॉडल, जिसकी मात्रा ऊंचाई के साथ बदलती है

संदर्भ

More articles: