 तार का सिद्धांत इस विचार पर आधारित है कि शून्य-आयामी प्राथमिक कणों के बजाय, ब्रह्मांड में एक-आयामी तार होते हैं
तार का सिद्धांत इस विचार पर आधारित है कि शून्य-आयामी प्राथमिक कणों के बजाय, ब्रह्मांड में एक-आयामी तार होते हैंस्ट्रिंग सिद्धांत भौतिकी के सबसे शानदार, विरोधाभासी और अप्रमाणित विचारों में से एक है। यह एक भौतिक प्रवृत्ति पर आधारित है जो कई शताब्दियों तक जीवित रहा है - कि कुछ मौलिक स्तर पर, वास्तविकता के सभी विभिन्न बलों, कणों, इंटरैक्शन और अभिव्यक्तियों को एक मंच के विभिन्न भागों के रूप में एक साथ जोड़ा जाता है। चार स्वतंत्र मूलभूत इंटरैक्शन के बजाय - मजबूत, विद्युत चुम्बकीय, कमजोर और गुरुत्वाकर्षण - एक एकीकृत सिद्धांत है जो उन सभी को गले लगाता है।
कई मायनों में, स्ट्रिंग सिद्धांत गुरुत्वाकर्षण के क्वांटम सिद्धांत के लिए सबसे अच्छा उम्मीदवार है, जो उच्चतम ऊर्जा स्तरों पर बातचीत का संयोजन करता है। हालांकि इसके लिए कोई प्रायोगिक साक्ष्य नहीं है, लेकिन यह मानने के लिए सैद्धांतिक कारण मजबूर हैं कि ऐसा है। 2015 में, सबसे बड़े जीवित स्ट्रिंग सिद्धांत विशेषज्ञ, एडवर्ड विटेन ने एक
पेपर लिखा था, जिसे प्रत्येक भौतिक विज्ञानी को स्ट्रिंग सिद्धांत के बारे में जानना चाहिए। और यहाँ इसका मतलब है - भले ही आप भौतिक विज्ञानी न हों।
 बिंदु कणों के लिए क्वांटम क्षेत्र सिद्धांत (बाएं) के मानक इंटरैक्शन और बंद तारों के लिए स्ट्रिंग सिद्धांत (दाएं) में बातचीत के बीच अंतर।
बिंदु कणों के लिए क्वांटम क्षेत्र सिद्धांत (बाएं) के मानक इंटरैक्शन और बंद तारों के लिए स्ट्रिंग सिद्धांत (दाएं) में बातचीत के बीच अंतर।यह आश्चर्यजनक है कि कभी-कभी प्रकृति के नियमों में बहुत सी समानताएं पाई जाती हैं, जो प्रतीत होता है कि असंबंधित घटना से संबंधित हैं। ऐसी घटनाओं की गणितीय संरचना अक्सर बहुत समान होती है, और कभी-कभी समान भी होती है। न्यूटन के नियमों के अनुसार दो विशाल निकायों का आकर्षण विद्युत आवेशित कणों के आकर्षण / प्रतिकर्षण के लगभग समान है। पेंडुलम के दोलन एक तारे के चारों ओर एक वसंत या ग्रह पर द्रव्यमान के आंदोलन के लिए पूरी तरह से अनुरूप हैं। गुरुत्वाकर्षण तरंगें, जल तरंगें, प्रकाश तरंगें - इन सभी में आश्चर्यजनक रूप से समान गुण होते हैं, इस तथ्य के बावजूद कि यह मौलिक रूप से भौतिक स्रोतों से आता है। और एक ही नस में, हालांकि कई को इसका एहसास नहीं है, एक कण का क्वांटम सिद्धांत और गुरुत्वाकर्षण के क्वांटम सिद्धांत के दृष्टिकोण भी एक दूसरे के समान हैं।
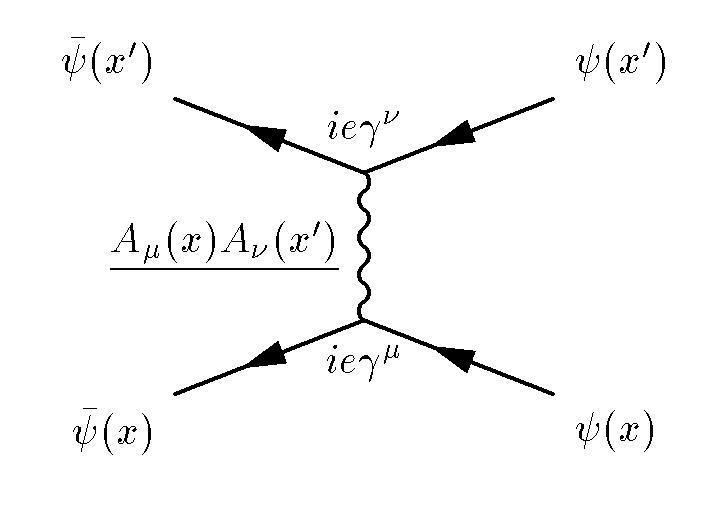 फेनमैन आरेख दो इलेक्ट्रॉनों के बिखरने का प्रतिनिधित्व करता है - इसके लिए कण इंटरैक्शन के सभी संभावित इतिहासों को संक्षेप में प्रस्तुत करना आवश्यक है
फेनमैन आरेख दो इलेक्ट्रॉनों के बिखरने का प्रतिनिधित्व करता है - इसके लिए कण इंटरैक्शन के सभी संभावित इतिहासों को संक्षेप में प्रस्तुत करना आवश्यक हैक्वांटम क्षेत्र सिद्धांत इस तरह से काम करता है: एक कण ले लो और गणितीय "इसकी सभी कहानियों का योग" करें। आप केवल यह गणना नहीं कर सकते हैं कि कण कहां था, और यह अब कहां है, और यह वहां कैसे मिला - क्योंकि प्रकृति में एक आंतरिक और मौलिक क्वांटम अनिश्चितता है। इसके बजाय, हम सभी संभावित तरीकों को संक्षेप में प्रस्तुत करते हैं जिसमें यह वर्तमान स्थिति ("पिछले इतिहास") में आ सकता है, इसी संभाव्य भार के साथ, और फिर एक कण की क्वांटम स्थिति की गणना कर सकते हैं।
गुरुत्वाकर्षण के साथ काम करने के लिए, और क्वांटम कणों के साथ नहीं, आपको थोड़ा बदलने की जरूरत है। चूंकि आइंस्टीन के जनरल थ्योरी ऑफ रिलेटिविटी कणों से नहीं, बल्कि स्पेस-टाइम की वक्रता के साथ जुड़े हुए हैं, इसलिए हम सभी संभव कण इतिहास औसत नहीं करेंगे। इसके बजाय, हम सभी संभावित स्पेस-टाइम जियोमेट्रीज को एवरेज करते हैं।
 क्वांटम भौतिकी के नियमों के अनुसार आइंस्टीन और बाकी सब कुछ (मजबूत, कमजोर और विद्युत चुम्बकीय बातचीत) के नियमों के अनुसार गुरुत्वाकर्षण ब्रह्मांड में सब कुछ नियंत्रित करने वाले कानूनों के दो अलग-अलग सेट हैं।
क्वांटम भौतिकी के नियमों के अनुसार आइंस्टीन और बाकी सब कुछ (मजबूत, कमजोर और विद्युत चुम्बकीय बातचीत) के नियमों के अनुसार गुरुत्वाकर्षण ब्रह्मांड में सब कुछ नियंत्रित करने वाले कानूनों के दो अलग-अलग सेट हैं।तीन स्थानिक आयामों में काम करना बहुत मुश्किल है, और जब हम एक जटिल शारीरिक समस्या का सामना करते हैं, तो हम अक्सर पहले इसका एक सरल संस्करण हल करने की कोशिश करते हैं। यदि आप एक आयाम से नीचे जाते हैं, तो सब कुछ आसान हो जाएगा। एकमात्र संभव एक आयामी सतह एक खुली स्ट्रिंग है, जिसमें दो अलग-अलग छोर होते हैं जो एक दूसरे से जुड़े नहीं होते हैं, या एक बंद स्ट्रिंग, जिनमें से छोर जुड़े हुए हैं और एक लूप बनाते हैं। इसके अलावा, अंतरिक्ष की वक्रता - तीन आयामों में बहुत जटिल - एक तुच्छ मामला बन जाता है। इसलिए, यदि हम मामले को जोड़ना चाहते हैं, तो हम स्केलर फ़ील्ड्स का उपयोग करते हैं (जैसे एक निश्चित प्रकार के कणों के लिए) और एक कॉस्मोलॉजिकल स्थिरांक (द्रव्यमान के लिए जिम्मेदार समीकरण के सदस्य के रूप में काम करना): एक महान सादृश्य।
स्वतंत्रता का अतिरिक्त अंश जो एक कण को कई आयामों में प्राप्त होता है, एक विशेष भूमिका नहीं निभाता है; जब तक हम संवेग वेक्टर को निर्धारित कर सकते हैं, यह मुख्य आयाम रहता है। इसलिए, एक आयाम में, क्वांटम गुरुत्वाकर्षण किसी भी तरह के आयामों में एक मुक्त क्वांटम कण की तरह दिखता है।
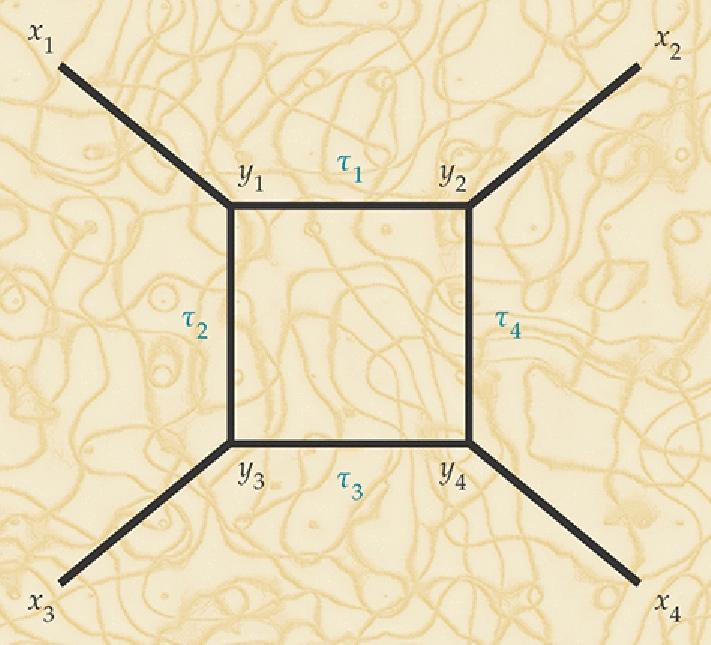 कोने के साथ एक ग्राफ जहां तीन किनारों को मिलाते हैं, एक आयामी क्वांटम गुरुत्वाकर्षण से संबंधित पथ के निर्माण का एक प्रमुख घटक है
कोने के साथ एक ग्राफ जहां तीन किनारों को मिलाते हैं, एक आयामी क्वांटम गुरुत्वाकर्षण से संबंधित पथ के निर्माण का एक प्रमुख घटक हैअगला कदम इंटरैक्शन को चालू करना है, और एक मुक्त कण से
तितर-बितर किए बिना
एम्पलीट्यूड या
प्रभावी क्रॉस सेक्शन को स्थानांतरित करना है जिसमें ब्रह्मांड से जुड़ी एक भौतिक भूमिका हो सकती है। ऊपर दिए गए ग्राफ़ के समान ही हमें क्वांटम गुरुत्व में क्रिया की भौतिक अवधारणा का वर्णन करने की अनुमति देते हैं। यदि हम ऐसे ग्राफ़ के सभी संभावित संयोजनों को लिखते हैं और उन्हें सारांशित करते हैं - सामान्य रूप से समान कानूनों का उपयोग करते हुए, उदाहरण के लिए, संवेग के संरक्षण का नियम - हम सादृश्य को पूरा कर सकते हैं। एक आयाम में क्वांटम गुरुत्वाकर्षण किसी भी संख्या के आयाम में एक कण की बातचीत के समान है।
 किसी विशेष स्थान पर एक क्वांटम कण का पता लगाने की संभावना कभी भी 100% नहीं होती है; संभावना अंतरिक्ष और समय पर वितरित की जाती है।
किसी विशेष स्थान पर एक क्वांटम कण का पता लगाने की संभावना कभी भी 100% नहीं होती है; संभावना अंतरिक्ष और समय पर वितरित की जाती है।अगला कदम एक स्थानिक आयाम से 3 + 1 आयामों की ओर बढ़ना है: जहां ब्रह्मांड के तीन स्थानिक और एक अस्थायी आयाम हैं। लेकिन गुरुत्वाकर्षण के लिए यह सैद्धांतिक "अपग्रेड" बहुत मुश्किल हो सकता है। यदि हम विपरीत दिशा में काम करने का निर्णय लेते हैं तो एक अलग दृष्टिकोण पाया जा सकता है।
किसी भी संख्या के आयाम में एक कण (शून्य-आयामी इकाई) के व्यवहार को गिनने के बजाय, शायद हम एक स्ट्रिंग, खुले या बंद (एक-आयामी इकाई) के व्यवहार को गिन सकते हैं। और इस आधार पर, पहले से ही अधिक यथार्थवादी संख्या के आयामों में क्वांटम गुरुत्व के अधिक पूर्ण सिद्धांत के लिए समानताएं देखें।
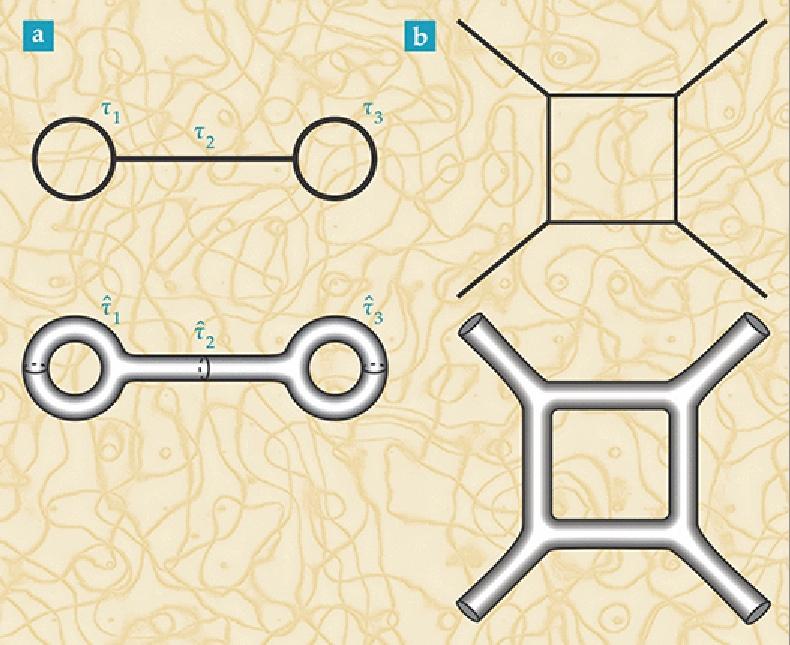 फेनमैन आरेख (ऊपर) बिंदु कणों और उनकी बातचीत पर आधारित हैं। स्ट्रिंग सिद्धांत (नीचे) के लिए उन्हें एनालॉग में बदलकर, हमें ऐसी सतहें मिलती हैं जिनमें गैर-तुच्छ वक्रता हो सकती है।
फेनमैन आरेख (ऊपर) बिंदु कणों और उनकी बातचीत पर आधारित हैं। स्ट्रिंग सिद्धांत (नीचे) के लिए उन्हें एनालॉग में बदलकर, हमें ऐसी सतहें मिलती हैं जिनमें गैर-तुच्छ वक्रता हो सकती है।अंक और इंटरैक्शन के बजाय, हम तुरंत सतहों, झिल्लियों और इतने पर काम करना शुरू कर देते हैं। एक सच्ची बहुआयामी सतह प्राप्त करने के बाद, हम इसे गैर-तुच्छ तरीकों से मोड़ सकते हैं। हम उसके बहुत दिलचस्प व्यवहार का निरीक्षण करना शुरू करते हैं; एक जो जीआर के ढांचे में ब्रह्मांड में देखे गए अंतरिक्ष-समय की वक्रता का आधार हो सकता है।
लेकिन यद्यपि एक आयामी क्वांटम गुरुत्वाकर्षण हमें कणों के लिए क्वांटम क्षेत्र सिद्धांत देता है, संभवतः घुमावदार अंतरिक्ष समय में, यह अकेले गुरुत्वाकर्षण का वर्णन नहीं करता है। इस पहेली में क्या गायब है? ऑपरेटरों, या क्वांटम-मैकेनिकल इंटरैक्शन और गुणों का प्रतिनिधित्व करने वाले कार्यों के बीच कोई पत्राचार नहीं है, साथ ही यह भी बताता है कि समय के साथ कण और उनके गुण कैसे बदलते हैं। "राज्य-संचालकों" का यह पत्राचार एक आवश्यक लेकिन लापता घटक था।
लेकिन अगर हम बिंदु कणों से स्ट्रिंग संस्थाओं में जाते हैं, तो यह पत्राचार प्रकट होता है।
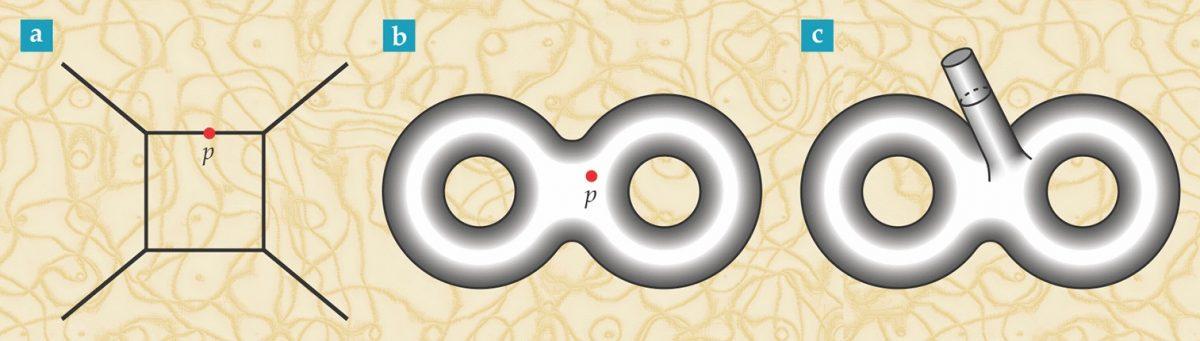 अंतरिक्ष-समय मीट्रिक की विकृति को एक उतार-चढ़ाव ('पी') द्वारा दर्शाया जा सकता है, और यदि स्ट्रिंग सादृश्य पर लागू किया जाता है, तो यह अंतरिक्ष-समय के उतार-चढ़ाव का वर्णन करेगा और स्ट्रिंग की क्वांटम स्थिति के अनुरूप होगा।
अंतरिक्ष-समय मीट्रिक की विकृति को एक उतार-चढ़ाव ('पी') द्वारा दर्शाया जा सकता है, और यदि स्ट्रिंग सादृश्य पर लागू किया जाता है, तो यह अंतरिक्ष-समय के उतार-चढ़ाव का वर्णन करेगा और स्ट्रिंग की क्वांटम स्थिति के अनुरूप होगा।कणों से तारों तक संक्रमण में, ऑपरेटर-राज्यों का एक वास्तविक पत्राचार दिखाई देता है। अंतरिक्ष-समय मीट्रिक (यानी, ऑपरेटर) में उतार-चढ़ाव स्ट्रिंग गुणों के क्वांटम-मैकेनिकल विवरण में स्वचालित रूप से राज्य का प्रतिनिधित्व करता है। इसलिए, अंतरिक्ष-समय में गुरुत्वाकर्षण के क्वांटम सिद्धांत को स्ट्रिंग सिद्धांत के आधार पर बनाया जा सकता है।
लेकिन यह सब हमें नहीं मिलता है: हम क्वांटम गुरुत्व भी प्राप्त करते हैं, जो अंतरिक्ष समय में अन्य कणों और इंटरैक्शन के साथ संयुक्त होते हैं, जो उन लोगों के साथ हैं जो फील्ड सिद्धांत में अन्य स्ट्रिंग ऑपरेटरों के अनुरूप हैं। एक ऑपरेटर भी है जो अंतरिक्ष-समय ज्यामिति में उतार-चढ़ाव का वर्णन करता है, और स्ट्रिंग के क्वांटम राज्यों के लिए एक और एक है। स्ट्रिंग सिद्धांत के बारे में सबसे दिलचस्प बात यह है कि यह हमें गुरुत्वाकर्षण के एक काम कर रहे क्वांटम सिद्धांत दे सकता है।
 ब्रायन ग्रीन स्ट्रिंग सिद्धांत पर एक प्रस्तुति देता है
ब्रायन ग्रीन स्ट्रिंग सिद्धांत पर एक प्रस्तुति देता हैइसका मतलब यह नहीं है कि इस मुद्दे को हल कर दिया गया है, और यह स्ट्रिंग सिद्धांत क्वांटम गुरुत्वाकर्षण का मार्ग है। स्ट्रिंग थ्योरी की बहुत उम्मीद है कि इन उपमाओं को सभी पैमानों पर बनाए रखा जा सकता है, और यह कि दुनिया और ब्रह्मांड की स्ट्रिंग तस्वीर का एक असमान रूप से एक-से-एक पत्राचार होगा जिसे हम अपने आसपास देखते हैं।
अब तक, तार और सुपरस्ट्रिंग्स के साथ दुनिया की तस्वीर केवल कुछ ही आयामों में सुसंगत है, और उनमें से सबसे आशाजनक हमें चार आयामी आइंस्टीन के गुरुत्वाकर्षण नहीं देता है, जो हमारे ब्रह्मांड का वर्णन करता है। इसके बजाय, हम
Brans - Dicke द्वारा गुरुत्वाकर्षण के 10-आयामी
सिद्धांत की खोज करते हैं। हमारे ब्रह्मांड में विद्यमान गुरुत्वाकर्षण को बहाल करने के लिए, छह आयामों से "छुटकारा" आवश्यक है और युग्मन स्थिरांक को अनंत तक निर्देशित करना आवश्यक है।
यदि आपने "कॉम्पैक्टीफिकेशन" शब्द को स्ट्रिंग सिद्धांत पर लागू किया है, तो यह केवल एक शब्द है जिसका अर्थ है कि हमें इन पहेलियों को हल करना चाहिए। अब तक, कई लोगों ने एक पूर्ण और ठोस समाधान का सुझाव दिया है जो कॉम्पैक्टिफ़िकेशन के लिए उपयुक्त है। लेकिन आइंस्टीन का गुरुत्वाकर्षण कैसे प्राप्त करें और 10-आयामी सिद्धांत से 3 + 1 आयाम का सवाल खुला रहता है।
 कैलाबी-याउ मैनिफोल्ड का द्वि-आयामी प्रक्षेपण, स्ट्रिंग सिद्धांत के अतिरिक्त, अनावश्यक मापों को संकुचित करने के लोकप्रिय तरीकों में से एक
कैलाबी-याउ मैनिफोल्ड का द्वि-आयामी प्रक्षेपण, स्ट्रिंग सिद्धांत के अतिरिक्त, अनावश्यक मापों को संकुचित करने के लोकप्रिय तरीकों में से एकस्ट्रिंग थ्योरी क्वांटम गुरुत्व को एक मार्ग प्रदान करता है जिसकी तुलना कुछ ही विकल्प कर सकते हैं। यदि हम इस बारे में उचित निष्कर्ष देते हैं कि गणित कैसे काम करता है, तो हम इसे सामान्य सापेक्षता और मानक मॉडल दोनों से प्राप्त कर सकते हैं। आज, यह एकमात्र विचार है जो हमें यह देता है - इसलिए यह बहुत सख्त पीछा है। इससे कोई फर्क नहीं पड़ता कि आप स्ट्रिंग थ्योरी की सफलता या विफलता के लिए खड़े हैं, या आप कैसे सत्यापित भविष्यवाणियों की कमी के बारे में महसूस करते हैं, यह, बिना किसी संदेह के, सैद्धांतिक भौतिकी में अनुसंधान के सबसे सक्रिय क्षेत्रों में से एक है। वास्तव में, स्ट्रिंग सिद्धांत भौतिकविदों के अंतिम सिद्धांत के सपनों के बीच अग्रणी विचार के रूप में खड़ा है।