प्रविष्टि सॉर्टिंग का सामान्य सार निम्नानुसार है:
- एरे के अनसरे हिस्से में तत्वों पर फेरबदल करता है।
- प्रत्येक तत्व को उस स्थान पर सरणी के सॉर्ट किए गए हिस्से में डाला जाता है जहां यह होना चाहिए।
यह, सिद्धांत रूप में, आपको आवेषण द्वारा छंटाई के बारे में जानने की आवश्यकता है। यही है, सम्मिलन प्रकार हमेशा सरणी को 2 भागों में विभाजित करता है - सॉर्ट किया गया और अनसुलझा। किसी भी आइटम को अनसोल्ड भाग से पुनर्प्राप्त किया जाता है। चूंकि सरणी के दूसरे भाग को क्रमबद्ध किया गया है, आप इस निकाले गए तत्व के लिए इस सरणी में जल्दी से अपना स्थान पा सकते हैं। तत्व को जहां आवश्यक हो डाला जाता है, जिसके परिणामस्वरूप सरणी का छांटा हुआ हिस्सा बढ़ता है, और अनसुलझा हिस्सा कम हो जाता है। वह सब है। इस सिद्धांत द्वारा सभी प्रकार के आवेषण काम करते हैं।
इस दृष्टिकोण में सबसे कमजोर बिंदु एक तत्व को सरणी के सॉर्ट किए गए भाग में सम्मिलित कर रहा है। वास्तव में, यह आसान नहीं है और इस कदम को पूरा करने के लिए आपको किन चालों पर चलना होगा।
सरल सम्मिलन छँटाई

हम बाएं से दाएं सरणी के माध्यम से जाते हैं और प्रत्येक तत्व को बदले में संसाधित करते हैं। अगले तत्व के बाईं ओर, हम सरणी के सॉर्ट किए गए हिस्से को दाईं ओर बढ़ाते हैं, जैसे-जैसे प्रक्रिया आगे बढ़ती है, वैसे-वैसे अनसुलझा हिस्सा धीरे-धीरे वाष्पित हो जाता है। सरणी के सॉर्ट किए गए भाग में, अगले तत्व के लिए सम्मिलन बिंदु खोजा जाता है। तत्व को स्वयं बफर में भेजा जाता है, जिसके परिणामस्वरूप सरणी में एक खाली सेल दिखाई देती है - यह आपको तत्वों को स्थानांतरित करने और सम्मिलन बिंदु को मुक्त करने की अनुमति देता है।
def insertion(data): for i in range(len(data)): j = i - 1 key = data[i] while data[j] > key and j >= 0: data[j + 1] = data[j] j -= 1 data[j + 1] = key return data
उदाहरण के रूप में सरल आवेषण का उपयोग करना, आवेषण का मुख्य लाभ (लेकिन सभी नहीं!) आवेषण द्वारा छंटनी प्रदर्शनात्मक रूप से दिखाई देती है, अर्थात्, लगभग ऑर्डर किए गए सरणियों का बहुत तेज़ प्रसंस्करण:

इस परिदृश्य में, यहां तक कि छँटाई आवेषण के सबसे आदिम कार्यान्वयन बड़े सरणियों सहित कुछ छँटाई तेजी के लिए सुपर-अनुकूलित एल्गोरिथ्म से आगे निकलने की संभावना है।
यह इस वर्ग के मुख्य विचार से सुगम है - सरणी के अनसुने हिस्से से तत्वों को स्थानांतरित करके सॉर्ट किया गया। समान परिमाण के डेटा की निकटता के साथ, सम्मिलन बिंदु आमतौर पर सॉर्ट किए गए भाग के किनारे के करीब स्थित होता है, जो आपको कम से कम ओवरहेड के साथ सम्मिलित करने की अनुमति देता है।
प्रविष्टि सॉर्टिंग की तुलना में लगभग ऑर्डर किए गए सरणियों को संभालने के लिए कुछ भी बेहतर नहीं है। जब आप कहीं जानकारी प्राप्त करते हैं कि आवेषण द्वारा छँटाई का सबसे अच्छा समय जटिलता
ओ ( n ) है , तो सबसे अधिक संभावना है कि आप लगभग ऑर्डर किए गए सरणियों के साथ स्थितियों का उल्लेख कर रहे हैं।
सरल बाइनरी खोज आवेषण द्वारा क्रमबद्ध करें

चूंकि डालने का स्थान सरणी के सॉर्ट किए गए हिस्से में खोजा जाता है, इसलिए द्विआधारी खोज का उपयोग करने का विचार खुद को बताता है। एक और बात यह है कि एल्गोरिथ्म के समय की जटिलता के लिए सम्मिलन साइट की खोज महत्वपूर्ण नहीं है (मुख्य संसाधन भक्षक तत्व को मिली स्थिति में डालने का चरण है), इसलिए यह अनुकूलन बहुत कम करता है।
और लगभग छाँटे गए सरणी के मामले में, एक द्विआधारी खोज धीमी गति से भी काम कर सकती है, क्योंकि यह सॉर्ट किए गए अनुभाग के बीच से शुरू होती है, जो कि, सबसे अधिक संभावना है, सम्मिलन बिंदु से बहुत दूर होगी (और तत्व स्थिति से सम्मिलन बिंदु तक एक सामान्य खोज करने के लिए कम कदम उठाएगी यदि डेटा एक पूरे के रूप में सरणी में)।
def insertion_binary(data): for i in range(len(data)): key = data[i] lo, hi = 0, i - 1 while lo < hi: mid = lo + (hi - lo) // 2 if key < data[mid]: hi = mid else: lo = mid + 1 for j in range(i, lo + 1, -1): data[j] = data[j - 1] data[lo] = key return data
बाइनरी खोज की रक्षा में, मैं ध्यान देता हूं कि वह आवेषण द्वारा अन्य सॉर्टिंग की प्रभावशीलता में अंतिम शब्द कह सकता है। उसके लिए धन्यवाद, विशेष रूप से, एल्गोरिदम जैसे लाइब्रेरियन सॉर्टिंग और सॉलिटेयर सॉर्टिंग औसत समय जटिलता
ओ ( एन लॉग एन ) पर जाते हैं । लेकिन उनके बारे में बाद में।
सरल आवेषण द्वारा जोड़ी छँटाई
साधारण आवेषण का संशोधन, ओरेकल कॉर्पोरेशन की गुप्त प्रयोगशालाओं में विकसित किया गया है। यह सॉर्टिंग JDK का हिस्सा है, और ड्यूल-पिवट क्विकॉर्ट का हिस्सा है। इसका उपयोग छोटे सरणियों (47 तत्वों तक) को छांटने और बड़े सरणियों के छोटे क्षेत्रों को सॉर्ट करने के लिए किया जाता है।

एक नहीं बल्कि दो आसन्न तत्वों को एक बार बफर में भेजा जाता है। सबसे पहले, जोड़ी का बड़ा तत्व डाला जाता है, और इसके तुरंत बाद, सरल सम्मिलन विधि जोड़ी के छोटे तत्व पर लागू होती है।
यह क्या देता है? एक जोड़ी से एक छोटी सी वस्तु को संभालने के लिए बचत। उसके लिए, सम्मिलन बिंदु और सम्मिलन के लिए खोज केवल सरणी के उस सॉर्ट किए गए भाग पर की जाती है, जिसमें जोड़े से बड़े तत्व को संसाधित करने के लिए उपयोग किए गए सॉर्ट किए गए क्षेत्र शामिल नहीं होते हैं। यह संभव हो जाता है क्योंकि बाहरी लूप के एक पास में बड़े और छोटे तत्वों को तुरंत एक के बाद एक संसाधित किया जाता है।
यह औसत समय की जटिलता को प्रभावित नहीं करता है (यह अभी भी
ओ ( एन 2 ) के बराबर है
), हालांकि, युग्मित आवेषण सामान्य लोगों की तुलना में थोड़ी तेजी से काम करते हैं।
मैं पायथन में एल्गोरिदम का वर्णन करता हूं, लेकिन यहां मैं जावा में मूल स्रोत (पठनीयता के लिए संशोधित) देता हूं:
for (int k = left; ++left <= right; k = ++left) {
शेल सॉर्ट

यह एल्गोरिथ्म यह निर्धारित करने में एक बहुत ही मजाकिया दृष्टिकोण है कि सरणी के किस हिस्से को सॉर्ट किया गया है। सरल आवेषण में, सब कुछ सरल है: वर्तमान तत्व से, बाईं ओर सब कुछ पहले से ही सॉर्ट किया गया है, दाईं ओर सब कुछ अभी तक सॉर्ट नहीं किया गया है। सरल आवेषण के विपरीत, शैल छांटना तुरंत तत्व के बाईं ओर सरणी का एक कड़ाई से क्रमबद्ध भाग बनाने की कोशिश नहीं करता है। यह एरे के
लगभग छँटे हुए हिस्से को तत्व के बाईं ओर बनाता है और इसे जल्दी से पर्याप्त करता है।
शेल छँटाई वर्तमान तत्व को बफर में फेंक देता है और इसे सरणी के बाईं ओर से तुलना करता है। यदि यह बाईं ओर बड़े तत्व पाता है, तो यह उन्हें दाईं ओर शिफ्ट करता है, जिससे सम्मिलन के लिए जगह बनती है। लेकिन एक ही समय में यह पूरे बाएं हिस्से को नहीं लेता है, लेकिन इसमें से तत्वों का केवल एक निश्चित समूह होता है, जहां तत्वों को एक निश्चित दूरी से एक दूसरे से अलग रखा जाता है। ऐसी प्रणाली आपको तत्वों को जल्दी से सरणी के लगभग उस क्षेत्र में सम्मिलित करने की अनुमति देती है जहां उन्हें स्थित होना चाहिए।
मुख्य लूप के प्रत्येक पुनरावृत्ति के साथ, यह दूरी धीरे-धीरे कम हो जाती है और जब यह एक के बराबर हो जाती है, तो इस समय शैल छांटना साधारण आवेषण के साथ एक क्लासिक प्रकार में बदल जाता है, जिसे लगभग सॉर्ट किए गए सरणी के प्रसंस्करण के लिए दिया गया था। एक लगभग सॉर्ट किया गया सरणी पूरी तरह से सॉर्ट किए गए आवेषण को जल्दी से परिवर्तित करता है।
def shell(data): inc = len(data) // 2 while inc: for i, el in enumerate(data): while i >= inc and data[i - inc] > el: data[i] = data[i - inc] i -= inc data[i] = el inc = 1 if inc == 2 else int(inc * 5.0 / 11) return data
एक समान सिद्धांत द्वारा संयुक्त छंटाई बुलबुला छंटाई में सुधार करती है, इसलिए
ओ ( एन 2 ) के साथ एल्गोरिथ्म की समय जटिलता
ओ ( एन लॉग एन ) तक सही कूदती है। काश, शेल इस उपलब्धि को दोहराने का प्रबंधन नहीं करता - सबसे अच्छा समय जटिलता
ओ ( एन लॉग 2 एन ) तक पहुंचता है।
शेल को छांटने के बारे में कई हैबराती लिखा गया है, इसलिए हमें जानकारी के साथ अतिभारित नहीं किया जाएगा और आगे बढ़ना होगा।
पेड़ की छँटाई
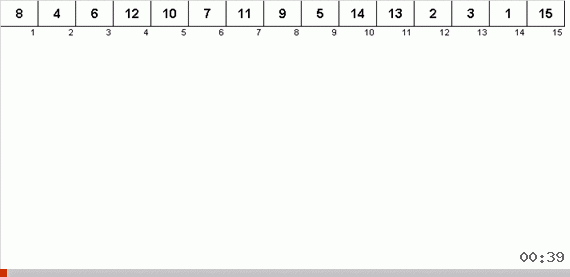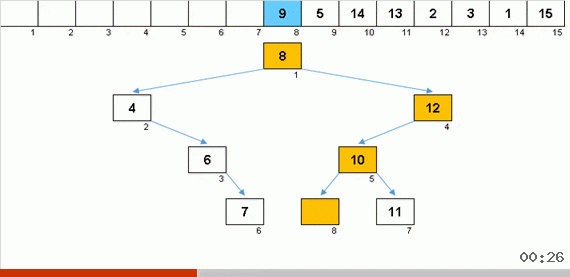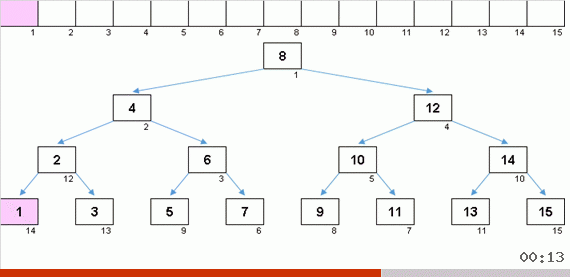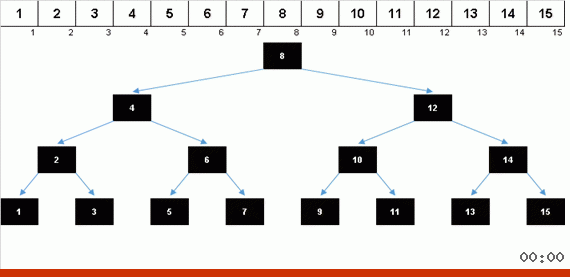
अतिरिक्त मेमोरी के कारण एक पेड़ के साथ छंटनी करने से सरणी के सॉर्ट किए गए हिस्से में एक और तत्व जोड़ने की समस्या जल्दी से हल हो जाती है। इसके अलावा, बाइनरी ट्री सरणी के सॉर्ट किए गए भाग के रूप में कार्य करता है। तत्वों पर पुनरावृत्ति होने पर एक पेड़ सचमुच मक्खी पर बनता है।
तत्व की तुलना पहले रूट के साथ की जाती है, और फिर सिद्धांत के अनुसार अधिक नेस्टेड नोड्स के साथ: यदि तत्व नोड से छोटा है, तो हम बाईं शाखा से नीचे जाते हैं, यदि कम नहीं है, तो दाईं ओर। इस तरह के नियम से निर्मित वृक्ष को आसानी से दरकिनार किया जा सकता है ताकि निचले मानों के साथ नोड्स से बड़े मानों के साथ नोड्स में स्थानांतरित हो सकें (और इस प्रकार बढ़ते हुए सभी तत्व प्राप्त करें)
आवेषण द्वारा सॉर्टिंग का मुख्य स्नैग (सरणी के सॉर्ट किए गए हिस्से में एक तत्व को अपनी जगह पर डालने की लागत) को हल किया जाता है, निर्माण काफी तेज़ी से आगे बढ़ता है। किसी भी मामले में, सम्मिलन बिंदु को मुक्त करने के लिए, तत्वों के कारवां को धीरे-धीरे स्थानांतरित करने के लिए आवश्यक नहीं है जैसा कि पिछले एल्गोरिदम में है। ऐसा लगता है कि यहाँ यह है, छँटाई आवेषण का सबसे अच्छा। लेकिन एक समस्या है।
जब आपको एक सुंदर सममित क्रिसमस ट्री (तथाकथित पूरी तरह से संतुलित पेड़) मिलता है, जैसा कि ऊपर दिए गए तीन पैराग्राफ में है, तो इंसर्ट जल्दी से होता है, क्योंकि इस मामले में पेड़ में सबसे कम संभव घोंसले का स्तर होता है। लेकिन एक यादृच्छिक सरणी से एक संतुलित (या कम से कम उस के करीब) संरचना शायद ही कभी प्राप्त की जाती है। और पेड़, सबसे अधिक संभावना है, अपूर्ण और असंतुलित होगा - विकृतियों के साथ, एक कूड़ेदार क्षितिज और अत्यधिक संख्या में स्तर।
इस क्रम में 1 से 10. मान वाले यादृच्छिक सरणी एक असंतुलित द्विआधारी वृक्ष उत्पन्न करते हैं: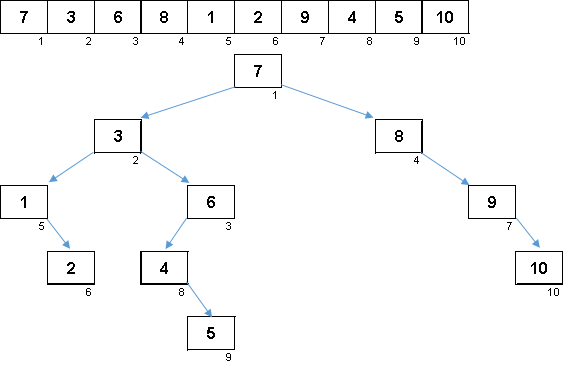
एक पेड़ बनाने के लिए पर्याप्त नहीं है, इसे अभी भी दरकिनार करने की आवश्यकता है। अधिक असंतुलन - मजबूत पेड़ के आघात एल्गोरिथ्म फिसल जाएगा। यहां, जैसा कि सितारों का कहना है, एक यादृच्छिक सरणी दोनों एक बदसूरत रोड़ा (जो अधिक होने की संभावना है) और पेड़ के समान भग्न पैदा कर सकता है।
तत्वों के मूल्य समान हैं, लेकिन क्रम अलग है। एक संतुलित बाइनरी ट्री उत्पन्न होता है: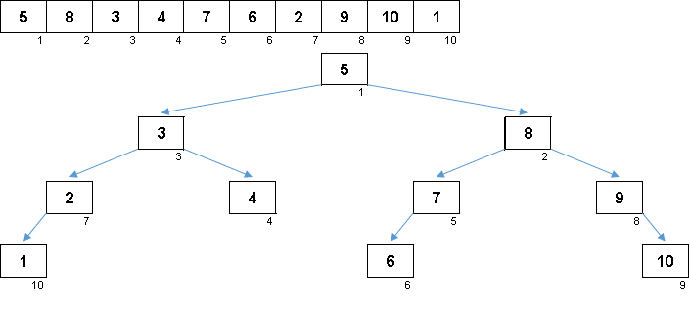
 सुंदर सकुरा पर
सुंदर सकुरा पर
पर्याप्त पंखुड़ी नहीं:
दर्जनों का एक द्विआधारी वृक्ष।असंतुलित पेड़ों की समस्या को उलटा छँटाई द्वारा हल किया जाता है, जो एक विशेष प्रकार के बाइनरी सर्च ट्री - स्प्ले ट्री का उपयोग करता है। यह एक अद्भुत ट्रांसफार्मर का पेड़ है, जिसे प्रत्येक ऑपरेशन के बाद संतुलित अवस्था में फिर से बनाया जाता है। इसके बारे में एक अलग लेख होगा। उस समय तक मैं ट्री सॉर्ट और सिपल सॉर्ट दोनों के लिए पायथन कार्यान्वयन तैयार कर दूंगा।
खैर, ठीक है, हम संक्षेप में सबसे लोकप्रिय छँटाई आवेषण के माध्यम से गए। सरल आवेषण, शेल और बाइनरी ट्री हम सभी स्कूल से जानते हैं। अब इस वर्ग के अन्य प्रतिनिधियों पर विचार करें, इतना व्यापक रूप से ज्ञात नहीं है।
विकी / विकी -
सम्मिलन , शेल / शेल , ट्री / ट्रीश्रृंखला लेख:
कौन AlgoLab का उपयोग करता है - मैं फ़ाइल को अपडेट करने की सलाह देता हूं। मैंने इस एप्लिकेशन में सरल द्विआधारी खोज आवेषण और युग्मित आवेषण जोड़े। उन्होंने शेल के लिए विज़ुअलाइज़ेशन को पूरी तरह से फिर से लिखा था (पिछले संस्करण में कुछ समझने के लिए नहीं था) और बाइनरी ट्री में एक तत्व सम्मिलित करते समय मूल शाखा में हाइलाइटिंग जोड़ा गया।