सस्टेनेबिलिटी जीएएन ट्रेनिंग

GAN विचार को पहली बार Jan Goodfellow Generative Adversarial Nets, Goodfellow et al 2014 द्वारा प्रकाशित किया गया था, जिसके बाद GAN सर्वश्रेष्ठ जेनेरेटिव मॉडल में से एक हैं।

किसी भी अन्य जेनिटल मॉडल की तरह, GAN कार्य डेटा मॉडल का निर्माण करना है, और अधिक विशेष रूप से, यह सीखें कि वितरण से नमूने कैसे उत्पन्न करें जितना संभव हो उतना डेटा वितरण के लिए (आमतौर पर एक सीमित आकार का डेटासेट है जिसमें हम डेटा वितरण को मॉडल करना चाहते हैं)।

GAN के फायदे बहुत बड़ी संख्या में हैं, लेकिन उनके पास एक महत्वपूर्ण दोष है - उन्हें प्रशिक्षित करना बहुत मुश्किल है।

हाल ही में, GAN स्थिरता पर कई कार्य जारी किए गए हैं:

• स्नातक वंशानुगत GAN अनुकूलन स्थानीय रूप से स्थिर है, वैष्णव नागराजन, जे। ज़िको कोल्टर, 2017
• द न्यूमेरिक्स ऑफ गन्स, लार्स मेसचेदर एट अल, 2017

उनके विचारों से प्रेरित होकर मैंने थोड़ा शोध किया।

मैंने पाठ को यथासंभव सरल बनाने की कोशिश की और, यदि संभव हो तो, केवल सबसे सरल गणित का उपयोग करें। दुर्भाग्य से, यह उचित ठहराने के लिए कि हम 2-आयामी वेक्टर फ़ील्ड के गुणों पर विचार क्यों कर सकते हैं, हमें विविधताओं की गणना की दिशा में थोड़ा खोदना होगा। लेकिन अगर कोई इन शर्तों से परिचित नहीं है, तो आप विभिन्न प्रकार के गण के लिए 2-आयामी वेक्टर फ़ील्ड के विचार पर तुरंत आगे बढ़ सकते हैं।

अब हम प्रशिक्षण प्रक्रिया के हुड को देखने और समझने की कोशिश करेंगे कि वहां क्या हो रहा है।

GAN, मुख्य समस्या

GANs में दो तंत्रिका नेटवर्क होते हैं: एक विभेदक और एक जनरेटर। जनरेटर - आपको कुछ वितरण से नमूना लेने की अनुमति देता है (आमतौर पर जनरेटर का वितरण कहा जाता है)। विवेचक मूल डेटासेट और जनरेटर से इनपुट नमूने प्राप्त करता है और भविष्यवाणी करना सीखता है कि यह नमूना (डेटासेट या जनरेटर) कहां से आता है।

GAN योजना:



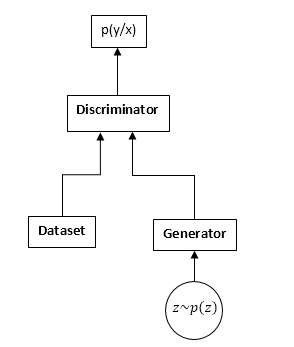
GAN प्रशिक्षण प्रक्रिया इस प्रकार है:

1. हम डेटासेट से n नमूने लेते हैं और जनरेटर से m नमूने लेते हैं।
2. हम जनरेटर वेट को ठीक करते हैं और डिस्क्रिमिनेटर मापदंडों को अपडेट करते हैं। यह एक सामान्य वर्गीकरण कार्य है। हमें सिर्फ अभिसरण तक विवेचक को प्रशिक्षित करने की आवश्यकता नहीं है। और तो और अक्सर यह दखल भी देता है।
3. हम डिस्क्रिमिनेटर वेट्स को ठीक करते हैं और जनरेटर वेट को अपडेट करते हैं, ताकि डिस्क्रिमिनेटर को यह सोचना शुरू हो जाए कि हमारे नमूने डेटासेट से हैं और जनरेटर से नहीं।
4. हम 1-3 को दोहराते हैं, जब तक कि भेदभावकर्ता और जनरेटर संतुलन में नहीं आते हैं (अर्थात, अन्य में से कोई भी अन्य को "धोखा" नहीं दे सकता है)।

हम विस्तार से GAN सीखने की प्रक्रिया की जांच नहीं करेंगे। इंटरनेट पर, और विशेष रूप से हब पर, इस प्रक्रिया को विस्तार से समझाने वाले कई लेख हैं।

हम कुछ पूरी तरह से अलग में दिलचस्पी लेंगे। अर्थात्, इस तथ्य के कारण कि हम दो तंत्रिका नेटवर्क के साथ प्रतिस्पर्धा कर रहे हैं, कार्य एक न्यूनतम (अधिकतम) के लिए खोज करना बंद कर देता है, लेकिन विशेष रूप से मामलों में एक काठी बिंदु की खोज में बदल जाता है (यानी, चरण 2 और 3 पर हम एक ही कार्यात्मक की कोशिश करते हैं विभेदक मापदंडों द्वारा अधिकतम और जनरेटर मापदंडों द्वारा कम से कम), और अधिक सामान्य चरण 2 और 3 में हम पूरी तरह से अलग कार्यात्मक का अनुकूलन कर सकते हैं। जाहिर है, न्यूनतम समस्या विभिन्न क्रियाकलापों के अनुकूलन का एक विशेष मामला है - एक कार्यात्मक को विभिन्न संकेतों के साथ लिया जाता है।

आइए इसे सूत्रों में देखें। हम मानते हैं कि pd (x) वह वितरण है जहां से डेटासेट को सैंपल किया जाता है, pg (x) जनरेटर का वितरण है, D (x) डिस्क्रिमिनेटर से आउटपुट है।

एक विवेचक को प्रशिक्षित करते समय, हम अक्सर ऐसी कार्यक्षमता को अधिकतम करते हैं:

$$

$$J \ = \ \ int {p_d (x) लॉग (D (x)) dx \ + \ \ int {p_g (x) लॉग (1 \ - \ D (x)) dx}}$$

वेक्टर वेक्टर:

$$

$$v = \ _ nabla_ \ theta J \ = \ int {\ frac {p_d (x)} {D (x)} \ nabla_ \ the थी D (x) \ dx \ + \ \ int \ {frac {p_g (x) )} {१ \ - \ D (x)} \ nabla_ \ the थी D (x) dx}}$$

जनरेटर का प्रशिक्षण देते समय, हम अधिकतम करते हैं:

$$

$$I \ = \ - \ int {p_g (x) लॉग (1 \ - \ D (x)) dx$$

इस मामले में ढाल के वेक्टर:

$$

$$u \ _ \ _ nabla_ \ varphi I \ = \ - \ int {{\ nabla_ \ varphi p} _g (x) लॉग (1 \ - \ D (x)) dx}$$

भविष्य में, हम देखेंगे कि क्रियाओं को क्रमशः बदला जा सकता है:

$$

$$J \ _ \ _ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ _ \ _ int {p_g (x) f_3 (D (x)) dx}$$

जहाँ $$$f_1, f_2, f_3$ कुछ नियमों के अनुसार चुने गए हैं। वैसे, इयान गुडफेलो अपने मूल लेख में उपयोग करता है $$$f_1 और f_2$ जब एक नियमित भेदभाव करने वाले को प्रशिक्षण दिया जाता है, और $$$f_3$ प्रशिक्षण के प्रारंभिक चरण में ग्रेडिएंट्स को बेहतर बनाने के लिए चुनता है:

$$

$$f_1 \ बाएँ (x \ दाएँ) = लॉग \ बाएँ (x \ दाएँ), \ f_2 \ बाएँ (x \ दाएँ) = लॉग \ बाएँ (1 \ - \ x \ दाएँ), f_3 \ बाएँ (x \ दाएँ) = लॉग \ लेफ्ट (x \ right)$$

पहली नज़र में, कार्य धीरे-धीरे वंश (चढ़ाई) के साथ सीखने के सामान्य कार्य के समान प्रतीत होगा। फिर, GAN प्रशिक्षण में आए सभी लोग इस बात से सहमत थे कि यह कितना कठिन था?

इसका जवाब वेक्टर फ़ील्ड की संरचना में है, जिसका उपयोग हम तंत्रिका नेटवर्क के मापदंडों को अपडेट करने के लिए करते हैं। सामान्य वर्गीकरण समस्या के मामले में, हम केवल ग्रेडिएंट वेक्टर का उपयोग करते हैं, अर्थात फ़ील्ड संभावित है (स्वयं अनुकूलित वेक्टर इस वेक्टर फ़ील्ड की क्षमता है)। और संभावित वेक्टर क्षेत्रों में कुछ उल्लेखनीय गुण हैं, जिनमें से एक बंद घटता की अनुपस्थिति है। यही है, इस क्षेत्र में हलकों में चलना असंभव है। लेकिन जब जीएएन का प्रशिक्षण लिया जाता है, इस तथ्य के बावजूद कि जनरेटर और विभेदक के लिए वेक्टर क्षेत्र अलग-अलग क्षमता (समान हैं), कुल वेक्टर क्षेत्र संभावित नहीं होगा। और इसका मतलब है कि इस क्षेत्र में बंद वक्र हो सकते हैं, अर्थात हम मंडलियों में चल सकते हैं। और यह बहुत, बहुत बुरा है।

सवाल उठता है: क्यों, सभी एक ही, हम जीएएन को सफलतापूर्वक प्रशिक्षित करने के लिए प्रबंधन करते हैं, शायद क्षेत्र अभी भी इरोटिक (संभावित) है? और अगर है, तो यह इतना जटिल क्यों है?
मैं आगे चलूंगा, दुर्भाग्य से, क्षेत्र संभावित नहीं है, लेकिन इसमें कई अच्छे गुण हैं। दुर्भाग्य से, यह क्षेत्र तंत्रिका नेटवर्क (सक्रियण कार्यों की पसंद, ड्रॉपऑट, बैचैनेर्लाइजेशन, आदि का उपयोग) के मानकीकरण के लिए भी बहुत संवेदनशील है। लेकिन पहले बातें पहले।

"ढाल" गण क्षेत्र

हम सबसे सामान्य रूप में GAN सीखने की कार्यक्षमता पर विचार करेंगे:

$$

$$J \ _ \ _ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ _ \ _ int {p_g (x) f_3 (D (x)) dx}$$

हमें एक ही समय में दोनों कार्यात्मकताओं को अनुकूलित करने की आवश्यकता है। यह मानते हुए कि D (x) और pg (x) बिल्कुल लचीले कार्य हैं, अर्थात् हम अन्य बिंदुओं की परवाह किए बिना किसी भी बिंदु पर कोई भी संख्या ले सकते हैं। यह विविधताओं की गणना से एक प्रसिद्ध तथ्य है - आपको इस कार्यात्मक के परिवर्तनशील व्युत्पन्न की दिशा में फ़ंक्शन को बदलने की आवश्यकता है (सामान्य तौर पर, ढाल वृद्धि का एक पूरा एनालॉग)।

हम परिवर्तनशील व्युत्पन्न लिखते हैं:

$$

$$\ frac {\ आंशिक J} {\ आंशिक D (x)} = p_d (x) f_1 '(D (x)) \ + \ p_g (x) f_2' (D (x))$$

$$

$$\ frac {\ आंशिक I} {\ आंशिक p_g (x)} = f_3 (D (x))$$

हम केवल पहले कार्यात्मक (विवेचक के लिए) पर विचार करेंगे, दूसरे के लिए सब कुछ समान होगा।

लेकिन यह देखते हुए कि वास्तव में हम फ़ंक्शन को केवल हमारे तंत्रिका नेटवर्क द्वारा प्रतिनिधित्व करने वाले कार्यों के सेट में बदल सकते हैं, हम लिखेंगे:

$$$ $ प्रदर्शन $ $ ∆D (x) = \ frac {\ आंशिक डी (x)} {\ आंशिक ∆_j} }_j $ $ प्रदर्शन $ $

नेटवर्क मापदंडों में परिवर्तन, सामान्य तौर पर, सामान्य ढाल वंश (वृद्धि):

$$$ $ प्रदर्शन $ $ =j = \ frac {\ आंशिक J} {\ आंशिक $_j} μ $ $ प्रदर्शन $ $

rate सीखने की दर है। खैर, नेटवर्क मापदंडों के संबंध में व्युत्पन्न:

$$

$$\ frac {\ आंशिक J} {\ आंशिक \ theta_j} = \ int {\ frac {\ आंशिक J} {\ आंशिक D (y)} \ frac {\ आंशिक D (y)} {\ आंशिक \ theta_j} }$$

और अब हम इसे एक साथ रख रहे हैं:

$$

$$JD (x) = \ sum_ {j} {\ frac {\ आंशिक D (x)} {\ आंशिक \ theta_j} \ int {\ frac {\ आंशिक J} {\ आंशिक D (y)} \ "f {{ \ आंशिक डी (y)} {\ आंशिक \ theta_j} dy} \ mu \ = \ mu \ int \ frac {\ आंशिक J} {\ आंशिक D (y)}} \ sum_ {j} {\ frac \ {आंशिक D (x)} {\ आंशिक \ theta_j} \ frac {\ आंशिक D (x)} {\ आंशिक \ theta_j} dy \ = \} \ mu \ int {\ frac {\ आंशिक J} {\ आंशिक D (y) )} K_ \ थीटा (x, y) डाई}$$

जहां: $$$K_ \ the थीटा (x, y) \ = \ sum_ {j} {\ frac {\ आंशिक D (x)} {\ आंशिक \ theta_j} \ frac {\ आंशिक D (x)} {\ आंशिक \ _ta_j} \ _ }$

मैंने मशीन लर्निंग पर साहित्य में इस विशेषता को कभी नहीं देखा है, इसलिए मैं इसे सिस्टम का पैरामीट्रिक कोर कहूंगा।

ठीक है, या यदि हम समय पर निरंतर चरणों में जाते हैं (अंतर समीकरणों से अंतर तक), तो हमें मिलता है:

$$

$$\ frac {d} {dt} D (x) \ = \ int \ {frac {\ आंशिक J} {\ आंशिक D (y)} K_ \ theta (x, y) dy}$$

यह समीकरण मूल क्षेत्र (विवेचक के लिए बिंदुवार) और तंत्रिका नेटवर्क के मापदंडों के आंतरिक संबंध को दर्शाता है। हम जनरेटर के लिए पूरी तरह से समान समीकरण प्राप्त करते हैं।

यह देखते हुए कि K (x, y) (पैरामीट्रिक कर्नेल) एक सकारात्मक निश्चित कार्य है (अच्छी तरह से, इसे इसी बिंदु पर ग्रेडिएंट के स्केलर उत्पाद के रूप में कैसे दर्शाया जा सकता है), हम यह निष्कर्ष निकाल सकते हैं कि प्रशिक्षित कार्यों में कोई भी परिवर्तन (डिस्क्रिमिनेटर और जनरेटर) हिल्बर्ट स्पेस के हैं कोर द्वारा उत्पन्न, अर्थात्। के (x, y)। मुझे आश्चर्य है कि अगर यहां कोई सार्थक परिणाम प्राप्त करना संभव है। लेकिन हम अभी उस दिशा में नहीं दिखेंगे, लेकिन हम दूसरे दिशा में देखेंगे।

जैसा कि आप देख सकते हैं, GAN की स्थिरता दो घटकों द्वारा निर्धारित की जाती है: कार्यात्मक के वैरिएबल डेरिवेटिव और तंत्रिका नेटवर्क के पैरामीटर। हमारा कार्य यह देखना है कि यह फ़ील्ड पॉइंटवाइज़ कैसे व्यवहार करती है, अर्थात यदि हमारा नेटवर्क किसी भी फ़ंक्शन का प्रतिनिधित्व कर सकता है। कार्य दो-आयामी वेक्टर क्षेत्र के विश्लेषण में बदल जाता है। और यह, मुझे लगता है, हमारी शक्ति में है।

स्थिरता

तो, हम निम्नलिखित वेक्टर क्षेत्र पर विचार करते हैं:

$$

$$\ frac {d} {dt} D (x) = \ \ frac {\ आंशिक J} {\ आंशिक D (x)}$$

$$

$$\ frac {d} {dt} p_g (x) = \ \ frac {\ आंशिक I} {\ आंशिक p_g (x)}$$

स्पष्ट रूप से, इन समीकरणों को केवल एक बिंदु x के लिए माना जा सकता है, यह ध्यान में रखते हुए कि हमारा परिवर्तनशील व्युत्पन्न कैसा दिखता है:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ Prime (D) \ + \ p_gf_2 ^ \ Prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D)$$

समीकरणों की इस प्रणाली के लिए पहली आवश्यकता यह है कि दाएं हाथ के पक्षों को 0 पर जाना चाहिए:
$$$p_d = p_g$

अन्यथा, हम मॉडल को प्रशिक्षित करने की कोशिश करेंगे, जो स्पष्ट रूप से सही समाधान में नहीं जुटेगा। यानी डी निम्नलिखित समीकरण का समाधान होना चाहिए:

$$

$$f_1 ^ \ Prime (D) \ + \ f_2 ^ \ Prime (D) \ = \ 0$$

हम इस समाधान को निरूपित करते हैं $$$D0$ ।

इस तथ्य को देखते हुए कि pg (x) दाईं ओर की घनत्व घनत्व है, हम डेरिवेटिव का उल्लंघन किए बिना किसी भी संख्या को जोड़ सकते हैं। वांछित बिंदु पर दाएं हाथ के 0 प्रदान करने के लिए, टी में मूल्य घटाएं। $$$D0$ (यह तब किया जाना चाहिए जब हम pg पॉइंटवाइज़ पर विचार करना चाहते हैं - संभाव्यता घनत्व से मुक्त फ़ील्ड द्वारा परिचालित क्षेत्र से संक्रमण)।

परिणामस्वरूप, हम निम्नलिखित क्षेत्र प्राप्त करते हैं:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ Prime (D) \ + \ p_gf_2 ^ \ Prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D) \ - \ f (D0)$$

अब से, हम इस तरह के क्षेत्रों के बीच के बिंदुओं और स्थिरता का अध्ययन करेंगे।
हम दो प्रकार की स्थिरता का अध्ययन कर सकते हैं: स्थानीय (मौन बिंदु के आसपास के क्षेत्र में) और वैश्विक (लायपुनोव फ़ंक्शन विधि का उपयोग करके)।

स्थानीय स्थिरता का अध्ययन करने के लिए, जैकोबी क्षेत्र मैट्रिक्स की गणना करना आवश्यक है।
क्षेत्र के स्थानीय रूप से "स्थिर" होने के लिए यह आवश्यक है कि आइजनवेल्स का नकारात्मक वास्तविक भाग हो।

विभिन्न प्रकार के GAN

1. क्लासिक गण

   
   
   क्लासिक GAN में, हम नियमित logloss का उपयोग करते हैं:
   

   $$

   $$J \ _ \ _ int {p_d (x) लॉग (D (x)) dx \ + \ \ int {p_g (x) लॉग (1 \ - \ D (x)) dx}}$$
   
   विवेचक के प्रशिक्षण के लिए, इसे कम करने के लिए, जनरेटर के लिए, इसे अधिकतम करना आवश्यक है। इस स्थिति में, फ़ील्ड इस तरह दिखेगा:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ -log (1-D) \ + लॉग (\ frac {1} {2})$$
   
   आइए देखें कि इस क्षेत्र में पैरामीटर (पीजी और डी) कैसे विकसित होंगे। ऐसा करने के लिए, इस सरल पायथन स्क्रिप्ट का उपयोग करें:
   
   
   लिपि

   def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = -np.log(1.-d) + np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
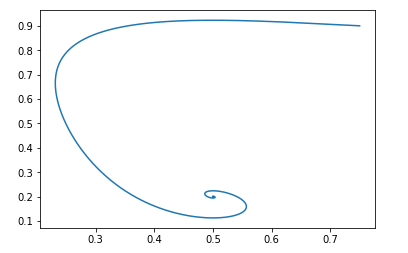
   शुरुआती बिंदु के लिए $$$p_g = 0.9, D = 0.25$ यह इस तरह दिखेगा:
   
   
   
   ऐसे क्षेत्र का बाकी बिंदु होगा: pg = pd और D = 0.5
   
   एक व्यक्ति आसानी से यह सत्यापित कर सकता है कि जैकोबी मैट्रिक्स के आइगेनवेल्यूज़ के वास्तविक हिस्से नकारात्मक हैं, अर्थात यह क्षेत्र स्थानीय रूप से स्थिर है।
   हम वैश्विक स्थिरता के प्रमाण से नहीं निपटेंगे। लेकिन अगर यह बहुत दिलचस्प है, तो आप पाइथन स्क्रिप्ट के साथ खेल सकते हैं और यह सुनिश्चित कर सकते हैं कि फ़ील्ड किसी भी मान्य प्रारंभिक मान के लिए स्थिर है।

2. जनवरी गुडफेलो द्वारा संशोधन

   
   हमने पहले ही ऊपर चर्चा की है कि मूल लेख में इयान गुडफेलो ने GAN का थोड़ा संशोधित संस्करण इस्तेमाल किया है। इसके संस्करण के लिए, कार्य निम्नानुसार थे:
   

   $$

   $$f_1 \ बाएँ (x \ दाएँ) = लॉग \ बाएँ (x \ दाएँ), \ f_2 \ बाएँ (x \ दाएँ) = लॉग \ बाएँ (1 \ - \ x \ दाएँ), f_3 \ बाएँ (x \ दाएँ) = लॉग \ लेफ्ट (x \ right)$$
   
   क्षेत्र इस तरह दिखेगा:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ log (D) \ - \ log (\ frac {1} {2})$$
   
   अजगर लिपि समान होगी, केवल फ़ील्ड फ़ंक्शन अलग है:
   
   
   लिपि

    def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = np.log(d) - np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   और उसी प्रारंभिक डेटा के साथ, चित्र इस तरह दिखता है:
   
   
   
   और फिर, यह सत्यापित करना आसान है कि क्षेत्र स्थानीय रूप से स्थिर होगा।
   यही है, अभिसरण के दृष्टिकोण से, इस तरह के संशोधन GAN के गुणों को प्रभावित नहीं करते हैं, लेकिन प्रशिक्षण तंत्रिका नेटवर्क के संदर्भ में इसके अपने फायदे हैं।

3. वासेरस्टीन गण

   
   आइए GAN के एक और लोकप्रिय दृश्य को देखें। अनुकूलित कार्यक्षमता इस तरह दिखती है:
   

   $$

   $$J \ _ \ _ int {p_d (x) D (x) dx \ - \} \ int {p_g (x) D (x) dx}$$
   
   जहाँ D का संबंध x के संबंध में 1-लिप्सचित्ज़ फ़ंक्शंस के वर्ग से है।
   हम इसे D से अधिकतम करना चाहते हैं और इसे pg द्वारा कम से कम करना चाहते हैं।
   
   जाहिर है, इस मामले में: $$$f_1 \ बाएँ (x \ दाएँ) = x, \ f_2 \ बाएँ (x \ दाएँ) = - x, \ f_3 \ बाएँ (x \ दाएँ) = x$
   
   और क्षेत्र इस तरह दिखेगा:
   

   $$

   $$\ frac {d} {dt} D = \ p_d \ - {\ p} _g \ $$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ D$$
   
   इस क्षेत्र में, एक बिंदु पर एक केंद्र के साथ एक चक्र आसानी से अनुमान लगाया जाता है। $$$p_g = p_d, D = 0$ ।
   यही है, अगर हम इस क्षेत्र में जाते हैं, तो हम हमेशा हलकों में घूमेंगे।
   
   इस तरह के क्षेत्र में एक प्रक्षेपवक्र का एक उदाहरण है:
   
   
   
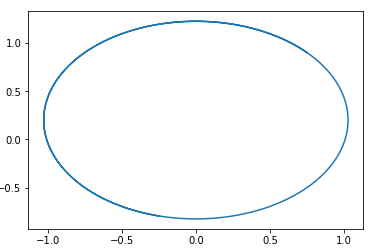
   सवाल यह है कि फिर इस तरह के गण को प्रशिक्षित करने की बात क्यों? इसका उत्तर बहुत सरल है - यह विश्लेषण डी। के 1-लिप्सकैट संपत्ति के तथ्य को ध्यान में नहीं रखता है। अर्थात, हम मनमाने कार्य नहीं कर सकते। वैसे, यह लेख के परिणामों के साथ अच्छा है ... लेख का। एक मंडली में चलने से बचने के लिए, वे विवेचक को रूपांतरित करने के लिए प्रशिक्षण देने की सलाह देते हैं: वासेरस्टीन जीएएन

4. नई गण विकल्प

   
   फ़ीचर चयन $$$f_1, f_2 और f_3$ आप विभिन्न GAN विकल्प बना सकते हैं। इन कार्यों के लिए मुख्य आवश्यकता एक "सही" आराम बिंदु की उपस्थिति और इस बिंदु की स्थिरता (अधिमानतः वैश्विक, लेकिन कम से कम स्थानीय) सुनिश्चित करना है। मैं पाठक को स्थानीय स्थिरता के लिए आवश्यक, f1, f2 और f3 के कार्यों पर प्रतिबंध लगाने का अवसर देता हूं। यह आसान है - बस जैकोबी मैट्रिक्स के आइगेनवेल्स के लिए द्विघात समीकरण पर विचार करें।
   
   मैं ऐसे GAN का एक उदाहरण दूंगा:
   

   $$

   $$f_1 (x) \ = \ -0.5x ^ 2, \ f_2 (x) \ = \ x, \ f_3 (x) \ = \ -x$$
   
   फिर से, मेरा सुझाव है कि पाठक स्वयं इस GAN के क्षेत्र का निर्माण करें और इसकी स्थिरता को साबित करें। (वैसे, यह उन कुछ क्षेत्रों में से एक है, जिसके लिए वैश्विक स्थिरता का प्रमाण प्राथमिक है - बस ल्यपुनोव फ़ंक्शन का चयन करें, आराम बिंदु की दूरी)। बस ध्यान रखें कि बाकी बिंदु D = 1 है।

निष्कर्ष और आगे का शोध

उपरोक्त विश्लेषण से यह देखा जा सकता है कि सभी शास्त्रीय GAN (वासेरेटिन GAN के अपवाद के साथ, जिसमें स्थिरता में सुधार के लिए अपने तरीके हैं) में "अच्छे" क्षेत्र हैं। यानी इन क्षेत्रों के बाद एक एकल विश्राम बिंदु है जिस पर जनरेटर का वितरण डेटा के वितरण के बराबर है।

फिर, GAN को प्रशिक्षित करना इतना मुश्किल काम क्यों है। इसका उत्तर सरल है - तंत्रिका नेटवर्क का मानकीकरण। एक "खराब" पैरामीटराइजेशन के साथ, हम सर्कल में वॉक के लिए भी जा सकते हैं। उदाहरण के लिए, मेरे प्रयोगों से पता चलता है कि, उदाहरण के लिए, किसी भी नेटवर्क में बैचनलाइज़ेशन का उपयोग करके फ़ील्ड को तुरंत बंद कर दिया जाता है। और Relu सक्रियण सबसे अच्छा काम करता है।

दुर्भाग्य से, फिलहाल सैद्धांतिक रूप से यह जांचने का एक तरीका नहीं है कि तंत्रिका नेटवर्क के कौन से तत्व फ़ील्ड को कैसे बदलें। यह मेरे लिए सिस्टम के पैरामीट्रिक कर्नेल के गुणों की जांच करने के लिए संभावित साबित होगा - $$$K_ \ थीटा (x, y)$ ।

मैं GAN क्षेत्रों को नियमित करने के तरीकों के बारे में और दो-आयामी क्षेत्रों के दृष्टिकोण से इस पर एक नज़र डालना चाहता था। इस दृष्टिकोण से सुदृढीकरण सीखने के एल्गोरिदम पर विचार करें। और भी बहुत कुछ। लेकिन दुर्भाग्य से, लेख वैसे भी बहुत बड़ा निकला, इसलिए कुछ और समय के बारे में।