कई सालों से मैं स्नूकर को एक खेल के रूप में देखता रहा हूं। इसके पास सब कुछ है: एक बौद्धिक खेल की शानदार सुंदरता, कीम स्ट्रोक की सुंदरता और प्रतिस्पर्धा का मनोवैज्ञानिक तनाव। लेकिन एक चीज है जो मुझे पसंद नहीं है - इसकी रेटिंग प्रणाली ।
इसका मुख्य दोष यह है कि यह केवल मैचों की "जटिलता" को ध्यान में रखे बिना टूर्नामेंट की उपलब्धि के तथ्य को ध्यान में रखता है। एलो मॉडल इस खामी से वंचित है, जो खिलाड़ियों की "ताकत" पर नज़र रखता है और मैचों के परिणामों और प्रतिद्वंद्वी की "ताकत" के आधार पर इसे अपडेट करता है। हालांकि, यह पूरी तरह से फिट नहीं है: यह माना जाता है कि सभी मैच समान परिस्थितियों में आयोजित किए जाते हैं, और स्नूकर में वे एक निश्चित संख्या में जीते हुए फ्रेम (पार्टियों) तक खेले जाते हैं। इस तथ्य के लिए, मैंने एक और मॉडल पर विचार किया, जिसे मैंने एलोबेटा कहा।
यह लेख स्नूकर मैचों के परिणामों के आधार पर एलो और एलोबेट मॉडल की गुणवत्ता का अध्ययन करता है। यह ध्यान रखना महत्वपूर्ण है कि मुख्य लक्ष्य खिलाड़ियों की "ताकत" का आकलन करना और लाभ प्राप्त करने के लिए पूर्वानुमान मॉडल के निर्माण के बजाय "निष्पक्ष" रेटिंग बनाना है।

वर्तमान स्नूकर रेटिंग टूर्नामेंट में खिलाड़ी की उपलब्धियों के आधार पर उनके अलग-अलग "वजन" पर आधारित है। एक बार, केवल विश्व चैंपियनशिप को ध्यान में रखा गया था। कई अन्य प्रतियोगिताओं की उपस्थिति के बाद, अंक तालिका विकसित की गई थी कि खिलाड़ी टूर्नामेंट के एक निश्चित चरण में पहुंचने पर कमा सकता है। अब रेटिंग में पुरस्कार राशि के "चलती" राशि का रूप है जो खिलाड़ी ने पिछले दो कैलेंडर वर्षों के दौरान (लगभग) अर्जित किया है।
इस प्रणाली के दो मुख्य फायदे हैं: यह सरल है (बहुत सारा पैसा जीतना - रैंकिंग में ऊपर जाना) और पूर्वानुमेय (यदि आप एक निश्चित स्थान तक जाना चाहते हैं - एक निश्चित राशि जीतें, अन्य सभी चीजें समान हो रही हैं)। समस्या यह है कि इस पद्धति के साथ विरोधियों की ताकत (कौशल, रूप) को ध्यान में नहीं रखा जाता है । सामान्य प्रतिवाद है: "यदि कोई खिलाड़ी टूर्नामेंट के अंतिम चरण में पहुंच गया है, तो वह वर्तमान मजबूत खिलाड़ी की परिभाषा में है" ("कमजोर खिलाड़ी टूर्नामेंट नहीं जीतते")। सुनने में बहुत अच्छा लगता है। हालांकि, स्नूकर में, किसी भी खेल में, मामले की भूमिका को ध्यान में रखा जाना चाहिए: यदि कोई खिलाड़ी "कमजोर" है, तो इसका मतलब यह नहीं है कि वह / वह कभी भी एक खिलाड़ी के खिलाफ मैच में "मजबूत" नहीं जीत सकता है। यह रिवर्स परिदृश्य की तुलना में अक्सर कम होता है। यह वह जगह है जहाँ एलो मॉडल दृश्य पर आता है।
एलो मॉडल का विचार यह है कि प्रत्येक खिलाड़ी एक संख्यात्मक रेटिंग के साथ जुड़ा हुआ है। एक धारणा पेश की गई है कि दो खिलाड़ियों के बीच के खेल के परिणाम का अनुमान उनकी रेटिंग में अंतर के आधार पर लगाया जा सकता है: उच्च मूल्यों का अर्थ है "मजबूत" (उच्च रेटिंग के साथ) खिलाड़ी जीतने की उच्च संभावना। एलो रेटिंग वर्तमान "ताकत" पर आधारित है, जिसकी गणना अन्य खिलाड़ियों के साथ मैचों के परिणामों के आधार पर की जाती है। यह वर्तमान आधिकारिक रेटिंग प्रणाली में एक प्रमुख दोष से बचा जाता है। यह दृष्टिकोण आपको टूर्नामेंट के दौरान खिलाड़ी के रेटिंग को अपडेट करने की अनुमति देता है ताकि उसके अच्छे प्रदर्शन के लिए संख्यात्मक रूप से जवाब दिया जा सके।
एलो रेटिंग के साथ व्यावहारिक अनुभव होने के बाद, यह मुझे लगता है कि स्नूकर में खुद को अच्छा दिखाना चाहिए। हालांकि, एक बाधा है: यह एक ही प्रकार के मैच के साथ प्रतियोगिताओं के लिए डिज़ाइन किया गया है । बेशक, फुटबॉल में घरेलू मैदान के फायदे और शतरंज में पहली चाल (दोनों खिलाड़ी एक लाभ के साथ खिलाड़ी को एक निश्चित संख्या में रेटिंग अंक जोड़ने के रूप में) में बदलाव करते हैं। स्नूकर में, मैच "सर्वश्रेष्ठ एन" प्रारूप में खेले जाते हैं: जो खिलाड़ी पहले जीतता है n= fracN+12 फ्रेम (पार्टी)। हम इस प्रारूप को "जब तक" भी कहेंगे एन जीत। "
सहज रूप से, 10 जीत (एक गंभीर टूर्नामेंट के फाइनल) तक एक मैच जीतना "कमजोर" खिलाड़ी के लिए 4 जीत (वर्तमान गृह राष्ट्र टूर्नामेंट के पहले दौर) का मैच जीतने से अधिक कठिन होना चाहिए। यह मेरे एलोबेट मॉडल में ध्यान में रखा गया है।
स्नूकर में एलो रेटिंग का उपयोग करने का विचार कोई नया नहीं है। उदाहरण के लिए, निम्नलिखित कार्य हैं:
- स्नूकर विश्लेषक "एलो लाइक" ( ब्रैडली - टेरी मॉडल की तरह ) रेटिंग प्रणाली का उपयोग करता है। यह विचार "वास्तविक" और "अपेक्षित" संख्या के बीच अंतर के आधार पर रेटिंग को अद्यतन करने के लिए जीता गया है। यह दृष्टिकोण सवाल उठाता है। बेशक, फ़्रेम की संख्या में बड़ा अंतर सबसे अधिक संभावना है कि ताकत में अधिक अंतर दिखाई देता है, लेकिन शुरू में खिलाड़ी के पास ऐसा कोई कार्य नहीं होता है। स्नूकर में, मैच जीतने के लिए लक्ष्य "बस" है, अर्थात। प्रतिद्वंद्वी से पहले फ्रेम की एक निश्चित संख्या जीतें।
- यह चर्चा बुनियादी एलो मॉडल के कार्यान्वयन के साथ मंच पर है ।
- यह और ये शौकिया स्नूकर में वास्तविक उपयोग हैं ।
- शायद अन्य काम हैं जो मुझे याद आए। मैं इस विषय पर किसी भी जानकारी के लिए बहुत आभारी रहूंगा।
सिंहावलोकन
यह लेख आर भाषा के उपयोगकर्ताओं के लिए अभिप्रेत है जो एलो की रेटिंग का अध्ययन करने और स्नूकर के प्रशंसकों के लिए रुचि रखते हैं। सभी प्रयोग प्रजनन योग्य होने के विचार से लिखे गए हैं। कोड को स्पॉइलर के नीचे छिपाया गया है, टिप्पणी है और tidyverse पैकेज का उपयोग करता है, इसलिए उपयोगकर्ताओं के लिए स्वयं आर द्वारा पढ़ना दिलचस्प हो सकता है। यह माना जाता है कि प्रस्तुत सभी कोड क्रमिक रूप से निष्पादित किए जाते हैं। एक फाइल यहां मिल सकती है ।
लेख इस प्रकार है:
- मॉडल अनुभाग आर में कार्यान्वयन के साथ एलो और एलोबेट के दृष्टिकोण का वर्णन करता है।
- प्रयोग अनुभाग गणना के विवरण और प्रेरणा का वर्णन करता है: क्या डेटा और कार्यप्रणाली का उपयोग किया जाता है (और क्यों), और क्या परिणाम प्राप्त होते हैं।
- एलोबेट रैंकिंग अध्ययन अनुभाग में वास्तविक स्नूकर डेटा के लिए एलोबेट मॉडल को लागू करने के परिणाम हैं। वह स्नूकर प्रेमियों में अधिक रुचि लेंगे।
हमें निम्नलिखित आरंभ की आवश्यकता होगी।
प्रारंभिक कोड# suppressPackageStartupMessages(library(dplyr)) library(tidyr) library(purrr) # library(ggplot2) # suppressPackageStartupMessages(library(comperank)) theme_set(theme_bw()) # . . set.seed(20180703)
आदर्श
दोनों मॉडल निम्नलिखित मान्यताओं पर आधारित हैं:
- खिलाड़ियों का एक निश्चित सेट है जिसे "सबसे मजबूत" (पहली जगह) से "सबसे कमजोर" (अंतिम स्थान) पर रैंक किया जाना चाहिए।
- खिलाड़ी संघ द्वारा रैंकिंग मैं संख्यात्मक रेटिंग के साथ ri : खिलाड़ी की "ताकत" (एक उच्च मूल्य का अर्थ एक मजबूत खिलाड़ी) का प्रतिनिधित्व करने वाली संख्या है।
- मैच से पहले रेटिंग में अंतर जितना अधिक होगा, "कमजोर" खिलाड़ी की जीत की संभावना कम होगी (कम रेटिंग के साथ)।
- इसके परिणाम के आधार पर और उसके पहले की रेटिंग के आधार पर रेटिंग्स को अपडेट किया जाता है।
- एक प्रतिद्वंद्वी "मजबूत" पर जीत एक प्रतिद्वंद्वी "कमजोर" पर जीत की तुलना में रेटिंग में बड़ी वृद्धि के साथ होनी चाहिए। हार के साथ, विपरीत सच है।
एलो
एलो मॉडल कोड #' @details . #' `...` . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). #' . elo_win_prob <- function(rating1, rating2, ksi = 400, ...) { norm_rating_diff <- (rating2 - rating1) / ksi 1 / (1 + 10^norm_rating_diff) } #' @return , #' `comperank::add_iterative_ratings()`. elo_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { comperank::elo(rating1, score1, rating2, score2, K = K, ksi = ksi)[1, ] } }
एलो मॉडल निम्नलिखित प्रक्रिया द्वारा रेटिंग अपडेट करता है:
मैच जीतने से पहले एक निश्चित खिलाड़ी की संभावना की गणना (शुरू होने से पहले)। पहचानकर्ता के साथ एक खिलाड़ी के जीतने की संभावना (हम उसे / उसे "पहले" कहेंगे) मैं और रेट किया गया ri पहचानकर्ता के साथ एक और खिलाड़ी ("दूसरा") ज और रेट किया गया rj बराबरी
Pr(ri,rj)= frac11+10(rj−ri)/400
इस दृष्टिकोण के साथ, संभाव्यता की गणना तीसरी धारणा का पालन करती है।
400 के अंतर को सामान्य करना यह कहने का गणितीय तरीका है कि किस अंतर को "बड़ा" माना जाता है। इस नंबर को मॉडल पैरामीटर से बदला जा सकता है। xi हालांकि, यह केवल भविष्य की रेटिंग के प्रसार को प्रभावित करता है और आमतौर पर बेमानी है। 400 का मान काफी मानक है।
एक सामान्य दृष्टिकोण के साथ, जीत की संभावना बराबर होती है L(rj−ri) जहाँ L(x) 0 से 1. मान के साथ कुछ सख्ती से बढ़ते कार्य। हम लॉजिस्टिक वक्र का उपयोग करेंगे। इस लेख में एक अधिक संपूर्ण अध्ययन पाया जा सकता है।
मैच परिणाम गणना एस । बेस मॉडल में, यह पहले खिलाड़ी की जीत के मामले में 1 (दूसरे की हार) के बराबर है, ड्रॉ की स्थिति में 0.5 और पहले खिलाड़ी की हार के मामले में 0 है (दूसरे की जीत)।
रेटिंग अपडेट :
- delta=K cdot(S−Pr(ri,rj)) । यह वह राशि है जिसके द्वारा रेटिंग बदल जाएगी। वह एक गुणांक का उपयोग करता है K (मॉडल का एकमात्र पैरामीटर)। कम K (समान संभावनाओं के साथ) का अर्थ है कि रेटिंग में थोड़ा बदलाव - मॉडल अधिक रूढ़िवादी है, अर्थात्। ताकत में बदलाव को "साबित" करने के लिए अधिक जीत की आवश्यकता है। दूसरी ओर, अधिक K वर्तमान रेटिंग की तुलना में हाल के परिणामों के साथ अधिक विश्वसनीयता का मतलब है। "इष्टतम" का विकल्प K एक "अच्छा" रेटिंग सिस्टम बनाने का एक तरीका है ।
- r(new)i=ri+ delta । r(new)j=rj− delta ।
टिप्पणी :
- जैसा कि अपडेट फ़ार्मुलों से देखा जा सकता है, सभी माने गए खिलाड़ियों की रेटिंग का योग समय के साथ नहीं बदलता है: प्रतिद्वंद्वी की रेटिंग में कमी के कारण रेटिंग बढ़ती है
- बिना खेले मैच खेले जाने वाले खिलाड़ी 0. की प्रारंभिक रेटिंग के साथ जुड़े होते हैं। आमतौर पर, 1500 या 1000 के मूल्यों का उपयोग किया जाता है, लेकिन मुझे मनोवैज्ञानिक के अलावा और कोई कारण नहीं दिखता है। पिछली टिप्पणी को ध्यान में रखते हुए, शून्य का उपयोग करने का मतलब है कि सभी रेटिंग का योग हमेशा शून्य होता है, जो अपने तरीके से सुंदर होता है।
- रेटिंग के लिए खिलाड़ी की "ताकत" को दर्शाने के लिए निश्चित संख्या में मैच खेलना आवश्यक है। यह एक समस्या प्रस्तुत करता है: नए जोड़े गए खिलाड़ी 0 की रेटिंग के साथ शुरू होते हैं, जो शायद वर्तमान खिलाड़ियों में सबसे छोटा नहीं है। दूसरे शब्दों में, "नवागंतुकों" को कुछ अन्य खिलाड़ियों की तुलना में "अधिक मजबूत" माना जाता है। किसी नए खिलाड़ी को दर्ज करते समय आप बाहरी रेटिंग अपडेट प्रक्रियाओं के साथ इससे लड़ने की कोशिश कर सकते हैं।
इस तरह के एक एल्गोरिथ्म क्यों समझ में आता है? रेटिंग की समानता के मामले में डेल्टा हमेशा बराबरी करता है 0.5 cdotK । उदाहरण के लिए मान लीजिए कि ri=0 और rj=400 । इसका मतलब है कि पहले खिलाड़ी के जीतने की संभावना है frac11+10 लगभग0.0909 , यानी। वह 11 में से 1 मैच जीतेगा।
- जीत के मामले में, उसे लगभग वृद्धि प्राप्त होगी 0.909 cdotK , जो रेटिंग की समानता के मामले में अधिक है।
- हार की स्थिति में, उसे लगभग कमी प्राप्त होगी 0.0909 cdotK , जो रेटिंग की समानता के मामले में कम है।
इससे पता चलता है कि एलो मॉडल पांचवीं धारणा का पालन करता है: एक प्रतिद्वंद्वी पर जीत "मजबूत" होती है और साथ में एक प्रतिद्वंद्वी पर जीत की तुलना में रेटिंग में बड़ी वृद्धि होती है "कमजोर", और इसके विपरीत।
बेशक, एलो मॉडल की अपनी (बल्कि उच्च-स्तरीय) व्यावहारिक विशेषताएं हैं । हालांकि, हमारे अध्ययन के लिए सबसे महत्वपूर्ण निम्नलिखित है: यह माना जाता है कि सभी मैच एक समान स्तर पर होते हैं। इसका मतलब यह है कि मैच की दूरी को ध्यान में नहीं रखा जाता है: 4 जीत तक के मैच में जीत उसी तरह से मिलती है, जैसे 10 जीत तक के मैच में जीत। यहां मंच मॉडल एलोबेटा आता है।
EloBeta
एलोबेट मॉडल कोड #' @details . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). `frames_to_win` #' . #' . elobeta_win_prob <- function(rating1, rating2, frames_to_win, ksi = 400, ...) { prob_frame <- elo_win_prob(rating1 = rating1, rating2 = rating2, ksi = ksi) # , `frames_to_win` # # (`prob_frame`). . pbeta(prob_frame, frames_to_win, frames_to_win) } #' @return : 1 / #' (), 0.5 0 / (). get_match_result <- function(score1, score2) { # () , . near_score <- dplyr::near(score1, score2) dplyr::if_else(near_score, 0.5, as.numeric(score1 > score2)) } #' @return , #' `add_iterative_ratings()`. elobeta_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { prob_win <- elobeta_win_prob( rating1 = rating1, rating2 = rating2, frames_to_win = pmax(score1, score2), ksi = ksi ) match_result <- get_match_result(score1, score2) delta <- K * (match_result - prob_win) c(rating1 + delta, rating2 - delta) } }
एलो मॉडल में, रेटिंग का अंतर सीधे पूरे मैच को जीतने की संभावना को प्रभावित करता है। एलोबेट मॉडल का मुख्य विचार एक फ्रेम में जीतने की संभावना पर रेटिंग में अंतर का सीधा प्रभाव है और एक खिलाड़ी के जीतने की संभावना की स्पष्ट गणना है एन प्रतिद्वंद्वी से पहले फ्रेम ।
सवाल यह है: ऐसी संभावना की गणना कैसे करें? यह पता चला है कि यह संभाव्यता सिद्धांत के इतिहास में सबसे पुरानी समस्याओं में से एक है और इसका अपना नाम है - विभाजित करने की समस्या (अंकों की समस्या)। इस लेख में एक बहुत अच्छी प्रस्तुति मिल सकती है। इसके अंकन का उपयोग, वांछित संभावना है:
P(n,n)= sum limit2n−1j=n2n−1 jpj(1−p)2n−1−j
यहां पी(एन,एन) - पहले खिलाड़ी के मैच जीतने की संभावना एन जीत; पी - एक फ्रेम में उसकी / उसकी जीत की संभावना (प्रतिद्वंद्वी में संभावना है 1−पी )। इस दृष्टिकोण के साथ, यह माना जाता है कि मैच के भीतर फ्रेम परिणाम एक दूसरे से स्वतंत्र हैं । यह संदेह में हो सकता है, लेकिन इस मॉडल के लिए एक आवश्यक धारणा है।
क्या गणना करने का एक तेज़ तरीका है? यह जवाब हां है। सूत्र रूपांतरण, व्यावहारिक प्रयोगों और इंटरनेट खोजों के कई घंटों के बाद, मुझे नियमित रूप से अपूर्ण बीटा फ़ंक्शन पर निम्नलिखित संपत्ति मिली Ix(ए,बी) । स्थानापन्न m=k, n=2k−1 इस संपत्ति में और जगह k पर एन यह पता चला है P(n,n)=Ip(n,n) ।
आर उपयोगकर्ताओं के लिए भी यह अच्छी खबर है Ip(n,n) pbeta(p, n, n) रूप में गणना की जा सकती है। नोट : में जीत की संभावना का सामान्य मामला एन प्रतिद्वंद्वी के जीतने से पहले फ्रेम एम के रूप में भी गणना की जा सकती है Ip(n,m) और pbeta(p, n, m) क्रमशः। यह मैच के दौरान जीतने की संभावना को अद्यतन करने के महान अवसरों को खोलता है।
एलोबेट मॉडल के ढांचे के भीतर रेटिंग अपडेट प्रक्रिया में निम्न रूप हैं (ज्ञात रेटिंग के साथ ri और rj जीतने के लिए आवश्यक फ़्रेमों की संख्या एन और मैच का परिणाम है एस , एलो मॉडल में):
- एक फ्रेम में पहले खिलाड़ी की जीत की संभावना की गणना : p=Pr(ri,rj)= frac11+10(rj−ri)/400 ।
- मैच में इस खिलाड़ी की जीत की संभावना की गणना : Prबीटा(ri,rj)=Ip(n,n) । उदाहरण के लिए, यदि पी 0.4 के बराबर, फिर 4 जीत से पहले मैच जीतने की संभावना 0.29 हो जाती है, और "18 जीत में" - 0.11 तक।
- रेटिंग अपडेट :
- delta=K cdot(S−PrBeta(ri,rj)) ।
- r(new)i=ri+ delta । r(new)j=rj− delta ।
नोट : क्योंकि रेटिंग में अंतर सीधे एक फ्रेम में जीतने की संभावना को प्रभावित करता है, और पूरे मैच में नहीं, एक कम इष्टतम गुणांक मूल्य की उम्मीद की जानी चाहिए K : मूल्य का हिस्सा डेल्टा एक मजबूत प्रभाव से आता है Prबीटा(ri,rj) ।
एक फ्रेम में जीतने की संभावना के आधार पर एक मैच के परिणाम की गणना करने का विचार बहुत नया नहीं है। फ्रांकोइस लाबेले द्वारा इस साइट पर, आप "सर्वश्रेष्ठ" जीतने की संभावना की एक ऑनलाइन गणना पा सकते हैं एन "मैच, अन्य कार्यों के साथ। मुझे यह देखकर खुशी हुई कि हमारी गणना के परिणाम मेल खाते हैं। हालांकि, एलो रेटिंग के लिए अद्यतन प्रक्रिया के लिए इस तरह के दृष्टिकोण को पेश करने के लिए मुझे कोई स्रोत नहीं मिला। पहले की तरह, मैं इस विषय की किसी भी जानकारी के लिए बहुत आभारी रहूंगा।
मैं बैकगैमौन गेम सर्वर (FIBS) पर केवल एलो सिस्टम के इस लेख और विवरण को पा सकता हूं। एक रूसी भाषा का एनालॉग भी है । यहां, मैच दूरी के वर्गमूल द्वारा रेटिंग में अंतर को गुणा करके विभिन्न मैच अवधि को ध्यान में रखा जाता है। हालाँकि, इसका कोई सैद्धांतिक औचित्य नहीं है।
एक प्रयोग
एक प्रयोग के कई लक्ष्य हैं। स्नूकर मैचों के परिणामों के आधार पर:
- सबसे अच्छा गुणांक मान निर्धारित करें K दोनों मॉडल के लिए।
- भविष्यवाणी की संभावना की सटीकता के संदर्भ में मॉडल की स्थिरता का अध्ययन करना।
- रेटिंग पर "निमंत्रण" टूर्नामेंट का उपयोग करने के प्रभाव का अध्ययन करने के लिए।
- सभी पेशेवर खिलाड़ियों के लिए 2017/18 सीज़न के लिए उचित रेटिंग इतिहास बनाएं।
डेटा
प्रयोग डेटा जनरेशन कोड # "train", "validation" "test" split_cases <- function(n, props = c(0.5, 0.25, 0.25)) { breaks <- n * cumsum(head(props, -1)) / sum(props) id_vec <- findInterval(seq_len(n), breaks, left.open = TRUE) + 1 c("train", "validation", "test")[id_vec] } pro_players <- snooker_players %>% filter(status == "pro") # pro_matches_all <- snooker_matches %>% # filter(!walkover1, !walkover2) %>% # semi_join(y = pro_players, by = c(player1Id = "id")) %>% semi_join(y = pro_players, by = c(player2Id = "id")) %>% # 'season' left_join( y = snooker_events %>% select(id, season), by = c(eventId = "id") ) %>% # arrange(endDate) %>% # widecr transmute( game = seq_len(n()), player1 = player1Id, score1, player2 = player2Id, score2, matchId = id, endDate, eventId, season, # ("train", "validation" "test") # 50/25/25 matchType = split_cases(n()) ) %>% # widecr as_widecr() # (, # , Championship League). pro_matches_off <- pro_matches_all %>% anti_join( y = snooker_events %>% filter(type == "Invitational"), by = c(eventId = "id") ) # get_split <- . %>% count(matchType) %>% mutate(share = n / sum(n)) # 50/25/25 (train/validation/test) pro_matches_all %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 1030 0.250 ## 2 train 2059 0.5 ## 3 validation 1029 0.250 # , # . , # __ __, `pro_matches_all`. # , __ # __. pro_matches_off %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 820 0.225 ## 2 train 1810 0.497 ## 3 validation 1014 0.278 # K k_grid <- 1:100
हम स्नूकर डेटा का उपयोग कॉम्पर्कैंक पैकेज से करेंगे। मूल स्रोत snooker.org है । परिणाम निम्नलिखित मैचों से लिए गए हैं:
- यह मैच 2016/17 या 2017/18 सीज़न में खेला गया था।
- मैच एक "पेशेवर" स्नूकर टूर्नामेंट का हिस्सा है , जो है:
- यह "आमंत्रण", "योग्यता", या "रैंकिंग" प्रकार का है। हम मैचों के दो सेटों को भी भेद करेंगे: "सभी मैच" (इन सभी टूर्नामेंटों से) और "आधिकारिक मैचों" (आमंत्रण टूर्नामेंटों को छोड़कर)। इसके दो कारण हैं:
- आमंत्रण टूर्नामेंट में, सभी खिलाड़ियों को अपनी रेटिंग बदलने का अवसर नहीं मिलता है। यह एलो और एलोबेट मॉडल के ढांचे के भीतर आवश्यक रूप से खराब नहीं है, लेकिन इसमें "अन्याय का तंज" है।
- ऐसी धारणा है कि खिलाड़ी केवल आधिकारिक रेटिंग मैचों के लिए "गंभीरता से लेते हैं"। नोट : अधिकांश आमंत्रण टूर्नामेंट चैम्पियनशिप लीग का हिस्सा हैं, जो मुझे लगता है कि अधिकांश खिलाड़ियों द्वारा स्वीकार किया जाता है।
बहुत गंभीरता से नहीं पैसे बनाने की क्षमता के साथ अभ्यास के रूप में। इन टूर्नामेंटों की उपस्थिति रैंकिंग को प्रभावित कर सकती है। "चैम्पियनशिप लीग" के अलावा अन्य आमंत्रण टूर्नामेंट भी हैं: "2016 चीन चैंपियनशिप", दोनों "चैंपियंस ऑफ चैंपियंस", दोनों "मास्टर्स", "2017 हांगकांग मास्टर्स", "2017 वर्ल्ड गेम्स", "2017 रोमानियाई मास्टर्स"।
- व्यक्तिगत खिलाड़ियों (टीमों के बीच नहीं) के बीच एक पारंपरिक स्नूकर (6 रेड्स या पावर स्नूकर नहीं) का वर्णन करता है।
- दोनों लिंग शामिल हो सकते हैं (न केवल पुरुष या महिला)।
- सभी उम्र के खिलाड़ी भाग ले सकते हैं (न केवल वरिष्ठ या "21 वर्ष से कम")।
- यह "शूट-आउट" नहीं है क्योंकि ये टूर्नामेंट अन्यथा snooker.org डेटाबेस में संग्रहीत किए जाते हैं।
- मैच वास्तव में हुआ : इसका परिणाम दोनों खिलाड़ियों को शामिल करने वाले वास्तविक खेल का परिणाम है।
- मैच दो पेशेवरों के बीच आयोजित किया जाता है। पेशेवरों की सूची 2017/18 सीज़न (131 खिलाड़ियों) के लिए ली गई है। यह निर्णय सबसे विवादास्पद लगता है शौकिया से पेशेवरों की हार के लिए शौकिया "अंधा" वाले मैचों को हटाने। इससे इन खिलाड़ियों को अनुचित लाभ होता है। मुझे ऐसा लगता है कि इस तरह का निर्णय रेटिंग मुद्रास्फीति को कम करने के लिए आवश्यक है जो कि शौकीनों के साथ खाते में लेने पर होता है। एक और दृष्टिकोण पेशेवरों और एमेच्योर का एक साथ अध्ययन करना है, लेकिन यह इस अध्ययन के ढांचे में अनुचित लगता है। एक पेशेवर शौकिया की हार को रेटिंग बढ़ाने के अवसर का नुकसान माना जाता है।
उपयोग किए गए मैचों की अंतिम संख्या "सभी मैचों" के लिए 4118 और "आधिकारिक मैचों" के लिए 3644 (क्रमशः 62.9 और 55.6 प्रति खिलाड़ी) है।
कार्यप्रणाली
प्रयोग समारोह कोड #' @param matches `longcr` `widecr` `matchType` #' ( : "train", "validation" "test"). #' @param test_type . #' #' ("") . , #' `game`. #' @param k_vec K . #' @param rate_fun_gen , K #' `add_iterative_ratings()`. #' @param get_win_prob #' (`rating1`, `rating2`) , #' (`frames_to_win`). ____: #' . #' @param initial_ratings #' `add_iterative_ratings()`. #' #' @details : #' - `matches` #' `game`. #' - `test_type`: #' - 1. #' - : 1 / #' (), 0.5 0 / (). #' - RMSE: , #' "" - . #' #' @return Tibble 'k' K 'goodness' #' RMSE. compute_goodness <- function(matches, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings = 0) { cat("\n") map_dfr(k_vec, function(cur_k) { # cat(cur_k, " ") matches %>% arrange(game) %>% add_iterative_ratings( rate_fun = rate_fun_gen(cur_k), initial_ratings = initial_ratings ) %>% left_join(y = matches %>% select(game, matchType), by = "game") %>% filter(matchType %in% test_type) %>% mutate( # framesToWin = pmax(score1, score2), # 1 `framesToWin` winProb = get_win_prob( rating1 = rating1Before, rating2 = rating2Before, frames_to_win = framesToWin ), result = get_match_result(score1, score2), squareError = (result - winProb)^2 ) %>% summarise(goodness = sqrt(mean(squareError))) }) %>% mutate(k = k_vec) %>% select(k, goodness) } #' `compute_goodness()` compute_goodness_wrap <- function(matches_name, test_type, k_vec, rate_fun_gen_name, win_prob_fun_name, initial_ratings = 0) { matches_tbl <- get(matches_name) rate_fun_gen <- get(rate_fun_gen_name) get_win_prob <- get(win_prob_fun_name) compute_goodness( matches_tbl, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings ) } #' #' #' @param test_type `test_type` ( ) #' `compute_goodness()`. #' @param rating_type ( ). #' @param data_type . #' @param k_vec,initial_ratings `compute_goodness()`. #' #' @details #' . #' , , #' : #' - "pro_matches_" + `< >` + `< >` . #' - `< >` + "_fun_gen" . #' - `< >` + "_win_prob" , #' . #' #' @return Tibble : #' - __testType__ <chr> : . #' - __ratingType__ <chr> : . #' - __dataType__ <chr> : . #' - __k__ <dbl/int> : K. #' - __goodness__ <dbl> : . do_experiment <- function(test_type = c("validation", "test"), rating_type = c("elo", "elobeta"), data_type = c("all", "off"), k_vec = k_grid, initial_ratings = 0) { crossing( testType = test_type, ratingType = rating_type, dataType = data_type ) %>% mutate( dataName = paste0("pro_matches_", testType, "_", dataType), kVec = rep(list(k_vec), n()), rateFunGenName = paste0(ratingType, "_fun_gen"), winProbFunName = paste0(ratingType, "_win_prob"), initialRatings = rep(list(initial_ratings), n()), experimentData = pmap( list(dataName, testType, kVec, rateFunGenName, winProbFunName, initialRatings), compute_goodness_wrap ) ) %>% unnest(experimentData) %>% select(testType, ratingType, dataType, k, goodness) }
"" K K=1,2,...,100 । , . :
- K :
- . , .
add_iterative_ratings() comperank . " ", .. . - , ( ) , . RMSE ( ) ( ). , RMSE=√1|T|∑t∈T(St−Pt)2 जहाँ T — , |T| — , St — , Pt — ( ). , " " .
- K RMSE . "" , RMSE K ( ). 0.5 ( "" 0.5) .
, : "train" (), "validation" () "test" (). , .. "train"/"validation" , "validation"/"test". 50/25/25 " ". " " " " . : 49.7/27.8/22.5. , , .
:
- : .
- : " " " " ( ". ").
- : "" ( "validation" RMSE "" "train" ) "" ( "test" RMSE "" "train" "validation" ).
परिणाम
pro_matches_validation_all <- pro_matches_all %>% filter(matchType != "test") pro_matches_validation_off <- pro_matches_off %>% filter(matchType != "test") pro_matches_test_all <- pro_matches_all pro_matches_test_off <- pro_matches_off
# experiment_tbl <- do_experiment()
plot_data <- experiment_tbl %>% unite(group, ratingType, dataType) %>% mutate( testType = recode( testType, validation = "", test = "" ), groupName = recode( group, elo_all = ", ", elo_off = ", . ", elobeta_all = ", ", elobeta_off = ", . " ), # groupName = factor(groupName, levels = unique(groupName)) ) compute_optimal_k <- . %>% group_by(testType, groupName) %>% slice(which.min(goodness)) %>% ungroup() compute_k_labels <- . %>% compute_optimal_k() %>% mutate(label = paste0("K = ", k)) %>% group_by(groupName) %>% # K , # . - # . mutate(hjust = - (k == max(k)) * 1.1 + 1.05) %>% ungroup() plot_experiment_results <- function(results_tbl) { ggplot(results_tbl) + geom_hline( yintercept = 0.5, colour = "#AA5555", size = 0.5, linetype = "dotted" ) + geom_line(aes(k, goodness, colour = testType)) + geom_vline( data = compute_optimal_k, mapping = aes(xintercept = k, colour = testType), linetype = "dashed", show.legend = FALSE ) + geom_text( data = compute_k_labels, mapping = aes(k, Inf, label = label, hjust = hjust), vjust = 1.2 ) + facet_wrap(~ groupName) + scale_colour_manual( values = c(`` = "#377EB8", `` = "#FF7F00"), guide = guide_legend(title = "", override.aes = list(size = 4)) ) + labs( x = " K", y = " (RMSE)", title = " ", subtitle = paste0( ' ( ) ', ' .\n', ' K ( ', '"") , .' ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_experiment_results(plot_data)
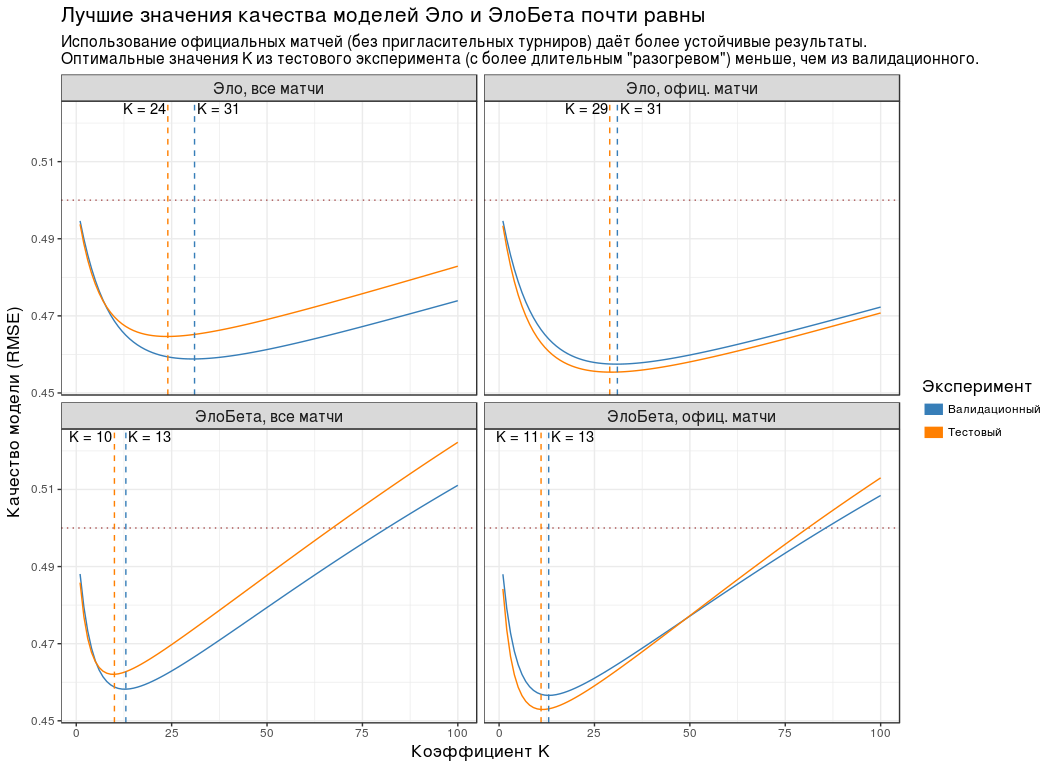
:
- , K , .
- ( "" "" ). , . - "Championship League": 3 .
- RMSE K . , RMSE K "" "". , " " .
- K ( "") , . "", .
- RMSE . 0.5. .
| K | RMSE |
|---|
| , | 24 | 0.465 |
| , . | 29 | 0.455 |
| , | 10 | 0.462 |
| , . | 11 | 0.453 |
क्योंकि , K " " ( ) 5: 30, — 10.
, K=30 K=10 . , एन , .
" " ( K=10 )। - .
-16 2017/18
-16 2017/18 # gather_to_longcr <- function(tbl) { bind_rows( tbl %>% select(-matches("2")) %>% rename_all(funs(gsub("1", "", .))), tbl %>% select(-matches("1")) %>% rename_all(funs(gsub("2", "", .))) ) %>% arrange(game) } # K best_k <- experiment_tbl %>% filter(testType == "test", ratingType == "elobeta", dataType == "off") %>% slice(which.min(goodness)) %>% pull(k) #!!! "" , .. !!! best_k <- round(best_k / 5) * 5 # elobeta_ratings <- rate_iterative( pro_matches_test_off, elobeta_fun_gen(best_k), initial_ratings = 0 ) %>% rename(ratingEloBeta = rating_iterative) %>% arrange(desc(ratingEloBeta)) %>% left_join( y = snooker_players %>% select(id, playerName = name), by = c(player = "id") ) %>% mutate(rankEloBeta = order(ratingEloBeta, decreasing = TRUE)) %>% select(player, playerName, ratingEloBeta, rankEloBeta) elobeta_top16 <- elobeta_ratings %>% filter(rankEloBeta <= 16) %>% mutate( rankChr = formatC(rankEloBeta, width = 2, format = "d", flag = "0"), ratingEloBeta = round(ratingEloBeta, 1) ) official_ratings <- tibble( player = c( 5, 1, 237, 17, 12, 16, 224, 30, 68, 154, 97, 39, 85, 2, 202, 1260 ), rankOff = c( 2, 3, 4, 1, 5, 7, 6, 13, 16, 10, 8, 9, 26, 17, 12, 23 ), ratingOff = c( 905750, 878750, 751525, 1315275, 660250, 543225, 590525, 324587, 303862, 356125, 453875, 416250, 180862, 291025, 332450, 215125 ) )
-16 2017/18 ( snooker.org):
| | | . | . | |
|---|
| Ronnie O'Sullivan | 1 | 128.8 | 2 | 905 750 | 1 |
| Mark J Williams | 2 | 123.4 | 3 | 878 750 | 1 |
| John Higgins | 3 | 112.5 | 4 | 751 525 | 1 |
| Mark Selby | 4 | 102.4 | 1 | 1 315 275 | -3 |
| Judd Trump | 5 | 92.2 | 5 | 660 250 | 0 |
| Barry Hawkins | 6 | 83.1 | 7 | 543 225 | 1 |
| Ding Junhui | 7 | 82.8 | 6 | 590 525 | -1 |
| Stuart Bingham | 8 | 74.3 | 13 | 324 587 | 5 |
| Ryan Day | 9 | 71.9 | 16 | 303 862 | 7 |
| Neil Robertson | 10 | 70.6 | 10 | 356 125 | 0 |
| Shaun Murphy | 11 | 70.1 | 8 | 453 875 | -3 |
| Kyren Wilson | 12 | 70.1 | 9 | 416 250 | -3 |
| Jack Lisowski | 13 | 68.8 | 26 | 180 862 | 13 |
| Stephen Maguire | 14 | 63.7 | 17 | 291 025 | 3 |
| Mark Allen | 15 | 63.7 | 12 | 332 450 | -3 |
| Yan Bingtao | 16 | 61.6 | 23 | 215 125 | 7 |
:
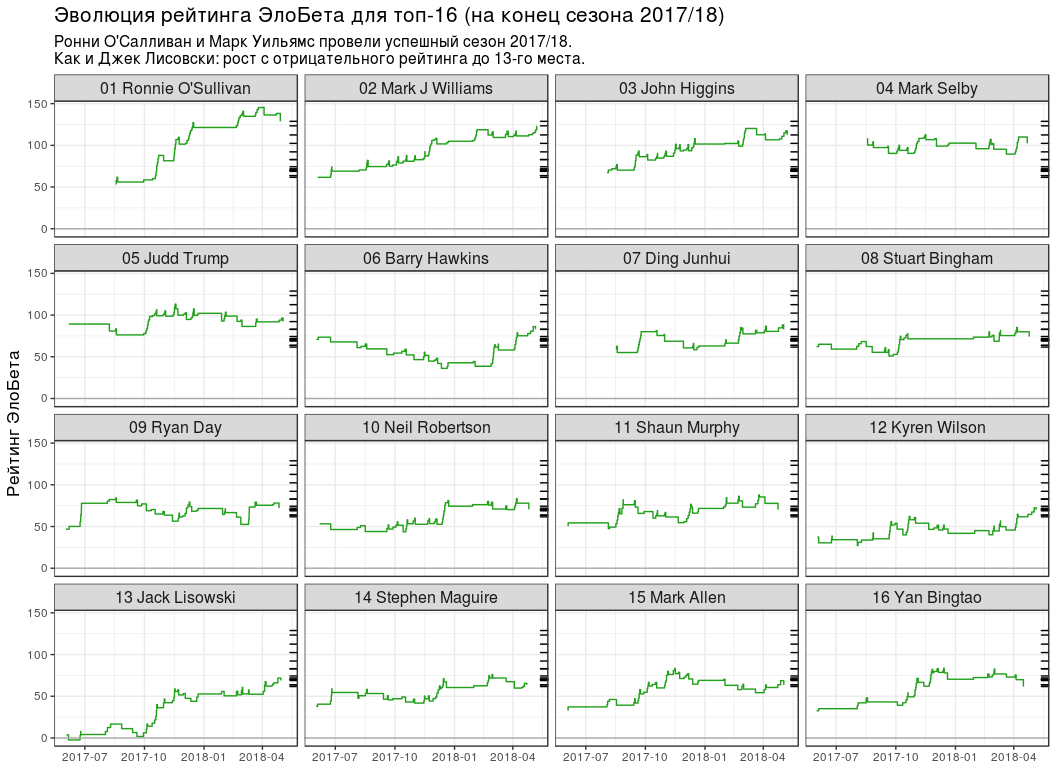
- №1 3 . , , ( ).
- "" ( 13 ), ( 7 ).
- 5 . , 6 - WPBSA. , - "" . : , — .
- .
- ( №11), (№14) (№15) -16. "" (№26), (№23) (№17).
. , №16 (Yan Bingtao) №1 (Ronnie O'Sullivan) 0.404. 4 0.299, " 10 " — 0.197 18 — 0.125. , .
# seasons_break <- ISOdatetime(2017, 5, 2, 0, 0, 0, tz = "UTC") # elobeta_history <- pro_matches_test_off %>% add_iterative_ratings(elobeta_fun_gen(best_k), initial_ratings = 0) %>% gather_to_longcr() %>% left_join(y = pro_matches_test_off %>% select(game, endDate), by = "game") # plot_all_elobeta_history <- function(history_tbl) { history_tbl %>% mutate(isTop16 = player %in% elobeta_top16$player) %>% ggplot(aes(endDate, ratingAfter, group = player)) + geom_step(data = . %>% filter(!isTop16), colour = "#C2DF9A") + geom_step(data = . %>% filter(isTop16), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_vline( xintercept = seasons_break, linetype = "dotted", colour = "#E41A1C", size = 1 ) + geom_text( x = seasons_break, y = Inf, label = " 2016/17", colour = "#E41A1C", hjust = 1.05, vjust = 1.2 ) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = paste0( " -16 2016/17" ), subtitle = paste0( " ", " ." ) ) + theme(title = element_text(size = 13)) } plot_all_elobeta_history(elobeta_history)
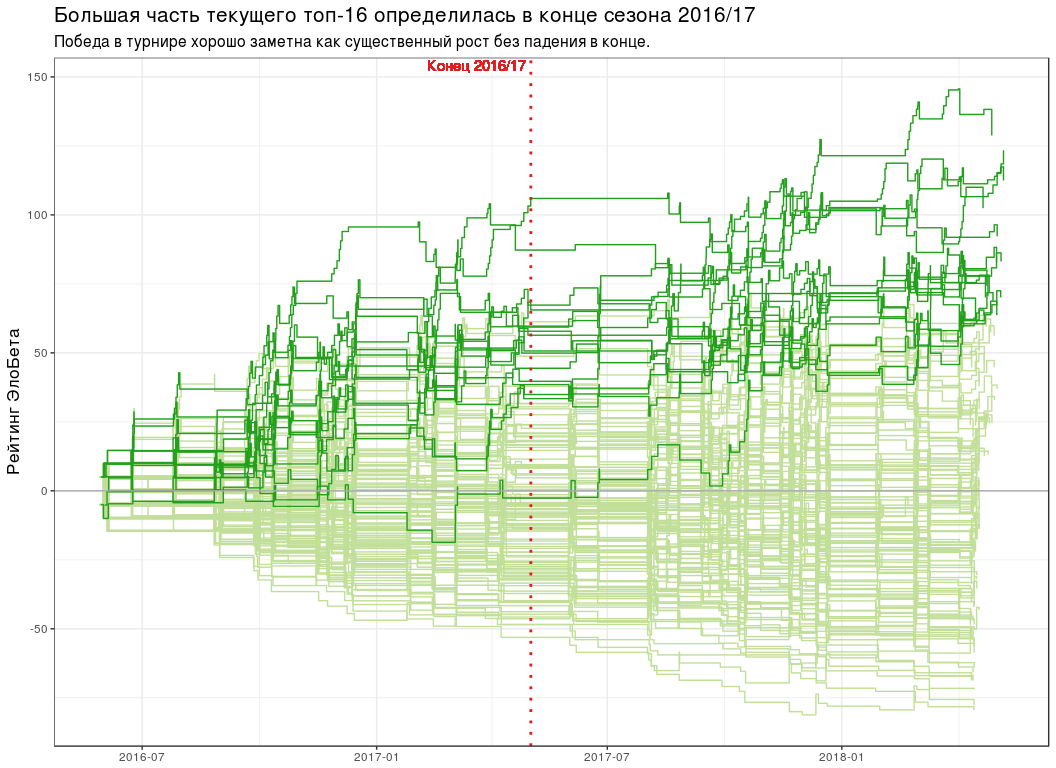
-16
-16 # top16_rating_evolution <- elobeta_history %>% # `inner_join` `elobeta_top16` inner_join(y = elobeta_top16 %>% select(-ratingEloBeta), by = "player") %>% # 2017/18 semi_join( y = pro_matches_test_off %>% filter(season == 2017), by = "game" ) %>% mutate(playerLabel = paste(rankChr, playerName)) # plot_top16_elobeta_history <- function(elobeta_history) { ggplot(elobeta_history) + geom_step(aes(endDate, ratingAfter, group = player), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_rug( data = elobeta_top16, mapping = aes(y = ratingEloBeta), sides = "r" ) + facet_wrap(~ playerLabel, nrow = 4, ncol = 4) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = " -16 ( 2017/18)", subtitle = paste0( " ' 2017/18.\n", " : 13- ." ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_top16_elobeta_history(top16_rating_evolution)
निष्कर्ष
- " " R :
pbeta(p, n, m) . - — "best of एन " ( एन ). .
- K=30 K=10 .
- :
sessionInfo() ## R version 3.4.4 (2018-03-15) ## Platform: x86_64-pc-linux-gnu (64-bit) ## Running under: Ubuntu 16.04.4 LTS ## ## Matrix products: default ## BLAS: /usr/lib/openblas-base/libblas.so.3 ## LAPACK: /usr/lib/libopenblasp-r0.2.18.so ## ## locale: ## [1] LC_CTYPE=ru_UA.UTF-8 LC_NUMERIC=C ## [3] LC_TIME=ru_UA.UTF-8 LC_COLLATE=ru_UA.UTF-8 ## [5] LC_MONETARY=ru_UA.UTF-8 LC_MESSAGES=ru_UA.UTF-8 ## [7] LC_PAPER=ru_UA.UTF-8 LC_NAME=C ## [9] LC_ADDRESS=C LC_TELEPHONE=C ## [11] LC_MEASUREMENT=ru_UA.UTF-8 LC_IDENTIFICATION=C ## ## attached base packages: ## [1] stats graphics grDevices utils datasets methods base ## ## other attached packages: ## [1] bindrcpp_0.2.2 comperank_0.1.0 comperes_0.2.0 ggplot2_2.2.1 ## [5] purrr_0.2.5 tidyr_0.8.1 dplyr_0.7.6 ## ## loaded via a namespace (and not attached): ## [1] Rcpp_0.12.17 knitr_1.20 bindr_0.1.1 magrittr_1.5 ## [5] munsell_0.5.0 tidyselect_0.2.4 colorspace_1.3-2 R6_2.2.2 ## [9] rlang_0.2.1 highr_0.7 plyr_1.8.4 stringr_1.3.1 ## [13] tools_3.4.4 grid_3.4.4 gtable_0.2.0 utf8_1.1.4 ## [17] cli_1.0.0 htmltools_0.3.6 lazyeval_0.2.1 yaml_2.1.19 ## [21] assertthat_0.2.0 rprojroot_1.3-2 digest_0.6.15 tibble_1.4.2 ## [25] crayon_1.3.4 glue_1.2.0 evaluate_0.10.1 rmarkdown_1.10 ## [29] labeling_0.3 stringi_1.2.3 compiler_3.4.4 pillar_1.2.3 ## [33] scales_0.5.0 backports_1.1.2 pkgconfig_2.0.1