जूलिया में KNN कोडिंग और परीक्षण

डाटा साइंस में नई भाषा। जूलिया रूस में एक दुर्लभ भाषा है, हालांकि इसे 5 वर्षों के लिए विदेश में उपयोग किया गया है (उन्होंने मुझे भी आश्चर्यचकित किया)। रूसी में कोई स्रोत नहीं हैं, इसलिए मैंने एक अद्भुत पुस्तक से ली गई जूलिया के बिंदु में एक मामला बनाने का फैसला किया। भाषा सीखने का सबसे अच्छा तरीका है कि आप उसमें कुछ लिखना शुरू करें। और इसके लिए भी ध्यान आकर्षित करने के लिए, मशीन सीखने का उपयोग करें।

नमस्ते हब्रोहितेलम्।

कुछ समय पहले, मैंने जूलिया की नई भाषा सीखना शुरू किया। खैर, नए की तरह। यह मतलूब और अजगर के बीच कुछ है, वाक्यविन्यास बहुत समान है, और भाषा स्वयं C / C ++ में लिखी गई है। सामान्य तौर पर, निर्माण का इतिहास, क्या, क्यों और क्यों विकिपीडिया पर और हैबे पर लेखों के एक जोड़े में है।

पहली चीज जिसने भाषा का मेरा अध्ययन शुरू किया - ठीक है, अंग्रेजी में कौरसेरा गूगल ऑनलाइन पाठ्यक्रम । वहां, मूल वाक्य रचना + के बारे में, अफ्रीका में बीमारियों की भविष्यवाणी पर एक मिनी-प्रोजेक्ट समानांतर में लिखा गया है। मूल बातें और तुरंत अभ्यास। यदि आपको प्रमाणपत्र की आवश्यकता है, तो पूर्ण संस्करण खरीदें। मैं मुफ्त में गया। इस संस्करण के बीच अंतर यह है कि कोई भी आपके परीक्षण और डीजेड की जांच नहीं करेगा। मेरे लिए एक प्रमाण पत्र की तुलना में परिचित होना अधिक महत्वपूर्ण था। (पढ़ें 50 रुपये जाम)

उसके बाद मैंने फैसला किया कि मुझे जूलिया पर एक किताब पढ़नी चाहिए। Google ने पुस्तकों की एक सूची जारी की और समीक्षाओं और समीक्षाओं का अध्ययन करते हुए, उनमें से एक को चुना और अमेज़ॅन पर ऑर्डर किया। पुस्तक संस्करण हमेशा पेंसिल में पढ़ने और आकर्षित करने के लिए अच्छे होते हैं।

जचियास वुल्गैरिस, पीएचडी द्वारा पुस्तक को जूलिया फॉर डेटा साइंस कहा जाता है। मैं जो अंश प्रस्तुत करना चाहता हूं उसमें मेरे द्वारा तय किए गए कोड में कई टाइपो शामिल हैं और इसलिए कार्यशील संस्करण + मेरे परिणाम प्रस्तुत करेंगे।

KNN

यह निकटतम पड़ोसियों की विधि के लिए वर्गीकरण एल्गोरिदम के आवेदन का एक उदाहरण है। संभवतः सबसे पुरानी मशीन लर्निंग एल्गोरिदम में से एक। एल्गोरिथ्म में सीखने का चरण नहीं होता है और यह बहुत तेज़ होता है। इसका अर्थ काफी सरल है: एक नई वस्तु को वर्गीकृत करने के लिए, आपको डेटा सेट (डेटाबेस) से समान "पड़ोसियों" को खोजने की आवश्यकता है और फिर वोट देकर कक्षा का निर्धारण करें।

मैं तुरंत एक आरक्षण कर दूंगा कि जूलिया के पास तैयार किए गए पैकेज हैं, और समय कम करने और त्रुटियों को कम करने के लिए उनका उपयोग करना बेहतर है। लेकिन यह कोड एक तरह से जूलिया सिंटैक्स का संकेत है। किसी फ़ंक्शन के सामान्य रूप के सूखे अर्क को पढ़ने के बजाय उदाहरणों से नई भाषा सीखना मेरे लिए अधिक सुविधाजनक है।

तो, हमारे पास प्रवेश द्वार पर क्या है:

प्रशिक्षण डेटा X (प्रशिक्षण नमूना), प्रशिक्षण डेटा लेबल x (संबंधित लेबल), परीक्षण डेटा Y (परीक्षण चयन), पड़ोसियों की संख्या (पड़ोसियों की संख्या)।

आपको 3 कार्यों की आवश्यकता होगी: दूरी गणना फ़ंक्शन, वर्गीकरण फ़ंक्शन और मुख्य ।

लब्बोलुआब यह है: परीक्षण सरणी के एक तत्व को लें, प्रशिक्षण सरणी के तत्वों से इसकी दूरी की गणना करें। फिर हम उन k तत्वों के सूचकांकों का चयन करते हैं जो जितना संभव हो उतना करीब निकला। हम तत्व को परीक्षण के तहत उस वर्ग में असाइन करते हैं जो कि निकटतम पड़ोसियों के बीच सबसे आम है।

function CalculateDistance{T<:Number}(x::Array{T,1}, y::Array{T,1}) dist = 0 for i in 1:length(x) dist += (x[i] - y[i])^2 end dist = sqrt(dist) return dist end 

एल्गोरिथ्म का मुख्य कार्य। प्रशिक्षण और परीक्षण के नमूने की वस्तुओं के बीच की दूरी का मैट्रिक्स, प्रशिक्षण सेट के लेबल, और निकटतम "पड़ोसियों" की संख्या इनपुट के लिए आती है। आउटपुट नई वस्तुओं और प्रत्येक लेबल की संभावनाओं के लिए अनुमानित लेबल है।

 function Classify{T<:Any}(distances::Array{Float64,1}, labels::Array{T,1}, k::Int) class = unique(labels) nc = length(class) #number of classes indexes = Array(Int,k) #initialize vector of indexes of the nearest neighbors M = typemax(typeof(distances[1])) #the largest possible number that this vector can have class_count = zeros(Int, nc) for i in 1:k indexes[i] = indmin(distances) #returns index of the minimum element in a collection distances[indexes[i]] = M #make sure this element is not selected again end klabels = labels[indexes] for i in 1:nc for j in 1:k if klabels[j] == class[i] class_count[i] +=1 end end end m, index = findmax(class_count) conf = m/k #confidence of prediction return class[index], conf end 

और हां, सभी कार्य।

हमारे पास इनपुट पर प्रशिक्षण सेट X , प्रशिक्षण सेट अंक x , परीक्षण सेट Y और "पड़ोसी" k की संख्या होगी।

आउटपुट पर, हम अनुमानित लेबल और प्रत्येक वर्ग के पुरस्कार की संबंधित संभावनाओं को प्राप्त करेंगे।

 function main{T1<:Number, T2<:Any}(X::Array{T1,2}, x::Array{T2,1}, Y::Array{T1,2}, k::Int) N = size(X,1) n = size(Y,1) D = Array(Float64,N) #initialize distance matrix z = Array(eltype(x),n) #initialize labels vector c = Array(Float64, n) #confidence of prediction for i in 1:n for j in 1:N D[j] = CalculateDistance(X[j,:], vec(Y[i,:])) end z[i], c[i] = Classify(D,x,k) end return z, c end 

एकाधिक साइट परीक्षण

आइए हम क्या मिला परीक्षण करें। सुविधा के लिए, हम फ़ाइल kNN.jl में एल्गोरिथ्म को सहेजते हैं।

आधार को ओपन मशीन लर्निंग कोर्स से उधार लिया गया है। डेटासेट को सैमसंग मानव गतिविधि मान्यता कहा जाता है। डेटा सैमसंग गैलेक्सी एस 3 मोबाइल फोन के एक्सेलेरोमीटर और जायरोस्कोप से आता है, और उसकी जेब में फोन रखने वाले व्यक्ति की गतिविधि का प्रकार भी जाना जाता है - चाहे वह चला गया हो, खड़ा हो, लेटा हो, बैठ गया हो या सीढ़ियों से ऊपर गया हो। हम एक वर्गीकरण समस्या के रूप में शारीरिक गतिविधि के प्रकार को ठीक से निर्धारित करने की समस्या को हल करेंगे।

टैग निम्नलिखित के अनुरूप होगा:
1 - चलना
2 - सीढ़ियों से चढ़ें
3 - सीढ़ियों से नीचे
4 - सीट
5 - इस समय एक व्यक्ति खड़ा था
6 - व्यक्ति झूठ बोल रहा था

 include("kNN.jl") training = readdlm("samsung_train.txt"); training_label = readdlm("samsung_train_labels.txt"); testing = readdlm("samsung_test.txt"); testing_label = readdlm("samsung_test_labels.txt"); training_label = map(Int, training_label) testing_label = map(Int, testing_label) z = main(training, vec(training_label), testing, 7) n = length(testing_label) println(sum(testing_label .== z[1]) / n) 

परिणाम: 0.9053274516457415

संपूर्ण परीक्षण नमूने में सही ढंग से अनुमानित वस्तुओं के अनुपात से गुणवत्ता का आकलन किया जाता है। ऐसा लगता है कि यह इतना बुरा नहीं है। लेकिन मेरा लक्ष्य जूलिया दिखाना है, और यह कि उसके पास डेटा साइंस में जगह है।

दृश्य

अगला, मैं वर्गीकरण परिणामों की कल्पना करने की कोशिश करना चाहता था। ऐसा करने के लिए, आपको दो-आयामी चित्र बनाने की जरूरत है, जिसमें 561 चिन्ह हों और न जाने उनमें से कौन-सा सबसे महत्वपूर्ण हो। इसलिए, सुविधाओं के ऑर्थोगोनल सबस्पेस पर आयामीता और बाद के डेटा डिज़ाइन को कम करने के लिए, प्रधान घटक विश्लेषण (पीसीए) का उपयोग करने का निर्णय लिया गया। जूलिया में, पायथन के रूप में, तैयार किए गए पैकेज हैं, इसलिए हम अपने जीवन को थोड़ा सरल करते हैं।

 using MultivariateStats #for PCA A = testing[1:10,:] #PCA for A M_A = fit(PCA, A'; maxoutdim = 2) Jtr_A = transform(M_A, A'); #PCA for training M = fit(PCA, training'; maxoutdim = 2) Jtr = transform(M, training'); using Gadfly #shows training points and uncertain point pl1 = plot(training, layer(x = Jtr[1,:], y = Jtr[2,:],color = training_label, Geom.point), layer(x = Jtr_A[1,:], y = Jtr_A[2,:], Geom.point)) #predicted values for uncertain points from testing data z1 = main(training, vec(training_label), A, 7) pl2 = plot(training, layer(x = Jtr[1,:], y = Jtr[2,:],color = training_label, Geom.point), layer(x = Jtr_A[1,:], y = Jtr_A[2,:],color = z[1], Geom.point)) vstack(pl1, pl2) 

पहले आंकड़े में, प्रशिक्षण सेट और परीक्षण सेट से कई वस्तुओं को चिह्नित किया जाता है, जिसे उनकी कक्षा को सौंपा जाना चाहिए। तदनुसार, दूसरा आंकड़ा दिखाता है कि इन वस्तुओं को चिह्नित किया गया था।

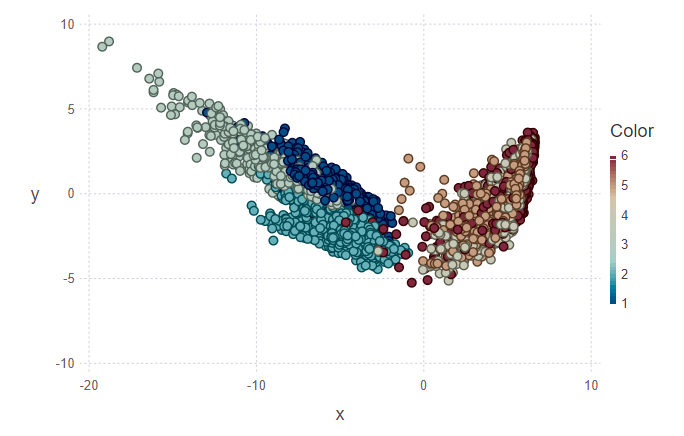
 println(z[1][1:10], z[2][1:10]) > [5, 5, 5, 5, 5, 5, 5, 5, 5, 4][1.0, 0.888889, 0.888889, 0.888889, 1.0, 1.0, 1.0, 1.0, 0.777778, 0.555556] 

छवियों को देखते हुए, मैं सवाल पूछना चाहता हूं "इस तरह के क्लस्टर बदसूरत क्यों हैं?"। मैं समझा दूंगा। डेटा की प्रकृति और पीसीए के उपयोग के कारण व्यक्तिगत क्लस्टर बहुत स्पष्ट रूप से चित्रित नहीं हैं। पीसीए के लिए, बस चलना और सीढ़ियों पर चढ़ना एक वर्ग की तरह है - गति वर्ग। तदनुसार, दूसरा वर्ग बाकी वर्ग है (बैठे, खड़े, झूठ बोलना, जो आपस में बहुत अलग नहीं हैं)। और इसलिए, छह के बजाय दो वर्गों में एक स्पष्ट अलगाव का पता लगाया जा सकता है।

निष्कर्ष

मेरे लिए, यह जूलिया में सिर्फ एक प्रारंभिक विसर्जन है और मशीन सीखने में इस भाषा का उपयोग है। वैसे, जिसमें मैं एक पेशेवर की तुलना में अधिक शौकिया भी हूं। लेकिन जब मुझे दिलचस्पी होगी, मैं इस मामले का और गहराई से अध्ययन करना जारी रखूंगा। कई विदेशी स्रोतों ने जूलिया पर दांव लगाया। खैर, इंतजार कीजिए और देखिए।

पुनश्च: यदि यह दिलचस्प है, तो मैं आपको निम्नलिखित पोस्टों में सिंटैक्स की सुविधाओं के बारे में, आईडीई के बारे में बता सकता हूं, जिनकी स्थापना के साथ मुझे समस्याएं थीं।