🧑🏾‍🤝‍🧑🏼 👨🏼‍⚕️ 🏴󠁧󠁢󠁷󠁬󠁳󠁿 विभेदक समीकरणों की प्रणालियों द्वारा दी गई वस्तुओं के गणितीय मॉडल का संख्यात्मक समाधान 🧗🏿 🧘🏼 👨🏿‍🍳

परिचय:

कई तकनीकी उपकरणों के गणितीय मॉडलिंग में, अंतर nonlinear समीकरणों के सिस्टम का उपयोग किया जाता है। इस तरह के मॉडल न केवल प्रौद्योगिकी में उपयोग किए जाते हैं, उनका उपयोग अर्थशास्त्र, रसायन विज्ञान, जीव विज्ञान, चिकित्सा और प्रबंधन में किया जाता है।

ऐसे उपकरणों के कामकाज के अध्ययन के लिए समीकरणों के इन प्रणालियों के समाधान की आवश्यकता होती है। चूंकि इस तरह के समीकरणों के थोक गैर-स्थिर और गैर-स्थिर होते हैं, इसलिए उनका विश्लेषणात्मक समाधान प्राप्त करना अक्सर असंभव होता है।

संख्यात्मक विधियों का उपयोग करने की आवश्यकता है, जिनमें से सबसे प्रसिद्ध रन-कुट्टा विधि है [1]। जैसा कि पायथन के लिए, संख्यात्मक विधियों पर प्रकाशनों में, उदाहरण के लिए [2,3], रनगे - कुट्टा के उपयोग पर बहुत कम डेटा है, और रनगे - कुट्टा - फेलबर्ग विधि के इसके संशोधन पर कोई डेटा नहीं है।

वर्तमान में, अपने सरल इंटरफ़ेस के लिए, scipy.integrate मॉड्यूल से odeint फ़ंक्शन का पायथन में सबसे बड़ा वितरण है। इस मॉड्यूल से दूसरा फ़ंक्शन कई तरीकों को लागू करता है, जिसमें उल्लेखित पांच-रैंक रनगे-कुट्टा-फेलबर्ग विधि शामिल है, लेकिन, इसकी सार्वभौमिकता के कारण, सीमित प्रदर्शन है।

इस प्रकाशन का उद्देश्य पायजॉन के तहत एक संशोधित लेखक के साथ रन-कुट्टा-फेलबर्ग विधि के साथ अंतर समीकरणों के संख्यात्मक रूप से हल करने की प्रणाली के लिए सूचीबद्ध साधनों का तुलनात्मक विश्लेषण है। प्रकाशन विभेदक समीकरणों (एसडीई) की प्रणालियों के लिए सीमा मूल्य की समस्याओं का समाधान भी प्रदान करता है।

सीडीएस के संख्यात्मक समाधान के लिए विचार किए गए तरीकों और सॉफ्टवेयर पर संक्षिप्त सैद्धांतिक और वास्तविक डेटा

कैची की समस्या

Nth आदेश के एक अंतर समीकरण के लिए, कॉची समस्या समानता को संतुष्ट करने वाले एक फ़ंक्शन को खोजने में शामिल है:

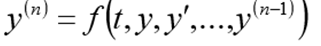
और प्रारंभिक शर्तें

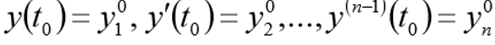
इस समस्या को हल करने से पहले निम्नलिखित सीडीएस के रूप में फिर से लिखा जाना चाहिए

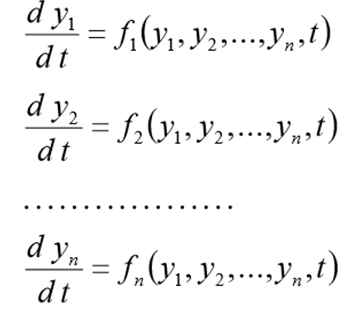
(1)

प्रारंभिक स्थितियों के साथ

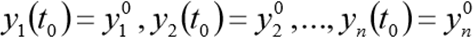Scipy.integrate मॉड्यूल

मॉड्यूल में दो कार्य ode () और odeint () हैं, जिन्हें पहले क्रम के साधारण अंतर समीकरणों (ODEs) के सिस्टम को एक बिंदु (काऊची समस्या) पर प्रारंभिक स्थितियों के साथ हल करने के लिए डिज़ाइन किया गया है। Ode () फ़ंक्शन अधिक सार्वभौमिक है, और odeint () (ODE इंटीग्रेटर) फ़ंक्शन का एक सरल इंटरफ़ेस है और अधिकांश समस्याओं को अच्छी तरह हल करता है।

ओडिन्ट () फ़ंक्शन

Odeint () फ़ंक्शन में तीन आवश्यक तर्क और कई विकल्प हैं। इसके निम्न स्वरूप हैं odeint (func, y0, t [, args = (..., ...)) तर्क दुर्गंध दो चर के कार्य का पायथन नाम है, जिनमें से पहली सूची y = [y1, y2, ..., yn है ], और दूसरा स्वतंत्र चर का नाम है।

फंक फ़ंक्शन को एन फ़ंक्शन मानों की सूची वापस करनी चाहिए

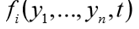
स्वतंत्र तर्क टी के दिए गए मूल्य के लिए। वास्तव में, फंक (y, t) फ़ंक्शन सिस्टम के दाहिने-हाथ के पक्षों की गणना को लागू करता है (1)।

Odeint () का दूसरा तर्क y0 प्रारंभिक मानों का एक सरणी (या सूची) है

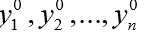
t = t0 पर।

तीसरा तर्क समय बिंदुओं का एक सरणी है जिस पर आप समस्या का समाधान प्राप्त करना चाहते हैं। इस स्थिति में, इस सरणी का पहला तत्व t0 माना जाता है।

Odeint () फ़ंक्शन आकार len (t) x len (y0) की एक सरणी देता है। Odeint () फ़ंक्शन में कई विकल्प हैं जो इसके संचालन को नियंत्रित करते हैं। Rtol (सापेक्ष त्रुटि) और एटोल (पूर्ण त्रुटि) विकल्प सूत्र के अनुसार yi के प्रत्येक मान के लिए गणना त्रुटि ei निर्धारित करते हैं।

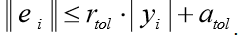
वे वैक्टर या स्केलर हो सकते हैं। डिफ़ॉल्ट रूप से

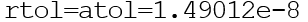ऑड () फ़ंक्शन

Scipy.integrate मॉड्यूल का दूसरा फ़ंक्शन, जिसे अंतर समीकरणों और प्रणालियों को हल करने के लिए डिज़ाइन किया गया है, को ode () कहा जाता है। यह एक ODE ऑब्जेक्ट बनाता है (प्रकार scipy.integrate._ode.ode)। इस तरह के ऑब्जेक्ट का लिंक होने पर, किसी को अंतर समीकरणों को हल करने के लिए अपने तरीकों का उपयोग करना चाहिए। इसी तरह odeint () फ़ंक्शन के लिए, ode (func) फ़ंक्शन में फॉर्म (1) के अंतर समीकरणों की एक प्रणाली की समस्या को कम करना और दाएं हाथ के पक्षों के अपने फ़ंक्शन का उपयोग करना शामिल है।

एकमात्र अंतर यह है कि दाहिने हाथ के फंक (t, y) का कार्य एक स्वतंत्र चर को पहले तर्क के रूप में स्वीकार करता है, और दूसरे के रूप में वांछित कार्यों के मूल्यों की सूची। उदाहरण के लिए, निर्देशों का निम्न अनुक्रम एक ODE बनाता है जो एक कॉची कार्य का प्रतिनिधित्व करता है।

रनगति - कुट्टा विधि

संख्यात्मक एल्गोरिदम का निर्माण करते समय, हम मानते हैं कि इस अंतर समस्या का समाधान मौजूद है, यह अद्वितीय है और इसमें आवश्यक चिकनाई गुण हैं।

कैची समस्या के संख्यात्मक समाधान में

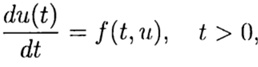
(2)

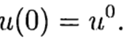
(3)

बिंदु t = 0 पर ज्ञात समाधान के अनुसार, अन्य t के लिए समीकरण (3) से हल खोजना आवश्यक है। समस्या के संख्यात्मक समाधान में (2), (3), हम एक समान का उपयोग करेंगे, सादगी के लिए, चरण टी> 0 के साथ चर टी में ग्रिड।

समस्या का एक अनुमानित समाधान (2), (3) बिंदु पर

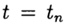
लक्षित

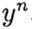
। विधि एक बिंदु पर परिवर्तित होती है

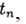
अगर

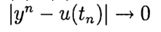
पर

। विधि सटीकता का एक pth क्रम है अगर

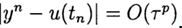
, p> 0 के लिए

। समस्या के लगभग समाधान के लिए सबसे सरल अंतर योजना (2), (3) है

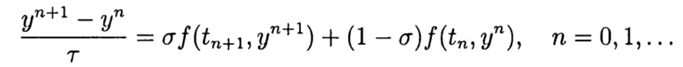
(4)

पर

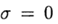
हमारे पास एक स्पष्ट विधि है और इस मामले में अंतर योजना पहले आदेश के साथ समीकरण (2) का अनुमान लगाती है। सममित डिजाइन

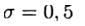
(4) में सन्निकटन का दूसरा क्रम है। यह योजना निहित वर्ग से संबंधित है - एक नई परत पर अनुमानित समाधान का निर्धारण करने के लिए, गैर-समस्या को हल करना आवश्यक है।

भविष्यवक्ता-सुधारक विधि के आधार पर स्पष्ट दूसरी और उच्च-क्रम सन्निकटन योजनाओं का निर्माण करना सुविधाजनक है। भविष्यवक्ता (भविष्यवाणी) के स्तर पर, एक स्पष्ट योजना का उपयोग किया जाता है।

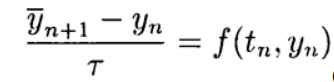
(5)

और सुधारक (परिशोधन) स्तर पर, एक आरेख

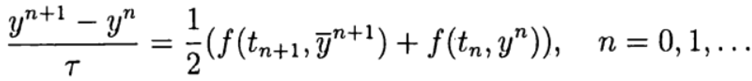
एक-चरण रूज - कुट्टा विधियों में, भविष्यवक्ता-सुधारक के विचारों को पूरी तरह से महसूस किया जाता है। यह विधि सामान्य रूप में लिखी गई है:

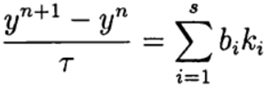
(6)

जहाँ

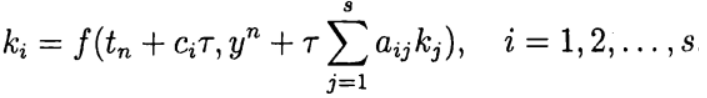
फॉर्मूला (6) फ़ंक्शन च की गणना पर आधारित है और इसे एस-स्टेज कहा जाता है। अगर

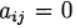
पर

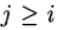
हमारे पास स्पष्ट रूज - कुट्टा विधि है। अगर

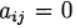
j> 1 और के लिए

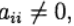
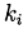
समीकरण से स्पष्ट रूप से निर्धारित:

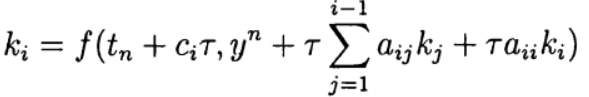
(7)

यह रनग - कुट्टा विधि को तिरछे निहित के रूप में कहा जाता है। मापदंडों

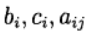
रूज - कुट्टा विधि का एक प्रकार निर्धारित करें। विधि का निम्नलिखित प्रतिनिधित्व प्रयोग किया जाता है (बुचर टेबल)

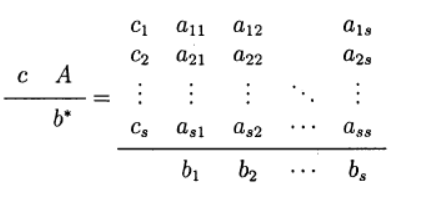
सबसे आम में से एक चौथा क्रम स्पष्ट रूज है - कुट्टा विधि।

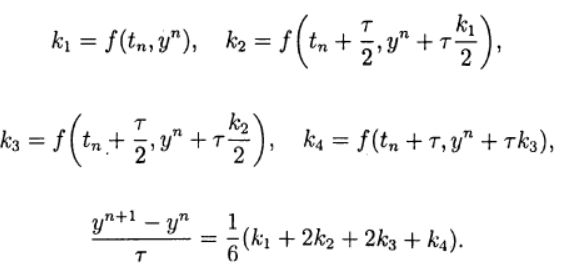
(8)

रनगे - कुट्टा - फेलबर्ग विधि

मैं गणना किए गए गुणांक का मूल्य देता हूं

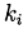
विधि

(9)

(9) के मद्देनजर, सामान्य समाधान के रूप हैं:

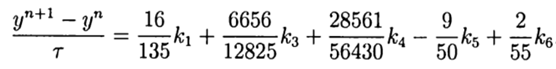
(10)

यह समाधान सटीकता का पांचवा क्रम प्रदान करता है, यह इसे पायथन के अनुकूल बनाने के लिए रहता है।

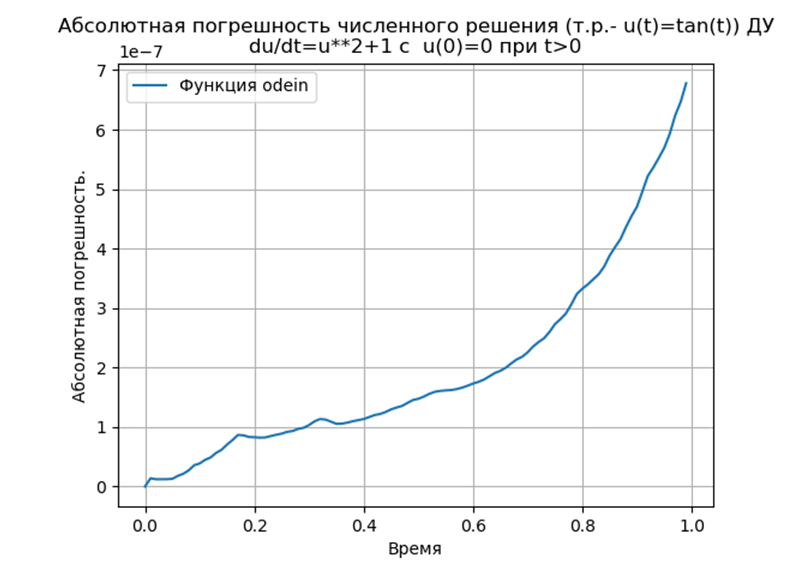
एक nonlinear अंतर समीकरण के संख्यात्मक समाधान की पूर्ण त्रुटि निर्धारित करने के लिए कम्प्यूटेशनल प्रयोग 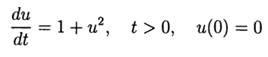दोनों कार्यों का उपयोग करते हुए odein (), def oden () of scipy.integrate मॉड्यूल और रन-कुट्टा और रन-कुट्टा - फेलबर्ग विधियों को पायथन के लिए अनुकूलित किया गया

कार्यक्रम सूचीकरण

from numpy import* import matplotlib.pyplot as plt from scipy.integrate import * def odein(): #dy1/dt=y2 #dy2/dt=y1**2+1: def f(y,t): return y**2+1 t =arange(0,1,0.01) y0 =0.0 y=odeint(f, y0,t) y = array(y).flatten() return y,t def oden(): f = lambda t, y: y**2+1 ODE=ode(f) ODE.set_integrator('dopri5') ODE.set_initial_value(0, 0) t=arange(0,1,0.01) z=[] t=arange(0,1,0.01) for i in arange(0,1,0.01): ODE.integrate(i) q=ODE.y z.append(q[0]) return z,t def rungeKutta(f, to, yo, tEnd, tau): def increment(f, t, y, tau): if z==1: k0 =tau* f(t,y) k1 =tau* f(t+tau/2.,y+k0/2.) k2 =tau* f(t+tau/2.,y+k1/2.) k3 =tau* f(t+tau, y + k2) return (k0 + 2.*k1 + 2.*k2 + k3) / 6. elif z==0: k1=tau*f(t,y) k2=tau*f(t+(1/4)*tau,y+(1/4)*k1) k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2) k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3) k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4) k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5) return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6 t = [] y= [] t.append(to) y.append(yo) while to < tEnd: tau = min(tau, tEnd - to) yo = yo + increment(f, to, yo, tau) to = to + tau t.append(to) y.append(yo) return array(t), array(y) def f(t, y): f = zeros([1]) f[0] = y[0]**2+1 return f to = 0. tEnd = 1 yo = array([0.]) tau = 0.01 z=1 t, yn = rungeKutta(f, to, yo, tEnd, tau) y1n=[i[0] for i in yn] plt.figure() plt.title("   (..- u(t)=tan(t)) \n\ du/dt=u**2+1 cu(0)=0  t>0") plt.plot(t,abs(array(y1n)-array(tan(t))),label=' — \n\   -   ') plt.xlabel('') plt.ylabel(' .') plt.legend(loc='best') plt.grid(True) z=0 t, ym = rungeKutta(f, to, yo, tEnd, tau) y1m=[i[0] for i in ym] plt.figure() plt.title("   (..- u(t)=tan(t)) \n\ du/dt=u**2+1 cu(0)=0  t>0") plt.plot(t,abs(array(y1m)-array(tan(t))),label=' ——  \n\   -   ') plt.xlabel('') plt.ylabel(' .') plt.legend(loc='best') plt.grid(True) plt.figure() plt.title("    (..- u(t)=tan(t)) \n\ du/dt=u**2+1 cu(0)=0  t>0") y,t=odein() plt.plot(t,abs(array(tan(t))-array(y)),label=' odein') plt.xlabel('') plt.ylabel(' .') plt.legend(loc='best') plt.grid(True) plt.figure() plt.title("    (..- u(t)=tan(t)) \n\ du/dt=u**2+1 cu(0)=0  t>0") z,t=oden() plt.plot(t,abs(tan(t)-z),label=' ode  ——  \n\  ') plt.xlabel('') plt.ylabel(' .') plt.legend(loc='best') plt.grid(True) plt.show()

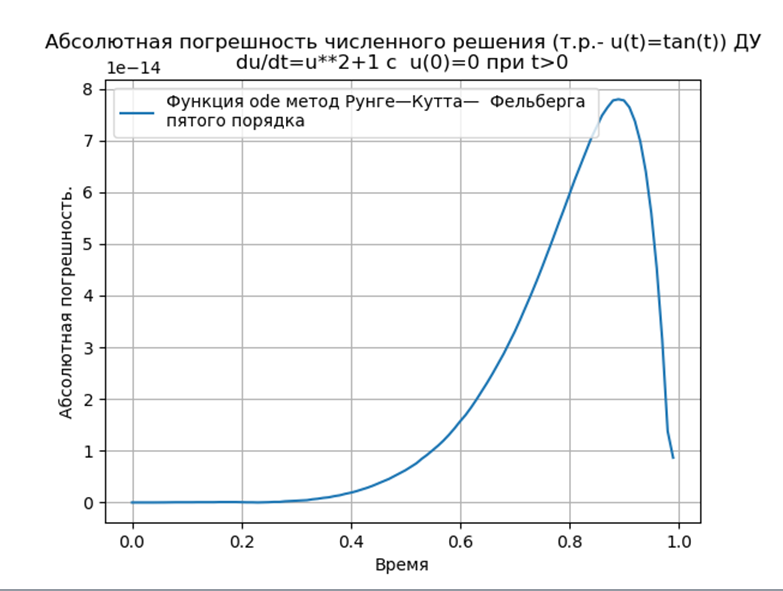
हमें मिलता है:

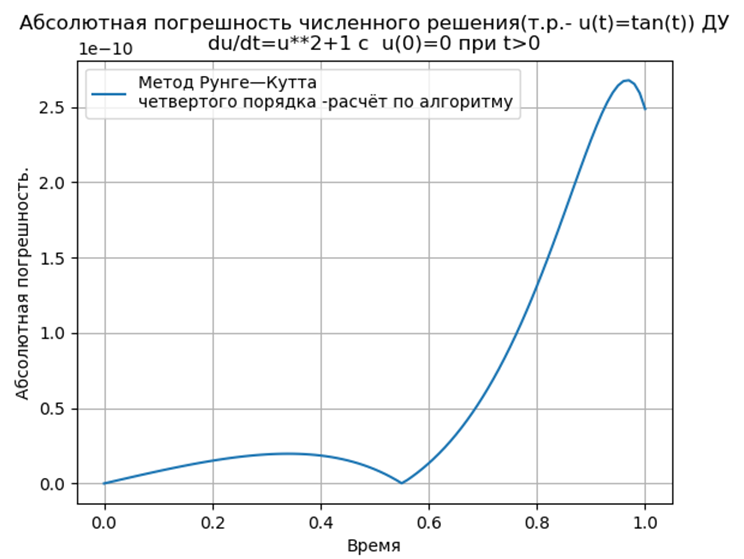
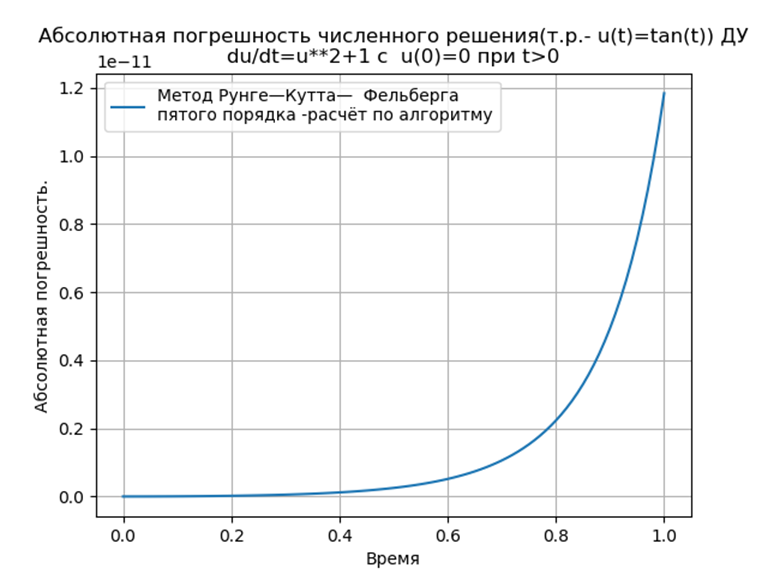
निष्कर्ष:

पायथन-रूपांतरित रूज - कुट्टा और रंज - कुट्टा - फेलबर्ग विधियों में odeint फ़ंक्शन का उपयोग करके समाधान की तुलना में कम निरपेक्ष है, लेकिन edu फ़ंक्शन का उपयोग करके समाधान से अधिक है। एक प्रदर्शन अध्ययन करना आवश्यक है।

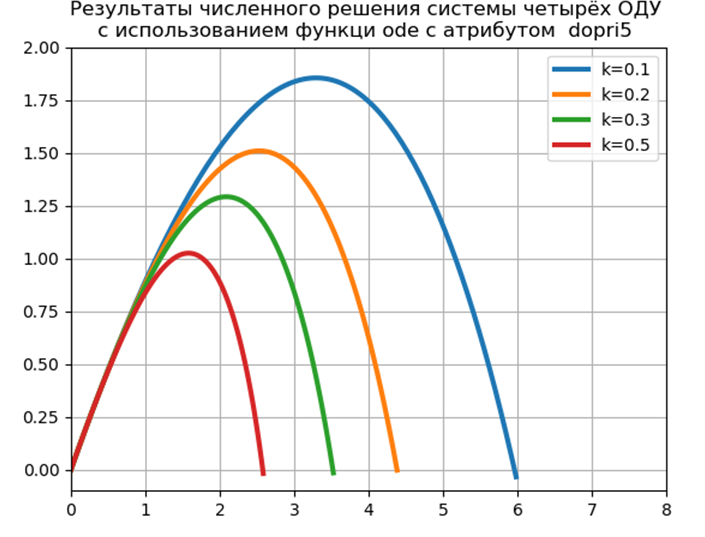
एक संख्यात्मक प्रयोग, डोप्री 5 विशेषता (रन - कुट्टा विधि 5 वें क्रम की विधि) के साथ ओडे फ़ंक्शन का उपयोग करके एसडीई के संख्यात्मक समाधान की गति की तुलना करते हुए और रनगे - कुट्टा - फेलबर्ग ने पायथन के लिए अनुकूलित किया।

एक उदाहरण के रूप में [2] में दी गई मॉडल समस्या का उपयोग करके एक तुलनात्मक विश्लेषण किया जाता है। स्रोत को नहीं दोहराने के लिए, मैं मॉडल समस्या का सूत्रीकरण और समाधान [2] से प्रस्तुत करूंगा।

आइए हम कैची समस्या का समाधान करते हैं, जो इस अनुमान के तहत एक कोण α पर एक प्रारंभिक वेग v0 के साथ फेंके गए शरीर की गति का वर्णन करती है, इस धारणा के तहत कि वायु प्रतिरोध वेग के वर्ग के लिए आनुपातिक है। सदिश रूप में, गति के समीकरण का रूप है

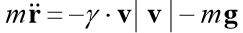
जहाँ

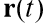
गतिमान शरीर के वेक्टर की त्रिज्या है,

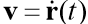
शरीर का वेग वेक्टर है,

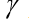
- गुणांक, वेक्टर खींचें

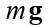
द्रव्यमान m के भार के बल, g - गुरुत्वाकर्षण का त्वरण।

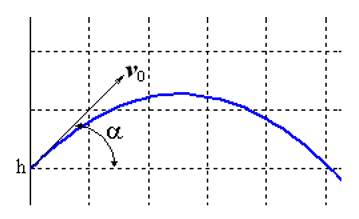
इस कार्य की ख़ासियत यह है कि यह आंदोलन पहले अज्ञात समय पर समाप्त होता है जब शरीर जमीन पर गिर जाता है। यदि नामित हो

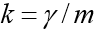
, तो समन्वय रूप में हमारे पास समीकरणों की एक प्रणाली है:

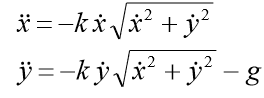
प्रारंभिक शर्तों को सिस्टम में जोड़ा जाना चाहिए:

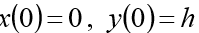
(एच प्रारंभिक ऊंचाई)

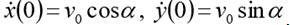
। रखना

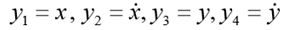
। तब संबंधित प्रथम-क्रम ODE सिस्टम फॉर्म लेता है:

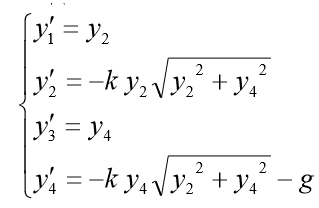
मॉडल समस्या के लिए हम डालते हैं

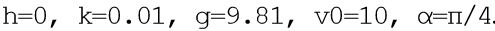
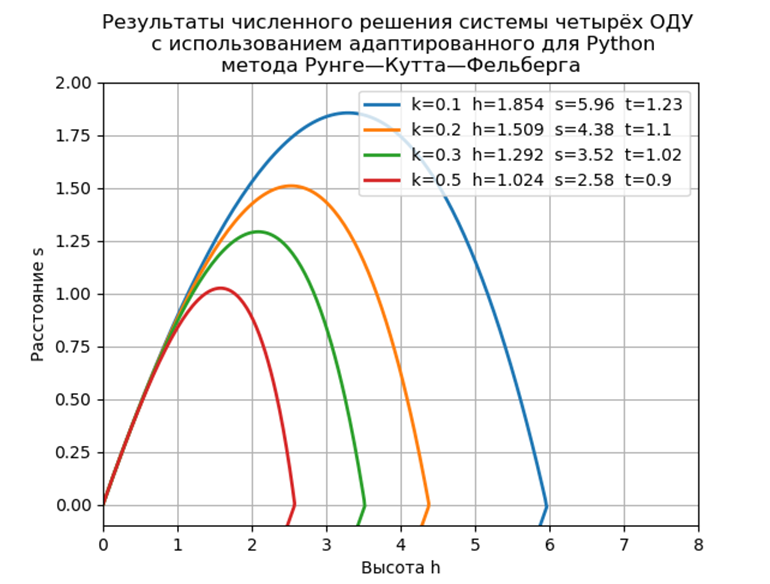
। कार्यक्रम के एक विस्तृत विवरण को स्वीकार करते हुए, मैं केवल टिप्पणियों से एक सूची दूंगा, जो मुझे लगता है कि, इसके संचालन का सिद्धांत स्पष्ट होगा। कार्यक्रम ने तुलनात्मक विश्लेषण के लिए एक उलटी गिनती जोड़ दी है।

कार्यक्रम सूचीकरण

 import numpy as np import matplotlib.pyplot as plt import time start = time.time() from scipy.integrate import ode ts = [ ] ys = [ ] FlightTime, Distance, Height =0,0,0 y4old=0 def fout(t, y):#   global FlightTime, Distance, Height,y4old ts.append(t) ys.append(list(y.copy())) y1, y2, y3, y4 = y if y4*y4old<=0: #    Height=y3 if y4<0 and y3<=0.0: #    FlightTime=t Distance=y1 return -1 y4old=y4 #      def f(t, y, k): #    k g=9.81 y1, y2, y3, y4 = y return [y2,-k*y2*np.sqrt(y2**2+y4**2), y4,-k*y4*np.sqrt(y2**2+y4**2)-g] tmax=1.41 #     alph=np.pi/4 #    v0=10.0 #   K=[0.1,0.2,0.3,0.5] #    y0,t0=[0, v0*np.cos(alph), 0, v0*np.sin(alph)], 0 #   ODE=ode(f) ODE.set_integrator('dopri5', max_step=0.01) ODE.set_solout(fout) fig, ax = plt.subplots() fig.set_facecolor('white') for k in K: #     ts, ys = [ ],[ ] ODE.set_initial_value(y0, t0) #    ODE.set_f_params(k) #    k #   f(t,y,k)     ODE.integrate(tmax) #   print('Flight time = %.4f Distance = %.4f Height =%.4f '% (FlightTime,Distance,Height)) Y=np.array(ys) plt.plot(Y[:,0],Y[:,2],linewidth=3,label='k=%.1f'% k) stop = time.time() plt.title("      \n    ode   dopri5 ") print ("   : %f"%(stop-start)) plt.grid(True) plt.xlim(0,8) plt.ylim(-0.1,2) plt.legend(loc='best') plt.show()

हमें मिलता है:

उड़ान का समय = 1.2316 दूरी = 5.9829 ऊँचाई = 1.8542
उड़ान का समय = 1.1016 दूरी = 4.3830 ऊँचाई = 1.5088
उड़ान का समय = 1.0197 दूरी = 3.5265 ऊँचाई = 1.2912
उड़ान का समय = 0.9068 दूरी = 2.5842 ऊँचाई = 1.0240
मॉडल समस्या के लिए समय: 0.454787

विशेष मॉड्यूल का उपयोग किए बिना पायथन टूल्स का उपयोग करते हुए सीडीएस के संख्यात्मक समाधान को लागू करने के लिए, मैंने निम्न फ़ंक्शन का प्रस्ताव और जांच की:

def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6

वृद्धि (f, t, y, tau) फ़ंक्शन संख्यात्मक समाधान विधि का पांचवा क्रम प्रदान करता है। कार्यक्रम की अन्य विशेषताएं निम्नलिखित सूची में पाई जा सकती हैं:

कार्यक्रम सूचीकरण

 from numpy import* import matplotlib.pyplot as plt import time start = time.time() def rungeKutta(f, to, yo, tEnd, tau): def increment(f, t, y, tau):#     ——. k1=tau*f(t,y) k2=tau*f(t+(1/4)*tau,y+(1/4)*k1) k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2) k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3) k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4) k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5) return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6 t = []#   t y= []#   y t.append(to)#   t   to y.append(yo)#   y   yo while to < tEnd:#     t,y tau = min(tau, tEnd - to)#   tau yo = yo + increment(f, to, yo, tau) #     t0,y0    to = to + tau #   t.append(to) #   t y.append(yo) #   y return array(t), array(y) def f(t, y): #      f = zeros([4]) f[0]=y[1] f[1]=-k*y[1]*sqrt(y[1]**2+y[3]**2) f[2]=y[3] f[3]=-k*y[3]*sqrt(y[1]**2+y[3]**2) -g if y[3]<0 and y[2]<=0.0: #    return -1 return f to = 0#     tEnd = 1.41#     alph=pi/4#    v0=10.0 #   K=[0.1,0.2,0.3,0.5]#     g=9.81 yo = array([0.,v0*cos(alph),0.,v0*sin(alph)]) #   tau =0.01#  for i in K: #      k=i t, y = rungeKutta(f, to, yo, tEnd, tau) y1=array([i[0] for i in y]) #     y y3=array([i[2] for i in y]) #    ""     s,h,t plt.plot(y1,y3,linewidth=2,label='k=%.1f h=%.3f s=%.2f t=%s' % (k,max(y3),max(y1),round(t[list(y1).index(max(y1))],3))) stop = time.time() plt.title("      \n     Python\n  —— ") print ("   : %f"%(stop-start)) plt.xlabel(' h') plt.ylabel(' s') plt.legend(loc='best') plt.xlim(0,8) plt.ylim(-0.1,2) plt.grid(True) plt.show()

हमें मिलता है:

मॉडल समस्या के लिए समय: 0.259927

निष्कर्ष

विशेष मॉड्यूल के उपयोग के बिना मॉडल की समस्या के प्रस्तावित सॉफ्टवेयर कार्यान्वयन में ode फ़ंक्शन की तुलना में लगभग दो गुना तेज प्रदर्शन होता है, लेकिन हमें यह नहीं भूलना चाहिए कि ode में संख्यात्मक समाधान की उच्च सटीकता और समाधान विधि चुनने की संभावना है।

थ्रेड-अलग सीमा स्थितियों के साथ एक सीमा मूल्य समस्या का समाधान

हम थ्रेड-अलग सीमा स्थितियों के साथ एक विशिष्ट सीमा-मूल्य समस्या का एक उदाहरण देते हैं:

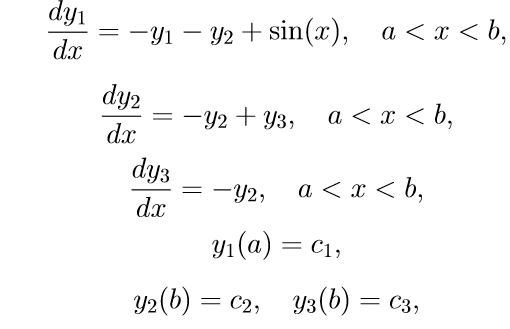
(11)

समस्या को हल करने के लिए (11), हम निम्नलिखित एल्गोरिथ्म का उपयोग करते हैं:

1. हम प्रारंभिक स्थितियों के साथ सिस्टम के पहले तीन अमानवीय समीकरणों (11) को हल करते हैं

हम Cauchy समस्या को हल करने के लिए संकेतन प्रस्तुत करते हैं:

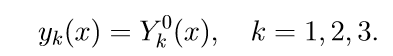
2. हम प्रारंभिक स्थितियों के साथ सिस्टम (11) के पहले तीन सजातीय समीकरण हल करते हैं

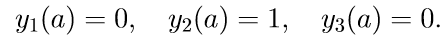
हम Cauchy समस्या को हल करने के लिए संकेतन प्रस्तुत करते हैं:

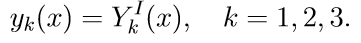
3. हम प्रारंभिक स्थितियों के साथ सिस्टम के पहले तीन सजातीय समीकरण (11) को हल करते हैं

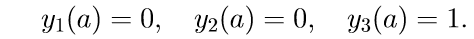
हम Cauchy समस्या को हल करने के लिए संकेतन प्रस्तुत करते हैं:

4. कॉची समस्याओं के समाधान का उपयोग करते हुए सीमा मूल्य समस्या (11) का सामान्य समाधान समाधानों के रैखिक संयोजन के रूप में लिखा गया है:

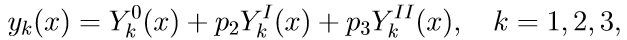
जहां पी 2, पी 3 कुछ अज्ञात पैरामीटर हैं।

5. मापदंडों को निर्धारित करने के लिए पी 2, पी 3, हम पिछले दो समीकरणों (11) की सीमा स्थितियों का उपयोग करते हैं, अर्थात, एक्स = बी के लिए शर्तें। प्रतिस्थापन, हम अज्ञात P2, p3 के संबंध में रैखिक समीकरणों की एक प्रणाली प्राप्त करते हैं:

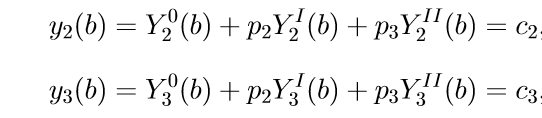
(12)
समाधान (12), हम पी 2, पी 3 के लिए संबंध प्राप्त करते हैं।

उपर्युक्त एल्गोरिथ्म का उपयोग रन-कुट्टा - फेलबर्ग विधि का उपयोग करके, हम निम्नलिखित कार्यक्रम प्राप्त करते हैं:

कार्यक्रम सूचीकरण

  #   from numpy import* import matplotlib.pyplot as plt import matplotlib.font_manager as fm,os import matplotlib.patches as mpatches import matplotlib.lines as mlines from scipy.integrate import odeint from scipy import linalg import time start = time.time() c1 = 1.0 c2 = 0.8 c3 = 0.5 a =0.0 b = 1.0 nn =100 initial_state_0 =array( [a, c1, 0.0, 0.0]) initial_state_I =array( [a, 0.0, 1.0, 0.0]) initial_state_II =array( [a, 0.0, 0.0, 1.0]) to = a tEnd =b N = int(nn) tau=(ba)/N def rungeKutta(f, to, yo, tEnd, tau): def increment(f, t, y, tau): k1=tau*f(t,y) k2=tau*f(t+(1/4)*tau,y+(1/4)*k1) k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2) k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3) k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4) k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5) return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6 t = [] y= [] t.append(to) y.append(yo) while to < tEnd: tau = min(tau, tEnd - to) yo = yo + increment(f, to, yo, tau) to = to + tau t.append(to) y.append(yo) return array(t), array(y) def f(t, y): global theta f = zeros([4]) f[0] = 1 f[1] = -y [1]-y[2] +theta* sin(y[0]) f[2] = -y[2]+y[3] f[3] = -y[2] return f #    -- theta = 1 theta = 1.0 yo =initial_state_0 t, y = rungeKutta(f, to, yo, tEnd, tau) y2=[i[2] for i in y] y3=[i[3] for i in y] #       # Y20 = Y2(b), Y30 = Y3(b) Y20 = y2[N-1] Y30 = y3[N-1] #    -- theta = 0,  I theta = 0.0 yo= initial_state_I t, y = rungeKutta(f, to, yo, tEnd, tau) y2=[i[2] for i in y] y3=[i[3] for i in y] #       # Y21= Y2(b), Y31 = Y3(b) Y21= y2[N-1] Y31 = y3[N-1] #    -- theta = 0,  II theta = 0.0 yo =initial_state_II t, y = rungeKutta(f, to, yo, tEnd, tau) y2=[i[2] for i in y] y3=[i[3] for i in y] #       # Y211= Y2(b), Y311 = Y3(b) Y211= y2[N-1] Y311 = y3[N-1] #    #     p2, p3 b1 = c2 - Y20 b2 = c3 - Y30 A = array([[Y21, Y211], [Y31, Y311]]) bb = array([[b1], [b2]]) #   p2, p3 = linalg.solve(A, bb) #    #  , theta = 1 theta = 1.0 yo = array([a, c1, p2, p3]) t, y = rungeKutta(f, to, yo, tEnd, tau) y0=[i[0] for i in y] y1=[i[1] for i in y] y2=[i[2] for i in y] y3=[i[3] for i in y] #  print('y0[0]=', y0[0]) print('y1[0]=', y1[0]) print('y2[0]=', y2[0]) print('y3[0]=', y3[0]) print('y0[N-1]=', y0[N-1]) print('y1[N-1]=', y1[N-1]) print('y2[N-1]=', y2[N-1]) print('y3[N-1]=', y3[N-1]) j = N xx = y0[:j] yy1 = y1[:j] yy2 = y2[:j] yy3 = y3[:j] stop = time.time() print ("   : %f"%(stop-start)) plt.subplot(2, 1, 1) plt.plot([a], [c1], 'ro') plt.plot([b], [c2], 'go') plt.plot([b], [c3], 'bo') plt.plot(xx, yy1, color='r') #  plt.plot(xx, yy2, color='g') #  plt.plot(xx, yy3, color='b') #  plt.xlabel(r'$x$') #   x   TeX plt.ylabel(r'$y_k(x)$') #   y   TeX plt.title(r'  ', color='blue') plt.grid(True) # patch_y1 = mpatches.Patch(color='red', label='$y_1$') patch_y2 = mpatches.Patch(color='green', label='$y_2$') patch_y3 = mpatches.Patch(color='blue', label='$y_3$') plt.legend(handles=[patch_y1, patch_y2, patch_y3]) ymin, ymax = plt.ylim() xmin, xmax = plt.xlim() plt.subplot(2, 1, 2) font = {'family': 'serif', 'color': 'blue', 'weight': 'normal', 'size': 12, } plt.text(0.2, 0.8, r'$\frac{dy_1}{dx}= - y_1 - y_2 + \sin(x),$', fontdict=font) plt.text(0.2, 0.6,r'$\frac{dy_2}{dx}= - y_1 + y_3,$', fontdict=font) plt.text(0.2, 0.4, r'$\frac{dy_3}{dx}= - y_2 - y_2,$', fontdict=font) plt.text(0.2, 0.2, r'$y_1(a)=c_1, ' r'\quad y_2(b)=c_2, \quad y_3(b)=c_3.$', fontdict=font) plt.subplots_adjust(left=0.15) plt.show()

हमें मिलता है:

य० [०] = ०.०
y1 [0] = 1.0
y2 [0] = 0.7156448588231397
y3 [0] = 1.324566562303714
y0 [एन -1] = 0.9900000000000007
y1 [N-1] = 0.1747719838716767
y2 [एन -1] = 0.8
y3 [N-1] = 0.5000000000000001
मॉडल समस्या के लिए समय: 0.070878

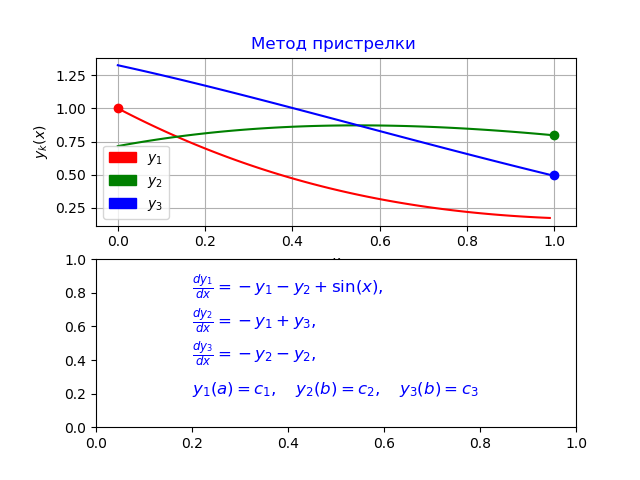
निष्कर्ष

मेरे द्वारा विकसित कार्यक्रम [3] में दी गई त्रुटि से भिन्न है, जो कि पायजॉन में लागू रन-कुट्टा - फेलबर्ग विधि के साथ लेख की शुरुआत में दिए गए odeint फ़ंक्शन के तुलनात्मक विश्लेषण की पुष्टि करता है।

संदर्भ:

1. विभेदक समीकरणों की मिश्रित प्रणालियों द्वारा परिभाषित वस्तुओं के गणितीय मॉडल का संख्यात्मक समाधान।

2. वैज्ञानिक अजगर का परिचय।

3. एन.एम. पोलाकोवा, ई.वी. शिरिवा पायथन 3. एक ग्राफिकल यूजर इंटरफेस बनाना (शूटिंग की विधि द्वारा रैखिक साधारण अंतर समीकरणों के लिए सीमा-मूल्य समस्या को हल करने के उदाहरण का उपयोग करके)। रोस्तोव-ऑन-डॉन 2017।

विभेदक समीकरणों की प्रणालियों द्वारा दी गई वस्तुओं के गणितीय मॉडल का संख्यात्मक समाधान

परिचय:

सीडीएस के संख्यात्मक समाधान के लिए विचार किए गए तरीकों और सॉफ्टवेयर पर संक्षिप्त सैद्धांतिक और वास्तविक डेटा

थ्रेड-अलग सीमा स्थितियों के साथ एक सीमा मूल्य समस्या का समाधान

निष्कर्ष

More articles: