नमस्कार, हेब्र!

तीन साल पहले, लियोनिद ज़ुकोव की साइट पर , मैंने युरे लेसकोवेक सीएस 224 डब्ल्यू एनालिसिस ऑफ़ नेटवर्क्स के पाठ्यक्रम के लिए एक लिंक दिया और अब हम इसे चैनल # class_cs2ww में अपनी आरामदायक चैट में सभी के साथ मिलकर लेंगे। कुछ दिनों में शुरू होने वाले ओपन मशीन लर्निंग कोर्स के साथ वार्म-अप के तुरंत बाद।

प्रश्न: वे वहाँ क्या पढ़ते हैं?
उत्तर: आधुनिक गणित। हम आईटी भर्ती की प्रक्रिया में सुधार का एक उदाहरण दिखाते हैं।

पाठक की बिल्ली के तहत, इस बारे में एक कहानी है कि कैसे गणित असतत गणित के लिए एक परियोजना प्रबंधक का नेतृत्व किया तंत्रिका नेटवर्क, क्यों ईआरपी और उत्पाद प्रबंधकों को बायोइनफॉरमैटिक्स पत्रिका को पढ़ना चाहिए, कैसे कनेक्शनों की सिफारिश करने का कार्य दिखाई दिया और हल किया गया है, जिन्हें ग्राफ एंबेडिंग की आवश्यकता है और वे कहां से आए हैं, साथ ही साथ राय भी। साक्षात्कारों में पेड़ों के बारे में सवालों से डरना कैसे रोकें, और यह सब क्या हो सकता है। चलो चलते हैं!

हमारी योजना इस प्रकार है:

1) cs224w क्या है
2) चेकर या सवारी
3) मुझे यह सब कैसे मिला?
4) जैव सूचना विज्ञान पत्रिका क्यों पढ़ें
5) ग्राफ एंबेडिंग क्या है और यह कहां से आया है
6) मैट्रिक्स रूप में यादृच्छिक घुमक्कड़
7) एक यादृच्छिक घुमक्कड़ की वापसी और संबंधों की ताकत
8) एक यादृच्छिक ट्रम्प का मार्ग और वेक्टर में शीर्ष
9) हमारे दिन हर किसी और हर किसी के लिए एक यादृच्छिक ट्रम्प हैं
10) ऐसे डेटा को कैसे और कहां स्टोर करना है और कहां से लाना है
११) डरना क्या
12) खिलाड़ी को मेमो

Cs224w क्या है

युरे लेसकॉव एनालिसिस ऑफ नेटवर्क्स का कोर्स स्टैनफोर्ड यूनिवर्सिटी में कम्प्यूटेशनल साइंसेज के संकाय के शैक्षिक उत्पादों की आकाशगंगा में खड़ा है। दूसरों से अंतर यह है कि कार्यक्रम बहुत व्यापक मुद्दों को शामिल करता है। यह अंतःविषय प्रकृति है जो साहसिक कार्य को चुनौती देती है। पुरस्कार जटिल प्रणालियों के वर्णन के लिए सार्वभौमिक भाषा है - ग्राफ सिद्धांत, जिसे दस सप्ताह में निपटाया जा सकता है।

इस कोर्स की लागत बहुत अधिक नहीं है, लेकिन खनन विशाल डेटा सेट्स ग्रेजुएट सर्टिफिकेट प्रोग्राम खोलता है, जिसमें अभी भी बहुत सारे उपहार हैं।

साहसिक कार्य में दूसरा है एंड्रयू यून की CS229 मशीन लर्निंग, जो अनावश्यक रूप से विज्ञापित है।

इसके बाद CS246 माइनिंग मैसिव डेटा सेट्स Jure Leskoveka है, जिसमें इच्छा रखने वालों को MapReduce और Spark पर आराम करने के लिए आमंत्रित किया जाता है।

क्रिस मैनिंग ने भोज को समाप्त किया CS276 सूचना पुनर्प्राप्ति और वेब खोज।

एक बोनस के रूप में, CS246H खनन विशाल डेटा सेट: Hadoop लैब्स को विशेष रूप से उन लोगों के लिए डिज़ाइन किया गया है जो कम थे। फिर से Yure पर जाएँ।

सामान्य तौर पर, वे वादा करते हैं कि जिन लोगों ने कार्यक्रम पास कर लिया है, वे इंटरनेट पर जानकारी के लिए पर्याप्त कौशल और ज्ञान प्राप्त करेंगे (बिना किसी Google और उनके जैसे अन्य)।

सवारी या चेकर

एक बार, मेरे नेता और संरक्षक, उस समय - यूक्रेनी नेस्ले में एसटीओ, मुझे समझा रहा था, युवा और महत्वाकांक्षी, एमबीए बनने के लिए भी एक स्टार बनने की कोशिश कर रहा था, सच्चाई यह है कि अनुभव और ज्ञान श्रम बाजार में खरीद और बिक्री कर रहे हैं, और नहीं डिप्लोमा और परीक्षण के परिणाम।

ऊपर वर्णित विशेषज्ञता को प्रतीकात्मक $ 18,900 के लिए ऑनलाइन पूरा किया जा सकता है।

औसतन, एक साहसिक कार्य में 1-2 साल लगते हैं, लेकिन 3. से अधिक नहीं। एक प्रमाण पत्र प्राप्त करने के लिए, आपको कम से कम बी (3.0) की रेटिंग के साथ सभी पाठ्यक्रमों को पूरा करना होगा।

एक और तरीका है।

Jure Leskovek के पाठ्यक्रमों की सभी सामग्रियों को खुले तौर पर और बहुत तेज़ी से प्रकाशित किया जाता है। इसलिए, जो लोग चाहते हैं वे किसी भी सुविधाजनक समय में, क्षमताओं के साथ लोड का समन्वय कर सकते हैं। विशेष रूप से उपहार में मुझे एडवेंचर मोड की कोशिश करने की सलाह देते हैं "यह स्टैनफोर्ड है, शहद!" - पाठ्यक्रम के समानांतर गुजरना - व्याख्यान के वीडियो कुछ दिनों के भीतर पोस्ट किए जाते हैं, अतिरिक्त साहित्य तुरंत उपलब्ध होता है, होमवर्क और समाधान धीरे-धीरे खुलते हैं।

इस सीजन में, हैबे पर ओपन मशीन लर्निंग कोर्स के अंत के बाद, जो वार्म-अप के रूप में लेने के लिए उपयोगी है, हम समर्पित चैनल वर्ग # cs_cs224w ods.ai में एक दौड़ की व्यवस्था करेंगे।

यह कौशल के निम्नलिखित सेट की सिफारिश की है:

• गैर-तुच्छ कार्यक्रमों को लिखने के लिए पर्याप्त स्तर पर कम्प्यूटेशनल विज्ञान के बुनियादी ढांचे।
• प्रायिकता सिद्धांत के मूल सिद्धांत।
• रैखिक बीजगणित के मूल तत्व।

मुझे यह सब कैसे मिला?

वह अपने लिए जीए, परेशान नहीं हुए। प्रबंधित एसएपी कार्यान्वयन परियोजनाएं। कई बार - उन्होंने अपने मुख्य विशेषज्ञता - और सीआरएम ट्विस्टेड नट्स में एक खेल प्रशिक्षक के रूप में काम किया। आप कह सकते हैं लगभग किसी को नहीं छुआ। मैं स्व-शिक्षा में लगा हुआ था। कुछ बिंदु पर, मैंने व्यावसायिक परिवर्तन (या संगठनात्मक परिवर्तन करने) के क्षेत्र में विशेषज्ञता का फैसला किया। परिवर्तन से पहले और बाद में संगठनों के विश्लेषण का कार्य इस कार्य का एक महत्वपूर्ण हिस्सा है। यह जानना कि कहां और कहां बदलना बहुत मदद करता है। लोगों के बीच संबंधों को समझना एक महत्वपूर्ण सफलता कारक है। उन्होंने शोध संगठनों के लिए "नरम" कार्यप्रणाली का अध्ययन करने में कई साल बिताए, लेकिन वे अभी भी इस सवाल से संतुष्ट नहीं थे: "कौन किसे उठाएगा: मुख्य लेखाकार का कमांडर-इन-चीफ, या यह स्टोरहाउस के बाकी हिस्सों की तुलना में मजबूत है?" मैं कई वर्षों से सोच रहा था। मैं सुनिश्चित करने के लिए उपाय की तलाश में हूं।

2014 एक महत्वपूर्ण मोड़ था, जब मैंने एमबीए के अपने सपनों को त्याग दिया और लिस्बन विश्वविद्यालय के नए विश्वविद्यालय में सांख्यिकी और सूचना प्रबंधन को चुना (पहले और अब जीवित पॉलिटेक्निक यूनिवर्सिटी के मौजूदा सिस्टम के मौजूदा दूरसंचार विभाग) दूसरा उच्चतम (मैं ड्रम रोल सुनता हूं)। + सेना में संचार विभाग)।

दूसरे जादूगर के पहले सेमेस्टर में, उन्होंने सोशल नेटवर्क के विश्लेषण की कोशिश की - ग्राफ सिद्धांत के अनुप्रयोगों में से एक। यह तब था जब मैंने सीखा कि यह कुछ ऐसा था, यह पता चला, एल्गोरिदम हैं जो समस्याओं को हल करते हैं जैसे कि नई तकनीकों के कार्यान्वयन के खिलाफ किसी के साथ दोस्त होंगे, लेकिन मुझे पहले पता नहीं था और मेरे सिर को सूख गया, मेरे दिमाग में लोगों के कनेक्शन का विश्लेषण - यह वास्तव में इस से आ रही है। यह संयोग से निकला कि पहले चरणों के बाद, नेटवर्क का विश्लेषण, डेटा और मशीन सीखने की निरंतर खुदाई है, या तो एक शिक्षक के साथ या बिना।

पहले, पर्याप्त क्लासिक्स थे।

मुझे और चाहिए था। एंबेडिंग से निपटने के लिए (और उनके कार्यों के लिए मरिंका ज़िटनिक के काम में कटौती करने के लिए), मुझे गहरी सीखने में तल्लीन करना पड़ा, जिसे उंगलियों पर डीप लर्निंग कोर्स द्वारा बहुत मदद मिली। जिस गति से लेसकॉव समूह नया ज्ञान बनाता है, उसे देखते हुए, प्रबंधकीय कार्यों को स्वचालित रूप से हल करने के लिए, यह केवल उनके काम की निगरानी करने के लिए पर्याप्त है।

जैव सूचना विज्ञान पत्रिका क्यों पढ़ें

टीम बनाना कोई आसान काम नहीं है। जिसे एक ही नाव में नहीं डाला जाना चाहिए, वह दबाव वाले मुद्दों में से एक है। खासकर तब जब चेहरे नए हों। और क्षेत्र अपरिचित है। और दूर के तटों पर जाने के लिए आपको एक नाव की नहीं, बल्कि एक पूरी फ़्लाटिला की ज़रूरत है। और रास्ते में, नौकाओं और उनके बीच दोनों में निकट संपर्क आवश्यक है। एसएपी कार्यान्वयन के सामान्य कार्यदिवस, जब ग्राहक को मॉड्यूल की एक गुच्छा से अपनी बारीकियों के लिए कॉन्फ़िगर की गई प्रणाली को वितरित करने की आवश्यकता होती है, और परियोजना योजना में हजारों लाइनें शामिल होती हैं। अपने सभी कार्यों के लिए, उन्होंने कभी किसी को काम पर नहीं रखा - उन्होंने हमेशा एक टीम जारी की। आप एक परियोजना प्रबंधक हैं, आपके पास शक्तियां हैं, और चारों ओर मुड़ें हैं। कुछ इस तरह। बाहर मुड़ गया।

जीवन उदाहरण:

मैंने खुद साक्षात्कार नहीं किया, लेकिन मैंने इसके लिए टाइमलाइड्स आवंटित किया। और संसाधनों के लिए - मुझसे मांग। और टीम के नए सदस्यों का एकीकरण भी परियोजना प्रबंधक की जिम्मेदारी है। मुझे विश्वास है कि कई इस बात से सहमत होंगे कि उम्मीदवारों की सूची जितनी बेहतर तैयार होगी, सभी प्रतिभागियों के लिए प्रक्रिया उतनी ही सुखद होगी। हम इस कार्य पर विस्तार से विचार करेंगे।

प्राकृतिक आलस्य की आवश्यकता है - स्वचालित करने का एक तरीका खोजें। मिल गया। मैं साझा करता हूं।

प्रबंधन सिद्धांत का एक सा। Adizes कार्यप्रणाली एक बुनियादी सिद्धांत पर आधारित है: संगठन, जीवित जीवों की तरह, अपने स्वयं के जीवन चक्र होते हैं और विकास और उम्र बढ़ने के दौरान पूर्वानुमान और दोहराव वाले व्यवहार अभिव्यक्तियों को प्रदर्शित करते हैं। संगठनात्मक विकास के प्रत्येक चरण में, कंपनी को समस्याओं के एक विशिष्ट सेट की उम्मीद है। कंपनी का प्रबंधन उन्हें कितनी अच्छी तरह से संभालता है, एक मंच से मंच तक एक स्वस्थ संक्रमण के लिए आवश्यक परिवर्तन को सफलतापूर्वक कैसे करता है, और इस संगठन की अंतिम सफलता या विफलता को निर्धारित करता है।

मैं लगभग दस साल से यित्ज़ाक एडिज़ के विचारों से परिचित हूं और कई मामलों में सहमत हूं।

कर्मचारियों की व्यक्तित्व - विटामिन की तरह - कुछ स्थितियों में सफलता को प्रभावित करती है। एक उद्योग से आगे बढ़ने, दूसरे में असफल होने के सफल नेता, इसके उदाहरण हैं। यह बदतर होता है। उदाहरण के लिए, मारिसा मेयर, जिन्होंने Google खोज को उठाया, याहू को गिरा दिया। वारेन बफेट का कहना है कि वह शायद ही बांग्लादेश में पैदा होने में सफल रहे होंगे। पर्यावरण और इसमें सहभागिता के तरीके एक महत्वपूर्ण कारक हैं।

किसी जीवित व्यक्ति पर प्रयोगों से पहले जटिलताओं की भविष्यवाणी करना अच्छा होगा, है ना?

इस रूपरेखा में, जर्नल बायोइनफॉरमैटिक्स में प्रकाशित Marinka itnik का अगला अध्ययन निहित है। दवाओं के संयुक्त उपयोग के साथ दुष्प्रभावों की भविष्यवाणी करने का कार्य गणितीय रूप से प्रबंधकीय के करीब है। सभी ग्राफ भाषा की बहुमुखी प्रतिभा के लिए धन्यवाद। आइए इसे और अधिक विस्तार से विचार करें।

डेकागन ग्राफ कंफ्यूजनल नेटवर्क - मल्टीमॉडल नेटवर्क में कनेक्शन की भविष्यवाणी करने के लिए एक उपकरण।

विधि में प्रोटीन-प्रोटीन, ड्रग-प्रोटीन इंटरैक्शन और ड्रग्स के संयोजन से साइड इफेक्ट्स के एक बहु-विषयक ग्राफ का निर्माण होता है, जो ड्रग-ड्रग संबंध हैं, जहां प्रत्येक साइड इफेक्ट एक निश्चित प्रकार का एक किनारा है। Decagon एक विशिष्ट प्रकार के साइड इफेक्ट की भविष्यवाणी करता है, यदि कोई हो, जो नैदानिक ​​तस्वीर में दिखाई देता है।

यह आंकड़ा जीनोम और जनसंख्या के आंकड़ों से प्राप्त दुष्प्रभावों का एक उदाहरण दिखाता है। कुल में - 964 विभिन्न प्रकार के साइड इफेक्ट्स (री प्रकार की पसलियों द्वारा इंगित, i = 1, ..., 964)। मॉडल में अतिरिक्त जानकारी प्रोटीन और दवाओं के गुणों के वैक्टर के रूप में प्रस्तुत की जाती है।

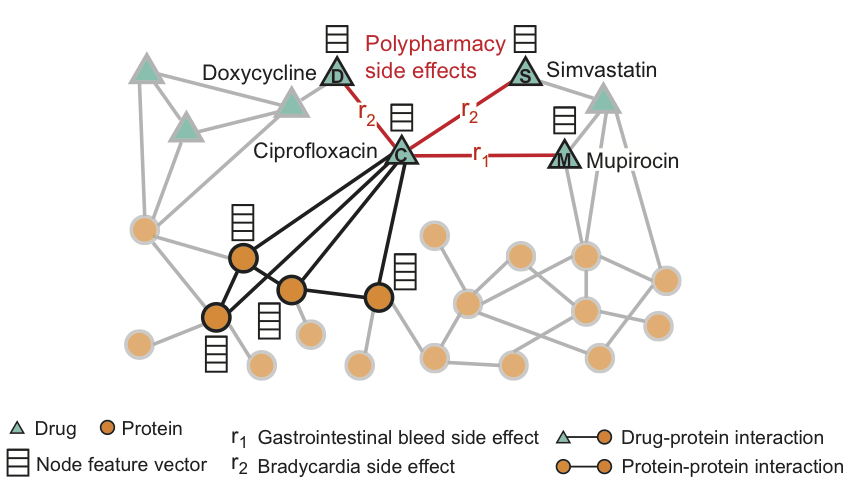
दवा सिप्रोफ्लोक्सासिन (नोड सी) के लिए, ग्राफ़ में हाइलाइट किए गए पड़ोसी चार प्रोटीन और तीन अन्य दवाओं पर प्रभाव को दर्शाते हैं। हम देखते हैं कि सिप्रोफ्लोक्सासिन (नोड सी), डॉक्साइक्लाइन (नोड डी) या सिमावास्टिन (नोड एस) के साथ समवर्ती रूप से लिया जाता है, हृदय गति को धीमा करने के साइड इफेक्ट का खतरा बढ़ जाता है (आर 2 की तरह एक साइड इफेक्ट), और मुपीरोसीन (एम) के साथ संयोजन - जठरांत्र संबंधी मार्ग (साइड इफेक्ट प्रकार आर 1) के रक्तस्राव का खतरा बढ़ जाता है।

समवर्ती उपयोग से साइड इफेक्ट्स की पहचान करने के लिए ड्रग जोड़े और साइड इफेक्ट्स (लाल रंग में दिखाया गया है) के बीच Decagonts संघों की भविष्यवाणी करता है, उन दुष्प्रभावों को जो अलग से जोड़ी से किसी भी दवा के साथ जुड़ा नहीं हो सकता है।

डेक्गन कन्फ्यूज़नल न्यूरल नेटवर्क ग्राफ आर्किटेक्चर:

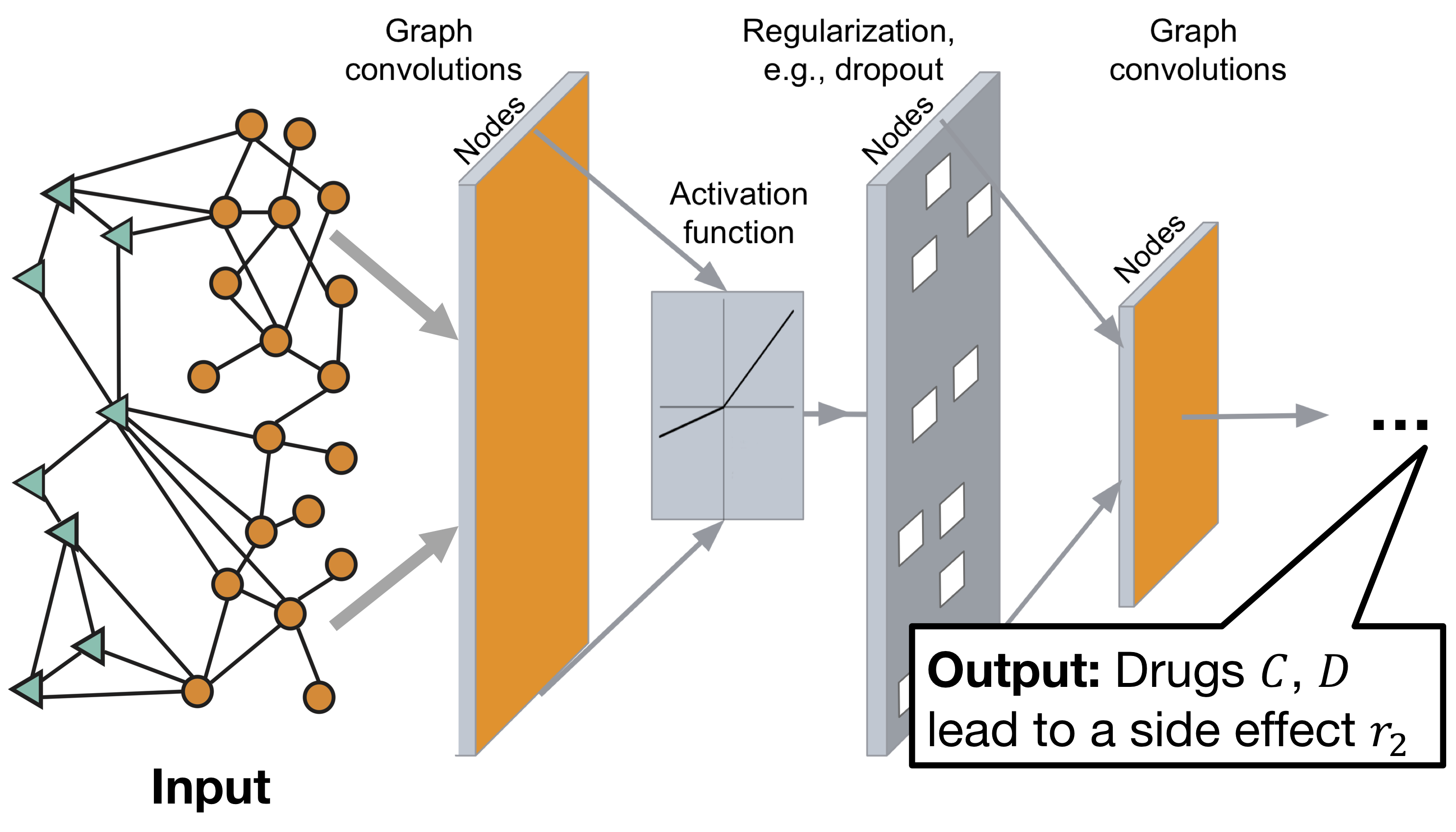
मॉडल में दो भाग होते हैं:

एनकोडर: ग्राफ कंफ्यूशनल नेटवर्क (GCN) एक ग्राफ प्राप्त करता है और नोड्स के लिए एम्बेड करता है,
विकोडक: एक तन्य कारक मॉडल जो साइड इफेक्ट्स का पता लगाने के लिए इन एम्बेडिंग का उपयोग करता है।

अधिक जानकारी परियोजना की वेबसाइट या नीचे दी जा सकती है।

महान, लेकिन टीम बिल्डिंग के लिए यह कैसे टाई है?

कुछ इस तरह ।

यहां, वर्णित के समान अनुसंधान के क्षेत्र में सहज महसूस करने के लिए, यह विज्ञान के ग्रेनाइट को खोदने के लायक है। सच है, खुदाई गहन रूप से होगी - ग्राफ सिद्धांत सक्रिय रूप से विकसित हो रहा है। यही कारण है कि यह प्रगति का भाला है - कुछ लोग वहां सहज हैं।

डेकागन के कामकाज के विवरण को समझने के लिए, हम इतिहास में भ्रमण करेंगे।

ग्राफ़ एम्बेडिंग क्या है और यह कहाँ से आया है

मैं पिछले चार वर्षों में रेखांकन पर कनेक्शन की भविष्यवाणी की समस्याओं को हल करने के लिए उन्नत तरीकों के सेट में बदलाव का निरीक्षण करने के लिए हुआ। यह मजेदार था। लगभग एक परी कथा की तरह - आगे, बदतर। विकास ने उन आंकड़ों से मार्ग का अनुसरण किया जो ग्राफ़ के शीर्ष से यादृच्छिक घुमक्कड़ के लिए पर्यावरण का निर्धारण करते हैं, फिर वर्णक्रमीय तरीके (मैट्रिक्स विश्लेषण) दिखाई दिए, और अब तंत्रिका नेटवर्क।

हम रिश्तों की भविष्यवाणी की समस्या को तैयार करते हैं:

एक अप्रत्यक्ष ग्राफ पर विचार करें$$ $ इनलाइन $ \ start {align *} G (V, E) \ end {align *} $ इनलाइन $ जहाँ
$$$ इनलाइन $ \ start {align *} V \ end {align *} $ इनलाइन $ - कई चोटियाँ$$ $ इनलाइन $ \ start {align *} v \ end {align *} $ इनलाइन $ ।
$$$ इनलाइन $ \ start {align *} E \ end {align *} $ इनलाइन $ - कई पसलियां$$ $ इनलाइन $ \ start {align *} e (u, v) \ end {align *} $ इनलाइन $ चोटियों को जोड़ना$$ $ इनलाइन $ \ start {align *} u \ end {align *} $ इनलाइन $ और$$ $ इनलाइन $ \ start {align *} v \ end {align *} $ इनलाइन $ ।

हम सभी संभावित किनारों के सेट को परिभाषित करते हैं$$ $ इनलाइन $ ई ^ {{हीरा} $ इनलाइन $ इसकी शक्ति
$$$ इनलाइन $ \ start {संरेखित *} | ई ^ {\ हीरा} | & = \ frac {| V | * | (| V | - 1)} {2} \\ \ end {संरेखित}} इनलाइन $ जहाँ
$$$ इनलाइन $ \ start {align *} | V | = n \ end {संरेखित *} $ इनलाइन $ , कोने की संख्या है।

जाहिर है, कई गैर-मौजूद किनारों को व्यक्त किया जा सकता है$$ $ इनलाइन $ \ start {align *} \ overline {E} = E ^ {\ Diamond} - E \ end {align *} $ इनलाइन $ ।

हम सेट में मान लेते हैं$$ $ इनलाइन $ \ start {align *} \ overline {E} \ end {align *} $ इनलाइन $ भविष्य में दिखाई देने वाले लिंक या लिंक छूट गए हैं, और हम उन्हें ढूंढना चाहते हैं।

किसी फ़ंक्शन को परिभाषित करने के लिए समाधान नीचे आता है$$ $ इनलाइन $ \ start {align *} D (u, v) \ end {align *} $ इनलाइन $ ग्राफ के कोने के बीच की दूरी, ग्राफ की संरचना के लिए अनुमति देता है$$ $ इनलाइन $ \ start {संरेखित *} जी (t_0, t_0 ^ \ सितारा) \ अंत {संरेखित *} इनलाइन $ समय की अवधि पर सेट करें$$ $ इनलाइन $ \ start {संरेखित *} (t_0, t_0 ^ \ सितारा) \ अंत {संरेखित}} $ इनलाइन $ किनारों की उपस्थिति की भविष्यवाणी करें$$ $ इनलाइन $ \ start {संरेखित *} जी (t_1, t_1 ^ \ सितारा) \ अंत {संरेखित}} $ इनलाइन $ सीमा में$$ $ इनलाइन $ \ start {संरेखित *} (t_1, t_1 ^ \ सितारा) \ अंत {संरेखित}} $ इनलाइन $ ।

2000 में संयुक्त जीन अभिव्यक्ति के अध्ययन के संदर्भ में रिश्तों की भविष्यवाणी करने के कार्य के लिए क्लस्टरिंग से आगे बढ़ने का प्रस्ताव करने वाले पहले प्रकाशनों में से एक था (जैसा कि आप अनुमान लगा सकते हैं) 2000 में जैव सूचना विज्ञान। पहले ही 2003 में, जॉन क्लेनबर्ग का एक लेख एक सामाजिक नेटवर्क में पूर्वानुमान कनेक्शन की समस्या को हल करने के लिए प्रासंगिक तरीकों के अवलोकन के साथ प्रकाशित किया गया था। उनकी पुस्तक " नेटवर्क्स, क्राउड्स एंड मार्केट्स: रीज़निंग अबाउट अ हाइली कनेक्टेड वर्ल्ड " एक टेक्स्टबुक है जिसे सीएस 224w कोर्स के दौरान पढ़ने की सलाह दी जाती है, अधिकांश अध्याय आवश्यक रीडिंग सेक्शन में सूचीबद्ध हैं।

एक लेख को एक संकीर्ण क्षेत्र में ज्ञान का टुकड़ा माना जा सकता है, जैसा कि हम देखते हैं, पहले तरीकों का वर्गीकरण छोटा था और इसमें शामिल थे:

• ग्राफ पड़ोसियों पर आधारित तरीके - और इनमें से सबसे स्पष्ट है आम पड़ोसियों की संख्या।

हम परिभाषा देते हैं:

शिखर$$ $ इनलाइन $ यू $ इनलाइन $ शीर्ष के लिए एक ग्राफ पड़ोसी है$$ $ इनलाइन $ v $ इनलाइन $ अगर पसली$$ $ इनलाइन $ ई (यू, वी) \ ई ई $ इनलाइन $ में ।

हम निरूपित करते हैं$$ $ इनलाइन $ \ Gamma (u) $ इनलाइन $ कई पड़ोसी चोटियों पर हैं$$ $ इनलाइन $ यू $ इनलाइन $ ।

फिर चोटियों के बीच की दूरी$$ $ इनलाइन $ यू $ इनलाइन $ और$$ $ इनलाइन $ v $ इनलाइन $ के रूप में लिखा जा सकता है

$$$ इनलाइन $ D_ {CN} (u, v) = \ Gamma (u) \ cap \ Gamma (v) इनलाइन $ ।

सहज रूप से, दो चोटियों के पड़ोसियों के सेट का अधिक से अधिक चौराहा, उनके बीच संबंध होने की अधिक संभावना है, उदाहरण के लिए, दोस्तों के दोस्तों के साथ सबसे नए परिचित होते हैं।

अधिक उन्नत अनुमान - जैक्वार्ड गुणांक$$ $ इनलाइन $ D_J (u, v) = \ frac {\ Gamma (u) \ cap \ Gamma (v)} {\ Gamma (u) \ cup \ Gamma (v)} $ इनलाइन $ (जो पहले से ही सौ साल पुराना था) और हाल ही में (उस समय) प्रस्तावित दूरी एडमिक / अडार$$ $ इनलाइन $ D_ {AA} (u, v) = \ sum_ {x \ in \ Gamma (u) \ cap \ Gamma (v)} \ frac {1} {\ log | \ Gamma (x) |} $ inline $ सरल परिवर्तनों के माध्यम से विचार विकसित करें।

• एक ग्राफ के साथ रास्तों पर आधारित तरीके - विचार यह है कि एक ग्राफ पर दो कोने के बीच का सबसे छोटा रास्ता उन दोनों के बीच संबंध की संभावना से मेल खाता है - पथ जितना छोटा होगा, मौका उतना ही अधिक होगा। आप आगे जा सकते हैं और न केवल सबसे छोटे रास्ते को ध्यान में रख सकते हैं, बल्कि चोटियों के जोड़े के बीच अन्य सभी संभावित रास्ते भी हैं, उदाहरण के लिए, पथों को तौलना, जैसा कि काट्ज दूरी करता है। पहले से ही, एक यादृच्छिक ट्रम्प की अपेक्षित पथ लंबाई का उल्लेख किया गया है - फेसबुक मित्र सिफारिश विधि के अग्रदूत।

पूर्वानुमान की गुणवत्ता का अनुमान लगाएं:

• प्रत्येक जोड़ी के लिए$$ $ इनलाइन $ (u, v) $ इनलाइन $ हर कोई नहीं पसली$$ $ इनलाइन $ e (u, v) \ in \ overline {E} $ इनलाइन $ दूरी की गणना करें$$ $ इनलाइन $ डी (यू, वी) $ इनलाइन $ ग्राफ पर$$ $ इनलाइन $ G (t_0, t_0 ^ \ star) $ इनलाइन $ ।
• जोड़े को क्रमबद्ध करें$$ $ इनलाइन $ (u, v) $ इनलाइन $ उतरती दूरी$$ $ इनलाइन $ डी (यू, वी) $ इनलाइन $ ।
• दूर ले जाओ$$ $ इनलाइन $ एम $ इनलाइन $ उच्चतम मूल्यों के साथ जोड़े हमारे पूर्वानुमान हैं।
• आइए देखें कि कितने अनुमानित किनारों में दिखाई दिया$$ $ इनलाइन $ G (t_1, t_1 ^ \ star) $ इनलाइन $ ।

यह याद रखना महत्वपूर्ण है कि आम पड़ोसियों की संख्या और एडमिक / एडार दूरी शक्तिशाली विधियां हैं जो केवल लिंक संरचना के लिए पूर्वानुमान गुणवत्ता के मूल स्तर को निर्दिष्ट करती हैं, और यदि आपकी सिफारिश प्रणाली कमजोर परिणाम दिखाती है, तो कुछ गलत है।

आम तौर पर, ग्राफ एम्बेडिंग ट्रांसफ़ॉर्म फ़ंक्शन का उपयोग करके मशीन सीखने के कार्यों के लिए कॉम्पैक्ट रूप से ग्राफ़ का प्रतिनिधित्व करने का एक तरीका है$$ $ इनलाइन $ \ start {align *} \ phi: G (V, E) \ longmapsto \ mathbb {R} ^ d \ end {align *} $ इनलाइन $ ।

हमने इनमें से कई कार्यों की जांच की, जो पहले के सबसे प्रभावी थे। एक विस्तृत सूची क्लेनबर्ग के एक लेख में वर्णित है। जैसा कि हम समीक्षा से देख सकते हैं, तब भी उन्होंने उच्च-स्तरीय विधियों को लागू करना शुरू किया, जैसे कि मैट्रिक्स अपघटन, प्रारंभिक क्लस्टरिंग और कम्प्यूटेशनल भाषाविज्ञान के शस्त्रागार से उपकरण। पंद्रह साल पहले, सबकुछ बस शुरुआत थी। एंबेडिंग एक आयामी थे।

मैट्रिक्स के आकार का यादृच्छिक घुमक्कड़

एक ही ग्राफ एम्बेडिंग के रास्ते में अगला मील का पत्थर यादृच्छिक चलने के तरीकों का विकास था। दूरी की गणना के लिए नए सूत्रों का आविष्कार और औचित्य साबित करने के लिए, स्पष्ट रूप से, एक विराम बन गया। कुछ अनुप्रयोगों में, ऐसा लगता है कि आपको बस मौके पर भरोसा करना है और आवारा लोगों पर भरोसा करना है।

हम परिभाषा देते हैं:

ग्राफ आसन्न मैट्रिक्स$$ $ इनलाइन $ जी $ इनलाइन $ कोने की एक परिमित संख्या के साथ$$ $ इनलाइन $ n $ इनलाइन $ (1 से गिने गए$$ $ इनलाइन $ n $ इनलाइन $ ) एक वर्ग मैट्रिक्स है$$ $ इनलाइन $ एक $ इनलाइन $ आकार$$ $ इनलाइन $ n \ गुना n $ इनलाइन $ जिसमें तत्व का मूल्य है$$ $ इनलाइन $ a_ {ij} $ इनलाइन $ वजन के बराबर$$ $ इनलाइन $ w_ {ij} $ इनलाइन $ रिब्स$$ $ इनलाइन $ ई (i, j) $ इनलाइन $ ।

नोट: यहां हम जानबूझकर पहले इस्तेमाल किए गए शीर्ष संकेतक से दूर चले गए हैं$$ $ इनलाइन $ यू, वी $ इनलाइन $ और हम रेखीय बीजगणित और सामान्य रूप से, मैट्रिसेस के साथ काम करने के लिए परिचित संकेतन का उपयोग करेंगे$$ $ इनलाइन $ i, j $ इनलाइन $ ।

हम मानी गई अवधारणाओं को स्पष्ट करते हैं:

चलो$$ $ इनलाइन $ जी $ इनलाइन $ - चार कोने का ग्राफ$$ $ इनलाइन $ \ {A, B, C, D \} $ इनलाइन $ पसलियों द्वारा जुड़ा हुआ है।

निर्माणों को सरल बनाने के लिए, हम मानते हैं कि हमारे ग्राफ के किनारे द्विदिश हैं, अर्थात्।$$ $ इनलाइन $ \ forall e (i, j) \ E में, \ E में मौजूद है (j, i) \ e में भूमि w_ {ij} = w_ {ji} $ inline $ ।

$$$ इनलाइन $ e (A, B), w_ {AB} = 1; \\ e (B, C), w_ {BC} = 2; \\ e (A, C), w_ {AC} = 3; \ _ \ e (B, C), w_ {BC} = 1. $ इनलाइन $

हम किनारों के सेट का प्रतिनिधित्व करते हैं:$$ $ इनलाइन $ ई $ इनलाइन $ - नीले रंग में, और$$ $ इनलाइन $ \ overline {E} $ इनलाइन $ - हरे रंग में।



$$$ इनलाइन $ \ start {align *} A = \ left [\ start {मैट्रिक्स} 0 & 1 & 3 & 0 \\ 1 & 0 & 2 & 1 & \ _ 3 और 2 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \ एंड {मैट्रिक्स} \ राइट] \ एंड {एलाइन *} $ इनलाइन $

मैट्रिक्स के रूप में एक ग्राफ लिखना दिलचस्प संभावनाओं को खोलता है। उन्हें प्रदर्शित करने के लिए, सेर्गेई ब्रिन और लैरी पेज के काम पर एक नज़र डालें, और देखें कि पेजरैंक, ग्राफ वर्टिकल रैंकिंग के लिए एक एल्गोरिथ्म, अभी भी Google खोज का एक महत्वपूर्ण हिस्सा कैसे है।

पेजरैंक - इंटरनेट पर बहुत अच्छे पन्नों को खोजने के लिए गढ़ा गया। एक पेज को अच्छा माना जाता है यदि वह अन्य अच्छे पृष्ठों द्वारा सराहा (जुड़ा हुआ) है। अधिक पृष्ठों में इसके लिंक होते हैं, और उनकी रेटिंग जितनी अधिक होती है, किसी दिए गए पृष्ठ के लिए उच्च पेजरैंक।

मार्कोव श्रृंखलाओं का उपयोग करते हुए विधि की व्याख्या पर विचार करें ।

हम एक परिभाषा देते हैं:

एक शीर्ष की डिग्री (डिग्री) कई पड़ोसियों की शक्ति है:
$$$d_i = |\Gamma(i)|$,

इन-डिग्री और बाहर डिग्री कर रहे हैं। हमारे उदाहरण के लिए, वे समकक्ष हैं।

हम नियम द्वारा निर्देशित एक भारित आसन्न मैट्रिक्स का निर्माण करते हैं:
$$मiज ={१dj ∀i,j⟺मैं∈गामा(जे),0∀मैं,जे⟺i∉Γ(j).$\begin{align*}M_{ij} = \left\{ \begin{matrix} \frac{1}{d_j} & \forall i,j \iff i \in \Gamma(j), \\ 0 & \forall i,j \iff i \notin \Gamma(j). \end{matrix} \right.\end{align*}$

$$M=[01312012012112130001300]$\begin{align*}M = \left[ \begin{matrix} 0 & \frac{1}{3} & \frac{1}{2} & 0 \\ \frac{1}{2} &0 & \frac{1}{2} & 1 \\ \frac{1}{2} & \frac{1}{3} & 0 & 0\\ 0 & \frac{1}{3} & 0& 0 \end{matrix} \right]\end{align*}$

,$$$M$ 1 (..$$$M$ — " ").$$$j$$$$i \in \Gamma(j)$ ।

$$$r_i$PageRank$$$i$ ,$$$d_i$ . PageRank$$$j$ कैसे

$$

$$r_j = \sum_{i \to j}\frac{r_i}{d_i}$$

,$$$i$$$$j$ PageRank, (.. PageRank), .

PageRank$$$\begin{align*}r = [r_1, r_2, ..., r_n]^T \end{align*}$ — :

$$

$$r = Mr$$

-, ( ).$$$t$$$$i$$$$t+1$$$$j \in \Gamma(i)$ , , — .

हम निरूपित करते हैं$$$p(t)$ ,$$$i$ समय पर$$$t$ ।$$$p(t)$ — , 1.

,$$$M_{ij}$ —$$$j$$$$i$ ,$$$j$ और$$$p_j(t)$ — ,$$$j$$$$t$ । ,$$$i$

$\$\$display\$\$p\_i(t+1)\; =\; M\_\{i1\}p\_1(t)\; +\; M\_\{i2\}p\_2\; +\; .$। । + M_{in}p_n(t)$$display$$

,

$$

$$p(t + 1) = Mp(t)$$

- ,$$$p(t + 1) = p(t)$ ,$$$p(t)$ — . , PageRank$$$r = Mr$ । —$$$r$ PageRank — !

$$$r$PageRank . ,$$$r^{(t0)} = [1/n, 1/n, ..., 1/n]^T$$$$r^{(t+1)} = Mr^{(t)}$$$$t$ , , ..$$$||r^{(t+1)} - r^{(t)}||_1< \epsilon</script=/> जहाँ<math><span class="MathJax_Preview" style="color: inherit;"><span class="MJXp-math" id="MJXp-Span-905"><span class="MJXp-mi MJXp-italic" id="MJXp-Span-906">ϵ</span></span></span><span class="MathJax_SVG MathJax_SVG_Processed" id="MathJax-Element-94-Frame" tabindex="0" style="font-size: 100%; display: inline-block;"><svg xmlns:xlink="http://www.w3.org/1999/xlink" width="0.944ex" height="1.455ex" viewBox="0 -520.7 406.5 626.5" role="img" focusable="false" style="vertical-align: -0.246ex;"><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"><use xlink:href="https://translate.googleusercontent.com/translate_c?depth=1&amp;rurl=translate.google.com&amp;sl=ru&amp;sp=nmt4&amp;tl=hi&amp;u=https://habr.com/ru/company/ods/blog/418727/&amp;usg=ALkJrhglRRSbcfQU-ZYvwup3O7-xcBS7Hw#MJMATHI-3F5" x="0" y="0"/></g></svg></span><script type="math/tex" id="MathJax-Element-94">\epsilon$ — . ( ,$$$||x||_1 = \sum_{k} |x_k|$ —$$$L_1$ , ).$$$r^{(t+1)}$ Page Rank . , 20-30 .

.

"" :

• .. " " — , — , PageRank . . .
• — — PageRank . - .$$$r$ .

20 , !

-$$$\beta$ ,$$$1 - \beta$ — .$$$1 - \beta \approx 0.15$ , यानी। - 5-7 . — . PageRank :

$$

$$r_j = \sum_{i \to j}\beta\frac{r_i}{d_i} + (1-\beta)\frac{1}{n}$$

( , )

$$$M$,

$$

$$M^{\star} = \beta M + (1-\beta) [1/n]_{n×n}$$

.$$$r = M^{\star}r$ . , , 37-38 14- cs224w 2017 , , Pinterest ( ).

. ?

:

• ;
• ;
• , .

PageRank. , , - , - .

— .

.

, . - ? 2006 .

:

, -$$$G$ , - .

$$$i$$$$k$$$$f^{(i)} = [f_1, f_2, ..., f_k]^T$।



,$$$f_1$ , , .

, , . - . , — (, ). , IT- , ( ) — .

, , — , ,$$$A$ और$$$C$ — .

, — .

- , Kaggle Hackerrank, , , (, ).

:

$$$S_k(x)$$$$x$$$$k$,$$$G$ :

$$∀i∈V,i∈Sk(x)⟺f(i)k=x$\forall i \in V, i \in S_k(x) \iff f^{(i)}_{k} = x$

:

$$Mpij={βMij+1−β|Sk(x)|∀i,j⟺i∈Sk(x),βMij∀i,j⟺i∉Sk(x).$\begin{align*}M^{p}_{ij} = \left\{ \begin{matrix} \beta M_{ij} + \frac{1-\beta}{|S_k(x)|} & \forall i,j \iff i \in S_k(x), \\ \beta M_{ij} & \forall i,j \iff i \notin S_k(x). \end{matrix} \right.\end{align*}$

$$$\begin{align*} r = M^{p} r \end{align*}$$$$\begin{align*} r \end{align*}$, .$$$\begin{align*} r \end{align*}$ PageRank — . ,$$$\begin{align*} r \end{align*}$ — .

80% Pinterest.

,$$$\begin{align*}|S_k(x)| = 1\end{align*}$ कहा जाता है, रेस्टार्ट्स के साथ रैंडम वॉक - घुमक्कड़ वापस आते हैं और हमारे लिए ब्याज के एक शिखर पर वापस आते हैं। नतीजतन, हमें ग्राफ के प्रत्येक शीर्ष के लिए निकटता का एक माप मिलता है जो केवल एक के संबंध में है। और यह आदमिक / अडार दूरी की अनुमति से बेहतर कनेक्शन की भविष्यवाणी की समस्या को हल करता है।

और सुधार जोड़ें:

याद है कि पसलियों$$ $ इनलाइन $ \ start {align *} e (i, j) \ _ in \ G में जी \ _ {align *} $ इनलाइन $ हमारे ग्राफ में वज़न है$$ $ इनलाइन $ \ start {align *} w_ {ji} \ end {align *} $ इनलाइन $ ।

यह आपको एक भारित मैट्रिक्स को निर्दिष्ट करने की अनुमति देगा$$ $ इनलाइन $ \ start {align *} M ^ w \ end {align *} $ इनलाइन $ संक्रमण संभावनाएँ:

$$$ इनलाइन $ \ start {align *} M ^ {w} _ {ij} = \ left \ {शुरू करना {मैट्रिक्स} \ frac {w_ {ij}} {\ _ sum_ {j} w_ {ij}} & \ _ toall i, j \ iff e (i, j) \ E में, \\ 0 & \ _ forall i, j \ iff e (i, j) \ notin E. \ end {मैट्रिक्स} \ right। \ end {align *}। $ इनलाइन $

ट्रम्प दुर्घटना से, पहले की तरह संक्रमण बना देगा, लेकिन यह अब उतना ही संभव नहीं है!

एक चौकस पाठक पहले ही सोच चुका है कि इन वज़न को कैसे मापें।

2011 में इसी बात से फेसबुक हैरान था। नए कनेक्शन के निर्माण को अधिकतम करने के लिए दोस्तों के दोस्तों से दोस्तों के लिए एक सिफारिश प्रणाली का निर्माण करना आवश्यक था। और पहला कदम उपयोगकर्ताओं को उनके प्रोफाइल और इंटरैक्शन हिस्ट्री (पसंद, संदेश, संयुक्त फोटो आदि) से जानकारी के बीच कनेक्शन का भारित ग्राफ बनाना था। किसी तरह इंटरनेट पर दोस्ती की शक्ति को मापें।

$$$ $ प्रदर्शन $ $ w_ {ij} = f ^ w (i, j) = e ^ {- \ sum_ {z} {\ xi_z x_ {ij} [z]}}, $ $ $ $ प्रदर्शित

जहाँ$$ $ इनलाइन $ \ start {align *} x_ {ij} \ end {align *} $ इनलाइन $ क्या कोने के गुणों के वेक्टर और उन्हें जोड़ने वाले किनारे हैं, अर्थात्।$$ $ इनलाइन $ \ start {align *} x_ {ij} = f ^ {(i)} \ कप f ^ {(j)} \ कप f ^ {e (ij)} \ अंत {align *} $ इनलाइन $ , और$$ $ इनलाइन $ \ start {align *} \ xi \ end {align *} $ इनलाइन $ क्या वेट का वेक्टर डेटा से सीखा जा सकता है।

यहां, एक प्रशिक्षित पाठक एक रेखीय मॉडल को पहचान लेगा, और एक अप्रस्तुत पाठक इस तथ्य के बारे में सोचेगा कि यह ग्रेडिएंट डिसेंट से निपटने के लिए एक ओपन मशीन लर्निंग कोर्स लेने लायक है, जिसके साथ हम एक वेक्टर में वेट के मूल्यों को सीखेंगे।$$ $ इनलाइन $ x_ {ij} $ इनलाइन $ - वे दिखाएंगे कि कैसे पसंद और संदेश इंटरनेट पर दोस्ती को प्रभावित करते हैं।

हमें यह सब क्यों चाहिए?

इस तथ्य के अलावा कि विचाराधीन दृष्टिकोण हमें बेहतर तरीके से कनेक्शन की भविष्यवाणी करने की अनुमति देता है, हम सफल टीम निर्माण के नियमों को सीख सकते हैं। और पता करें कि भविष्य में क्या देखना है।

हमारे व्यायाम की शर्तों को याद करें। हम अंतराल में सशर्त डेटाशास्‍त्रियों के समूह में सहयोग के विकास (प्रतियोगिताओं में संयुक्त भागीदारी) का निरीक्षण करते हैं$$ $ इनलाइन $ \ start {संरेखित *} (t_0, t_0 ^ \ सितारा) \ अंत {संरेखित}} $ इनलाइन $ (उदाहरण के लिए, एक कैलेंडर माह) और हम अंतराल में टीम निर्माण की भविष्यवाणी करना चाहते हैं$$ $ इनलाइन $ \ start {संरेखित *} (t_1, t_1 ^ \ सितारा) \ अंत {संरेखित}} $ इनलाइन $ (एक और महीना)। प्रतियोगिताओं में भाग लेने के अलावा, हम मंचों पर संचार को पसंद करते हैं, गुठली पसंद करते हैं, और आपको और क्या पसंद है। सभी एकत्रित जानकारी एक मैट्रिक्स में संग्रहीत होती है$$ $ इनलाइन $ X ^ {\ star} \ in \ mathbb {R} ^ {(2k + l) कई बार | E |} $ इनलाइन $ (उसके कॉलम वैक्टर हैं$$ $ इनलाइन $ x_ {ij} $ इनलाइन $ ।$$ $ इनलाइन $ k, l $ इनलाइन $ - कोने और किनारों के गुणों के वैक्टर के आयाम$$ $ इनलाइन $ f ^ {(i)}, f ^ {e (ij)} $ इनलाइन $ , क्रमशः) और ग्राफ$$ $ इनलाइन $ \ start {align *} G \ end {align *} $ इनलाइन $ दो समय के अंतराल के लिए।

आइए मशीन सीखने के लिए डेटा तैयार करें।

प्रत्येक शीर्ष के लिए$$ $ इनलाइन $ \ start {align *} i \ end {align *} $ इनलाइन $ :

1) दोस्तों के कई दोस्तों को परिभाषित करें:

$$$ $ प्रदर्शन $ $ \ गामा ^ {fof} (i) = \ bigcup_ {j \ _ in गामा (i)} \ गामा (जे) - \ गामा (i) $ $ प्रदर्शन $ $

2) और उप-ग्राफ़ का निर्माण$$ $ इनलाइन $ \ start {align *} G ^ {fof} (i) \ end {align *} $ इनलाइन $ दोस्तों और दोस्तों के दोस्तों के साथ संबंध,$$ $ इनलाइन $ \ start {align *} \ forall e (x, y) \ _ में E, e (x, y) \ _ in G ^ {fof} (i) \ iff x, y \ in \ Gamma ^ {fof} (i) \ cup \ Gamma (i) \ end {संरेखित *} $ इनलाइन $

3) कोने के सेट का चयन करें,$$ $ इनलाइन $ \ start {align *} D_i: \ {d_1, ..., d_k \} \ end {संरेखित}} $ इनलाइन $ जिनके साथ हमने संबंध बनाए हैं वे सीखने के लिए हमारे सकारात्मक उदाहरण हैं,

4) सेट से सभी गैर-यादृच्छिक कनेक्शन$$ $ इनलाइन $ \ start {align *} \ overline {D_i} = \ Gamma ^ {fof} (i) - D_i \ end {संरेखित}} $ इनलाइन $ - प्रशिक्षण के लिए ये हमारे नकारात्मक उदाहरण हैं।

हमारा काम वजन के ऐसे वेक्टर का चयन करना है$$ $ इनलाइन $ \ start {align *} \ xi \ end {align *} $ इनलाइन $ जिसमें सेट से सकारात्मक उदाहरण हैं$$ $ इनलाइन $ \ start {align *} D_i \ end {align *} $ इनलाइन $ के सापेक्ष उच्चतर निजीकृत PageRank मान मिलेगा$$ $ इनलाइन $ \ start {align *} i \ end {align *} $ इनलाइन $ नकारात्मक उदाहरणों से।

ऐसा करने के लिए, हम नुकसान फ़ंक्शन को परिभाषित करते हैं, जिसे हम न्यूनतम करेंगे:

$$$$ प्रदर्शन $ $ L = \ sum_ {i} \ sum_ {d \ _ D_i, \ overline {d} \ _ in \ overline {D_i}} h (r _ {\ overline {d}} - r_ / d}) + \ lambda || \ xi || ^ 2, $ $ $ $ प्रदर्शित

जहाँ$$ $ इनलाइन $ h (x) = 0 \ iff x <0; h (x) = x ^ 2 \ iff x \ geqslant 0; $ इनलाइन $ - शर्तों के उल्लंघन के लिए जुर्माना,$$ $ इनलाइन $ \ lambda $ इनलाइन $ - शक्ति$$ $ इनलाइन $ L_2 $ इनलाइन $ वजन को नियमित करना$$ $ इनलाइन $ \ xi $ इनलाइन $ ।$$ $ इनलाइन $ आर $ इनलाइन $ समीकरण के समाधान के साथ एक वेक्टर है$$ $ इनलाइन $ r = M ^ wr $ इनलाइन $ के बारे में$$ $ इनलाइन $ आर $ इनलाइन $ एक शीर्ष के दोस्तों के दोस्तों के उप-ग्राफ के लिए$$ $ इनलाइन $ मैं $ इनलाइन $ ।

एक मज़ेदार विवरण - इस फ़ंक्शन का ग्रेडिएंट पावर विधि द्वारा पेजरैंक के समान गणना की जाती है। विवरण 2014 संस्करण के 17 वें व्याख्यान, स्लाइड 9-27 में हैं।

इस तरह से प्रगति के भाले को मेरे पहले परिचित के समय में cs224w पाठ्यक्रम के साथ देखा गया।

यादृच्छिक घुमक्कड़ पथ और वेक्टर में शीर्ष

और फिर आलस्य की विजय हुई!

यह ज्ञात है कि रेखांकन का सिद्धांत लियोनार्ड यूलर द्वारा आविष्कार किया गया था जब वह कलिनिनग्राद में अब पुलों के बारे में अकल्पनीय समस्या को हल करने से ऊब गया था। कुछ भी नहीं करने के लिए अपने सिर को सुखाने के बजाय, उन्होंने एक गणितीय उपकरण का आविष्कार किया जो उन्हें पहेली को सुलझाने की मौलिक असंभवता साबित करने की अनुमति देता है।

कम्प्यूटेशनल विज्ञान की सर्वश्रेष्ठ परंपराओं में, हम आलसी भी होंगे और अपने आप को एक फ़ंक्शन खोजने का काम पूछेंगे जो हमें नोड्स के एक आयामी प्रतिनिधित्व से दूर जाने और बहुआयामी संपत्ति वैक्टर में जाने की अनुमति देगा।

यहाँ हम शब्द के आधुनिक अर्थ में ग्राफ एम्बेडिंग से परिचित हैं।

औपचारिक रूप से, हम चाहते हैं:

1) एक एनकोडर (एक ईएनसी अनुरूपता फ़ंक्शन) को परिभाषित करें जो एक नोड परिवर्तन को परिभाषित करता है$$ $ इनलाइन $ यू $ इनलाइन $ वेक्टर में$$ $ इनलाइन $ z_u $ इनलाइन $ );
2) नोड्स की समानता का कार्य निर्धारित करें (ग्राफ में निकटता का एक उपाय, जिसे हम एनकोडर के इनपुट पर लागू करेंगे);
3) एनकोडर मापदंडों का अनुकूलन करें ताकि:

$$$ $ प्रदर्शन $ $ समानता (यू, वी) \ लगभग z_ {v} ^ {T} z_v $ $ प्रदर्शन $ $

हम यह सुनिश्चित करने का प्रयास करते हैं कि ग्राफ में बारीकी से स्थित वेक्टर वेक्टर मैपिंग में एक करीबी प्रतिनिधित्व प्राप्त करते हैं। दूसरे शब्दों में, ताकि प्राप्त किए गए दो वैक्टरों के बीच का कोण न्यूनतम हो।

महान, लेकिन इसे कैसे निर्धारित किया जाए, ग्राफ में यह निकटता?

उदाहरण के लिए, हम मानते हैं कि पसली का वजन निकटता का एक अच्छा उपाय है और लगभग दो नोड्स के एम्बेडिंग के लिए स्केलर उत्पाद के बराबर माना जा सकता है। इस मामले के लिए नुकसान समारोह फार्म ले जाएगा:

$$$$ प्रदर्शन $ $ L = \ योग _ {(u, v) \ _ में \ _ बार V} || z_ {u} ^ {T} z_v - A_ {u, v} || ^ 2, $ $ $ $ $ प्रदर्शित

यह मैट्रिक्स को खोजने के लिए बना हुआ है (उदाहरण के लिए, ढाल वंश)$$ $ इनलाइन $ Z \ in \ mathbb {R} ^ {d \ टाइम्स | V |} $ इनलाइन $ जो कम से कम हो$$ $ इनलाइन $ एल $ इनलाइन $ ।

पर्यावरण का निर्धारण करने के लिए एक वैकल्पिक दृष्टिकोण है।$$ $ इनलाइन $ एन (v) $ इनलाइन $ शिखर सम्मेलन के लिए कई पड़ोसियों की तुलना में व्यापक है।

यह हमें ग्राफ के आसपास चलने में मदद करेगा। इस दृष्टिकोण का उपयोग करने वाली पहली परियोजना दीपवाक है । विधि का सार यह है कि हम प्रत्येक शीर्ष से यादृच्छिक रूप से ग्राफ़ के चारों ओर चलने के लिए एक ट्रैंप शुरू करेंगे$$ $ इनलाइन $ v $ इनलाइन $ , और word2vec में चलने के दौरान चोटियों की निश्चित लंबाई के छोटे दृश्यों को फ़ीड करें।

यहाँ अंतर्ज्ञान यह है कि ग्राफ के कोने पर जाने की प्रायिकता वितरण - एक शक्ति नियम - मानव भाषाओं में शब्दों की उपस्थिति की संभावना वितरण के समान है। और जब से शब्द 2vec शब्दों के लिए काम करता है, तब ग्राफ के लिए यह कर सकता है। हमने कोशिश की - यह काम किया!

दीपवाक में, एक ट्रम्प एक प्रथम-क्रम मार्कोव प्रक्रिया को लागू करता है - प्रत्येक शीर्ष से हम पड़ोसी के पास जाते हैं, एक भारित आसन्न मैट्रिक्स से संभावनाओं के अनुसार$$ $ इनलाइन $ एम $ इनलाइन $ (या इसके डेरिवेटिव, जैसे$$ $ इनलाइन $ एम ^ डब्ल्यू $ इनलाइन $ )। जहां हम शीर्ष पर आए, अगले चरण की पसंद को प्रभावित नहीं करता है।

चलने को लागू करने के लिए, आपको एक छद्म यादृच्छिक संख्या जनरेटर और बीजगणित की थोड़ी आवश्यकता होगी। यह अपने इच्छित उद्देश्य के लिए उद्धरणों के लिए ब्लॉक का उपयोग करने का समय है।

“कोई भी, जो पीढ़ी के अंकगणितीय तरीकों से सहमत है, ज़ाहिर है, पापी है। जैसा कि बार-बार दिखाया गया है, एक यादृच्छिक संख्या जैसी कोई चीज नहीं है - ऐसी संख्याएं बनाने के लिए केवल विधियां हैं, और एक सख्त अंकगणितीय प्रक्रिया, निश्चित रूप से, ऐसी कोई विधि नहीं है ... हम केवल संख्या बनाने के लिए व्यंजनों से निपटते हैं ... "

- जॉन वॉन न्यूमैन

यह एक धर्मी जीवन के लिए "ब्लैक एंड व्हाइट शोर" एल्बम को खोजने के लिए बिक्री के लिए प्रयास करने के लिए रहता है - 1995 में जॉर्ज मार्साग्लिया ने सीडी पर एक बाइट्स की एक सरणी लिखी जो रैप कलाकार को बजाने के दौरान एम्पलीफायर से शोर को अंकीयकरण करके प्राप्त की और उसी के अनुसार नाम दिया।

विधि का विकास नोड 2vec है , जिसमें दूसरे क्रम के मार्कोव प्रक्रिया को लागू किया जाता है - हम देखते हैं कि यह कहां से आया है, और यह अगले चरण की दिशा चुनने की संभावना को प्रभावित करता है। आइए देखें कि यह कैसे काम करता है।

मान लीजिए कि हम ऊपर से ग्राफ के चारों ओर घूमना शुरू करते हैं$$ $ इनलाइन $ यू $ इनलाइन $ ऊपर से सटे हुए$$ $ इनलाइन $ s_1 $ इनलाइन $ कोने$$ $ इनलाइन $ s_2 $ इनलाइन $ और$$ $ इनलाइन $ w $ इनलाइन $ - दो चरणों में, और$$ $ इनलाइन $ s_3 $ इनलाइन $ - तीन में। प्रत्येक चरण के बाद, हम तीन संभावित क्रियाओं में से एक का प्रदर्शन कर सकते हैं: 1) के करीब लौटें$$ $ इनलाइन $ यू $ इनलाइन $ ; 2) उसी दूरी से चोटियों का पता लगाएं$$ $ इनलाइन $ यू $ इनलाइन $ , जैसा कि अब हम कर रहे हैं; ३) दूर हटो$$ $ इनलाइन $ यू $ इनलाइन $ ।

यह रणनीति दो मापदंडों का उपयोग करके कार्यान्वित की जाती है:
$$$ इनलाइन $ पी $ इनलाइन $ - पिछले शीर्ष पर लौटने की संभावना निर्धारित करता है;
$$$ इनलाइन $ q $ इनलाइन $ - चौड़ाई में खोज और गहराई में खोज के बीच संतुलन स्थापित करता है।

ये पैरामीटर्स इस प्रकार के अस्वाभाविक परिवर्तन की संभावनाओं का निर्धारण करते हैं:

मान लीजिए कि हम शीर्ष पर हैं$$ $ इनलाइन $ w $ इनलाइन $ और ऊपर से इसमें आ गया$$ $ इनलाइन $ s_1 $ इनलाइन $ । रिब के लिए$$ $ इनलाइन $ ई (w, s_1) $ इनलाइन $ हम वजन (असंभावित संभावना) सौंपेंगे$$ $ इनलाइन $ 1 / p $ इनलाइन $ । रिब के लिए$$ $ इनलाइन $ ई (w, s_2) $ इनलाइन $ -$$ $ इनलाइन $ 1 $ इनलाइन $ (के रूप में सभी अन्य किनारों से कोने तक जाने के लिए समतुल्य है$$ $ इनलाइन $ यू $ इनलाइन $ )। से दूर जाने के लिए$$ $ इनलाइन $ यू $ इनलाइन $ रिब्स$$ $ इनलाइन $ ई (w, s_3) $ इनलाइन $ -$$ $ इनलाइन $ 1 / q $ इनलाइन $ ।

फिर हम संभावनाओं को सामान्य करते हैं (ताकि योग 1 के बराबर हो), और अगला कदम उठाएं।

हम दौरा किए गए चोटियों के अनुक्रम में रुचि रखते हैं - हम इसे word2vec पर भेजेंगे ( यह लेख आपको इससे निपटने में मदद करेगा, या उंगलियों पर दीप लर्निंग कोर्स से 8 व्याख्यान)। ट्रम्प के लिए रणनीतियों का चयन, विशिष्ट समस्याओं को हल करने के लिए इष्टतम सक्रिय अनुसंधान का एक क्षेत्र है। उदाहरण के लिए, नोड 2vec, जिसकी हमने समीक्षा की, चोटियों के वर्गीकरण में एक चैंपियन है (उदाहरण के लिए, दवाओं की विषाक्तता का निर्धारण, या एक सामाजिक नेटवर्क के सदस्य की सेक्स / उम्र / दौड़)।

हम ट्रैम्प के मार्ग में चोटियों की उपस्थिति की संभावना को खो देंगे, हानि कार्य:

$$$ $ $ $ $ L = \ sum_ {u \ _ in}} \ sum_ {v \ N_ {R} (u)} -लॉग (P (v | z_u)) $$ प्रदर्शन $$

अपने स्पष्ट रूप में, एक महंगा कम्प्यूटेशनल बोझ है

$$$ $ $ $ $ L = \ sum_ {u \ _ in}} \ sum_ {v \ N_ {R} (u)} -लॉग (\ frac {e ^ {z_ {u} ^ {T} z_v}} { \ sum_ {n \ _ in V} e ^ {z_ {u} ^ {T} z_n}}), $ $ $ $ प्रदर्शित करें

जो, एक अस्थायी द्वारा, नकारात्मक नमूने द्वारा हल किया जाता है, क्योंकि

$$$ $ प्रदर्शन $ $ लॉग (\ frac {e ^ {z_ {u} ^ {T} z_v}} {\ sum_ {n \ _ V} e ^ {z_ {u} ^ {T} z_n}}) लगभग लॉग (\ sigma (z_ {u} ^ {T} z_v)) - \ sum_ {i = 1} ^ {k} लॉग (\ sigma (z_ {u} ^ {T} z_ {n_i}), \\ जहाँ \ _, \ _, n_i \ sim P_V, \ sigma (x) = \ frac {1} {1 + e ^ {- x}}। $ $ $ $ प्रदर्शित होते हैं।

इसलिए, हमने यह पता लगाया कि वर्टीकल का सदिश प्रतिनिधित्व कैसे प्राप्त किया जाए। बात टोपी की है!

पसलियों के लिए एम्बेडिंग कैसे तैयार करें:

हमें एक ऑपरेटर को परिभाषित करने की आवश्यकता है जो किसी भी जोड़ी के लिए अनुमति देता है$$ $ इनलाइन $ यू $ इनलाइन $ और$$ $ इनलाइन $ v $ इनलाइन $ वेक्टर प्रतिनिधित्व बनाएँ$$ $ इनलाइन $ z _ {(u, v)} = जी (z_u, z_v) $ इनलाइन $ भले ही वे ग्राफ पर जुड़े हों। ऐसा ऑपरेटर हो सकता है:

a) अंकगणित माध्य:$$ $ इनलाइन $ [z_u \ oplus z_v] _i = \ frac {z_u (i) + z_v (i)} {2} $ इनलाइन $ ;
ख) हाडामर्ड का काम:$$ $ इनलाइन $ [z_u \ odot z_v] _i = z_u (i) * z_v (i) $ इनलाइन $ ;
ग) भारित L1 मानदंड:$$ $ इनलाइन $ || z_u - z_v || _ {\ overline {1} i = = | z_u (i) - z_v (i) | $ इनलाइन $ ;
घ) भारित L2 दर:$$ $ इनलाइन $ || z_u - z_v || _ {\ overline {2} i} = | z_u (i) - z_v (i) | ^ 2 $ इनलाइन $ ।

प्रयोगों में, हैडमार्ड का काम सबसे तेजी से व्यवहार करता है।

बस के मामले में, मुफ्त लंच प्रमेय याद रखें:

कोई एल्गोरिथ्म सार्वभौमिक नहीं है - यह कई तरीकों की जाँच करने के लायक है।

नोड 2vec का विकास ओह्मनेट प्रोजेक्ट है, जो आपको कई ग्राफ को एक पदानुक्रम में संयोजित करने और पदानुक्रम के विभिन्न स्तरों के लिए वर्टेक्स एम्बेडिंग बनाने की अनुमति देता है। यह मूल रूप से विभिन्न अंगों में प्रोटीन के बीच बांड को मॉडल करने के लिए विकसित किया गया था (और वे स्थान के आधार पर अलग-अलग व्यवहार करते हैं)।

एक चतुर पाठक संगठनात्मक संरचना और व्यावसायिक प्रक्रियाओं के साथ समानताएं देखेंगे।

और हम - हम आईटी भर्ती के क्षेत्र से एक उदाहरण पर लौटेंगे - उन लोगों का चयन जो पहले से मौजूद टीम के लिए सबसे उपयुक्त हैं। इससे पहले, हमने बातचीत के इतिहास से प्राप्त सशर्त डेटाशास्‍त्रियों के संबंधों के एकतरफा रेखांकन पर विचार किया (वर्टेक्स के अनिमॉडल ग्राफ और कनेक्शन में - एक ही प्रकार का)। हकीकत में, एक व्यक्ति को शामिल किए जाने वाले सामाजिक दायरे की संख्या एक से अधिक हो सकती है।

मान लीजिए, प्रतियोगिताओं में संयुक्त भागीदारी के इतिहास के अलावा, हमने इस बारे में भी जानकारी एकत्र की है कि कैसे हमारे आरामदायक चैट में डेटाैसेंटिस का संचार होता है। अब हमारे पास पहले से ही कनेक्शन के दो ग्राफ़ हैं, और कई संरचनाओं से एम्बेडिंग बनाने की समस्या को हल करने के लिए ओह्मनेट सही है।

अब - उथले एनकोडर के आधार पर तरीकों की कमियों के बारे में - word2vec के अंदर केवल एक छिपी हुई परत है, जिसके वजन एन्कोडिंग को एन्कोड करते हैं। आउटपुट पर, हमें एक शीर्ष-वेक्टर पत्राचार तालिका मिलती है। ऐसे सभी दृष्टिकोणों की निम्नलिखित सीमाएँ हैं:

• प्रत्येक शीर्ष को एक अद्वितीय वेक्टर द्वारा एन्कोड किया गया है और मॉडल मापदंडों को साझा नहीं करता है;
• हम केवल उन शीर्ष रेखाओं को एन्कोड कर सकते हैं जो मॉडल ने प्रशिक्षण के दौरान देखा था - हम नए कोने के लिए कुछ भी नहीं कर सकते (सिवाय एनकोडर को फिर से कैसे करें) को छोड़कर;
• वर्टेक्स संपत्ति वैक्टर को किसी भी तरह से ध्यान में नहीं रखा जाता है।

ग्राफ कन्वेन्शनल नेटवर्क संकेतित कमियों से मुक्त हैं। हम डेक्कन के पास पहुंच गए!

हमारे दिन हर किसी और हर किसी के लिए एक यादृच्छिक ट्रम्प हैं

ट्रम्प के बारे में, मैं अपने पहले मास्टर की डिग्री लिखने और 2003 में इसका बचाव करने के लिए भाग्यशाली था, लेकिन गहन प्रशिक्षण के साथ मुझे यह पता लगाने के लिए शास्त्रीय तरीके से जाना पड़ा कि हुड के नीचे क्या था। और यह वहाँ अजीब है।

सबसे पहले, आइए देखें कि गहरी सीखने के मानक तरीके - ग्राफ़ के लायक क्यों नहीं हैं।

मायने रखता है आपके लिए बिल्लियाँ नहीं हैं!

गहरी शिक्षण उपकरण (बहुपरत, दृढ़, और आवर्तक नेटवर्क) का आधुनिक सेट काफी सरल डेटा - अनुक्रम और लैटिस पर समस्याओं को हल करने के लिए अनुकूलित है। एक ग्राफ एक अधिक जटिल संरचना है। समस्याओं में से एक जो हमें आसन्न मैट्रिक्स को लेने और तंत्रिका नेटवर्क पर भेजने से रोकती है वह है समरूपता ।

हमारे खिलौने के कॉलम में$$ $ इनलाइन $ जी $ इनलाइन $ वर्टिस से मिलकर$$ $ इनलाइन $ \ {A, B, C, D \} $ इनलाइन $ , एक आसन्न मैट्रिक्स का निर्माण करने के लिए$$ $ इनलाइन $ एक $ इनलाइन $ , हमने एंड-टू-एंड नंबरिंग का सुझाव दिया$$ $ इनलाइन $ \ {1,2,3,4 \} $ इनलाइन $ । यह देखना आसान है कि हम भिन्न संख्याओं को उदाहरण के लिए अलग कर सकते हैं$$ $ इनलाइन $ \ {1,3,2,4 \} $ इनलाइन $ , या$$ $ इनलाइन $ \ {4,1,3,2 \} $ इनलाइन $ - हर बार एक ही ग्राफ का एक नया आसन्न मैट्रिक्स प्राप्त करना।

$$$ इनलाइन $ \ start {align *} A = \ left [\ start {मैट्रिक्स} 0 & 1 & 3 & 0 \\ 1 & 0 & 2 & 1 & \ _ 3 और 2 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \ end {मैट्रिक्स} \ सही], \, A ^ {\ {1,3,2,4 \}} = \ छोड़ दिया [\ start {मैट्रिक्स} 0 और 3 और 1 & 0 \\ 3 & 0 & 2 & 0 \\ 1 & 2 और 0 & 1 \\ 0 & 0 & 1 & 0 \ end {मैट्रिक्स} \ सही], \, A ^ {\ {4,1,3,2 \}} = \ बाएँ [\ _ {मैट्रिक्स} 0 और 1 & 2 & 1 \\ 1 & 0 & 0 & 0 \\ 2 & 0 & 0 & 3 & \ _ 1 & 0 & 3 & 0 \ अंत {मैट्रिक्स} \ सही]। \ अंत {संरेखित *} $ इनलाइन $

जवानों के मामले में, हमारे नेटवर्क को पंक्तियों और स्तंभों के सभी संभावित क्रमों के लिए उन्हें पहचानना सीखना होगा - यह एक और समस्या है। एक अभ्यास के रूप में, नीचे की छवि में अंक की संख्या को बदलने का प्रयास करें ताकि जब आप उन्हें श्रृंखला में जोड़ते हैं, तो आपको एक बिल्ली मिल जाए।

साधारण तंत्रिका नेटवर्क के साथ रेखांकन के लिए अगली समस्या मानक इनपुट आयाम है। जब हम छवियों के साथ काम करते हैं, तो हम हमेशा नेटवर्क इनपुट को भेजने के लिए छवि के आकार को सामान्य करते हैं - यह एक निश्चित आकार है। ऐसे ग्राफ़ ग्राफ़ के साथ काम नहीं करेंगे - कोने की संख्या मनमानी हो सकती है - बिना सूचना खोए किसी दिए गए आयाम से कनेक्टिविटी मैट्रिक्स को निचोड़ना एक और चुनौती है।

समाधान - हम नए आर्किटेक्चर का निर्माण करेंगे, जो रेखांकन की संरचना से प्रेरित होंगे।

ऐसा करने के लिए, हम एक सरल दो-चरणीय रणनीति का उपयोग करते हैं:

1. प्रत्येक शीर्ष के लिए, हम एक ट्रम्प का उपयोग करके एक कम्प्यूटेशनल ग्राफ का निर्माण करते हैं;
2. हम पड़ोसियों के बारे में जानकारी एकत्र करते हैं और बदलते हैं।

स्मरण करो कि हम वैक्टर में कोने के गुणों को संग्रहीत करते हैं$$ $ इनलाइन $ f ^ {(u)} $ इनलाइन $ - मैट्रिक्स कॉलम$$ $ इनलाइन $ X \ in \ mathbb {R} ^ {k \ टाइम्स | V |} $ इनलाइन $ और हमारा कार्य प्रत्येक शीर्ष के लिए है$$ $ इनलाइन $ यू $ इनलाइन $ पड़ोसी कोने के गुण एकत्र करें$$ $ इनलाइन $ f ^ {(v (एन (यू) में))} $ इनलाइन $ एम्बेडिंग वैक्टर पाने के लिए$$ $ इनलाइन $ z_ {u} $ इनलाइन $ । एक कम्प्यूटेशनल ग्राफ मनमाना गहराई का हो सकता है। दो-परत विकल्प पर विचार करें।

शून्य परत कोने के गुण हैं, पहला एक फ़ंक्शन (प्रश्न चिह्न द्वारा इंगित) का उपयोग करके एक मध्यवर्ती एकत्रीकरण है, दूसरा अंतिम एकत्रीकरण है, जो हमारे लिए ब्याज के एम्बेडिंग वैक्टर का उत्पादन करता है।

और बक्सों में क्या है?

साधारण मामले में , न्यूरॉन्स और गैर-रैखिकता की एक परत:

$$$$ प्रदर्शन $$ h ^ 0_v = x_v (= f ^ {(v)}); \\ h ^ k_v = \ sigma (W_k \ sum_ {u \ _ in N (v)} \ frac {h ^ {k-1} _v} {| N (v) |} + B_k h ^ [k-1} | _v), \ forall k \ _ in {{1, ..., K \}; \\ z_v = h ^ K_v, $$ प्रदर्शन $ $

जहाँ$$ $ इनलाइन $ W_k $ इनलाइन $ और$$ $ इनलाइन $ B_k $ इनलाइन $ - मॉडल का वजन जो हम क्रमिक वंश द्वारा सीखेंगे, माना नुकसान कार्यों में से एक को लागू करना, और$$ $ इनलाइन $ \ सिग्मा $ इनलाइन $ - गैर-समानता, उदाहरण के लिए RELU:$$ $ इनलाइन $ \ सिग्मा (x) = अधिकतम (0, x) $ इनलाइन $ ।

और यहाँ हम खुद को एक चौराहे पर पाते हैं - हाथ में काम के आधार पर, हम यह कर सकते हैं:

• एक शिक्षक के बिना अध्ययन करने के लिए और पहले से विचार किए गए नुकसान कार्यों में से किसी का लाभ उठाएं - ट्रैंप, या किनारों का वजन। परिणामस्वरूप वजन को अनुकूलित किया जाएगा ताकि समान कोने के वैक्टर को कॉम्पैक्ट रूप से रखा जाए;
• एक शिक्षक के साथ प्रशिक्षण शुरू करें, उदाहरण के लिए, वर्गीकरण समस्या को हल करने के लिए, यह सोचकर कि क्या दवा विषाक्त होगी।

द्विआधारी वर्गीकरण समस्या के लिए, नुकसान फ़ंक्शन रूप लेता है:

$$$ $ $ $ $ L = \ sum_ {v \ _ V} y_v लॉग (\ sigma (z_v ^ T \ थीटा)) + ((1-y_v) लॉग (1- \ सिग्मा (z_v ^ \ _ta)), $ $ प्रदर्शन $ $

जहाँ$$ $ इनलाइन $ y_v $ इनलाइन $ - वर्टेक्स क्लास$$ $ इनलाइन $ v $ इनलाइन $ ।$$ $ इनलाइन $ \ थीटा $ इनलाइन $ वजन का वेक्टर है, और$$ $ इनलाइन $ \ सिग्मा $ इनलाइन $ - अशुद्धता, उदाहरण के लिए एक सिग्मोइड:$$ $ इनलाइन $ \ सिग्मा (x) = \ frac {1} {1 + e ^ {- x}} $ इनलाइन $ ।

यहां, एक प्रशिक्षित पाठक क्रॉस-एन्ट्रापी और लॉजिस्टिक रिग्रेशन को पहचान लेगा, जबकि एक अप्रस्तुत पाठक वर्गीकरण कार्य के साथ सहज महसूस करने के लिए एक ओपन मशीन लर्निंग कोर्स लेने के बारे में सोचेगा, इसे हल करने के लिए सरल , और अधिक उन्नत एल्गोरिदम ( ग्रेडिएंट बूस्टिंग सहित)।

और हम आगे बढ़ेंगे और विचार करेंगे कि कैसे Decagon के ग्राफिंगर , काम करता है।

प्रत्येक शीर्ष के लिए$$ $ इनलाइन $ v $ इनलाइन $ हम पड़ोसियों से जानकारी एकत्र करेंगे$$ $ इनलाइन $ u \ N (v) $ इनलाइन $ और खुद को।

$$$$ प्रदर्शन $ $ h ^ k_v = \ sigma ([W_k \ cdot AGG (\ {h ^ {k-1} _u, \ forall u \ n (v) \}), B_k h {k-1} _v]), $ $ प्रदर्शन $ $

जहाँ$$ $ इनलाइन $ एजीजी $ इनलाइन $ - एकत्रीकरण समारोह का एक सामान्यीकृत पदनाम - सबसे महत्वपूर्ण - विभेदी।

एवरेजिंग: पड़ोसियों से एक भारित औसत लें

$$$ $ प्रदर्शन $ $ AGG = \ sum_ {u \ N (v)} \ frac {h ^ {k-1} _u} {| N (v) |}। $ $ $ $ प्रदर्शन

पूलिंग: तत्व-वार औसत / अधिकतम मूल्य

$$$ $ प्रदर्शन $ $ AGG = \ gamma (\ {Qh ^ {k-1} _u, \ forall u \ N (v) \}) में। $ $ $ $ प्रदर्शन।

LSTM: पर्यावरण को हिलाएं (मिलाएं नहीं!) और LSTM में चलाएं

$$$$ प्रदर्शन $ $ AGG = LSTM ([h ^ {k-1} _u, \ forall u \ in \ pi (N (v))])। $$ प्रदर्शन $$

Pinterest, , PinSAGE .

LSTM ( ). IT-.

:

• : , — , .
• , : / , — .

, — . , . , , , . (/) , , , — — , 30 .

.

— (multi-label node
classification task) — . — . () ( — — 42% ). GraphSAGE, , — .

!

, — , , . , .

- , Decagon. , -, -, , -, — ri . . - 964 ( ) .

— , -, -.

,

$$

$$h^k_v = \sigma(\sum_rW^{k-1}_r(\sum_{u \in N_r(v)} \frac{h^{k-1}_u}{\sqrt{|N_r(v)||N_r(u)|}}+\frac{h^{k-1}_v}{|N_r(v)|})),$$

जहाँ$$σ$\sigma$ — , RELU. , Decagon — . , , GraphSAGE. , .

, .

— , . -.$$(u,r,v)$(u,r,v)$ , :

$$g(u,r,v)={zTuDriRDrizju,v−;zTuMrzvu,v−,.$\begin{align*}g(u,r,v) = \left\{ \begin{matrix} z^T_uD_{r_i}RD_{r_i}z_j & u,v - ; \\ z^T_uM_rz_v & u,v - \, \, , \,\, \, . \end{matrix} \right.\end{align*}$

, :

$$

$$p^{uv}_{r} = p((u,r,v) \in E) = \sigma (g(u, r, v)), \sigma(x) = \frac{1}{1 + e^{-x}}.$$

, (end-to-end) -, : (i)$$Wr$W_r$ — , (ii)$$Mr$M_r$ — - -, (iii)$$R$R$ — , (iv)$$Dri$D_{r_i}$ — .

— - .

— .

— , , : 1) — — ; 2) " , , , " — - . , , , .

— — .

, ( ) , . , , GenBank 1 , , - — , . — , - ( ) , SNAP .

.

Neo4j , (property graph).

, . , , — (i) -, (ii) , (iii) , — — . .

— :

इसके अलावा, उद्योग में Neo4j का योगदान घोषणात्मक Cypher भाषा बनाने में है , जो गुणों के साथ एक ग्राफ़ मॉडल लागू करता है और निम्न डेटा प्रकारों के साथ SQL के समान रूप में संचालित होता है: कोने, संबंध, शब्दकोष, सूचियाँ, पूर्णांक, फ़्लोटिंग पॉइंट, और बाइनरी नंबर, और लाइन। एक उदाहरण क्वेरी जिसमें निकोल किडमैन की फिल्मों की सूची मिलती है:

MATCH (nicole:Actor {name: 'Nicole Kidman'})-[:ACTED_IN]->(movie:Movie) WHERE movie.year < $yearParameter RETURN movie 

बैसाखी का उपयोग करते हुए , Neo4j को मेमोरी में काम करने के लिए बनाया जा सकता है।

यह Gephi को भी ध्यान देने योग्य है - एक विमान पर रेखांकन की कल्पना और बिछाने के लिए एक सुविधाजनक उपकरण - व्यक्तिगत रूप से परीक्षण से पहला नेटवर्क विश्लेषण उपकरण। एक खिंचाव के साथ, हम यह मान सकते हैं कि गेफि में कोने और किनारों के गुणों के साथ एक ग्राफ को लागू करना संभव है, हालांकि इसके साथ काम करना बहुत सुविधाजनक नहीं होगा, और विश्लेषण के लिए एल्गोरिदम का सेट सीमित है। यह पैकेज के गुणों से अलग नहीं होता है - मेरे लिए यह विज़ुअलाइज़ेशन टूल्स के बीच पहले स्थान पर है। आंतरिक GEXF भंडारण प्रारूप में महारत हासिल करके , आप प्रभावशाली चित्र बना सकते हैं। यह वेब पर आसानी से निर्यात करने की क्षमता को आकर्षित करता है, साथ ही साथ समय में कोने और किनारों के लिए गुण सेट करने की क्षमता और इसके परिणामस्वरूप जटिल एनिमेशन प्राप्त करता है - उसने बिक्री डेटा से सेल्समैन की यात्रा के लिए मार्गों का निर्माण किया। पैकेज के मानक भाग - कोने के निर्देशांक द्वारा मानचित्र पर रेखांकन के लेआउट के लिए सभी धन्यवाद।

अब मैं अधिकांश अनुसंधान विश्लेषणात्मक रूप से आयोजित करता हूं, मैं अंत में चित्र खींचता हूं।

जटिल रूप से जुड़े सिस्टम में डेटा को संसाधित करने के लिए टूल और तरीकों की मेरी खोज जारी है। तीन साल पहले मुझे मल्टीमॉडल रेखांकन के साथ काम करने का हल मिला। Jure Leskovek की SNAP लाइब्रेरी एक ऐसा उपकरण है जिसे उन्होंने अपने लिए विकसित किया है और पहले से ही बहुत सारी चीजों को मापा है। मैं Snap.py का उपयोग करता हूं - पायथन के लिए संस्करण (C ++ में कार्यान्वित SNAP फ़ंक्शन के लिए प्रॉक्सी) और लगभग तीन सौ उपलब्ध संचालन का एक सेट मेरे लिए ज्यादातर मामलों में पर्याप्त है।

हाल ही में, Marinka Zhitnik ने MAMBO - मल्टीमॉडल नेटवर्क के साथ काम करने के लिए टूल्स (इनसाइड - एसएनएपी) और ज्यूपिटर नोटबुक की श्रृंखला के रूप में एक ट्यूटोरियल को आनुवंशिक म्यूटेशन के एक अनुकरणीय विश्लेषण के साथ जारी किया।

अंत में, वहाँ एसएपी हाना ग्राफ है - वहाँ एमएल, SQL, OpenCypher - सब कुछ अपने दिल की इच्छाओं के अंदर।

एसएपी हाना के पक्ष में, तथ्य यह है कि खुदाई से ईआरपी से अच्छी तरह से संरचित लेनदेन डेटा की संभावना है, जबकि शुद्ध डेटा बहुत अधिक है। एक और प्लस - दिए गए पैटर्न द्वारा उप-ग्राफ़ खोजने के लिए शक्तिशाली उपकरण - एक उपयोगी और कठिन कार्य, जिसके कार्यान्वयन अन्य पैकेजों में विशेष कार्यक्रमों से नहीं मिले और उनका उपयोग नहीं किया गया। डेवलपर के लिए एक मुफ्त लाइसेंस 1 जीबी डेटाबेस प्रदान करता है - बस बड़े पर्याप्त नेटवर्क के साथ खेलने के लिए पर्याप्त है। एक अजीब कॉल - बॉक्स के बाहर विश्लेषणात्मक एल्गोरिदम का एक सेट - छोटा है, पेजरैंक को स्वतंत्र रूप से लागू करने की आवश्यकता होगी। ऐसा करने के लिए, आपको ग्राफ़िक्सस्क्रिप्ट , एक नई प्रोग्रामिंग भाषा को मास्टर करने की आवश्यकता होगी, लेकिन यह एक ट्रिफ़ल है। जैसा कि मेरे रोइंग स्लैलम ट्रेनर ने कहा, मास्टर के लिए - यह धूल है!

अब उनके बारे में ग्राफ़ बनाने के लिए डेटा कहाँ से मिलेगा। कुछ विचार:

• यूनिवर्सिटी पब्लिक रिपोजिटरी: स्टैनफोर्ड - जनरल और बायोमेडिकल , कोलोराडो ;
• संगठनात्मक संरचना और जोखिम रजिस्टर के साथ परियोजना योजना को मिलाएं;
• उत्पाद संरचना, प्रौद्योगिकी और उपयोगकर्ता की इच्छाओं के बीच संबंध को पहचानें;
• एक टीम में एक समाजशास्त्रीय अध्ययन का संचालन करना;
• अपने खुद के कुछ के साथ आओ, पिछले साल के cs224w पाठ्यक्रम परियोजनाओं से प्रेरित।

डरना क्या?

हम कह सकते हैं कि यहां इस पार्टी से जुड़े जोखिमों के बारे में अंतिम चेतावनी होगी।

जैसा कि आप जानते हैं, देवियों और सज्जनों, कार्यक्रम का उद्देश्य एक बहुत ही उत्पादक और उदारता से वित्त पोषित अनुसंधान समूह के मामले में सबसे आगे है। यह लेनिनग्राद की तरह है, केवल आधुनिक गणित के बारे में। संभावित दुष्प्रभाव:

1. धूर्त-क्रुएगर , एक नौसिखिया और उत्कृष्टता के पठार के बिना संशोधित। Leskovek को पकड़ने की कोशिश करो।
2. समुद्र के द्वारा एक प्रांत में ऊब। पाठ्यक्रम में 400 लोगों में से जिन्हें तंत्र दिया गया था, उन्होंने मुझे एक परियोजना लिखी, और मेरे दूसरे मास्टर कार्यक्रम के दौरान पहले सत्र में परीक्षा पास की, गिनती डेढ़ हो गई। अपने अनुसंधान गतिविधियों में शिक्षक प्रतिरूपकता और केंद्रीयता के स्तर पर बने हुए हैं। अजगर और डेटा के बारे में mitaps पर भी दुख की बात है। सामान्य तौर पर, यदि आप नहीं जानते कि अपना मनोरंजन कैसे किया जाए, तो मैंने आपको चेतावनी दी।
3. अंग्रेजी भाषण में एक स्लाव लहजे में गर्व।

प्लेबैक मेमो

हाय, प्रजननकर्ता!

जुरा लेसकोवेक ने हमें जो रोमांच दिया है, उसमें आपको खाली समय चाहिए। पाठ्यक्रम में 20 व्याख्यान, चार होमवर्क शामिल हैं, जिनमें से प्रत्येक में लगभग 20 घंटे आवंटित करने की सिफारिश की गई है, साहित्य की सिफारिश की गई है, साथ ही अतिरिक्त सामग्रियों की एक व्यापक सूची है जो कि चर्चा किए गए किसी भी विषय में प्रगति के मामले में मामलों की स्थिति का पहला प्रभाव बनाने के लिए संभव होगा।

कार्यों को पूरा करने के लिए, एसएनएपी लाइब्रेरी का उपयोग करने की अत्यधिक अनुशंसा की जाती है (एक अर्थ में, पूरे पाठ्यक्रम को इसकी क्षमताओं का अवलोकन माना जा सकता है)।

इसके अलावा, आप अपनी खुद की परियोजना को लागू करने या अपने पसंद के विषय पर एक ट्यूटोरियल लिखने की कोशिश कर सकते हैं।

मुझे लगता है कि ग्राफ सिद्धांत में डूबने के बाद, पेड़ों के बारे में सवाल अब डरावना नहीं होगा। हालांकि, यह सिर्फ एक शौकिया की राय है जिसने अपने जीवन में कभी भी एक डेवलपर की स्थिति नहीं ली है जिसका साक्षात्कार नहीं हुआ है।