ओलंपियाड समस्याओं में गतिशील प्रोग्रामिंग

नमस्ते!

हाल ही में मैंने टिमस ऑनलाइन जज संग्रह से समस्याओं को हल किया और गतिशील प्रोग्रामिंग कार्यों नामक एक अनुभाग में आया। इस प्रकार का कार्य मेरे लिए विशेष रुचि का है, क्योंकि अक्सर यह दृष्टिकोण समाधान की गति और लालित्य सुनिश्चित करता है। गतिशील प्रोग्रामिंग क्या है?

डायनेमिक प्रोग्रामिंग समस्याओं को हल करने के लिए एक दृष्टिकोण है जिसमें उप-प्रकारों में एक विभाजन होता है जो मूल के साथ तुलना में "सरल" होता है। "गतिशील" शब्द "आगमनात्मक" के करीब है: यह माना जाता है कि उत्तर कुछ अर्थ के लिए जाना जाता है $$$k$ , और मैं इसका जवाब ढूंढना चाहता हूं $$$k + 1$ । गणित में, यह एक प्रेरक संक्रमण कहा जाता है, और गतिशील प्रोग्रामिंग का मुख्य विचार है।

सरल उदाहरण

सबसे हड़ताली और सांकेतिक कार्य कंप्यूटिंग का कार्य है $$$एन$ फाइबोनैचि अनुक्रम की संख्या। यह ज्ञात है कि अनुक्रम में निम्नलिखित गुण हैं:

$$

$$F_0 = F_1 = 1, \ F_n = F_ {n-1} + F_ {n-2} $$$

यह तुरंत पुनरावृत्ति सूत्र का अर्थ है:

int Fibonacci(int n) { if(n == 1 || n == 2) return 1; return Fibonacci(n-1) + Fibonacci(n-2); } 

यदि पुनरावृत्ति "अंत से" एक संख्या की तलाश में है, तो निम्नलिखित विधि क्रमिक रूप से बीच स्थित सभी संख्याओं की गणना करती है $$$0$ और $$$एन$ :

 int dpFibonacci(int n) { int prev1 = 1; int prev2 = 1; int curr = 0; for(int j = 2; j < n; j++) { curr = prev1 + prev2; prev1 = prev2; prev2 = curr; } return curr; } 

यह स्पष्ट है कि पर्याप्त रूप से बड़े के लिए $$$एन$ यह एल्गोरिथ्म बहुत तेजी से काम करता है: यह कई बार मध्यवर्ती मूल्यों की गणना नहीं करता है। थोड़ा और जटिल उदाहरण पर विचार करें।

उदाहरण 1. आप एक टोल सीढ़ी पर चल रहे हैं। पर कदम रखना है $$$मैं$ आपको भुगतान करना होगा $$$a_i$ सिक्के। आप अगले चरण पर जा सकते हैं या एक पर कूद सकते हैं। कार्य: पास करने के लिए $$$एन$ कदम और संभव के रूप में कुछ सिक्के खर्च करते हैं।

यह स्पष्ट है कि प्रत्येक चरण पर कदम रखते हुए, हम "भुगतान" की संख्या को कम करते हैं, लेकिन हम एक बहुत ही महंगे चरण में भाग सकते हैं, जिससे हम बचना चाहेंगे। मूल्यों की एक सरणी बनाएँ $$$ड$ जिसमें $$$ज$ -यह स्थान उन सिक्कों की न्यूनतम (न्यूनतम) संख्या होगी जिन्हें प्राप्त करने के लिए खर्च किया जाना चाहिए $$$ज$ वें चरण। यह तुरंत स्पष्ट है कि $$$d_1 = a_1, \ d_2 = a_2$ । और फिर हम पिछले दो चरणों में कम से कम कदम उठाएंगे और कदम की लागत को स्वयं जोड़ेंगे:

$$

$$d_i = \ min \ left (d_ {i-1}, d_ {i-2} \ right) + a_ {i} $$$

हम समस्या की स्थितियों को थोड़ा बदलते हैं: मान लीजिए कि कुछ चरणों में आप सिक्के प्राप्त कर सकते हैं (इसका मतलब यह होगा कि $$$a_k <0$ )। एल्गोरिथ्म में क्या बदलने की आवश्यकता है ताकि यह सही परिणाम दे?


एक और उदाहरण पर विचार करें जो "द्वि-आयामी" गतिशीलता का उपयोग करता है।

उदाहरण 2. भूलभुलैया में है $$$एन \ _ मी$ कमरे, जिनमें से प्रत्येक में सोना होता है (एक पिंजरे में $$$(i, j)$ है $$$a_ {ij}$ सोना)। कार्य यह निर्धारित करना है कि एक बिंदु से अधिकतम मार्ग के साथ सोने की अधिकतम मात्रा क्या एकत्र की जा सकती है $$$(0,0)$ इस बिंदु पर $$$(n, m)$ अगर आप नीचे या दाईं ओर जा सकते हैं।

इसलिए, हम सेल का सबसे अच्छा मार्ग जानना चाहते हैं $$$(i, j)$ । हम यहां दो कोशिकाओं से प्राप्त कर सकते हैं - $$$(i-1, j)$ और $$$(i, j-1)$ । यह देखते हुए कि इन दो कोशिकाओं के लिए इष्टतम मार्ग ज्ञात हैं (वे किसी तालिका में संग्रहीत हैं $$$ड$ ), फिर सेल के लिए जवाब $$$(i, j)$ निम्नानुसार प्राप्त किया गया:

$$

$$d_ {ij} = \ max \ left (d_ {i-1j}, d_ {ij-1} \ right) + a_ {ij}। $$$

यह एक और क्लासिक गतिशील प्रोग्रामिंग कार्य है, जिसके संशोधन खेल प्रोग्रामिंग कार्यों में काफी आम हैं। इसी तरह के कार्य को यहां और अधिक विस्तार से समझाया गया है ।

अधिक चुनौतीपूर्ण कार्य

यदि वांछित है, तो एक गतिशील दृष्टिकोण को जहां चाहें वहां खराब किया जा सकता है। टिमस ऑनलाइन जज संग्रह के एक कार्य पर विचार करें।

समस्या का गणितीय सूत्रीकरण इस प्रकार है: किसी दिए गए अंक को पूर्ण वर्गों में विघटित करने के लिए आवश्यक न्यूनतम संख्या ज्ञात करना आवश्यक है।

पहले की तरह, मान लीजिए कि हम सभी संख्याओं के उत्तर जानते हैं $$$k-1$ कुछ सरणी में संग्रहीत हैं $$$ड$ और हम खोजना चाहेंगे $$$d_ {k}$ ।

यह नंबर लो $$$k$ और विश्लेषण करें कि क्या स्थितियां हो सकती हैं:

1. $$$k$ एक पूर्ण वर्ग है। इस मामले में $$$d_ {k} = 1$ ।
2. शायद पिछली संख्या $$$k-1$ एक पूर्ण वर्ग था। तो $$$d_ {k} = d_ {k-1} + 1$ ।

सामान्य तौर पर, पिछले एक इकाई को जोड़ने का विकल्प इतना बुरा नहीं लगता है।

हम इस प्रकार आगे बढ़ते हैं: हम एक अपघटन चाहते हैं $$$k = q ^ 2 + s$ ऐसा है

$$

$$d_ {q ^ 2} + d_s <d_ {k-1} + 1.$$

क्योंकि $$$q ^ 2$ - पूर्ण वर्ग तो $$$d_ {q ^ 2} = 1$ , और

$$

$$d_s <d_ {k-1},$$

यह है, हम एक विभाजन है कि बस से बेहतर है पाया $$$d_ {k-1} + 1$ , और इस मामले में जवाब होगा

$$

$$d_k = d_ {s} + d_ {q ^ 2} = d_s + 1.$$

निम्नलिखित समस्या पर विचार करें। लक्ष्य से एक सीढ़ी का निर्माण करना है $$$एन$ नियम के अनुसार क्यूब्स:

1. सीढ़ी के कम से कम दो चरण हैं;
2. एक सीढ़ी में दो समान चरण नहीं हो सकते;
3. सीढ़ियों के कदम आरोही क्रम में जाते हैं (यानी, अगला वाला पिछले वाले से बड़ा है)।

इस बार हम द्वि-आयामी गतिशीलता का निर्माण करेंगे। एक तालिका बनाएं $$$ड$ जिस स्थिति में $$$(i, j)$ सीढ़ियों की संख्या से मिलकर $$$मैं$ क्यूब्स जिनकी ऊंचाई अधिक नहीं है $$$ज$ । यदि यह काम करता है, तो हमारी समस्या का जवाब योग होगा

$$

$$\ _ \ _ सीमा_ {j = 1} ^ n d_ {nj}$$

तो, हम सीढ़ियों की संख्या खोजने की समस्या को हल करेंगे $$$मैं$ क्यूब्स जो लंबे होते हैं $$$ज$ । तस्वीर सीढ़ियों से पता चलता है कि गिर जाते हैं $$$d_ {74}$ :

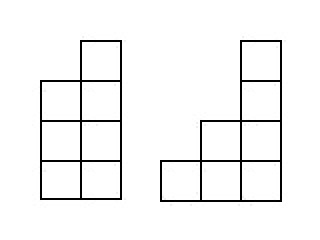
चूंकि हम सभी सीढ़ियों को जानते हैं, जिसमें कम क्यूब्स होते हैं, हम सीढ़ियों को "विभाजित" कर देंगे $$$(i, j)$ दाहिना स्तंभ। परिणाम एक सीढ़ी सी है $$$आई-जे$ क्यूब्स। के लिए उदाहरण $$$i = 9, \ j = 4$ :

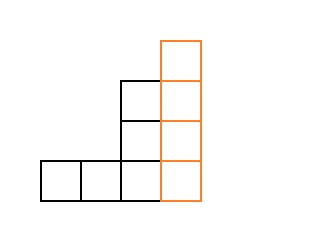
लेकिन ऐसी सीढ़ियों के लिए, परिणाम पहले से ही ज्ञात है, इसलिए हम ऐसी सभी सीढ़ियों के माध्यम से एक चक्र के साथ सॉर्ट करेंगे $$$k$ और सभी परिणाम जोड़ें। इस तरह से

$$

$$d_ {ij} = \ sum \ limit_ {k = 1} ^ {j-1} d_ {i-jj}।$$

अब हम सीढ़ियों की ऊँचाई को छाँटेंगे:

$$

$$d_ {ij} = \ sum \ limit_ {k = 1} ^ {j-1} d_ {i-jk}, \ j = \ overline {1, i}। $$$

अंत में, बदल रहा है $$$मैं$ से $$$1$ को $$$एन$ हमें जवाब मिल गया।

महत्वपूर्ण : हमारे मैट्रिक्स के निर्माण की प्रक्रिया में, इसे ध्यान में रखना आवश्यक है $$$d_ {ii} = 1$ , अन्यथा अन्यथा सीढ़ियों के कुछ प्रकार "खो" (जब "विभाजित") होंगे, लेकिन यह बिना कहे चला जाता है कि इस तरह की सीढ़ी समस्या की स्थितियों को संतुष्ट नहीं करती है, इसलिए उत्तर संख्या होगी $$$d_ {nn} - 1$ ।


अगला कार्य एक-आयामी सरणी का उपयोग करके हल किया गया है।

तो हमारे पास क्या है। पहला प्रवेश 2 शब्दों को जानता है। प्रत्येक व्यक्ति को सभी शब्द सिखाता है कि वह खुद को दो ः जानता है: युवा और बूढ़ा। बदले में, युवाओं को कई शब्दों के रूप में पढ़ाया जाता था जैसा कि वह पहले से ही जानता है, और पुराने को केवल एक शब्द सिखाया गया था। आपको यह जानने की जरूरत है कि कितने एनटीएस वास्तव में जानते हैं $$$K$ शब्द (इन ents modulo की संख्या को कम करना आवश्यक है $$$पी$ )।

समाधान काफी सरल है। एक सरणी बनाएँ $$$ड$ जिसमें $$$मैं$ -इस स्थान पर हम ents (मॉडुलो) की संख्या जमा करेंगे $$$पी$ ) जो जानते हैं $$$मैं$ शब्द। यह सब पहले प्रवेश से शुरू होता है, जो दो शब्दों को जानता है, इसलिए $$$d_2 = 1$ । और फिर सब कुछ सरल है:

• सभी ents जो विषम संख्या वाले शब्दों को जानते हैं, पुराने हैं और पिछले वाले से ही सीख सकते हैं। इसलिए विषम के लिए $$$i: \ d_i = d_ {i-1};$
• के रूप में ents के लिए जो शब्दों की एक समान संख्या को जानते हैं, ये सभी वे हैं जिन्हें कल्पित (युवा) से समान मात्रा में शब्द प्राप्त हुए हैं $$$+$ जिन्होंने पिछले (पुराने) से सीखा है; वह है, यहां तक ​​कि के लिए $$$मैं$ हमारे पास है $$$d_i = d _ {{i \ backslash 2}} + d_ {i-1}$ ।

यह गणना मोडुलो से निपटने के लिए बनी हुई है। विशाल संख्याओं को संग्रहीत नहीं करने के लिए, हम तुरंत सभी मूल्यों को याद रखेंगे।


उपयोग किए गए संसाधन:

1. टाइमस ऑनलाइन न्यायाधीश;
2. गतिशील प्रोग्रामिंग के बारे में थोड़ा ;
3. तुलना गुण मोडुलो।