Geekly articles weekly

अण्डाकार समीकरणों को हल करने के लिए संख्यात्मक तरीके

परिचय


सबसे आम अण्डाकार प्रकार का समीकरण पोइसन समीकरण है।
इस समीकरण के हल के लिए कई गणितीय भौतिकी की समस्याएं कम हो जाती हैं, उदाहरण के लिए, एक ठोस, प्रसार समस्याओं में स्थिर तापमान वितरण की समस्याएं, विद्युत आवेश की उपस्थिति में एक गैर-संचालन माध्यम में इलेक्ट्रोस्टैटिक क्षेत्र के वितरण की समस्याएं और कई अन्य।

कई मापों के मामले में अण्डाकार समीकरणों को हल करने के लिए, संख्यात्मक तरीकों का उपयोग अंतर समीकरणों या उनके सिस्टम को बीजगणितीय समीकरणों के सिस्टम में बदलने के लिए किया जाता है। समाधान की सटीकता कोऑर्डिनेट ग्रिड के चरण, पुनरावृत्तियों की संख्या और कंप्यूटर के बिट ग्रिड द्वारा निर्धारित की जाती है [1]

प्रकाशन का उद्देश्य उदाहरणों का उपयोग करके समाधान की विश्राम विधि के अभिसरण की जांच करने के लिए, डिरिचलेट और न्यूमैन सीमा स्थितियों के लिए पॉइसन समीकरण का समाधान प्राप्त करना है।

पोइसन समीकरण, अण्डाकार प्रकार के समीकरणों को संदर्भित करता है और एक-आयामी मामले में रूप [1] है:

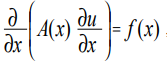
(1)

जहां x समन्वय है; यू (एक्स) वांछित कार्य है; ए (एक्स), एफ (एक्स) कुछ निरंतर समन्वय कार्य हैं।

हम मामले A = 1 के लिए एक आयामी पॉसों समीकरण को हल करते हैं, जो इस मामले में रूप लेता है:

(2)

अंतराल [xmin, xmax] पर हम एक समान समन्वय ग्रिड को एक चरण : के साथ परिभाषित करते हैं:

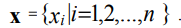
(3)

विचाराधीन समस्या के लिए पहली तरह की सीमा (डिरिचलेट की स्थिति) को निम्न रूप में दर्शाया जा सकता है:

(4)

जहां X1, xn क्षेत्र के सीमा बिंदुओं के निर्देशांक हैं [xmin, xmax]; जी 1, जी 2 - कुछ
निरंतर।

विचाराधीन समस्या के लिए दूसरी तरह की सीमा (नीमन की स्थिति) को निम्न रूप में दर्शाया जा सकता है:

(5)

एक समान समन्वय ग्रिड (3) पर डिरिचलेट सीमा की स्थिति को ध्यान में रखते हुए, हम अंतर प्राप्त करते हैं:

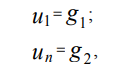
(6)

जहाँ u1, संयुक्त राष्ट्र के x (x) के क्रमशः x, xn के फलन के मान हैं।

ग्रिड (3) पर न्यूमैन सीमा की स्थिति को ध्यान में रखते हुए, हम प्राप्त करते हैं:

(7)

आंतरिक ग्रिड बिंदुओं के लिए समीकरण (2) को तोड़कर, हम प्राप्त करते हैं:

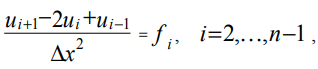
(8)

जहां ui, फाई समन्वय बिंदु x के साथ ग्रिड बिंदु पर यू (एक्स), एफ (एक्स) के मान हैं।

इस प्रकार, विवेकाधिकार के परिणामस्वरूप, हम आयाम के रैखिक बीजीय समीकरणों की एक प्रणाली प्राप्त करते हैं जिसमें क्षेत्र के आंतरिक बिंदुओं के लिए n (2) फॉर्म के n - 2 समीकरण और दो सीमा अंक [1] के लिए समीकरण (6) और (7) शामिल हैं।

निम्नलिखित ग्रिड (3) पर सीमा स्थितियों (4) - (5) के साथ समीकरण (2) के लिए एक संख्यात्मक समाधान के पायथन लिस्टिंग है।

लिस्टिंग समाधान
from numpy import* from numpy.linalg import solve import matplotlib.pyplot as plt x0=0#    xn=5#    n=100#    dx=(xn-x0)/(n-1)#      dx x=[i*dx+x0 for i in arange(0,n,1)]#      dx def f(i):#    return 2*sin(x[i]**2)+cos(x[i]**2) v1=1.0#     (1 - , 2 - ) g1=0.0#     v2=2.0#'     (1 - , 2 - ) g2=-0.5#     a=zeros([n,n])#     nxn b=zeros([1,n])#  -     1 xn #     , #       #  v1, v2 b[0,n-1]=g1; if v1==1: a[0,0]=1 elif v1==2: a[0,0]=-1/dx a[0,1]=1/dx; else: print(' v1   ') b[0,n-1]=g2; if v2==1: a[n-1,n-1]=1 elif v2==2: a[n-1,n-1]=1/dx a[n-1,n-2]=-1/dx; else: print(' v2   ') #     , #     for i in arange(1, n-1,1): a[i,i]=-2/dx**2 a[i,i+1]=1/dx**2 a[i,i-1]=1/dx**2 b[0,i]=f(i) u=linalg.solve(a,bT).T#  def viz(v1,v2): if v1==v2==1: return "          " elif v1==1 and v2==2: return "          " elif v2==1 and v2==1: return "          " plt.figure() plt.title("     ") y=[f(i) for i in arange(0,n,1)] plt.plot(x,y) plt.grid(True) plt.xlabel('x') plt.ylabel('f(x)') plt.figure() plt.title("    ") plt.xlabel('x') plt.ylabel('u(x)') plt.plot(x,u[0,:],label='%s'%viz(v1,v2)) plt.legend(loc='best') plt.grid(True) plt.show()


हमें मिलता है:









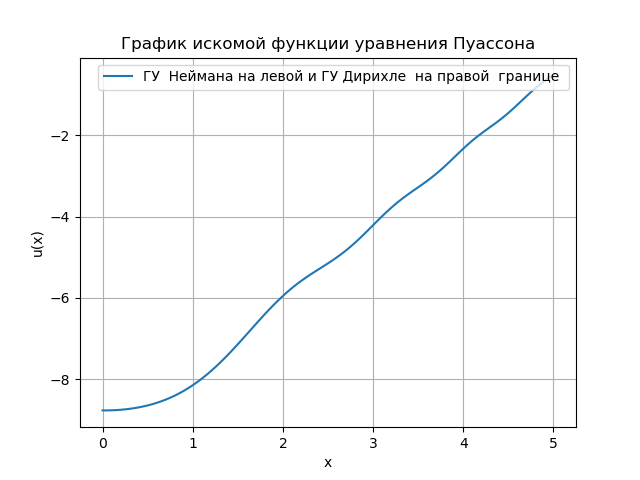
पायथन में मैंने जो कार्यक्रम विकसित किया है, वह सीमा की स्थितियों का विश्लेषण करने के लिए सुविधाजनक है। उपरोक्त पायथन सॉल्यूशन अल्गोरिद्म, नेप्सी फंक्शन की एक प्रणाली को हल करने के लिए Numpy फ़ंक्शन - u = linalg.solve (a, bT) .T का उपयोग करता है, जो वर्ग मैट्रिक्स {a} के साथ गति बढ़ाता है। हालांकि, माप की संख्या में वृद्धि के साथ, तीन विकर्ण मैट्रिसेस के उपयोग पर स्विच करना आवश्यक है, जिसके लिए समाधान बहुत सरल कार्य के लिए भी जटिल है, मुझे मंच पर एक उदाहरण मिला:

तीन विकर्ण मैट्रिक्स के साथ एक समाधान का उदाहरण
 from __future__ import print_function from __future__ import division import numpy as np import time ti = time.clock() m = 1000 A = np.zeros((m, m)) B = np.zeros((m, 1)) A[0, 0] = 1 A[0, 1] = 2 B[0, 0] = 1 for i in range(1, m-1): A[i, i-1] = 7 A[i, i] = 8 A[i, i+1] = 9 B[i, 0] = 2 A[m-1, m-2] = 3 A[m-1, m-1] = 4 B[m-1, 0] = 3 print('A \n', A) print('B \n', B) x = np.linalg.solve(A, B) # solve A*x = B for x print('x \n', x) print('NUMPY time', time.clock()-ti, 'seconds')


संवहन-प्रसार समीकरण के लिए ग्रिड डिरिचलेट समस्या के प्रत्येक दिशा में वर्दी पर संख्यात्मक समाधान का कार्यक्रम

[2]

(9)

हम संवहनी शब्द और पुनरावृत्ति छूट विधि के लिए केंद्रीय अंतरों द्वारा अनुमानों का उपयोग करते हैं। एफ (एक्स) = 1 और 6 (एक्स) = 0.10 के साथ समस्या के संख्यात्मक समाधान के लिए छूट पैरामीटर पर अभिसरण दर की निर्भरता के लिए। ग्रिड कार्य में:

(10)

हम तिरछे, निचले त्रिकोणीय और ऊपरी त्रिकोणीय मैट्रिक्स के योग के रूप में मैट्रिक्स ए का प्रतिनिधित्व करते हैं:

(10)

विश्राम विधि पुनरावृत्ति विधि के उपयोग से मेल खाती है :

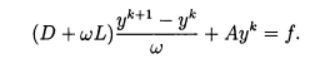
(11)

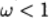
पर ऊपरी छूट के बारे में बात करते हैं, जब - कम विश्राम के बारे में।

कार्यक्रम सूचीकरण
 from numpy import * """       -  . .""" def relaxation(b, f, I1, I2, n1, n2, omega, tol = 1.e-8): h1 = I1 / n1 h2 = I2 / n2 d = 2. / h1**2 + 2. / h2**2 y = zeros([n1+1, n2+1]) ff = zeros([n1+1, n2+1]) bb = zeros([n1+1, n2+1]) for j in arange(1,n2,1): for i in arange(1,n1,1): ff [i,j] = f(i*h1, j*h2) bb[i,j] = b(i*h1, j*h2) #   - 10000 for k in arange(1, 10001,1): rn = 0. for j in arange(1,n2,1): for i in arange(1,n1,1): rr = - (y[i-1,j] - 2.*y [i, j] + y[i+1,j]) / h1**2 \ - (y[i,j-1] - 2.*y [i,j] + y[i,j+1]) / h2**2 \ + bb[i,j]*(y [i+1,j] - y [i-1,j]) / (2.*h1) - ff [i,j] rn = rn + rr**2 y[i,j] = y[i,j] - omega * rr / d rn = rn*h1*h2 if rn < tol**2: return y, k print ('   :') print (' 10000  =',sqrt(rn)) import matplotlib.pyplot as plt bcList = [0., 10.] sglist = ['-','--'] kk = 0 for bc in bcList: I1 = 1. I2 = 1. def f(x,y): return 1. def b(x,y): return bc n1 = 25 n2 = 25 m = 20 om = linspace(1., 1.95, m) it = zeros(([m])) for k in arange(0,m,1): omega = om[k] y, iter = relaxation(b, f, I1, I2, n1, n2, omega, tol=1.e-6) it[k] = iter s1= 'b =' + str(bc) sg = sglist[kk] kk = kk+1 plt.plot( om,it, sg, label = s1) plt.title("   \n     \n      $\\omega$") plt.xlabel('$\\omega$') plt.ylabel('iterations') plt.legend(loc=0) plt.grid(True) plt.show(
)

हमें मिलता है:



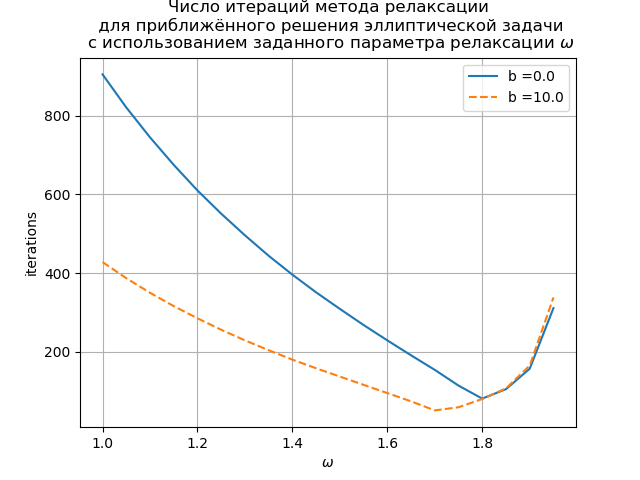
ग्राफ पोइसन समीकरण (b (x) = 0) और संवहन-प्रसार समीकरण (b (x) = 10) के लिए छूट पैरामीटर पर पुनरावृत्तियों की संख्या की निर्भरता को दर्शाता है। पॉइसन ग्रिड समीकरण के लिए, छूट पैरामीटर का इष्टतम मान विश्लेषणात्मक रूप से पाया जाता है, और पुनरावृत्ति विधि में परिवर्तित होता है ।

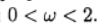
निष्कर्ष:

  1. सीमा स्थितियों की स्थापना के लिए एक लचीली प्रणाली के साथ पायथन में अण्डाकार समस्या का समाधान
  2. यह दिखाया गया है कि विश्राम विधि में एक इष्टतम सीमा है ( 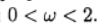) छूट पैरामीटर।

संदर्भ:

  1. रंडिन ई। ए। गणितीय भौतिकी की समस्याओं को हल करने के तरीके। - टैगानगर:
    टीआरटीयू, 2003 का प्रकाशन घर। - 120 पी।
  2. वाबिशचेविच पी.एन. न्यूमेरिकल मेथड्स: कम्प्यूटेशनल वर्कशॉप। - एम .: बुक हाउस
    लिब्रोकॉम, 2010. - 320 पी।

Source: https://habr.com/ru/post/hi418981/

More articles:


All Articles