स्कूल की पाठ्यपुस्तक I से कार्य

भाग I
भाग II
भाग III

"5 से 15 साल के बच्चों के लिए कार्य" पुस्तक से समस्या संख्या 38 के एल्गोरिथम समाधान पर विचार करें

राशि की गणना करें:

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ _ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ _ cdot100}$$

(उत्तर के 1% से अधिक की त्रुटि के साथ)

नीचे इस श्रृंखला की आंशिक रकम की गणना के लिए एक एल्गोरिथ्म दिया गया है (लिस्प) इन ड्रैकैट (ड्रैकैट आपको साधारण अंशों में गणना करने की अनुमति देता है):

#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000) 

पिछले दो उदाहरण एक त्रुटि के साथ गणना की गई ड्रैकैट



यह कार्यक्रम ऑनलाइन ide ideone.com और codepad.org पर चलाया जा सकता है।



यदि हम साधारण अंशों में आंशिक रकम पर विचार करते हैं, तो हम देख सकते हैं कि श्रृंखला का योग है

$$

$$\ frac {n} {n + 1}$$

मैं आपको याद दिला दूं $$$\ lim \ frac {n} {n + 1} = \ frac {1} {1+ \ _ frac {1} {n}} = \ frac {1} {1} = 1$ पर $$$n \ _ to $ infty$

डिफरेंशियल और इंटीग्रल कैलकुलस 363 (4) के पाठ्यक्रम का दूसरा खंड सामान्य मामले पर विचार करता है

$$

$$\ sum \ frac {1} {(\ Alpha + n) (\ Alpha + n +1)} = \ frac {1} {\ Alpha + 1}$$

पाठ्यक्रम "डेवलपर्स के लिए गणित" से कार्य :
एक क्रम में सदस्यों की संख्या ज्ञात कीजिए $$$\ frac {2n-1} {4n + 5}$ अंतराल के बाहर झूठ बोलना $$$(1- \ frac {1} {1000}; 1+ \ frac {1} {1000})$

चलिए लेख के मुख्य विषय पर चलते हैं।

आइए एक समस्या पुस्तक से एक और उदाहरण पर विचार करें।
४३ । खरगोशों की संख्या (फाइबोनैचि), एक क्रम बनाती है $$$(a_ {1} = 1), 1, 3, 5, 8, 13, 21, 34, ...,$ जिसमें $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ सभी के लिए $$$n = 1, 2, ...$ । संख्याओं का सबसे बड़ा सामान्य विभाजक ज्ञात कीजिए $$$a_ {100}$ और $$$a_ {99}$ ।

उत्तर: दो समीपवर्ती फाइबोनैचि संख्याएँ सहानुभूति हैं, अर्थात $$$\ gcd (u_ {n + 1}, u_ {n}) = 1$
(gcd सबसे बड़ा सामान्य भाजक है, अर्थात GCD)।

"पुस्तक से परे" गणित की पाठ्यपुस्तक से परे के पन्ने "[10-11]


अगले कार्य में, आपको सुनहरे अनुपात की गणना करने की आवश्यकता है , $$$\ frac {\ sqrt {5} + 1} {2} \ लगभग 1,618$ । [यह एक पोस्टकार्ड का पहलू अनुपात है जो एक वर्ग को काटते समय समान रहता है जिसका पक्ष पोस्टकार्ड का छोटा पक्ष होता है।]

५३ । फाइबोनैचि संख्याओं के अनुक्रम के लिए $$$a_ {n}$ कार्य 43 संबंध की सीमा पाते हैं $$$\ frac {a_ {n + 1}} {a_ {n}}$ प्रयास करते हुए $$$एन$ अनंत करने के लिए:

$$

$$\ frac {a_ {n + 1}} {a_ {n}} = 2, \ frac {3} {2}, \ frac {5} {3}, \ frac {8} {5}, \ frac { 13} {8}, \ frac {21} {13}, \ frac {34} {21}।$$

श्रृंखला के दो आसन्न सदस्यों के मतभेदों का प्रतिनिधित्व करने वाले खंडों पर विचार करें $$$\ frac {a_ {n + 1}} {a_ {n}}$ ।

यहां तक ​​कि श्रृंखला के सदस्य भी $$$\ frac {a_ {n + 1}} {a_ {n}}$ एक बढ़ते क्रम का प्रतिनिधित्व करते हैं $$$x_ {n}$

$$

$$\ frac {3} {2}, \ frac {8} {5}, \ frac {21} {13}, ...,$$

विषम पंक्ति के सदस्य $$$\ frac {a_ {n + 1}} {a_ {n}}$ घटते क्रम का प्रतिनिधित्व करें $$$y_ {n}$

$$

$$2, \ frac {5} {3}, \ frac {13} {8}, ...,$$

एम्बेडेड अंतराल लेम्मा द्वारा (अंतर और अभिन्न कलन का पाठ्यक्रम, 38)

$$

$$c = \ lim x_ {n} = \ lim y_ {n}$$

एक बिंदु पर हमारी पंक्ति के लिए $$$सी$ निष्पक्ष समानता $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = \ frac {a_ {n + 1}} {a_ {n}}$

भाग देनेवाला $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ पर $$$a_ {n + 1}$ हमें समीकरण मिलता है $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = 1 + \ frac {a_ {n}} {a_ {n + 1}}$ ।
बदलकर $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = x, \ frac {a_ {n}} {a_ {n + 1}} = \ frac {1} {x}$ हमें द्विघात समीकरण मिलता है $$$x = 1 + \ frac {1} {x}$ ।

यदि जियोजेब्रा प्रोग्राम में हम अंक 2 और जोड़ते हैं $$$\ frac {3} {2}$ । $$$\ frac {3} {2}$ और $$$\ frac {5} {3}$ । $$$\ frac {5} {3}$ और $$$\ frac {8} {5}$ आदि - एक आत्म-समान आंकड़ा प्राप्त करें




सामान्य तौर पर, पायथन में फाइबोनैचि संख्याओं की गणना के लिए एक मानक एल्गोरिथ्म है।
यह एल्गोरिथ्म Python.org पर उपलब्ध है

 def fib(n): a, b = 0, 1 while a < n: print(a) a, b = b, a+b fib(100) 

आप लिंक की जाँच कर सकते हैं
इस एल्गोरिथ्म को बदलें ताकि यह सुनहरा अनुपात को एक अनुमान लगाता है। दो आसन्न संख्याओं के लिए a और b, हम योग a + b को b से विभाजित करेंगे

 def fib(n): a, b = 0.0 , 1.0 while a < n: print((a+b)/b) a, b = b, a+b fib(100) 

आप लिंक की जाँच कर सकते हैं

सुनहरे अनुपात के संबंध में SICP ट्यूटोरियल के कुछ कार्य इस प्रकार हैं ।


टास्क बुक "5 से 15 साल के बच्चों के लिए कार्य" से निम्नलिखित उदाहरण
५४ । अनंत निरंतर अंश की गणना करें

$$

$$1 + \ frac {1} {2 + \ frac {1} {1+ \ _ frac {1} {2+ \ _ frac {1} {1 + \ frac {1} {2 + ...}}}}}$$

युपीडी। समीकरण पर विचार करें

$$

$$\ अल्फा = 1+ \ frac {1} {2 + \ frac {1} {\ अल्फा}}$$

236 और 235 के अनुसार पुस्तक "संख्या सिद्धांत" से:

$$

$$\ Alpha = \ frac {P_ {1} \ Alpha + P_ {0}} {Q_ {1} \ Alpha + Q_ {0}}$$

हम मूल्यों की एक तालिका की रचना करते हैं $$$P_ {n}$ और $$$Q_ {n}$ पर $$$n = 0,1:$



ताकि $$$\ अल्फा = \ frac {3 \ अल्फा + 1} {2 \ अल्फा + 1}, 2 \ अल्फा ^ {2} - 2 \ अल्फा -1 = 0$

और कब से $$$\ अल्फा> 0,$

$$

$$\ अल्फा = \ frac {1 + \ sqrt {3}} {2}$$

पुस्तक की समस्या पर विचार करें "गणित की पाठ्यपुस्तक के पृष्ठों के पीछे" [10-11]
४ । वह नंबर दिखाएं $$$\ sqrt {1+ \ sqrt {1 + \ sqrt {1 + ...}}}$ संख्या के बराबर $$$\ varphi$ स्वर्णिम अनुपात को परिभाषित करना।

विकल्प पर विचार करें $$$x_ {n} = \ sqrt {c + \ sqrt {c + ... + \ sqrt {c}}}$
अंतर और अभिन्न कलन का पाठ्यक्रम, 35 (2)

इस तरह से $$$x_ {n + 1}$ से प्राप्त किया $$$x_ {n}$ सूत्र के अनुसार

$$

$$x_ {n + 1} = \ sqrt {c + x_ {n}}$$

... मुख्य प्रमेय द्वारा, विकल्प $$$x_ {n}$ कुछ सीमित सीमा है $$$एक$ । इसे निर्धारित करने के लिए, हम समानता में सीमा को पास करते हैं

$$

$$x_ {n + 1} ^ {2} = c + x_ {n};$$

हम इस तरह से प्राप्त करते हैं कि $$$एक$ द्विघात समीकरण को संतुष्ट करता है

$$

$$a ^ {2} = c + a$$

इस समीकरण में विभिन्न संकेतों की जड़ें हैं; लेकिन वह सीमा जो हमें रुचती है $$$एक$ नकारात्मक नहीं हो सकता है, इसलिए, यह सकारात्मक जड़ के बराबर है:

$$

$$a = \ frac {\ sqrt {4c + 1} + 1} {2}$$

जिससे हम यह निष्कर्ष निकाल सकते हैं कि "स्वर्ण अनुपात" समीकरण का एक समाधान है $$$a ^ {2} = c + a$
पर $$$c = 1$ ।


आगे, डिफरेंशियल और इंटीग्रल कैलकुलस, 35 (3) के पाठ्यक्रम में, व्युत्क्रम संख्या की गणना के लिए एक एल्गोरिथ्म पर विचार किया जाता है।

चलो $$$सी$ कोई पॉजिटिव नंबर है, और डाल दीजिए $$$x_ {n} = cy_ {n}$ । ऊपर लिखे गए पुनरावृत्ति संबंध को निम्न द्वारा प्रतिस्थापित किया जाएगा:

$$

$$y_ {n + 1} = y_ {n} (2 - cy_ {n})$$

प्रारंभिक मूल्य ले रहा है $$$y_ {0}$ शर्त के तहत: $$$0 <y_ {0} <\ frac {1} {c}$ हमें वह मिलता है $$$y_ {n}$ नीरसता बढ़ रही है, करने के लिए करेंगे $$$\ frac {1} {c}$ । इस योजना के अनुसार, गिनती मशीनों पर, व्युत्क्रम संख्या की गणना की जाती है $$$सी$ ।

उलटा संख्या गणना एल्गोरिथ्म $$$सी$ पायथन में:
( Ideone.com और codepad.org )

 def reciprocal(c,y0,n): arr=[] for i in range(n): arr.append(y0) y0=y0*(2-c*y0) return arr 

पारस्परिक कार्य इनपुट के रूप में एक संख्या लेता है $$$सी$ प्रारंभिक मूल्य $$$y_ {0}$ पुनरावृत्तियों की संख्या $$$एन$ और संख्या के लिए "सन्निकटन" की एक सरणी देता है $$$\ frac {1} {c}$ ।
$$$y_ {0} = 0.1$ पर $$$c <10$
$$$y_ {0} = 0.01$ पर $$$10 <c <100$
$$$y_ {0} = 0.001$ पर $$$100 <c <1000$
आदि
पारस्परिक कार्य विभिन्न के साथ कैसे कार्य करता है, इसके उदाहरण $$$सी$

 >>> reciprocal(3,0.1,10) 

[0.1, 0.17, 0.2533, 0.31411733000000003, 0.3322255689810133, 0.3333296519077525
0.3333333332926746, 0.3333333333333333337, 0.333333333333333333, 0.333333333333337]

 >>> reciprocal(8,0.1,10) 

[0.1, 0.12, 0.1248, 0.12499968, 0.1249999999991808, 0.125, 0.125, 0.125, 0.125, 0.125]

 >>> reciprocal(5,0.1,10) 

[0.1, 0.15000000000000002, 0.18750000000000003, 0.19921875000000003, 0.19999694824218753, 0.1999999999534339, 0.20000000000000004, 0.19999999999999998,
0.19999999999999998, 0.19999999999999998]

ज्यामितीय व्याख्या

चलो उलटे संख्या को अनुमानित करने के लिए स्पर्शरेखा विधि का उपयोग करने का प्रयास करें।
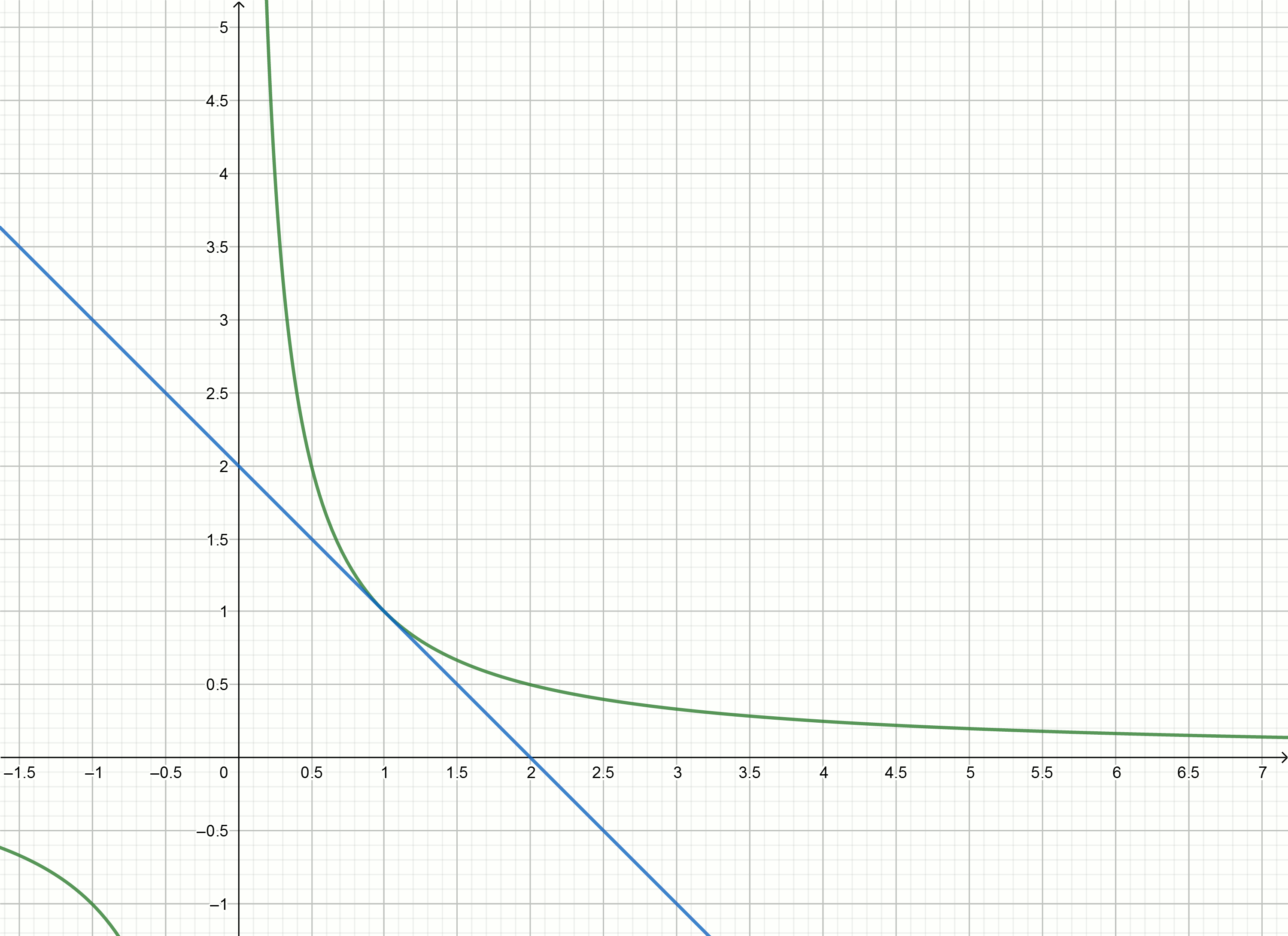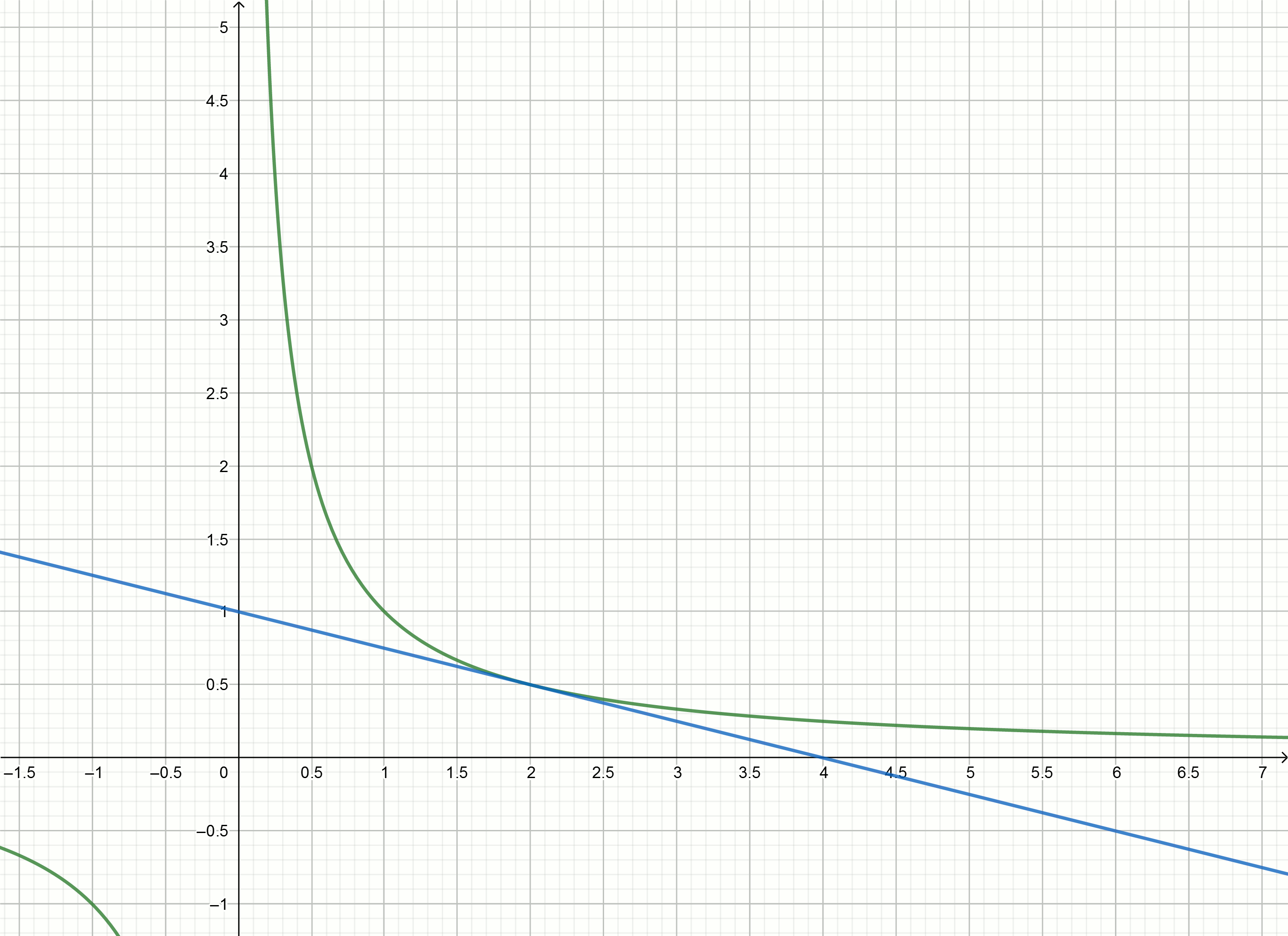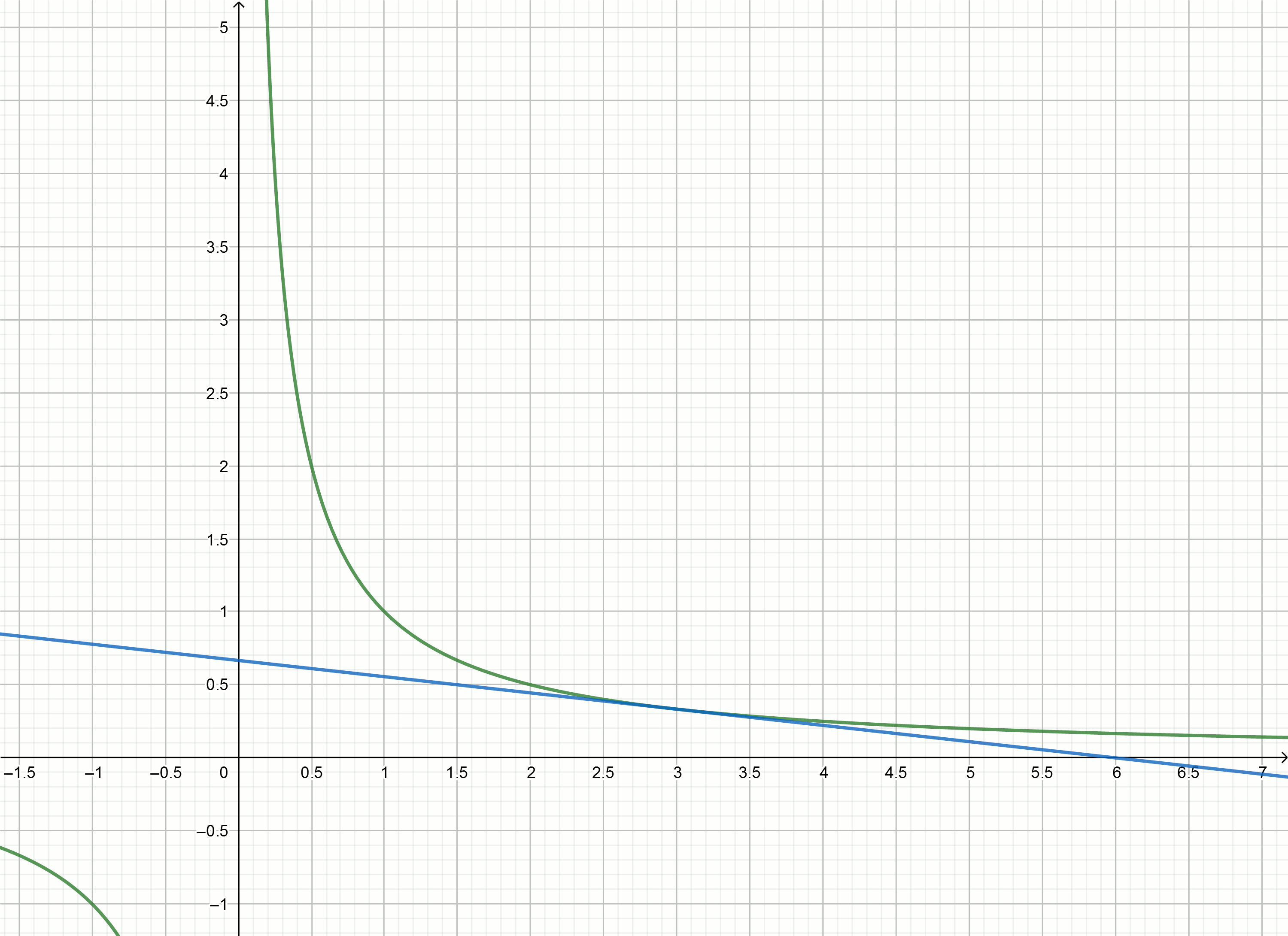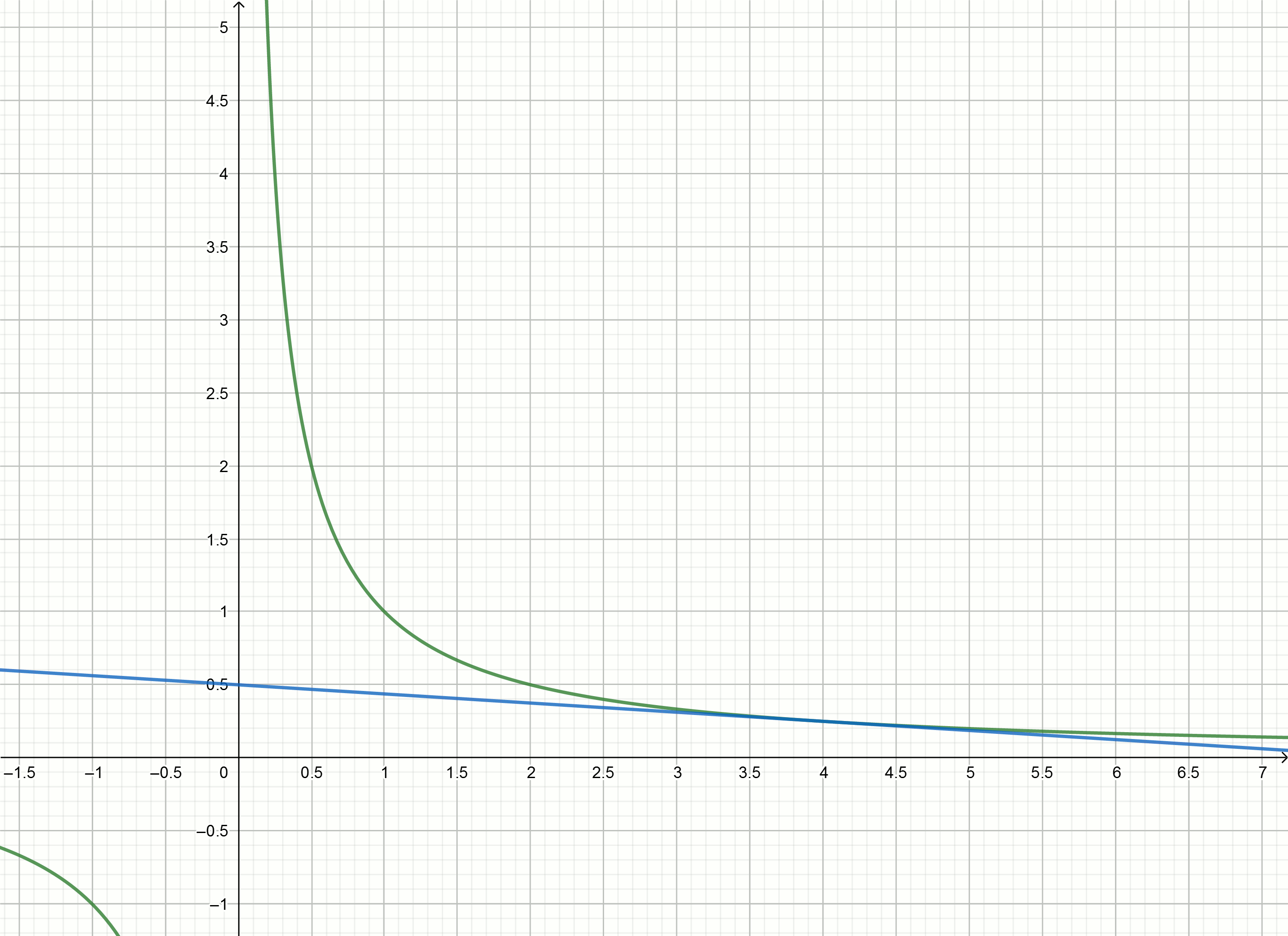
स्पर्शरेखा $$$y = f '(x_ {0}) (x-x_ {0}) + f (x_ {0})$ ग्राफ का कार्य करने के लिए $$$y = \ frac {1} {x}$ सूत्र द्वारा व्यक्त किए गए हैं $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}}$

स्थानापन्न संख्याएँ $$$1,2,3,4, ...$ के बजाय $$$x_ {0}$ हम स्पर्शरेखा के समीकरणों को प्राप्त करते हैं

$$

$$y = 2-x$$

$$

$$y = 1- \ frac {x} {4}$$

$$

$$y = \ frac {2} {3} - \ frac {x} {9}$$

$$

$$y = \ frac {1} {2} - \ frac {x} {16}$$

ये रेखांकन बनाएँ


यदि आप हाइपरबोला को नीचे ले जाते हैं $$$\ अल्फा$ , तो यह बिंदु पर अनुपस्थिति अक्ष को पार करता है $$$\ frac {1} {\ Alpha}$ ।
स्पर्शरेखा समीकरण को परिवर्तित किया जाता है $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - \ अल्फा$
इसके अलावा, स्पर्शरेखा के समीकरण को शून्य और व्यक्त करने के लिए बराबर करना $$$x$ हमें समीकरण मिलता है $$$x = x_ {0} - \ frac {f (x_ {0})} {f '(x_ {0}) $$

के बदले $$$च (x_ {0})$ स्थानापन्न $$$\ frac {1} {x_ {0}} - \ Alpha$
के बदले $$$f '(x_ {0})$ स्थानापन्न $$$- \ frac {1} {x_ {0} ^ {2}}$

हमें अभिव्यक्ति मिलती है $$$x = x_ {0} + (\ frac {1} {x_ {0}} - \ Alpha) x_ {0} ^ {2}$
कोष्ठक का विस्तार, हमें मिलता है $$$x = x_ {0} + x_ {0} - \ Alpha x_ {0} ^ {2}$

हम स्थानापन्न $$$0.1$ समीकरण में $$$x = x_ {0} (2- \ अल्फा x_ {0})$ और देखें कि "मूल्य किस माध्यम से चलेंगे" $$$x$ पर $$$\ अल्फा = 2$ हमें मिलता है $$$0.1, 0.18, 0.29, 0.42, 0.49, 0.5$

समीकरण में इन मूल्यों को प्रतिस्थापित करना $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - 2$ हमें प्रत्यक्ष मिलता है

$$

$$y = 0.111 - \ frac {x} {0.897}$$

$$

$$y = 0.222 - \ frac {x} {0.81}$$

$$

$$y = 0.816 - \ frac {x} {0.504}$$

$$

$$y = 0.857 - \ frac {x} {0.49}$$

$$

$$y = 1.5 - \ frac {x} {0.326}$$

$$

$$y = 2 - \ frac {x} {0.25}$$

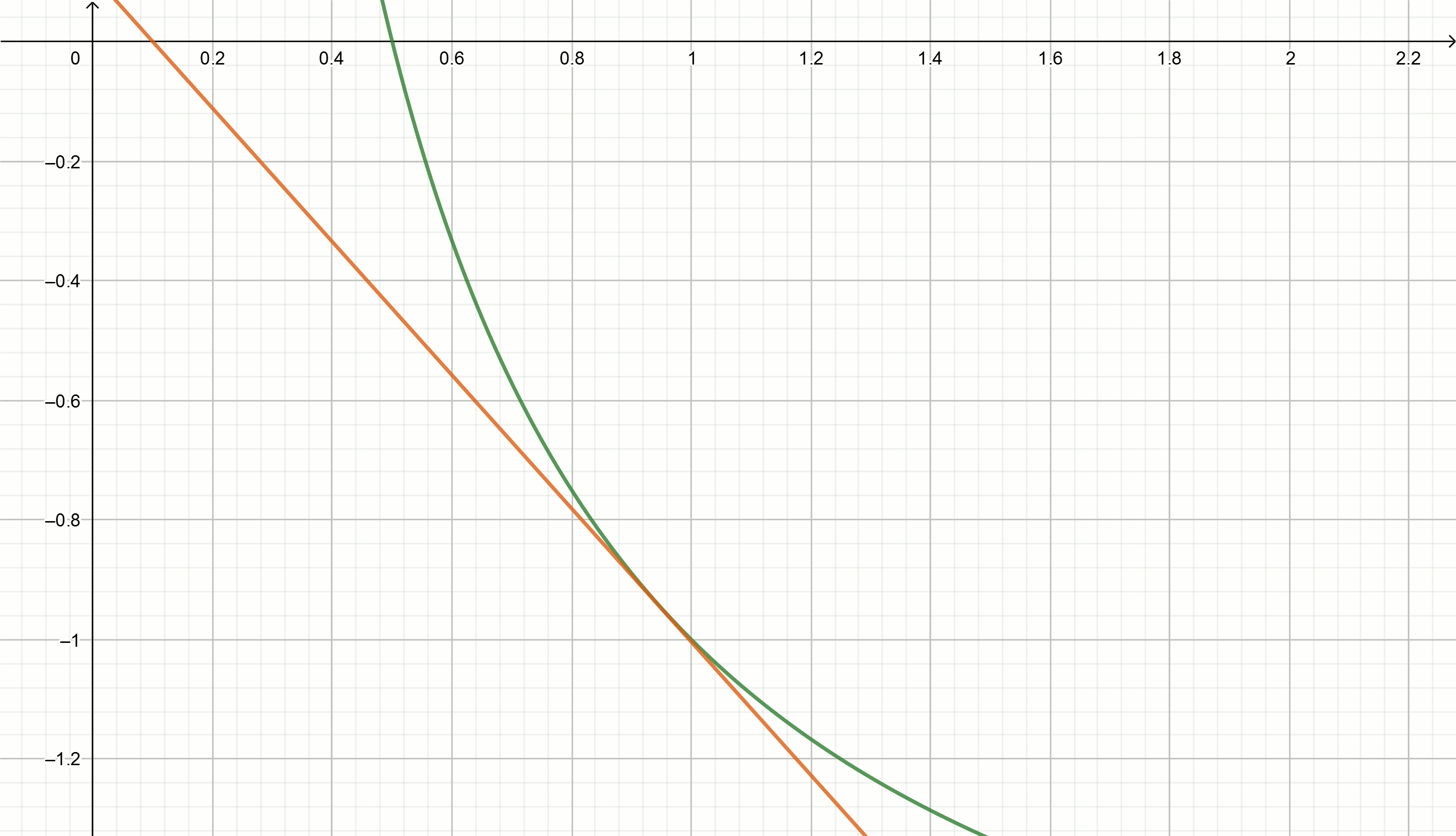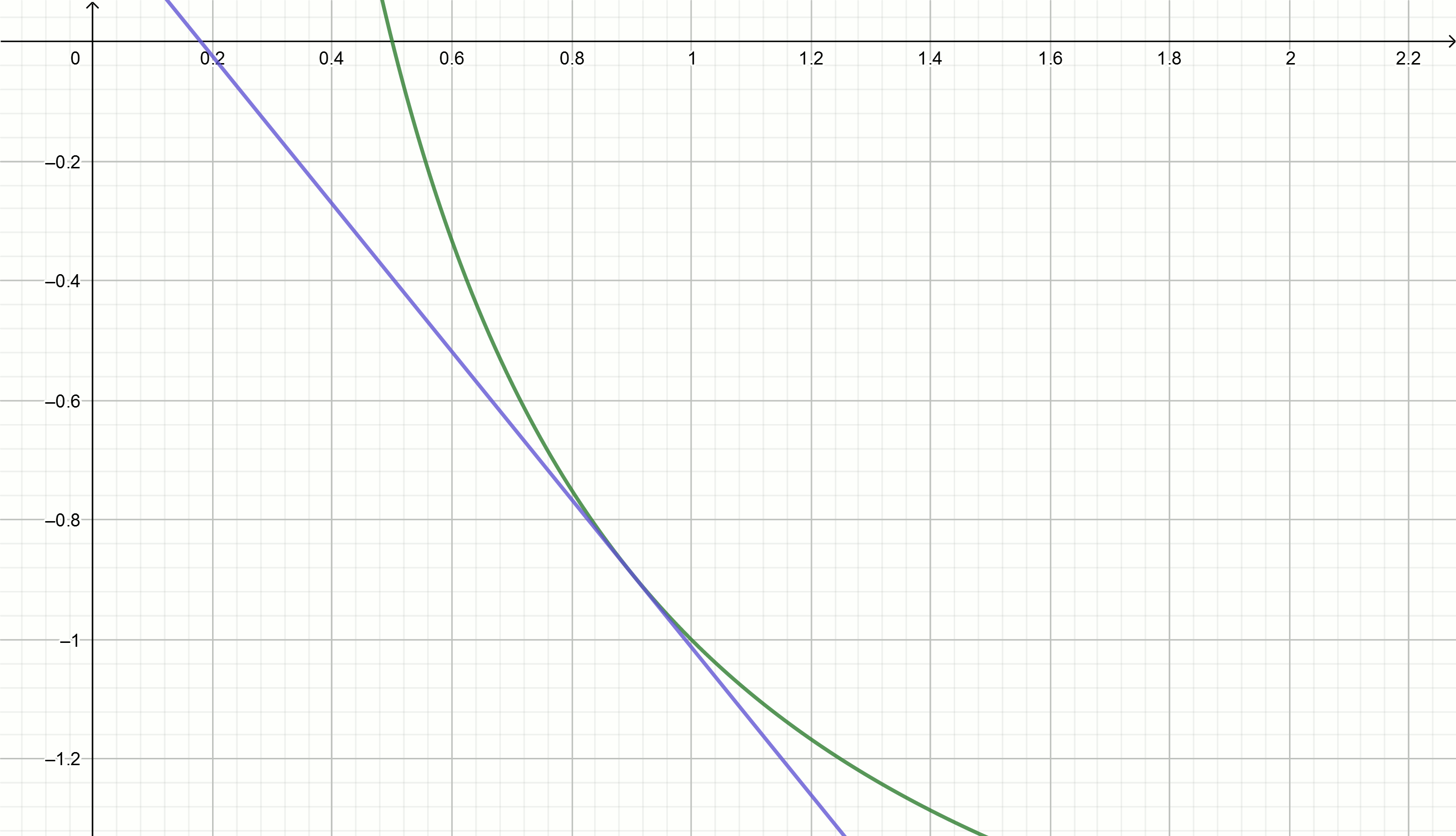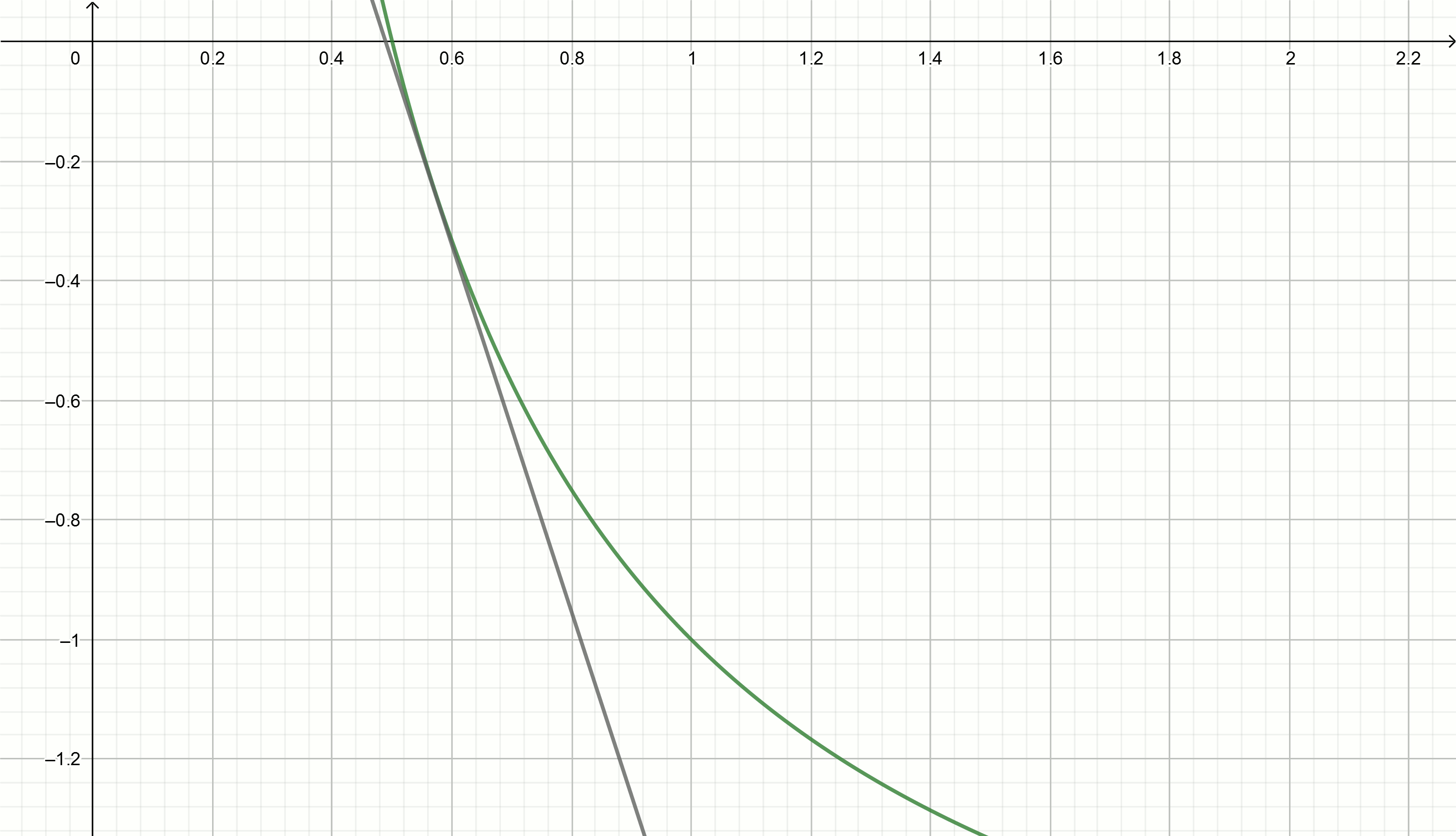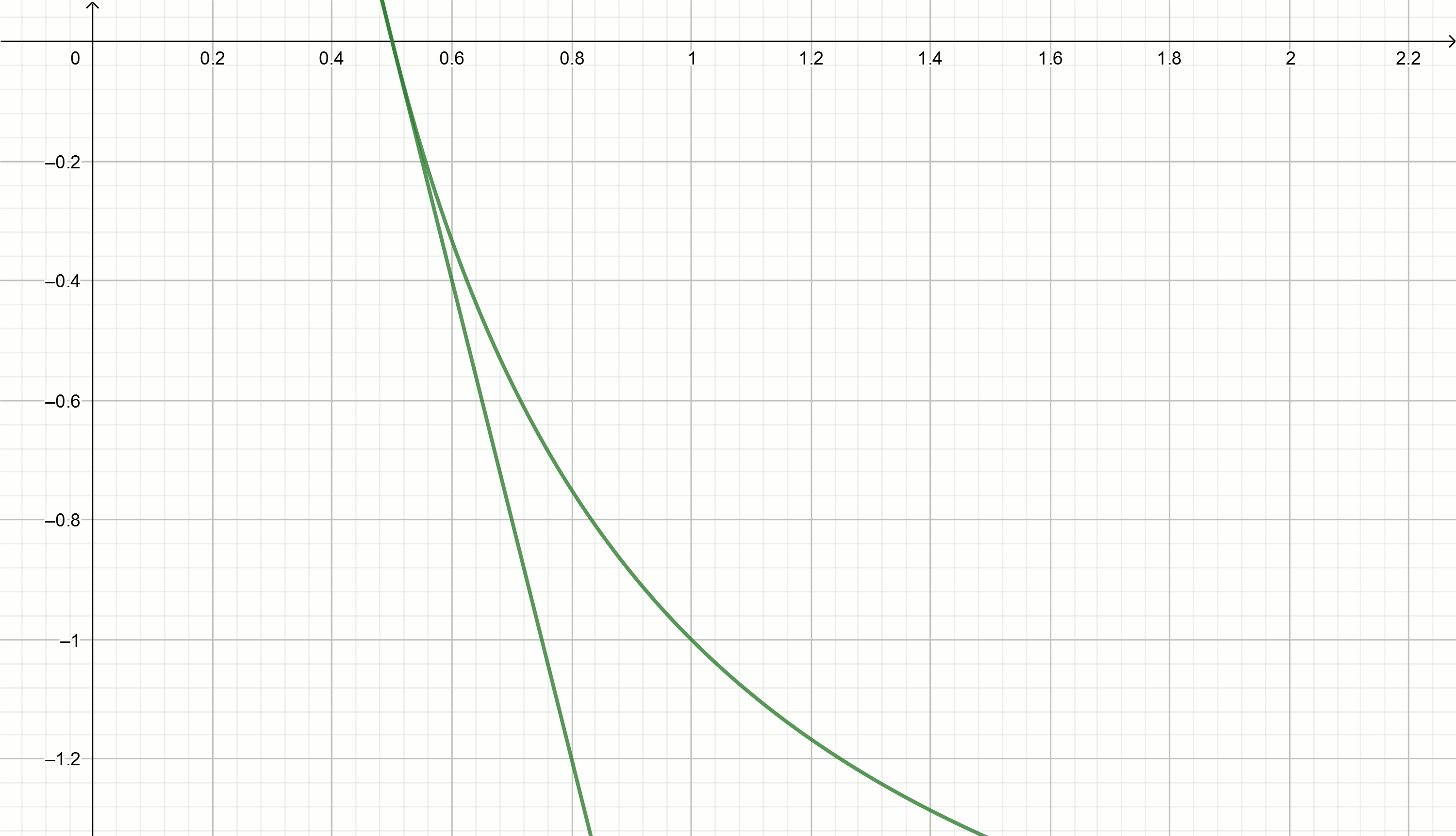
वर्गमूल निष्कर्षण

तर्कहीन अभिव्यक्तियों पर लौटते हुए, हम वर्गमूल निकालने की एक पुनरावृत्ति विधि पर विचार करते हैं।
हम हेरोन पुनरावृत्ति विधि का उपयोग करके एक एल्गोरिथ्म लिखेंगे

$$

$$x_ {n + 1} = \ frac {1} {2} (x_ {n} + \ frac {a} {x_ {n}})$$

 def square_root(a,n): # a -  , n -   x0=1 #    1 arr=[] for i in range(n): arr.append(x0) #      x0=0.5*(x0+a/x0) #      return arr print square_root(2,10) 

codepad.org

राफेल बॉम्बेली द्वारा उपयोग किए गए निरंतर अंशों का उपयोग करके वर्गमूल की गणना

मान ज्ञात करने के लिए $$$\ sqrt {n}$ , पहले हम इसके पूरे सन्निकटन को परिभाषित करते हैं: $$$\ sqrt {n} = a \ pm r$ जहाँ $$$0 <r <1$ । तो $$$n = (a + pm r) ^ {2} = a ^ {2} \ pm 2ar + r ^ {2}$ । यहाँ से उस कटौती को करना आसान है $$$r = {\ frac {| n-a ^ {2} |} {2a \ pm r}}$ । सूत्र में परिणामी अभिव्यक्ति की जगह $$$\ sqrt {n} = a \ pm r$ , हम एक निरंतर भिन्न विस्तार प्राप्त करते हैं:

$$

$$a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac = na ^ {2}}} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}$$

तो, हम एक निरंतर अंश में अपघटन का उपयोग करके वर्गमूल निष्कर्षण एल्गोरिदम लिख सकते हैं

 def square_root(n,a,n_count): # n- , a -    x0=a #    a arr=[] for i in range(n_count): #       a arr.append(x0-a) #  a x0=2*a+(na*a)/x0 return arr print square_root(2.0,1.0,10) 

codepad.org

सामान्य तौर पर, वास्तविक और जटिल संख्या, साथ ही एक या एक से अधिक चर के कार्य, निजी अंक और भाजक हो सकते हैं।
पूर्णांक भाग को निकालने की विधि एक को एक अपरिमेय संख्या के रूप में एक अपरिमेय अंश के रूप में दर्शाती है, जो कि अंशधारियों में इकाइयों के साथ होता है (जो लगातार अंश बराबर होता है)।
यहाँ एक संख्या के निरंतर भिन्न विस्तार का एक उदाहरण है $$$\ sqrt {5}$ "बीजगणित" पुस्तक से

$$

$$\ sqrt {5} -2 = \ frac {(\ sqrt {5} -2) (\ sqrt {5} +2)} {\ sqrt {5} +2} = \ frac {1} {\ sqrt { 5} +2}$$

इस तरह से $$$\ sqrt {5} = 2+ \ frac {1} {\ sqrt {5} +2}$

संख्या के पूर्णांक भाग का चयन करें $$$\ sqrt {5} +2: E (\ sqrt {5} +2) = 4$ । इसलिए, $$$\ sqrt {5} +2$ के रूप में प्रतिनिधित्व किया जा सकता है $$$4 + \ अल्फा$ । यह स्पष्ट है कि $$$\ Alpha = \ sqrt {5} + 2-4 = \ sqrt {5} -2$ इसलिये $$$\ sqrt {5} + 2 = 4 + \ sqrt {5} + 2$ । फिर, हम दूसरे शब्द के अंश में तर्कहीनता को नष्ट करते हैं:

$$

$$\ sqrt {5} -2 = \ frac {1} {\ sqrt {5} +2}$$

परिणाम है:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}$$

चलिए एक और समान कदम उठाते हैं:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}}$$

यह देखना आसान है कि पूरे भाग को अलग करने और इस उदाहरण में एक निरंतर अंश के गठन की प्रक्रिया का कोई अंत नहीं है। प्रत्येक नए हर में दिखाई देगा $$$4$ और कार्यकाल $$$\ sqrt {5} -2$ । इसलिए, यह स्पष्ट है कि $$$\ sqrt {5}$ एक अनंत निरंतर अंश के रूप में दर्शाया गया है:

$$

$$\ sqrt {5} = [2, 4, 4, 4, ...]$$

परिकल्पना

अगर $$$d \ in \ mathbb {N}, \ sqrt {d} \ notin \ mathbb {N}$ फिर संख्या का निरंतर अंश $$$\ sqrt {d} + [\ sqrt {d}]$ पूरी तरह से आवधिक।
Evarist Galois ने इस परिकल्पना को साबित किया।

यानी यदि अंश के गैर-आवधिक भाग के लिए $$$[1; 2,2,2, ...] = \ sqrt {2}$ पूरा हिस्सा जोड़ें $$$[\ sqrt {2}] = 1$ तब हमें एक शुद्ध आवधिक अंश प्राप्त होता है $$$[2,2,2, ...]$ ।

$$$\ sqrt {3} = [1; 1,2, ...];$
$$$\ sqrt {3} +1 = [2,1, ...]$

$$$\ sqrt {5} = [2; 4,4,4, ...];$
$$$\ sqrt {5} +2 = [4,4,4, ...]$

$$$\ sqrt {6} = [2; 2,4, ...];$
$$$\ sqrt {6} +2 = [4,2, ...]$

$$$\ sqrt {13} = [3; 1,1,1,1,6, ...];$
$$$\ sqrt {13} +3 = [6,1,1,1,1,1, ...]$


अगर बॉम्बेली विधि के अनुसार रूट अपघटन में

$$

$$\ sqrt {n} = a a pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ _ frac {| na ^ { 2} |} {2a \ pm \ cdots}}}}}}}$$

पहले कार्यकाल में जोड़ें $$$एक$ , हम एक शुद्ध आवधिक अंश प्राप्त करते हैं

$$

$$\ sqrt {n} + a = 2a \ pm {\ frac {| na ^ {2} |}} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ _ frac {| ^ {2} |} {2a \ pm \ cdots}}}}}}}$$

यह अंश को अधिक परिचित रूप में लाने के लिए बना रहता है (अंश में इकाइयों के साथ)।
अंश के अंश और हर को विभाजित करें $$$| n-a ^ {2} |$ हमें अभिव्यक्ति मिलती है

$$

$$\ sqrt {n} + a = 2 a a pm {\ frac {1} {\ frac {2a} {| na ^ {2} |} \ pm {\ frac {1} {2a \ pm {\ frac {| 1} {\ frac {2a} {| na ^ {2} |} \ pm \ cdots}}}}}}} $$$

इस तरह से

$$

$$\ sqrt {2} +1 = 2+ \ frac {1} {\ frac {2} {1} + \ frac {1} {2 + \ frac {1} {\ frac {2} {1} +। ..}}} = [2,2,2, ...]$$

$$

$$\ sqrt {3} +1 = 2+ \ frac {1} {\ frac {2} {2} + \ frac {1} {2 + \ frac {1} {\ frac {2} {2} +। ..}}} = [2,1, ...]$$

$$

$$\ sqrt {5} +2 = 4+ \ frac {1} {\ frac {4} {1} + \ frac {1} {4 + \ frac {1} {\ frac {4} {1} +। ..}}} = [4,4,4, ...]$$

$$

$$\ sqrt {6} +2 = 4+ \ frac {1} {\ frac {4} {2} + \ frac {1} {4 + \ frac {1} {\ frac {4} {2} +। ..}}} = [4,2, ...]$$

$$

$$\ sqrt {13} +3 = 6+ \ frac {1} {\ frac {6} {4} + \ frac {1} {6 + \ frac {1} {\ frac {6} {4} +। ..}}} = [6, \ frac {3} {2}, ...]$$

हम एक प्रोग्राम लिखेंगे जो निरंतर अंश सन्निकटन की गणना करता है $$$[6, \ frac {3} {2}, ...]$

 #lang racket (define continued_fraction ( lambda (n) (if (= n 0) 1 (+ 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) ))) (continued_fraction 4) 

codepad.org
चौथे चरण में हम प्राप्त करते हैं $$$6 \ frac {3818} {6305}$ जो बराबर है $$$6.60555114 ...$ के रूप में जबकि $$$\ sqrt {13} +3 \ लगभग 6.60555127$ ।




PS समस्या का समाधान करें ("5 से 15 वर्ष के बच्चों के लिए समस्याएँ")
२ ।। सिद्ध करें कि किसी संख्या का विभाजन शेष है $$$2 ^ {p-1}$ विषम प्रधान
$$$पी$ के बराबर है $$$1$
(उदाहरण: $$$2 ^ {2} = 3 ए + 1, 2 ^ {4} = 5 बी + 1, 2 ^ {6} = 7c + 1, 2 ^ {10} -1 = 1023 = 10 \ cdot 93)$ ।
इस समस्या को क्वांटम पत्रिका के अमेजिंग एडवेंचर्स ऑफ कंटिन्यूअस फ्रैक्शन्स ऑफ आर्टिकल में माना जाता है।

पुस्तकें:
"5 से 15 वर्ष के बच्चों के लिए कार्य" वी। आई। अर्नोल्ड।
"विभेदक और अभिन्न कलन का कोर्स" जी। एम। फिकेनथोल्ट्ज़
"नंबर थ्योरी" A. A. Buchstab
"गणित की पाठ्यपुस्तक के पन्नों के पीछे" एन। वाई। विलेनकिन, एल। पी। शिबासोव, जेड एफ। शिबासोवा
"बीजगणित" एन। हां। विलेनकिन, आर.एस. गुटेर, एस। आई। श्वार्जबर्ड
डिजिटल अंकगणित Ercegovac Milos D., Lang Tomas
"कंप्यूटर कार्यक्रमों की संरचना और व्याख्या" हेरोल्ड एबेल्सन, जेराल्ड ससमन

यह भी देखें
लेख "एक कार्य पर जो अब साक्षात्कार में पेश नहीं किया जाता है।"
विभिन्न कंपनियों के लिए स्पाइस आईटी रिक्रूटमेंट के ब्लॉग पोस्टिंग साक्षात्कार कार्य।
यांडेक्स में साक्षात्कार के लिए कार्य ।
इस वीडियो में, ए। सवतेव ने टेस्ला में साक्षात्कार के साथ समस्याओं को हल किया।