🧓 🎅🏾 👇🏽 शेयर बाजारों में तकनीकी संकेतक कैसे हैं 🧝🏽 ☹️ 🥈

जो भी कभी स्टॉक या क्रिप्टोक्यूरेंसी बाजारों में रुचि रखते हैं, उन्होंने इन अतिरिक्त लाइनों को देखा है। और आपने शायद अनुभवी व्यापारियों से राय सुनी है कि वे काम नहीं करते हैं और वे कुछ भी उपयोग नहीं करते हैं। लेकिन वे बहुत मदद करते हैं और मेरे ट्रेडिंग टर्मिनल, जिसे मैं आलसी रूप से दिन में एक बार देखता हूं, नीचे दी गई तस्वीर जैसा कुछ दिखता है।

कैसे वे सभी एक ही व्यवस्था कर रहे हैं? और यह किसके लिए उपयोगी हो सकता है? आप निश्चित रूप से इस से परिचित हो जाना चाहिए अगर:

आप उन्हें अपने व्यापार में उपयोग करें
क्या आप एक ट्रेडिंग रोबोट लिखने की योजना बना रहे हैं
क्या आप खुद एक ट्रेडिंग रणनीति लागू करना चाहते हैं

एक तकनीकी संकेतक सबसे अक्सर एक खिड़की, वजन या पुनरावृत्ति की कीमतों और संस्करणों का कार्य है जो मोमबत्तियों के एक सरणी TOHLCV (यूनिक्स समय, खुला, उच्च, निम्न, बंद, वॉल्यूम) के एक सरणी के रूप में विनिमय से आता है। विभिन्न फ़िल्टरिंग, अधिकतम-न्यूनतम या अन्य संकेतक भी बाद की गणना के आधार के रूप में उपयोग किए जा सकते हैं।

मूविंग एवरेज (SMA)

संकेतकों को लागू करते समय, कार्यात्मक प्रोग्रामिंग दृष्टिकोण का उपयोग करना बहुत सुविधाजनक है। उदाहरण के लिए, एक चलती औसत, यह समापन मूल्य पर चलती विंडो फ़ंक्शन के प्रत्येक मूल्य का औसत है

function sma($close, window) { return rolling(x => mean(x), window, $close); }

जहां माध्य () फ़ंक्शन औसत मान है, विंडो पैरामीटर विंडो का आकार है, और रोलिंग () विंडो फ़ंक्शन का एक संयोजन है, जो कि सरणी में प्रत्येक वर्तमान सेल के लिए अंतिम n तत्वों की एक सरणी का उत्पादन करता है, और ऑपरेशन जो विंडो को एक संख्या तक कम करता है।

 function rolling(operation, window, array) { let result = []; for (let i = 0; i < array.length; i++) { if (i + 1 < window) { result.push(NaN); } else { result.push(operation(array.slice(i + 1 - window, i + 1))); } } return result; }

मूविंग एवरेज लैगिंग इंडिकेटर है और ट्रेंड को निर्धारित करने में मदद करता है। यह मूल्य चार्ट के शीर्ष पर उपरिशायी है और पहले मूल्यों को आमतौर पर त्याग दिया जाता है।

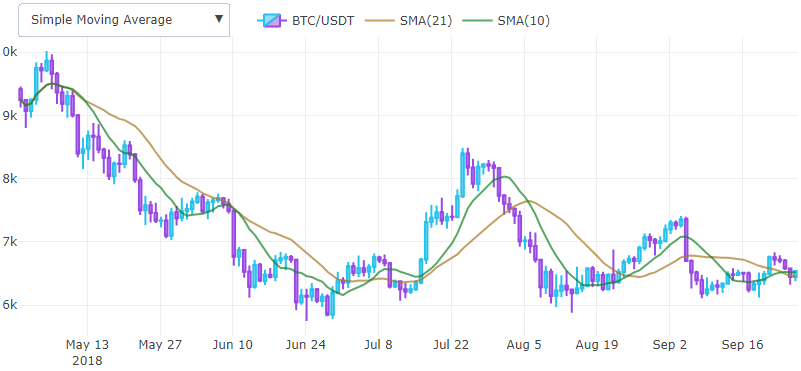
मूविंग एवरेज (SMA)

आमतौर पर, संकेतकों की एक जोड़ी को माना जाता है, और बिंदु जब छोटी खिड़की के साथ एक संकेतक एक लंबी खिड़की के साथ एक संकेतक को पार करता है, नीचे से एक संभावित प्रवेश बिंदु और ऊपर से एक निकास बिंदु माना जाता है। व्यवहार में, देरी प्रभाव को कम करने के लिए एक भारित विंडो फ़ंक्शन का उपयोग करते हुए, एक घातीय भारित चलती औसत अधिक बार उपयोग किया जाता है।

मानक विचलन (STDEV)

यदि हम पिछले संस्करण में माध्य () फ़ंक्शन को रूट के साथ विचरण sd () से प्रतिस्थापित करते हैं, तो हमें एक गतिमान विचलन मिलेगा।

 function stdev($close, window) { return rolling(x => sd(x), window, $close); }

फैलाव सामान्य रूप से सामान्य माना जाता है, सबसे अधिक बार बेसेल सुधार के बिना। विचरण की जड़ का भी उपयोग किया जाता है, क्योंकि विचरण को वर्गाकार रूबल / डॉलर में मापा जाता है।

बोलिंगर बैंड (बीबी)

इस प्रकार, हम पहले से ही दो बुनियादी संकेतक प्राप्त कर चुके हैं जो पहले से ही संयुक्त हो सकते हैं और नए प्राप्त कर सकते हैं। उदाहरण के लिए, यदि हम बिंदु को जोड़कर चलते औसत और मानक विचलन को 2 से गुणा करते हैं, तो हमें बोलिंगर बैंड का ऊपरी भाग मिलता है, और अगर हम निचले हिस्से को घटाते हैं।

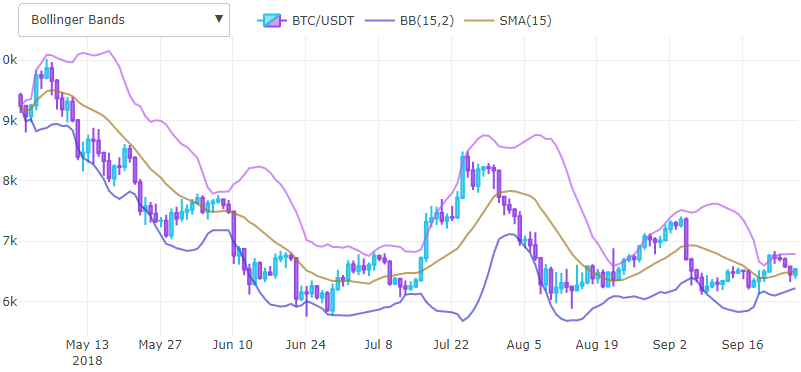
बोलिंगर बैंड (बीबी)

कोड में, यह इस तरह दिखेगा

 function bb($close, window, mult) { let middle = sma($close, window); let upper = pointwise((a, b) => a + b * mult, middle, stdev($close, window)); let lower = pointwise((a, b) => a - b * mult, middle, stdev($close, window)); return { lower : lower, upper : upper}; }

जहाँ पॉइंटवाइज़ फंक्शन कुछ और नहीं करता है, लेकिन इसे दिए गए ऑपरेशन का उपयोग करके दो सरणियों से एक तत्व एकत्र करता है।

बोलिंगर बैंड एक बड़े मूल्य आंदोलन से पहले लुल्ल को निर्धारित करने में मदद करते हैं, और एक चार्ट पर सुविधाजनक रूप से वोल्टैट प्रदर्शित करने के लिए एक उपकरण के रूप में उपयोग किया जाता है, मानक विचलन को उसी चार्ट पर ओवरले के रूप में मूल्य के रूप में प्रदर्शित नहीं किया जा सकता है, इसलिए इसे चलती औसत से स्थगित करना सुविधाजनक है।

टिप्पणी

इस सूचक में एक खामी है - यह घातीय कार्यों का उपयोग करता है। एक अभ्यास के रूप में, आप इसे स्वयं को बदलने की कोशिश कर सकते हैं, यह ध्यान रखना न भूलें कि मानक विचलन को भी तेजी से संतुलित गणना करने की आवश्यकता है।

घातीय मूविंग एवरेज (ईएमए)

चलती औसत अंतराल को कैसे कम किया जा सकता है? इसकी गणना करते समय, एन अंतिम समापन कीमतों को जोड़ा जाता है, आप समझ सकते हैं कि आप कुछ वजन के साथ जोड़ सकते हैं, पुरानी कीमतों के योगदान को कम कर सकते हैं। इस प्रकार हम एक भारित विंडो फ़ंक्शन के सूत्र पर आते हैं।

\ bar x = \ frac {\ sum x_i} {N} = \ frac {\ _ 1 \ _ cdot x_i} {\ sum 1} \ quad \ Rightarrow \ quad \ widetilde {x} = \ _rac {\ sum x_i w_i } {\ _ w_i}

$\ bar x = \ frac {\ sum x_i} {N} = \ frac {\ _ 1 \ _ cdot x_i} {\ sum 1} \ quad \ Rightarrow \ quad \ widetilde {x} = \ _rac {\ sum x_i w_i } {\ _ w_i}$

अगर

$w_i = q ^ i$ और किसी प्रकार का स्थिरांक चुनें

$q$ एक से कम है, तो हम एक असीम रूप से कम वजन प्राप्त करते हैं, अगर एक ही समय में नवीनतम से शुरू होने वाली कीमतों को जोड़ दें।

वजन कार्यों

यदि पूंछ योगदान को ध्यान में नहीं रखा जाता है, तो गणना को बहुत सरल बनाया जा सकता है। खिड़की के आकार को पूरी लंबाई तक विस्तारित करके, आप एक पुनरावर्ती परिभाषा प्राप्त कर सकते हैं।

$1 + q + q ^ 2 + ... + q ^ n \ underset {n \ to \ infty} {\ underset {q <0} {\ approx}} \ frac {1} {1-q} \\ \ mathrm {EMA} _ {curr} = \ frac {\ sum x_i q ^ i} {\ sum q ^ i} \ लगभग (1-q) \ sum x_i q ^ i \\ \ mathrm [EMA} _ {अगला } = \ frac {x_ {अगला} + q \ cdot \ sum x_i q ^ i} {1 + q \ cdot \ sum q ^ i} = = (1-q) \ cdot \ left [x_ {अगला} + \ _o cdot \ sum x_i q ^ i \ right] \\ \ mathrm {EMA} _ {अगला} = (1-q) \ cdot x_ {अगला} + q \ cdot \ mathrm {EMA} _ [वक्र}$

नतीजतन, हमें कुछ मूल्य चुनने की आवश्यकता है

$\ अल्फा = 1-q$ एक चौरसाई स्थिरांक के रूप में। यह दिखाया जा सकता है कि यदि आप लेते हैं

$\ अल्फा = 2 / (एन + 1)$ ऊपर ईएमए और एसएमए भार के द्रव्यमान का केंद्र समान हो जाता है। कोड में, यह सब बहुत आसान लग रहा है।

 function ema($close, window, weight = null) { weight = weight ? weight : 2 / (window + 1); let ema = [ mean($close.slice(0, window)) ]; for (let i = 1; i < $close.length; i++) { ema.push($close[i] * weight + ema[i - 1] * (1 - weight)); }; return ema; }

सामान्य तौर पर, यह एक ही चलती औसत है, लेकिन अधिक संवेदनशील है।

घातीय मूविंग एवरेज (ईएमए)

उपयोग की क्षमता आपके अनुभव और उपयोग की गई सेटिंग्स पर निर्भर करती है। उदाहरण के लिए, इस साइट पर पैरामीटर बहुत अच्छी तरह से चुने गए हैं।

मूविंग एवरेज कन्वर्जेंस / डाइवर्जेंस (एमएसीडी)

1979 में जेराल्ड अपेल एक सबसे सरल और एक ही समय में मूल्य बिंदुओं के प्रभावी दोलक के साथ आया। यह दो ईएमए ट्रेंड इंडिकेटर्स को एक पल इंडिकेटर में परिवर्तित करता है, दो दुनियाओं से सर्वश्रेष्ठ लेता है। यही है, वह, मोटे तौर पर बोलता है, एक व्युत्पन्न पाता है। यह दो पंक्तियों और एक हिस्टोग्राम के साथ एक अलग विंडो में तैयार किया गया है, और पिछले वाले के रूप में ओवरले नहीं। वास्तव में, बहुत अधिक संकेतक हैं जो एक अलग विंडो में तैयार किए गए हैं, लेकिन यह कुछ अन्य समय के बारे में हो सकता है।

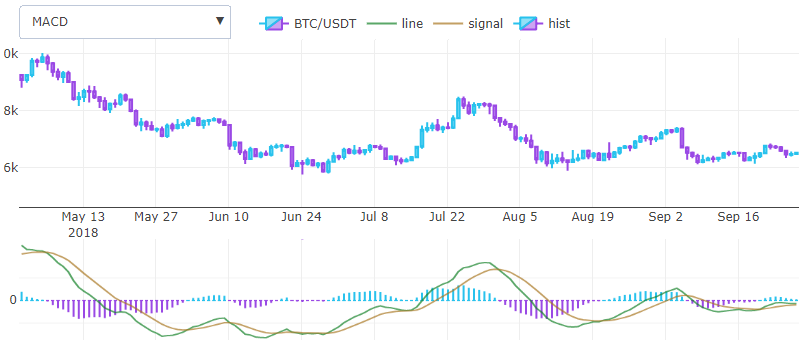
मूविंग एवरेज कन्वर्जेंस / डाइवर्जेंस (एमएसीडी)

मूविंग एवरेज कन्वर्जेंस / डाइवर्जेंस (एमएसीडी)

गणना सूत्र काफी सरल है, एक छोटी और छोटी खिड़की के साथ दो ईएमए लें, उदाहरण के लिए, 26 और 12 इकाइयां, और घटाया, जिसके परिणामस्वरूप लाइन वांछित संकेतक होगी। 3 इकाइयों के एक चरण के साथ इस अंतर से एक और ईएमए लेते हुए, हम एक सिग्नल लाइन प्राप्त करते हैं। बाद में गेराल्ड जोड़ा गया हिस्टोग्राम की गणना दो पिछले परिणामों के बीच के अंतर से की जाती है और अनिवार्य रूप से एक भारित औसत व्युत्पन्न है।

 function macd($close, wshort, wlong, wsig) { let line = pointwise((a, b) => a - b, ema($close, wshort), ema($close, wlong)); let signal = ema(line, wsig); let hist = pointwise((a, b) => a - b, line, signal); return { line : line, signal : signal, hist : hist }; }

संकेतक परीक्षण, सामान्यीकृत मानक त्रुटि

संकेतकों के अर्थ के साथ सटीक तालिकाओं के साथ, आप गुणात्मक रूप से अपनी गणना का परीक्षण कर सकते हैं। दो कार्यों के बीच त्रुटि के माप को निर्धारित करने के विभिन्न तरीके हैं, लेकिन अभ्यास से पता चला है कि सामान्यीकृत माध्य वर्ग त्रुटि, जिसे माना जाता है

$\ mathrm {NRMSE} = \ left। \ sqrt {\ frac {\ _ sum (\ hat x_i - x_i) ^ 2} {N}} \ Middle / (\ max {x_i} - \ min {x_i}) \ _ $$

छोटे और बड़े दोनों आकारों के लिए सबसे अच्छा काम करता है। उदाहरण के लिए, डॉलर में बिटकॉइन की कीमत 20,000 डॉलर हो सकती है और $ 10 का अंतर महत्वपूर्ण नहीं है, एक ही समय में, एक altcoin की गणना कई सातोशी में की जा सकती है।

 function nrmse(f, g) { let sqrDiff = pointwise((a, b) => (a - b) * (a - b), f, g); return Math.sqrt(mean(sqrDiff)) / (Math.max(...f) - Math.min(...f)); }

निष्कर्ष

इसलिए कुछ पंक्तियों में आप बुनियादी संकेतकों को व्यक्त कर सकते हैं, यदि आप मशीन लर्निंग द्वारा उनके विश्लेषण को पूरा करने की योजना बनाते हैं, तो आदर्श प्रवेश बिंदुओं को निर्धारित करने के लिए, मैं आपको ज़िगज़ैग संकेतक पर ध्यान देने की सलाह देता हूं, जो कि व्यापार के लिए उपयोगी नहीं है, लेकिन शिक्षक के रूप में बेहद उपयोगी है। यह भी ध्यान में रखा जाना चाहिए कि व्यापार के लिए आपको सबसे अलग संकेतक चुनने और उनके इनपुट मापदंडों को बदलने की कोशिश करने की आवश्यकता है। आप समय के साथ उन्हें स्वचालित रूप से बदलने की कोशिश कर सकते हैं, क्योंकि सबसे प्रभावी पैरामीटर बदलते हैं।

सूत्रों का उपयोग किया

1. स्टॉकचार्ट्स - तालिकाओं में सत्यापन डेटा के साथ एल्गोरिदम की सूची
2. क्रिप्टोवैच - अच्छी तरह से ट्यून किए गए संकेतक पैरामीटर
3. गितुब - स्रोत कोड

शेयर बाजारों में तकनीकी संकेतक कैसे हैं

More articles: