👨🏼‍🚒 🚵🏼 🥦 Nonlinear समीकरणों के सिस्टम को हल करने के लिए संख्यात्मक तरीके 😌 🈸 🐄

परिचय

कई लागू समस्याओं में एक गैर-समीकरण समीकरणों की प्रणाली के लिए एक सामान्य समाधान खोजने की आवश्यकता होती है। Nonlinear समीकरणों की प्रणाली का कोई सामान्य विश्लेषणात्मक समाधान नहीं मिला। केवल संख्यात्मक तरीके हैं।

यह एक दिलचस्प तथ्य है कि वास्तविक संख्याओं पर समीकरणों की किसी भी प्रणाली को एक समान समीकरण द्वारा दर्शाया जा सकता है, यदि हम फॉर्म में सभी समीकरणों को लेते हैं

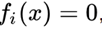
, उन्हें वर्ग और उन्हें मोड़ो।

संख्यात्मक समाधान के लिए, विभिन्न संशोधनों में क्रमिक सन्निकटन (सरल पुनरावृत्ति) और न्यूटन की विधि के पुनरावृत्त तरीकों का उपयोग किया जाता है। सूत्र के गैर-समीकरण समीकरणों की एक प्रणाली के मामले में स्वाभाविक रूप से Iterative प्रक्रियाओं को सामान्यीकृत किया जाता है:

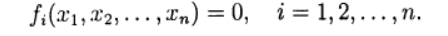
(1)

द्वारा निरूपित करें

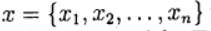
अज्ञात के वेक्टर और एक वेक्टर फ़ंक्शन को परिभाषित करते हैं

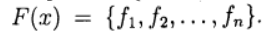
तब सिस्टम (1) समीकरण के रूप में लिखा जाता है:

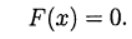
(2)

अब, अपने प्यारे पायथन पर लौटते हैं और प्रोग्रामिंग भाषाओं के बीच इसकी प्रधानता पर ध्यान देते हैं जो सीखना चाहते हैं [1]।

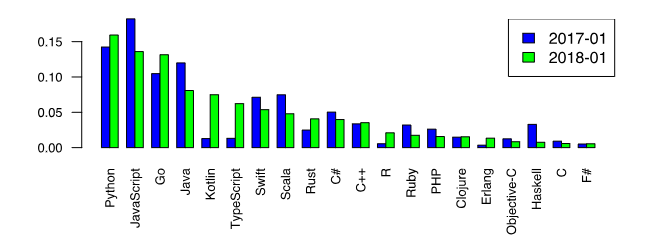
यह तथ्य पायथन में संख्यात्मक तरीकों पर विचार करने के लिए एक अतिरिक्त प्रोत्साहन है। हालांकि, पायथन प्रेमियों के बीच एक राय है कि विशेष पुस्तकालय कार्य, जैसे कि scipy.optimize.root, spsolve_trianular, newton_krylov , संख्यात्मक विधियों द्वारा समस्याओं को हल करने के लिए सबसे अच्छा विकल्प हैं।

इससे असहमत होना मुश्किल है, यदि केवल इसलिए कि विभिन्न प्रकार के मॉड्यूल ने भी पायथन को लोकप्रियता के शिखर पर पहुंचा दिया है। हालांकि, ऐसे मामले भी हैं, जब एक सरसरी परीक्षा के साथ, विज्ञानपी लाइब्रेरी के विशेष कार्यों का उपयोग किए बिना प्रत्यक्ष ज्ञात विधियों का उपयोग करना भी अच्छे परिणाम देता है। दूसरे शब्दों में, नया अच्छी तरह से भूल गया पुराना है।

इसलिए, प्रकाशन [2] में, कम्प्यूटेशनल प्रयोगों के आधार पर, यह साबित हो गया था कि लाइब्रेरी फ़ंक्शन न्यूटन_क्रायलोव, जिन्हें गैर-रेखीय समीकरणों की बड़ी प्रणालियों को हल करने के लिए डिज़ाइन किया गया है, की TSLS + WD एल्गोरिथ्म की तुलना में आधी गति है।
(दो कदम कम से कम वर्गों) NumPy पुस्तकालय द्वारा कार्यान्वित किया गया।

इस प्रकाशन का उद्देश्य पुनरावृत्तियों की संख्या, गति और सबसे महत्वपूर्ण रूप से तुलना करना है, एक सौ nonlinear बीजीय समीकरणों की एक प्रणाली के रूप में हल करने का परिणाम है scipy.optimize.rogr पुस्तकालय फ़ंक्शन और न्यूटन विधि का उपयोग करके न्यूपे लाइब्रेरी का उपयोग करके लागू किया गया।

बीजगणितीय nonlinear समीकरणों के संख्यात्मक रूप से हल करने वाली प्रणालियों के लिए Scipy.optimize.root solver क्षमताएं

लाइब्रेरी फ़ंक्शन scipy.optimize.root को तुलनात्मक आधार के रूप में चुना गया था क्योंकि इसमें तुलनात्मक विश्लेषण के लिए उपयुक्त तरीकों की एक विस्तृत लाइब्रेरी है।

scipy.optimize.root ( मज़ा, x0, args = (), विधि = 'संकर', jac = कोई नहीं, tol = कोई नहीं, कॉलबैक = कोई नहीं, ptions = कोई नहीं )
मज़ा - रूट खोजने के लिए एक वेक्टर फ़ंक्शन।
जड़ों को खोजने के लिए x0 -Initial शर्तें

विधि:
संकर - संकर विधि के पावेल संशोधन का उपयोग किया जाता है;
एलएम - कम से कम वर्गों की विधि का उपयोग करके गैर-समीकरणों की प्रणालियों को हल करता है।
प्रलेखन [3] से निम्नानुसार, तरीके broyden1, broyden2, anderson, linearmixing, diagbroyden, रोमांचक, krylov न्यूटन के सटीक तरीके हैं। शेष पैरामीटर "वैकल्पिक" हैं और दस्तावेज में पाए जा सकते हैं।

Nonlinear समीकरणों के सिस्टम को हल करने के तरीके

नीचे दी गई सामग्री को वास्तव में साहित्य में पढ़ा जा सकता है, उदाहरण के लिए, [4] में, लेकिन मैं अपने पाठक का सम्मान करता हूं और, उसकी सुविधा के लिए, यदि संभव हो तो विधि की व्युत्पत्ति एक संक्षिप्त रूप में प्रस्तुत करता हूं। जिन लोगों को सूत्र पसंद नहीं हैं वे इस अनुभाग को छोड़ देते हैं।

न्यूटन की विधि में, समीकरणों की प्रणाली को हल करने के लिए एक नया अनुमान (2) रैखिक समीकरणों की प्रणाली के समाधान से निर्धारित किया जाता है :

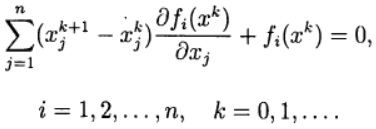
(3)

जैकोबी मैट्रिक्स को परिभाषित करें:

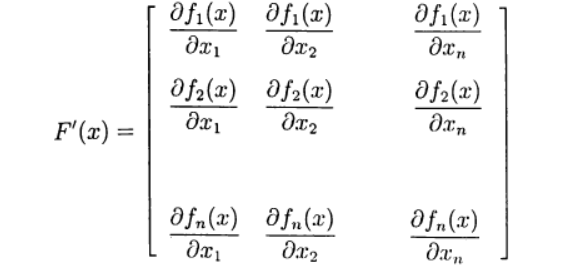
(4)

हम फॉर्म में लिखते हैं:

(5)

रेखीय बीजगणितीय समीकरणों के सिस्टम को हल करने के लिए दो-परत पुनरावृत्ति विधियों के साथ (2) के अनुमानित समाधान के लिए कई एक-चरण विधियाँ फार्म में लिखी जा सकती हैं:

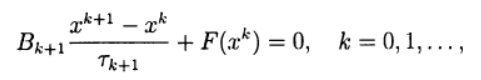
(6)

जहाँ

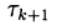
क्या पुनरावृत्त पैरामीटर, ए

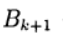
- व्युत्क्रम होने वाला एक वर्ग मैट्रिक्स n x n।

रिकॉर्ड का उपयोग करते समय (6), न्यूटन की विधि (5) पसंद से मेल खाती है:

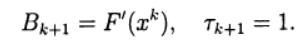
एक नया अनुमान लगाने के लिए रैखिक समीकरणों की प्रणाली (5)

इसे हल किया जा सकता है। इस मामले में, हमारे पास बाहरी और आंतरिक पुनरावृत्तियों के साथ दो-चरण पुनरावृत्ति प्रक्रिया है। उदाहरण के लिए, न्यूटन पद्धति के अनुसार एक बाहरी पुनरावृत्ति प्रक्रिया को अंजाम दिया जा सकता है, और आंतरिक पुनरावृत्तियों को सेडेल पुनरावृत्ति विधि के आधार पर किया जा सकता है ।

नॉनलाइनियर समीकरणों के सिस्टम को हल करते समय, कोई मानक पुनरावृत्तियों के प्रत्यक्ष एनालॉग्स का उपयोग कर सकता है जो कि रैखिक समीकरणों की प्रणालियों को हल करने के लिए उपयोग किया जाता है। समाधान के लिए लागू गैर-रेखीय सेडेल विधि (2) देता है:

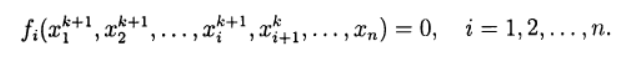
(7)

इस मामले में, गैर-समीकरण के समाधान से नए सन्निकटन के प्रत्येक घटक को विभिन्न संशोधनों में सरल पुनरावृत्ति विधि और न्यूटन की विधि के आधार पर प्राप्त किया जा सकता है। इस प्रकार, हम फिर से एक दो-चरण पुनरावृत्त विधि के लिए आते हैं जिसमें बाह्य पुनरावृत्तियों को सीडेल विधि के अनुसार किया जाता है, और आंतरिक पुनरावृत्तियों को न्यूटन विधि का उपयोग करके किया जाता है।

गैर-समीकरणों की प्रणालियों के अनुमानित समाधान के लिए न्यूटन विधि को लागू करने में मुख्य कम्प्यूटेशनल कठिनाइयाँ प्रत्येक पुनरावृत्ति पर एक जैकोबी मैट्रिक्स के साथ समीकरणों के एक रैखिक प्रणाली को हल करने की आवश्यकता से संबंधित हैं , और यह मैट्रिक्स पुनरावृत्ति से पुनरावृत्ति में बदल जाती है। संशोधित न्यूटन विधि में, जैकोबी मैट्रिक्स केवल एक बार उल्टा होता है:

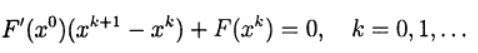
(8)

मॉडल समारोह चयन

इस तरह का चुनाव एक सरल काम नहीं है, क्योंकि चर की संख्या में वृद्धि के अनुसार प्रणाली में समीकरणों की संख्या में वृद्धि के साथ, समाधान का परिणाम नहीं बदलना चाहिए, क्योंकि दो तरीकों की तुलना करते समय समीकरणों के प्रणाली के समाधान की शुद्धता को ट्रैक करना असंभव है। मैं मॉडल फ़ंक्शन के लिए निम्नलिखित समाधान लाता हूं:

n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f

फंक्शन f, n nonlinear समीकरणों की एक प्रणाली बनाता है, जिसका समाधान समीकरणों की संख्या पर निर्भर नहीं करता है और प्रत्येक n चर के लिए एकता के बराबर है।

लाइब्रेरी फ़ंक्शन ऑप्टिमाइज़ेशन का उपयोग करके बीजीय नॉनलाइन समीकरणों की एक प्रणाली को हल करने के परिणामों के साथ एक मॉडल फ़ंक्शन पर परीक्षण के लिए एक कार्यक्रम। जड़ों को खोजने के विभिन्न तरीकों के लिए।

 from numpy import* from scipy import optimize import time ti = time.clock() n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) sol = optimize.root(f,x0, method='krylov') print('Solution:\n', sol.x) print('Krylov method iteration = ',sol.nit) print('Optimize root time', round(time.clock()-ti,3), 'seconds')

प्रलेखन में दिए गए तरीकों में से केवल एक [3] ने एक मॉडल फ़ंक्शन को हल करने के परीक्षण पर पारित किया, यह 'क्रायलोव' विधि है ।

एन = 100 के लिए समाधान:

समाधान:
[1। 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1.]
क्रायलोव विधि पुनरावृत्ति = 4219
रूट समय 7.239 सेकंड का अनुकूलन करें:

एन = 200 के लिए समाधान

समाधान:
[1.00000018 0.99999972 0.99999985 1.00000001 0.99999992 1.00000049
0.99999998 0.99999992 0.99999991 1.00000001 1.00000013 1.00000002
0.9999997 0.99999987 1.00000005 0.99999978 1.0000002 1.00000012
1.00000023 1.00000017 0.99999979 1.00000012 1.00000026 0.99999987
1.00000014 0.99999979 0.99999988 1.00000046 1.00000064 1.00000007
1.00000049 1.00000005 1.00000032 1.00000031 1.00000028 0.99999992
1.0000003 1.0000001 0.99999971 1.00000023 1.00000039 1.0000003
1.00000013 0.9999999 0.99999993 0.99999996 1.00000008 1.00000016
1.00000034 1.00000004 0.99999993 0.99999987 0.99999969 0.99999985
0.99999981 1.00000051 1.0000004 1.00000035 0.9999998 1.00000065
1.00000061 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.00000059 1.00000056
1.00000047 1.00000016 1.00000018 0.99999988 1.00000061 1.00000002
1.00000033 1.00000034 1.0000004 1.00000046 1.00000009 1.00000024
1.00000017 1.00000014 1.00000054 1.00000006 0.99999964 0.99999968
1.00000005 1.00000049 1.0000005 1.00000028 1.00000029 1.00000027
1.00000027 0.9999998 1.00000005 0.99999974 0.99999978 0.99999988
1.00000015 1.00000007 1.00000005 0.99999973 1.00000006 0.99999995
1.00000021 1.00000031 1.00000058 1.00000023 1.00000023 1.00000044
0.99999985 0.99999948 0.99999977 0.99999991 0.99999974 0.99999978
0.99999983 1.0000002 1.00000016 1.00000008 1.00000013 1.00000007
0.99999989 0.99999959 1.00000029 1.0000003 0.99999972 1.00000003
0.99999967 0.99999977 1.00000017 1.00000005 1.00000029 1.00000034
0.99999997 0.99999989 0.99999945 0.99999985 0.99999994 0.99999972
1.00000029 1.00000016]
क्रायलोव विधि पुनरावृत्ति = 9178
रूट समय 23.397 सेकंड का अनुकूलन करें

निष्कर्ष: दो के एक कारक द्वारा समीकरणों की संख्या में वृद्धि के साथ, समाधान में त्रुटियों की उपस्थिति ध्यान देने योग्य है। एन में एक और वृद्धि के साथ, समाधान अस्वीकार्य हो जाता है, जो कदम के लिए स्वत: अनुकूलन के कारण संभव है, प्रदर्शन में तेज गिरावट का एक ही कारण है। लेकिन यह सिर्फ मेरा अनुमान है।

संशोधित किए गए न्यूटन विधि का उपयोग करके जड़ों को खोजने के लिए पायथन 3 में लिखे गए प्रोग्राम (1) - (8) का उपयोग करते हुए पायथन 3 में लिखे गए प्रोग्राम का उपयोग करके बीजीय नॉनलाइन समीकरणों की एक प्रणाली को हल करने के परिणामों के साथ एक मॉडल फ़ंक्शन के लिए एक कार्यक्रम।

संशोधित न्यूटन विधि के अनुसार जड़ों को खोजने का कार्यक्रम

 from numpy import* import time ti = time.clock() def jacobian(f, x): h = 1.0e-4 n = len(x) Jac = zeros([n,n]) f0 = f(x) for i in arange(0,n,1): tt = x[i] x[i] = tt + h f1= f(x) x[i] = tt Jac [:,i] = (f1 - f0)/h return Jac, f0 def newton(f, x, tol=1.0e-9): iterMax = 50 for i in range(iterMax): Jac, fO = jacobian(f, x) if sqrt(dot(fO, fO) / len(x)) < tol: return x, i dx = linalg.solve(Jac, fO) x = x - dx print ("Too many iterations for the Newton method") n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) x, iter = newton(f, x0) print ('Solution:\n', x) print ('Newton iteration = ', iter) print('Newton method time', round(time.clock()-ti,3), 'seconds')

एन = 100 के लिए समाधान:

समाधान:
[1। 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1.]
न्यूटन पुनरावृत्ति = 13
न्यूटन विधि समय 0.496 सेकंड

एन = 200 के लिए समाधान:

समाधान:
[1। 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1.]
न्यूटन पुनरावृत्ति = 14
न्यूटन विधि समय 1.869 सेकंड

यह सुनिश्चित करने के लिए कि प्रोग्राम वास्तव में सिस्टम को हल करता है, हम फॉर्म में 1 के मान के साथ रूट से बचने के लिए मॉडल फ़ंक्शन को फिर से लिखते हैं:

 n=10 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i]*sin([i]) - x[i-1] - 2*x[i+1] - 2+e**-x[i] f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f

हमें मिलता है:
समाधान:
[0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49362062
-1.31649896 0.6865098 0.89609091 0.98509235]
न्यूटन पुनरावृति = 16
न्यूटन विधि समय 0.046 सेकंड

निष्कर्ष: जब मॉडल फ़ंक्शन बदलता है तो प्रोग्राम भी काम करता है।

अब हम प्रारंभिक मॉडल फ़ंक्शन पर लौटते हैं और n के लिए एक व्यापक श्रेणी की जांच करते हैं, उदाहरण के लिए, 2 और 500 पर।
n = 2
समाधान:
[1। 1.]
न्यूटन पुनरावृत्ति = 6
न्यूटन विधि समय 0.048 सेकंड
n = 500

n = 500

समाधान:
[1। 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1।
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
न्यूटन पुनरावृति = 15
न्यूटन विधि समय 11.754 सेकंड

निष्कर्ष:

पाइथन में लिखा गया एक कार्यक्रम संशोधित न्यूटन विधि का उपयोग करते हुए, दिए गए मॉडल फ़ंक्शन से गैर-समांतर समीकरणों की प्रणालियों को हल करते समय, लाइब्रेरी फ़ंक्शन ऑप्टिमाइज़ेशन का उपयोग करते समय समाधान की तुलना में अधिक स्थिरता होती है। क्रायलोव विधि के लिए fot.root (f, x0, method = 'kallolov) का उपयोग करते हुए। अंतिम निष्कर्ष की गति के बारे में, चरण नियंत्रण के लिए अलग-अलग दृष्टिकोण के कारण आकर्षित करना असंभव है।

संदर्भ:

प्रोग्रामिंग भाषाओं की रेटिंग 2018।
कूपर आई.वी., फेलिकिक बी.वी. गैर-मैट्रिक्स समीकरण की बड़ी प्रणालियों के लिए रूट माध्य वर्ग त्रुटि दमन के साथ गैर-मैट्रिक्स पुनरावृत्ति प्रक्रियाएं।
scipy.optimize.root।
वाबिशचेविच पी.एन. संख्यात्मक तरीके: कम्प्यूटेशनल कार्यशाला। - एम .: बुक हाउस "लिब्रोकॉम", 2010. - 320 पी।

Nonlinear समीकरणों के सिस्टम को हल करने के लिए संख्यात्मक तरीके

परिचय

बीजगणितीय nonlinear समीकरणों के संख्यात्मक रूप से हल करने वाली प्रणालियों के लिए Scipy.optimize.root solver क्षमताएं

Nonlinear समीकरणों के सिस्टम को हल करने के तरीके

मॉडल समारोह चयन

निष्कर्ष:

More articles: