पायथन का उपयोग करके आकाशीय पिंडों की कक्षाओं का निर्माण

कक्षा निर्धारण के लिए संदर्भ प्रणाली

शास्त्रीय यांत्रिकी में सापेक्ष गतियों के प्रक्षेपवक्र को खोजने के लिए, सभी संदर्भ फ्रेम (जड़ता और गैर-जड़ता) दोनों में पूर्ण समय की धारणा का उपयोग किया जाता है।

इस धारणा का उपयोग करते हुए, हम दो अलग-अलग संदर्भ फ़्रेमों में एक ही बिंदु की गति पर विचार करते हैं $$$K$ और $$$K ^ {'}$ जिनमें से दूसरी मनमानी गति से पहली के सापेक्ष चलती है $$$\ vec {V (t)} = \ dot {\ vec {R (t)}}$ जहाँ $$$\ vec {R (t)}$ त्रिज्या वेक्टर समन्वय प्रणाली की उत्पत्ति की स्थिति का वर्णन करता है $$$K ^ {'}$ संदर्भ के फ्रेम के सापेक्ष $$$K$ )।

हम सिस्टम में एक बिंदु की गति का वर्णन करेंगे $$$K ^ {'}$ त्रिज्या वेक्टर $$$\ vec {r ^ {'}} (t)$ प्रणाली की उत्पत्ति से निर्देशित $$$K ^ {'}$ बिंदु की वर्तमान स्थिति के लिए। फिर संदर्भ फ्रेम के सापेक्ष विचाराधीन बिंदु की गति $$$K$ एक त्रिज्या वेक्टर द्वारा वर्णित है $$$\ vec {r (t)}$ :

$$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ , (1)

और सापेक्ष गति $$$\ vec {v (t)}$

$$$\ vec {v} (t) = \ dot {\ vec {r ^ {'}}} (t) + \ dot {\ vec {R}} (t)$ , (2)

जहाँ $$$\ _ {\ vec {r ^ {'}}} (t)$ - सिस्टम के सापेक्ष बिंदु की गति $$$K ^ {'}$ ; $$$\ _ {\ vec {R}} (t)$ -फ्रेम स्पीड $$$K ^ {'}$ संदर्भ के फ्रेम के सापेक्ष $$$K$ ।



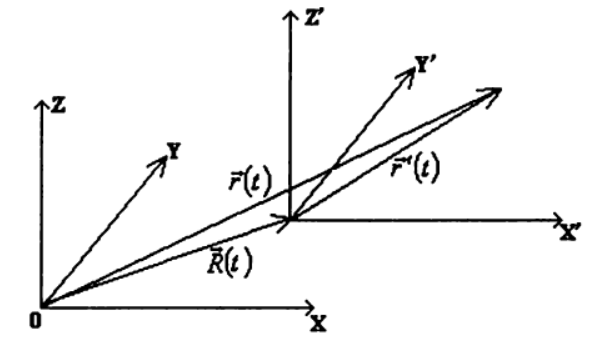
इस प्रकार, एक मनमाना संदर्भ फ्रेम में एक बिंदु की गति के कानून को खोजने के लिए $$$K$ आपको:

1) बिंदु की गति का नियम निर्धारित करें - $$$\ vec {r ^ {'}} (t)$ संदर्भ के फ्रेम के सापेक्ष $$$K ^ {'}$ ;
2) गति का नियम निर्धारित करें - $$$\ vec {R} (t)$ संदर्भ प्रणाली $$$K ^ {'}$ संदर्भ के फ्रेम के सापेक्ष $$$K$
3) बिंदु की गति का नियम निर्धारित करें - $$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ संदर्भ के फ्रेम के सापेक्ष $$$K$ ।

हेलियोसेंट्रिक संदर्भ फ्रेम में चंद्रमा की कक्षा का निर्माण

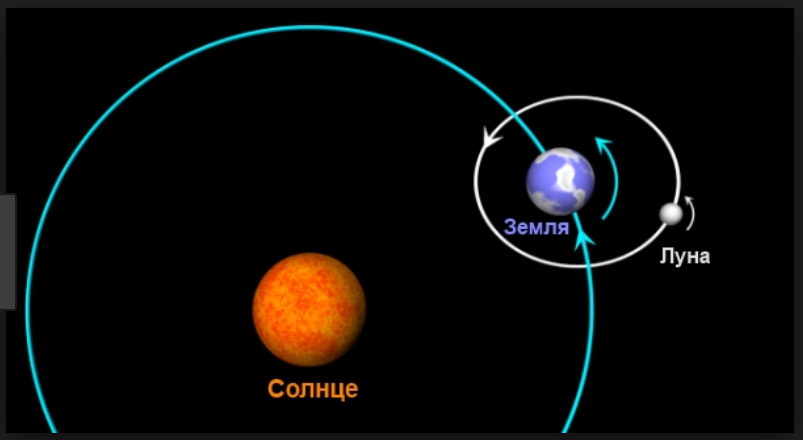हेलियोसेन्ट्रिक संदर्भ प्रणाली (सिस्टम) में $$$K$ ) पृथ्वी त्रिज्या के एक चक्र में घूमती है
$$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ किमी (परिसंचरण अवधि) $$$T_ {1} = 3,156 \ cdot 10 ^ {7}$ रों।)। चंद्रमा, बदले में, त्रिज्या के एक चक्र के चारों ओर पृथ्वी (सिस्टम K ') के चारों ओर घूमता है $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ किमी। (परिसंचरण अवधि $$$T_ {2} = 2.36 \ cdot 10 ^ {6}$ एक। जैसा कि ज्ञात है [1,2], जब कोई पदार्थ बिंदु त्रिज्या के एक वृत्त के साथ चलता है $$$आर$ निरंतर कोणीय वेग के साथ $$$\ _ ओमेगा$ नियम के अनुसार बिंदु परिवर्तन की वर्तमान स्थिति के लिए मूल से तैयार त्रिज्या वेक्टर के निर्देशांक:

$$

$$\ vec {R (t)} = \ binom {R \ cdot cos (\ omega \ cdot t + \ varphi _ {0})} {R \ cdot sin (\ omega \ cdot t + varphi _ {0})}} = \ binom {R \ cdot cos (\ frac {2 \ pi} {T}) + \ varphi _ {0})} {R \ cdot sin (\ frac {2 \ pi} {T} + varphi _ { 0})}, (3)$$

जहाँ $$$\ varphi _ {0}$ - प्रारंभिक चरण समय पर कण की स्थिति को दर्शाता है $$$t = 0$ , जो भविष्य में हम शून्य के बराबर मान लेंगे। में जगह (3) $$$आर$ पर $$$R_ {1}$ और $$$R_ {2}$ और (1) में प्रतिस्थापित करते हुए, हम समय पर हेलियोसेंट्रिक समन्वय प्रणाली में चंद्रमा की त्रिज्या वेक्टर की निर्भरता प्राप्त करते हैं:

$$

$$\ vec {r (t)} = \ binom {x (t)} {y (t)} = \ binom {R_ {2} cos (\ frac {2 \ pi} {T_ {2}} t +) R_ {1} cos (\ frac {2 \ pi} {T_ {1}} t)} {R_ {2} पाप (\ frac {2 \ pi} {T_ {2}} t) + R_ {{}} पाप ((frac {2 \ pi} {T_ {1}} t)}, (4)$$

अभिव्यक्ति (4) चंद्रमा की कक्षा निर्धारित करती है ( $$$y = y (x (t))$ ) पैरामीट्रिक रूप में, जहां पैरामीटर समय है। पायथन का उपयोग करके वांछित कक्षा का निर्माण करने के लिए, हम कक्षाओं की त्रिज्या और पृथ्वी और चंद्रमा की रोटेशन अवधि निर्धारित करते हैं।

पृथ्वी एक सहायक प्रणाली में चलती है ( $$$K$ ) इसकी कक्षा त्रिज्या और क्रांति की अवधि क्रमशः बराबर है $$$R_ {1} = 1.496 \ cdot 10 ^ {8} किमी, T_ {1} = 3.156 \ cdot 10 ^ {7} s$ एक समन्वय प्रणाली में चंद्रमा पृथ्वी के चारों ओर घूमता है ( $$$K ^ {'}$ ) इसकी कक्षा त्रिज्या और क्रांति की अवधि क्रमशः बराबर है $$$R_ {2} = 3.844 \ cdot 10 ^ {5} किमी, T_ {2} = 2.36 \ cdot 10 ^ {6}$ ।

(4) को देखते हुए, हम समय पर निर्देशांक की निर्भरता के कार्यों को निर्धारित करते हैं:

$$

$$\ binom {(X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} \ cdot t), Y (t) = R_ {1} \ cdot sin (\ _) frac {2 \ pi} {T_ {1}} \ cdot t)} {x (t) = R_ {2} \ cdot cos (\ frac {2 \ pi} {T_ {2}} \ _ cdot t t, y) (t) = R_ {2} \ cdot sin (\ frac {2 \ pi} {T_ {2}} \ cdot t)}, (5)$$

(5) का उपयोग करते हुए, हम चंद्रमा की कक्षा के लिए निर्देशांक की एक जोड़ी प्राप्त करते हैं:

$$

$$\ binom {X_ {g} (t) = X (t) + x (t)} {Y_ {g} (t) = Y (t) + y (t)}, (6)$$

हमने उन बिंदुओं की संख्या निर्धारित की है जिन पर निर्देशांक N = 1000 और पृथ्वी के घूर्णन काल के अंतराल पर असतत समय की गणना की जाती है $$$dt = \ frac {T_ {1}} {N}$ । हम एक कार्यक्रम लिखेंगे और सकारात्मक समन्वय परिवर्तन क्षेत्र के लिए एक ग्राफ बनाएंगे:


हमें मिलता है:


चित्र 1

बनाया गया शेड्यूल आपको प्रशिक्षण कार्य का विस्तार करने और यह देखने की अनुमति देता है कि यदि चंद्रमा की कक्षा का त्रिज्या है तो चंद्रमा की कक्षा क्या होगी $$$R_ {2} = 3.844 \ cdot 10 ^ {7}$ । । पाठक को यह स्पष्ट है कि खगोल विज्ञान में विशेष ज्ञान भी नहीं है कि चंद्रमा पृथ्वी के गैर-गुरुत्वाकर्षण क्षेत्रों में ऐसी कक्षा नहीं हो सकता है, और एक काल्पनिक त्रिज्या का उपयोग लूप की उपस्थिति के लिए स्थितियों का अध्ययन करने के लिए किया जाता है । हम कार्यक्रम में उचित बदलाव करेंगे:


हमें मिलता है:


Fig.2

अंजीर में दिखाए गए चंद्रमा की कक्षाओं की तुलना करना। 1 और 2, हम उनके महत्वपूर्ण अंतर पाते हैं। इन अंतरों के कारणों की व्याख्या करने के लिए, पहले और दूसरे मामलों में चंद्रमा के रैखिक वेग और पृथ्वी के रैखिक वेग की तुलना करना आवश्यक है।

चूंकि सूर्य के सापेक्ष पृथ्वी के रैखिक वेग की दिशा, साथ ही पृथ्वी के सापेक्ष चंद्रमा के रैखिक वेग की दिशा, समय में परिवर्तन, और वेग परिमाण में स्थिर रहता है।

एक सहायक प्रणाली में चंद्रमा और पृथ्वी के रैखिक वेग के अनुपात की मात्रात्मक विशेषता के रूप में, किसी को पृथ्वी के रैखिक वेग मॉड्यूल और पृथ्वी के रैखिक वेग की दिशा पर चंद्रमा के रैखिक वेग के प्रक्षेपण के बीच अंतर चुनना चाहिए:

$$

$$v_ {o} (t) = \ left | \ vec {V} (t) \ right | - \ frac {(\ vec {V} (t) \ cdot \ vec {v} (t))} {\ left | \ vec {V} (t) \ right |}, (7)$$

हम उन कार्यों को परिभाषित करते हैं जो पृथ्वी और चंद्रमा की गति के घटकों के परिवर्तन के नियमों का वर्णन करते हैं:

$$

$$\ _ {मैट्रिक्स} V_ {x} (t) = \ frac {d} {dt} X (t), V_ {y} (t) = \ frac {d} {dt} Y (t) & \\ vx (t) = \ frac {d} {dt} x (t), vy (t) = \ frac {d} {dt} y (t) \ end {मैट्रिक्स}, (8)$$

प्रक्षेपण को ध्यान में रखते हुए, परिणामस्वरूप गति निर्धारित करने के लिए, हम संबंध का उपयोग करते हैं:

$$$D (t) = \ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} - \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}} \ cdot \ frac {V_ {x} (t) \ cdot vx (t) + V_ {y} (t) \ cdot vy (t)} {\ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} \ cdot \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}}}, (9)$

हम एक कार्यक्रम को ध्यान में रखते हुए (5), (8), (9) और चंद्रमा की कक्षा की त्रिज्या लिखेंगे $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ किमी।:


हमें मिलता है:


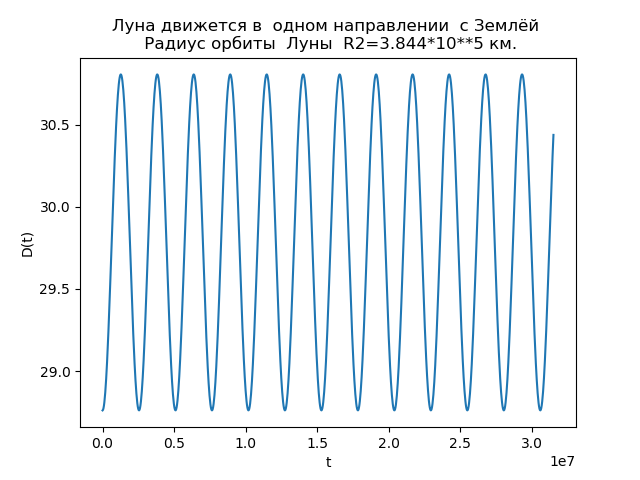चित्र 3।

हम एक कार्यक्रम को ध्यान में रखते हुए (5), (8), (9) और चंद्रमा की कक्षा आर 2 = 3.844 * 10 ** 7 किमी: लिखेंगे।


हमें मिलता है:


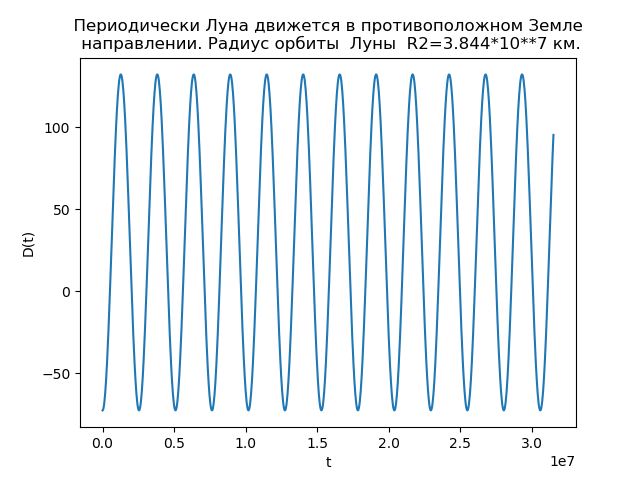चित्र 4।

आश्रितों का विश्लेषण हमें कक्षाओं में अंतर के कारण की व्याख्या करने की अनुमति देता है। समारोह डी (टी) के लिए $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ किमी हमेशा धनात्मक होता है, अर्थात चंद्रमा हमेशा पृथ्वी की गति की दिशा में चलता है और कोई छोर नहीं बनता है। पर $$$R_ {2} = 3.844 \ cdot 10 ^ {7}$ किमी मूल्य $$$डी (टी)$ नकारात्मक मान लेता है, और ऐसे समय होते हैं जब चंद्रमा पृथ्वी की गति की दिशा के विपरीत दिशा में चलता है, और इसलिए कक्षा में छोर होते हैं। यह गणना में चंद्रमा की गैर-मौजूद कक्षा का उपयोग करने का अर्थ था।

पृथ्वी से जुड़े संदर्भ के फ्रेम में मंगल की कक्षा का निर्माण

।


हेलियोसेंट्रिक रेफरेंस सिस्टम (सिस्टम K) में, पृथ्वी त्रिज्या के एक चक्र में चलती है $$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ किमी, परिसंचरण अवधि $$$T_ {1} = $ 365.2$ दिन, मंगल एक दीर्घवृत्त के साथ चलता है, जिसकी अर्ध-प्रमुख धुरी है $$$am = 2.28 \ cdot 10 ^ {8}$ किमी, मंगल ग्रह की क्रांति की अवधि $$$T_ {m} = $ 689.9$ दिन।, कक्षा की विलक्षणता $$$ई = $ 0.09$ [3]। पृथ्वी की गति का वर्णन रेडियस वेक्टर R (t) द्वारा किया गया है जिसे अभिव्यक्ति (3) द्वारा परिभाषित किया गया है। इस तथ्य के कारण कि मंगल की कक्षा एक दीर्घवृत्त, निर्भरता है $$$x = x (t), y = y (t)$ समय-समय पर पैरामीट्रिक रूप से सेट होते हैं [4]:

$$$x (\ varepsilon) = a_ {m} \ cdot (cos (\ varepsilon) -e$ (10)

$$$y (\ varepsilon) = a_ {m} \ cdot \ sqrt {1-e ^ {2}} \ cdot पाप (\ varepsilon)$ , (11)

$$$t (\ varepsilon) = \ frac {T_ {m}} {2 \ pi} \ cdot (\ varepsilon-e \ cdot sin (\ varepsilon))$ , (12)

एक पूर्ण दीर्घवृत्त क्रांति पैरामीटर <img में परिवर्तन से मेल खाती है $$$\ _ varepsilon$ 0 से $$$2 \ pi$ । मंगल की कक्षा का निर्माण करने के लिए, एक ही समय में त्रिज्या वैक्टर के निर्देशांक की गणना करना आवश्यक है, जो हेलियोसेंट्रिक संदर्भ फ्रेम में पृथ्वी और मंगल की स्थिति का वर्णन करता है, फिर संबंध के अनुसार $$$\ vec {r ^ {'}} (t) = \ vec {r} (t) - \ vec {R} (t)$ पृथ्वी से जुड़े संदर्भ के फ्रेम में मंगल के निर्देशांक की गणना करें।

पृथ्वी से जुड़े संदर्भ फ्रेम में मंगल की कक्षा का निर्माण करने के लिए, हम पृथ्वी और मंगल की कक्षाओं के पहले दिए गए मापदंडों का उपयोग करते हैं, संबंधों (10) - (12), और पृथ्वी के निर्देशांक के लिए भी संबंध:

$$$X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} t)$ , (13)

$$$Y (t) = R_ {1} \ cdot पाप (\ frac {2 \ pi} {T_ {1}} t)$ , (14)

यह ध्यान दिया जाना चाहिए कि सूर्य के चारों ओर मंगल की क्रांति की अवधि है $$$K = 9$ , फिर उन बिंदुओं की संख्या जिस पर गणना की जानी चाहिए और संबंधों के बीच की दूरी निर्धारित की जाएगी:

$$$N = 4000 \ cdot K, \ varepsilon_ {i} = \ frac {2 \ pi} {N} \ cdot i, i = 0 ... N$ (15)


हमें मिलता है:


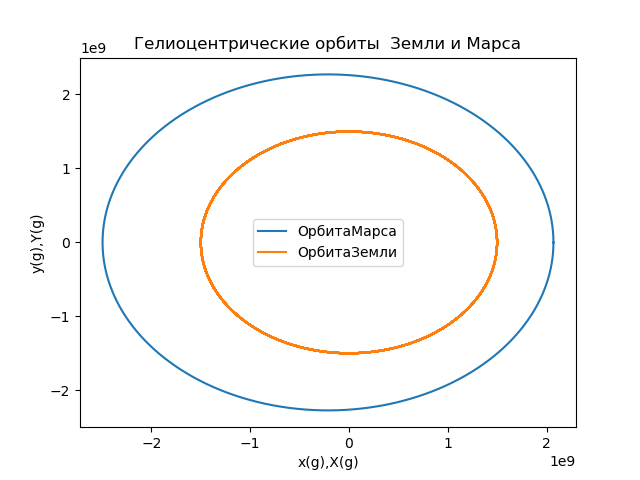चित्रा 5

हम पृथ्वी से जुड़े संदर्भ फ्रेम में मंगल की स्थिति का वर्णन करने वाले त्रिज्या वेक्टर के निर्देशांक की गणना करते हैं, और संबंध का उपयोग करके कक्षाओं (छवि 6) का निर्माण करते हैं:

$$$X1_ {i} = x (\ varepsilon_ {i}) - X (t (\ varepsilon_ {i})), y1_ {i} = y (\ varepsilon_ {i) - Y (t (varepsilon_ {i)) ))$ (16)


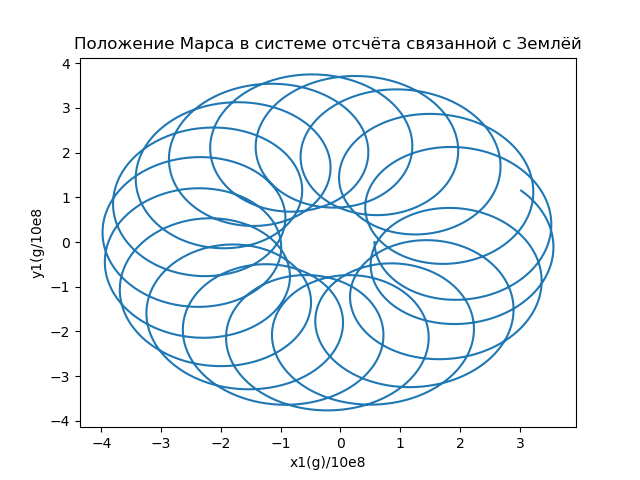चित्रा 6

मंगल की गति की एक अन्य महत्वपूर्ण विशेषता (मुख्य रूप से अंतरग्रहीय अंतरिक्ष उड़ानों के लिए) पृथ्वी और मंगल ग्रह के बीच की दूरी है, जो त्रिज्या सदिश के मापांक से निर्धारित होती है, जो पृथ्वी से जुड़े संदर्भ के फ्रेम में मंगल की स्थिति का वर्णन करता है। स्थलीय वर्षों में मापी गई पृथ्वी और मंगल के बीच की दूरी की निर्भरता चित्र 7 में प्रस्तुत की गई है।


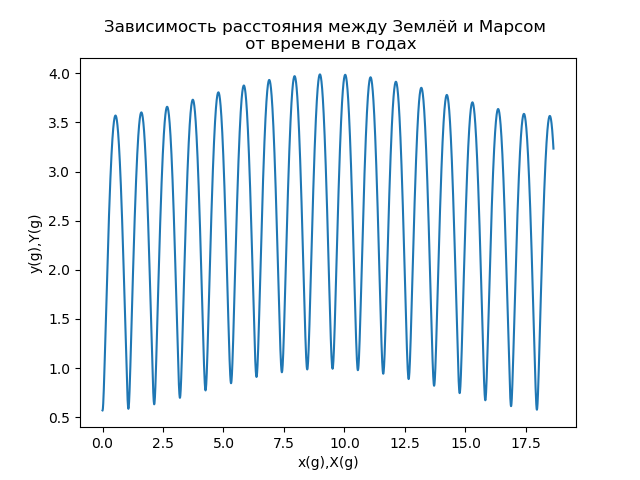चित्र 7

अंजीर। 7 में दिखाई गई निर्भरता का विश्लेषण दर्शाता है कि पृथ्वी और मंगल के बीच की दूरी समय की एक जटिल आवधिक क्रिया है। यदि हम सिग्नल सिद्धांत [5] की शब्दावली का उपयोग करते हैं, तो हम निर्भरता एस (टी) के बारे में कह सकते हैं कि यह एक आयाम-संग्राहक संकेत है, जिसे आमतौर पर उच्च-आवृत्ति (वाहक) और निम्न-आवृत्ति फ़ंक्शन के दो कार्यों के उत्पाद के रूप में दर्शाया जाता है जो आयाम मॉड्यूलेशन (लिफाफा) को परिभाषित करता है। :

$$$u (t) = (\ bar {u} + a + cdot sin (\ omega_ {1} t)) \ cdot (1+ \ Delta a \ cdot sin (\ omega_ {2} t))$ (17)

जहाँ $$$\ bar {u}$ - फ़ंक्शन का निरंतर घटक $$$यू (टी)$ ; $$$एक$ - संकेत आयाम; $$$\ omega_ {1}$ - वाहक आवृत्ति; $$$\ Delta एक$ - फ़ंक्शन का आयाम जो आयाम मॉडुलन की गहराई सेट करता है; $$$\ _ omega_ {2}$ - modulating फ़ंक्शन की आवृत्ति।

अंजीर 7 से यह देखा जा सकता है कि वाहक की अवधि लगभग 2 वर्ष है, मॉड्यूलेटिंग फ़ंक्शन की अवधि लगभग 17 वर्ष है: 6]।

हैली के धूमकेतु के हेलियोसेंट्रिक कक्षा का निर्माण

आखिरी बार हैली का धूमकेतु 9 फरवरी, 1986 को अपने पेरिहेलियन (सूर्य के निकटतम कक्षा बिंदु) से गुजरा। (सूर्य को मूल में स्थित माना जाता है।)

उस समय हैली के धूमकेतु के निर्देशांक और वेग घटक बराबर थे $$$p_ {0} = (0.325514, 0.459460, 0.166229)$ और $$$v_ {0} = (-9.096111, –6.916686, –1.305721)$ क्रमशः, और यहाँ की दूरी लंबाई की खगोलीय इकाइयों में व्यक्त की जाती है - a.u.d., या बस a.u. (खगोलीय इकाई, यानी, पृथ्वी की कक्षा के प्रमुख प्रमुख अर्धचालक की लंबाई), और वर्षों में समय। माप की इन इकाइयों में, धूमकेतु की गति के तीन आयामी समीकरणों का रूप है:

$$

$$\ बाईं \ {\ शुरू {मैट्रिक्स} \ frac {d ^ {2} x} {dt ^ {2}} = - \ frac {\ mu \ cdot x} {r ^ {3}} \\ \ frac { d ^ {2} y} {dt ^ {2}} = - \ frac {\ _ mu \ cdot y} {r ^ {3}} \\ \ frac {d ^ {2} z} {dt ^ {2} } = - \ frac {\ _ mu \ cdot z} {r ^ {3}} \ end {मैट्रिक्स} \ right। (18)$$

(18)

जहां: $$$\ mu = 4 \ pi ^ {2}, r = \ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}$


हमें मिलता है:









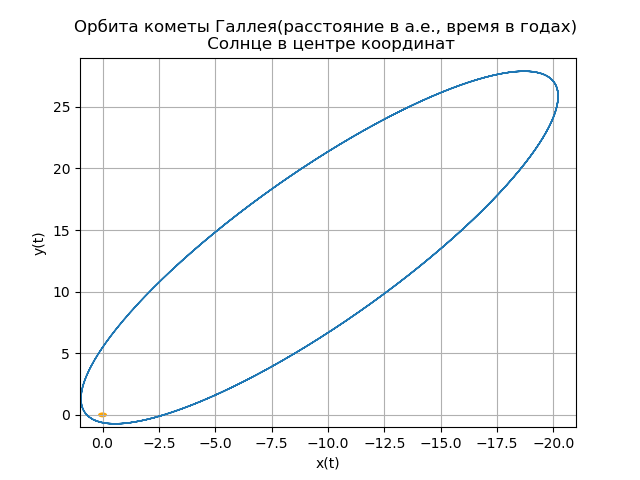
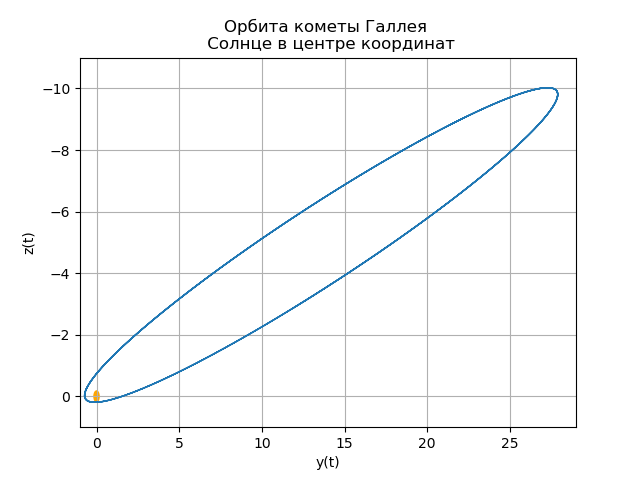
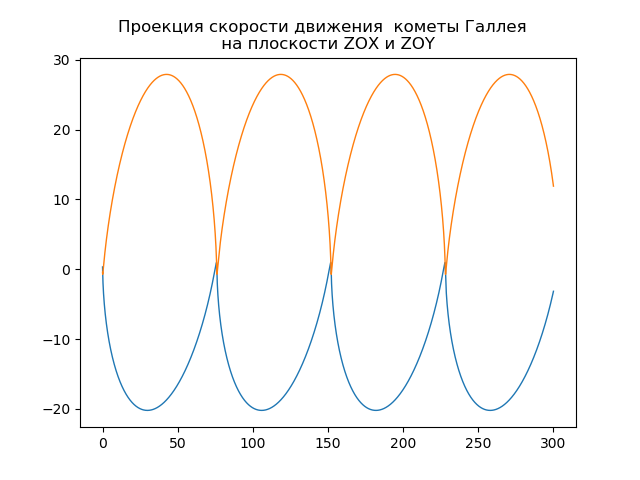आपका अपना धूमकेतु

एक प्रयोग करके देखें। रात में, आप अपने टेलीस्कोप को अपने घर से दूर पहाड़ी की चोटी पर माउंट करते हैं। रात स्पष्ट, बादल रहित, तारों से भरी होनी चाहिए और, अगर भाग्य आप पर मुस्कुराए: सुबह ०.३० बजे आप एक नए धूमकेतु को देखेंगे।

निम्नलिखित रातों पर बार-बार टिप्पणियों के बाद, आप उस पहली रात को इसके निर्देशांक की गणना करने में सक्षम होंगे। हेलियोसेंट्रिक कोऑर्डिनेट सिस्टम में निर्देशांक: P0 = (x0, y0, z0) और वेग वेक्टर v0 = (vx0, vy0, vz0)।

इस डेटा का उपयोग करके, निर्धारित करें:

• पेरिहेलियन पर सूर्य से धूमकेतु की दूरी (सूर्य के निकटतम कक्षा का बिंदु) और उदासीनता पर (सूर्य से सबसे दूर कक्षा का बिंदु);
• पेरिहेलियन से गुजरते समय और अपहेल के माध्यम से धूमकेतु की गति;
• सूर्य के चारों ओर धूमकेतु की क्रांति की अवधि;
• अगली दो तिथियां धूमकेतु पेरिहेलियन से गुजरती हैं।

यदि हम खगोलीय इकाइयों में दूरी और वर्षों में समय को मापते हैं, तो धूमकेतु की गति का समीकरण रूप लेगा (18)। अपने स्वयं के धूमकेतु के लिए, हैली के धूमकेतु के रूप में एक ही क्रम के प्रारंभिक निर्देशांक और गति का चयन करें।

यदि आवश्यक हो, तो प्रारंभिक स्थिति और वेग वेक्टर का एक मनमाना विकल्प फिर से बनाएं जब तक कि आपको एक ऐसी विलक्षण सनकी कक्षा न मिल जाए जो पृथ्वी की कक्षा (जैसे अधिकांश वास्तविक धूमकेतु) से आगे जाती है।

संदर्भ:

1. फिजमैन आर।, फिजिक्स में लेट्सन आर।, सैंड्स एम। फेनमैन लेक्चर्स। तीसरा संस्करण। टी। 1.-2। एम .: मीर, 1977।
2. मतवेव ए.एन. मैकेनिक्स एंड थ्योरी ऑफ़ रिलेटिविटी। एम।: उच्चतर। स्कूल।, 1986।
3. भौतिक विश्वकोश। टी। 3. एम .: बिग रूसी एनसाइक्लोपीडिया, 1992।
4. लन्दौ एल। डी।, सैद्धांतिक भौतिकी में ई.एम. कोर्स। यांत्रिकी। एम .: फू-मेटगिज़, 1958।
5. बसाकोव एस.आई. रेडियो इंजीनियरिंग सर्किट और सिग्नल। एम।: उच्चतर। स्कूल।, 1988।
6. पोर्शनेव सी.वी. मैथेकैड पैकेज का उपयोग करके भौतिक प्रक्रियाओं का कंप्यूटर सिमुलेशन।