हम 1C पर कैसे हैं: एंटरप्राइज़ बीजीय समीकरणों के सिस्टम को हल करता है

विशेष रूप से रैखिक बीजगणितीय समीकरणों की सामान्य और हल करने वाली प्रणालियों में संख्यात्मक मैट्रिक्स के साथ काम करना एक क्लासिक गणितीय और एल्गोरिथम समस्या है जो व्यापक रूप से मॉडलिंग और व्यावसायिक प्रक्रियाओं के एक विशाल वर्ग की गणना करने में उपयोग किया जाता है (उदाहरण के लिए, जब लागत की गणना)। 1 सी का निर्माण और संचालन करते समय: एंटरप्राइज़ कॉन्फ़िगरेशन, कई डेवलपर्स को मैन्युअल रूप से SLAU गणना एल्गोरिदम को लागू करने की आवश्यकता के साथ सामना करना पड़ा, और फिर एक समाधान के लिए लंबे इंतजार की समस्या के साथ।

"ए.सी.: एंटरप्राइज" 8.3.14 में कार्यक्षमता शामिल होगी जो ग्राफ सिद्धांत पर आधारित एल्गोरिथ्म का उपयोग करके रैखिक समीकरणों की प्रणालियों को हल करने में लगने वाले समय को काफी कम कर सकती है।

यह एक विरल संरचना वाले डेटा पर उपयोग के लिए अनुकूलित है (जो कि समीकरणों में 10% से अधिक नॉनजेरो गुणांक वाले हैं) और, औसतन और सर्वोत्तम मामलों में, एसिमप्टोटिक्स Θ (nlog) (n) log (n)) को प्रदर्शित करता है, जहां n है चर की संख्या, और सबसे खराब स्थिति में (जब सिस्टम पूर्ण ~ 100% है), इसका विषम व्यवहार शास्त्रीय एल्गोरिदम (Θ (एन ³ )) के साथ तुलनीय है। इसके अलावा, सिस्टम पर ~ 10 ⁵ अज्ञात के साथ, एल्गोरिथ्म विशिष्ट रैखिक बीजगणित पुस्तकालयों (उदाहरण के लिए, सुपरलू या लैपैक ) में लागू किए गए लोगों की तुलना में सैकड़ों बार त्वरण दिखाता है।


महत्वपूर्ण: लेख और वर्णित एल्गोरिथ्म में विश्वविद्यालय के पहले वर्ष के स्तर पर रैखिक बीजगणित और ग्राफ सिद्धांत की समझ की आवश्यकता होती है।

ग्राफ के रूप में SLAE की प्रस्तुति

रैखिक समीकरणों की सरलतम विरल प्रणाली पर विचार करें:


ध्यान दें: सिस्टम बेतरतीब ढंग से उत्पन्न होता है और बाद में एल्गोरिदम के चरणों को प्रदर्शित करने के लिए उपयोग किया जाएगा

इस पर पहली नज़र में, एक अन्य गणितीय वस्तु के साथ एक संघ उत्पन्न होता है - ग्राफ आसन्न मैट्रिक्स। तो क्यों न डेटा को आसन्न सूचियों में परिवर्तित किया जाए, रनटाइम पर रैम को बचाया जाए और गैर-शून्य गुणांकों तक पहुंच को तेज किया जाए?

ऐसा करने के लिए, यह मैट्रिक्स को स्थानांतरित करने और अक्रियाशील "A [i] [j] = z i को स्थापित करने के लिए i-th चर गुणांक z के साथ j-th समीकरण में प्रवेश करता है" , और फिर किसी भी गैर-शून्य [i] [j] के लिए संबंधित बढ़त का निर्माण करता है। वर्टेक्स से मैं वर्टेक्स जे।

परिणामी ग्राफ इस तरह दिखेगा:



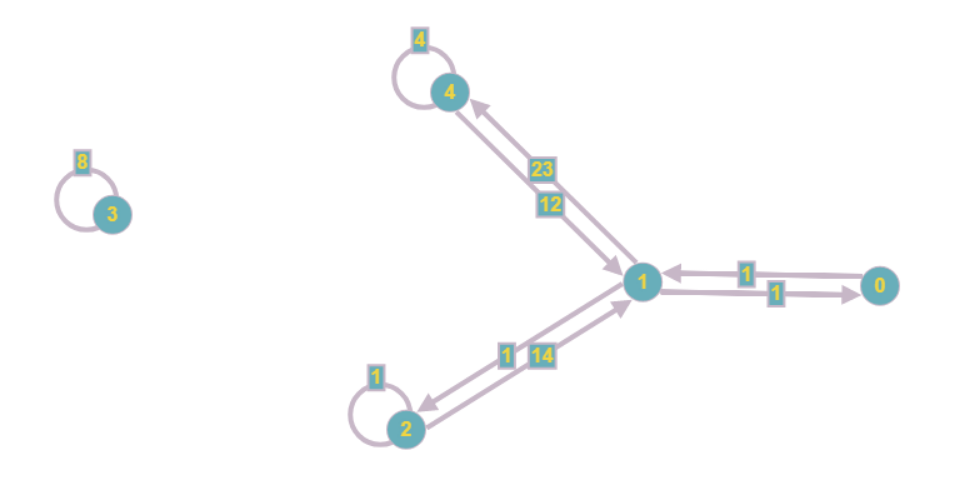
यहां तक ​​कि नेत्रहीन, यह कम बोझिल हो जाता है, और स्पर्शोन्मुख स्मृति लागत ओ (एन ² ) से घटकर ओ (एन + एम) हो जाती है, जहां एम सिस्टम में गुणांक की संख्या है।

कमजोर रूप से जुड़े घटकों का अलगाव

दूसरा एल्गोरिथम विचार जो परिणामी इकाई पर विचार करते समय ध्यान में आता है: "फूट डालो और जीतो" के सिद्धांत का उपयोग। ग्राफ़ के संदर्भ में, यह कोने के सेट को कमजोर रूप से जुड़े घटकों में अलग करने की ओर जाता है।

मैं आपको याद दिलाता हूं कि कमजोर रूप से जुड़ा घटक वर्टिस का ऐसा सबसेट है, जो अधिकतम शामिल है कि किसी भी दो के बीच एक अप्रत्यक्ष ग्राफ में किनारों से एक पथ मौजूद है। हम मूल एक से अप्रत्यक्ष ग्राफ प्राप्त कर सकते हैं, उदाहरण के लिए, प्रत्येक किनारे के विपरीत जोड़कर (बाद में हटाने के साथ)। फिर कनेक्शन के एक शीर्ष में वे सभी कोने शामिल होंगे जो हम उस समय तक पहुंच सकते हैं जब हम ग्राफ में गहराई से घूमते हैं।

कमजोर रूप से जुड़े घटकों के अलग होने के बाद, ग्राफ निम्नलिखित रूप लेगा:



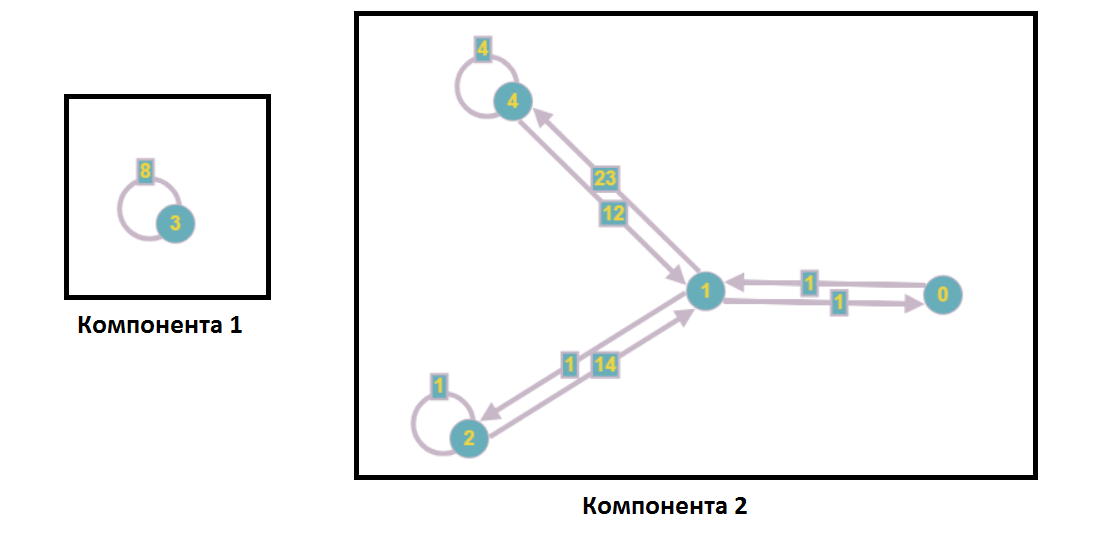
रैखिक समीकरणों की एक प्रणाली के विश्लेषण के भाग के रूप में, इसका मतलब है कि पहले घटक से एक भी शीर्ष शीर्ष दूसरे घटक की संख्या के साथ समीकरणों में शामिल नहीं है और इसके विपरीत, अर्थात्, हम इन उपतंत्रों को स्वतंत्र रूप से (उदाहरण के लिए समानांतर में) हल कर सकते हैं।

ग्राफ वर्टेक्स में कमी

एल्गोरिथ्म का अगला चरण ठीक वैसा ही है जैसा कि विरल मैट्रिस के साथ काम करने के लिए अनुकूलन है। उदाहरण से ग्राफ़ में भी "लटकी हुई" चोटियाँ हैं, जिसका अर्थ है कि कुछ समीकरणों में केवल एक अज्ञात शामिल है और, जैसा कि हम जानते हैं, इस अज्ञात का मान खोजना आसान है।

इस तरह के समीकरणों को निर्धारित करने के लिए, इस सरणी तत्व की संख्या वाले समीकरण में शामिल चर की संख्या वाली सूचियों को संग्रहीत करना प्रस्तावित है। फिर, जब सूची इकाई के आकार तक पहुंच जाती है, तो हम बहुत ही "केवल" वर्टेक्स को कम कर सकते हैं, और बाकी समीकरणों को अन्य समीकरणों में सूचित कर सकते हैं जिसमें यह वर्टेक्स प्रवेश करता है।

इस प्रकार, हम घटक को पूरी तरह से संसाधित करने के तुरंत बाद उदाहरण से वर्टेक्स 3 को कम कर सकते हैं:

$$

$$8 $_3 =$$

हम समीकरण 0 के साथ इसी तरह आगे बढ़ते हैं, क्योंकि इसमें केवल एक चर होता है:

$$

$$1 $x_1 = 1 Inc.x_1 = 1$$

इस परिणाम को खोजने के बाद अन्य समीकरण भी बदल जाएंगे:

$$$ $ प्रदर्शन $ $ 1⋅_1 ​​+ 1 display_2 = 3 3.1_2_2 = 3-1 = 2 $ $ प्रदर्शन $ $

ग्राफ निम्नलिखित रूप लेता है:



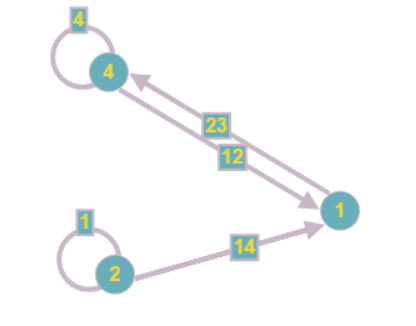
ध्यान दें कि एक शीर्ष को कम करते समय, अन्य भी दिखाई दे सकते हैं जिसमें एक अज्ञात भी होता है। इसलिए एल्गोरिथ्म के इस चरण को दोहराया जाना चाहिए जब तक कि कम से कम एक कोने को कम नहीं किया जा सकता है।

ग्राफ़ का पुनर्निर्माण

सबसे चौकस पाठक यह नोटिस कर सकते हैं कि एक स्थिति संभव है जिसमें ग्राफ के प्रत्येक कोने में कम से कम दो होने की डिग्री होगी और निरंतरता को कम करने के लिए जारी रखना असंभव होगा।

इस तरह के ग्राफ का सबसे सरल उदाहरण: प्रत्येक वर्टेक्स में दो के बराबर घटना होती है, किसी भी कोने को कम नहीं किया जा सकता है।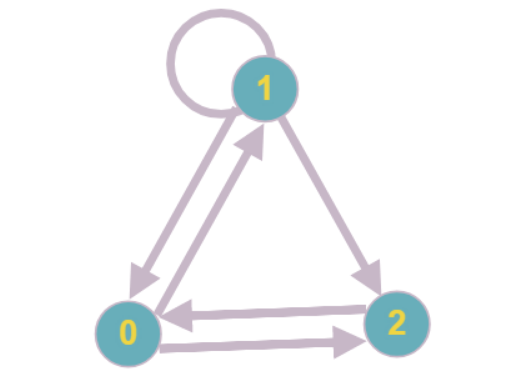



विरल मैट्रिस के लिए अनुकूलन के हिस्से के रूप में, यह माना जाता है कि इस तरह के सबग्राफ आकार में छोटे होंगे, हालांकि, आपको अभी भी उनके साथ काम करना होगा। अज्ञात के मूल्यों की गणना करने के लिए जो समीकरणों के सबसिस्टम का हिस्सा हैं, SLAEs को हल करने के लिए शास्त्रीय तरीकों का उपयोग करने का प्रस्ताव है (यही कारण है कि परिचय एक मैट्रिक्स के लिए जिसमें समीकरणों में सभी या लगभग सभी गुणांक नॉनजेरो हैं, हमारे एल्गोरिथ्म में समान असममित जटिलता होगी जैसे मानक वाले होते हैं। )।

उदाहरण के लिए, आप मैट्रिक्स फॉर्म में वापस आने के बाद शेष के सेट को ला सकते हैं और SLAE को हल करने के लिए गॉस विधि को लागू कर सकते हैं । इस प्रकार, हमें सटीक समाधान मिलेगा, और एल्गोरिथ्म की गति पूरी प्रणाली को संसाधित करने के कारण कम हो जाएगी, लेकिन इसका केवल कुछ हिस्सा।

एल्गोरिथम परीक्षण

एल्गोरिथ्म के सॉफ़्टवेयर कार्यान्वयन का परीक्षण करने के लिए, हमने बड़ी मात्रा के समीकरणों के कई वास्तविक सिस्टम, साथ ही बड़ी संख्या में यादृच्छिक रूप से उत्पन्न सिस्टम को लिया।
समीकरणों की एक यादृच्छिक प्रणाली की पीढ़ी दो यादृच्छिक कोने के बीच मनमाने वजन के किनारों के क्रमिक जोड़ के माध्यम से चली गई। कुल मिलाकर, सिस्टम 5-10% भरा हुआ था। समीकरणों की मूल प्रणाली में प्राप्त उत्तरों को प्रतिस्थापित करके समाधानों की शुद्धता को सत्यापित किया गया था।


सिस्टम 1,000 से 200,000 अज्ञात तक थे

प्रदर्शन की तुलना करने के लिए, हमने रैखिक बीजगणित की समस्याओं को सुलझाने के लिए सबसे लोकप्रिय पुस्तकालयों का उपयोग किया, जैसे कि सुपरलू और लैपैक। बेशक, ये पुस्तकालय समस्याओं की एक विस्तृत श्रेणी को हल करने पर केंद्रित हैं और इनमें SLAE का समाधान किसी भी तरह से अनुकूलित नहीं है, इसलिए गति में अंतर महत्वपूर्ण हो गया है।


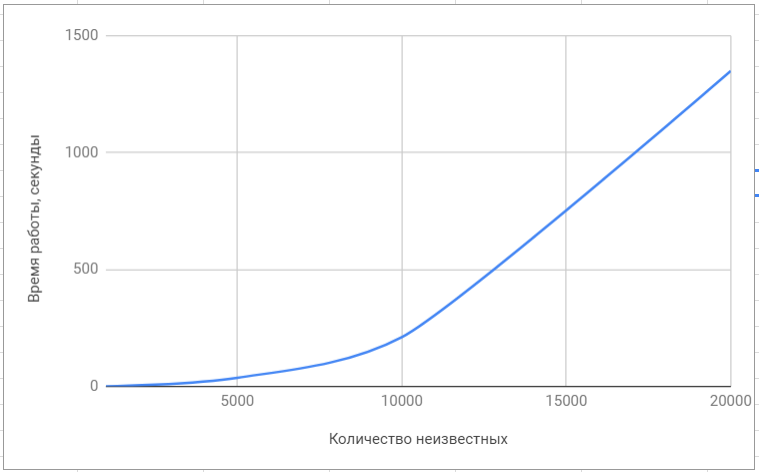लैपैक लाइब्रेरी का परीक्षण


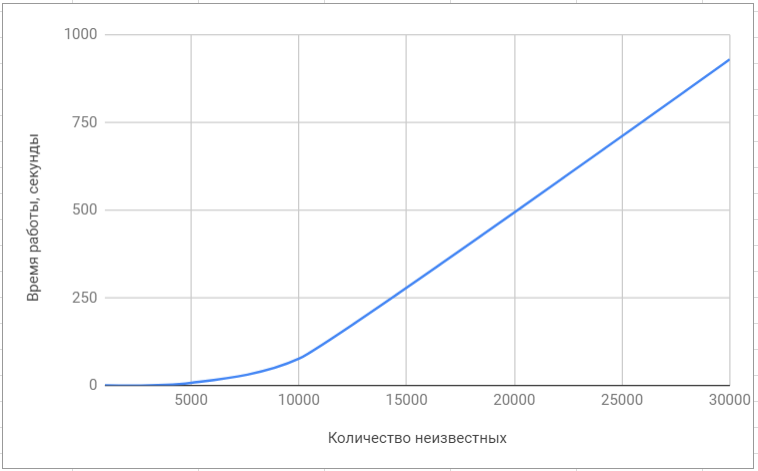पुस्तकालय 'सुपरलू' का परीक्षण

यहाँ लोकप्रिय एल्गोरिदम में लागू एल्गोरिदम के साथ हमारे एल्गोरिथ्म की अंतिम तुलना है:

निष्कर्ष

यहां तक ​​कि अगर आप 1 सी नहीं हैं: एंटरप्राइज़ कॉन्फ़िगरेशन डेवलपर, इस आलेख में वर्णित विचारों और अनुकूलन के तरीकों का उपयोग आप न केवल SLAEs को हल करने के लिए एक एल्गोरिथ्म को लागू करते समय कर सकते हैं, बल्कि मैट्रिसेस से जुड़ी रैखिक बीजगणित समस्याओं के एक पूरे वर्ग के लिए भी कर सकते हैं।

1C डेवलपर्स के लिए, हम कहते हैं कि SLAE समाधान की नई कार्यक्षमता कंप्यूटिंग संसाधनों के समानांतर उपयोग का समर्थन करती है, और आप उपयोग किए गए गणना थ्रेड्स की संख्या को समायोजित कर सकते हैं।