🚸 🏠 🏤 निश्चित इंटीग्रल्स की गणना: बुनियादी एल्गोरिदम 😉 👎 🌒

यह प्रकाशन एक खंड पर एक चर के कार्यों के अभिन्न की गणना के लिए सबसे सरल तरीकों का वर्णन करता है, जिसे चतुर्भुज सूत्र भी कहा जाता है। आमतौर पर, इन विधियों को मानक गणितीय पुस्तकालयों में लागू किया जाता है जैसे कि GNU साइंटिफिक लाइब्रेरी फॉर C, SciPy for Python, और अन्य। प्रकाशन का उद्देश्य यह प्रदर्शित करना है कि ये तरीके "हूड के तहत" कैसे काम करते हैं, और सटीकता और एल्गोरिदम के प्रदर्शन के कुछ मुद्दों पर ध्यान आकर्षित करते हैं। मैं द्विघात सूत्र और साधारण अंतर समीकरणों के संख्यात्मक एकीकरण के तरीकों के संबंध पर भी ध्यान देना चाहूंगा, जिसके बारे में मैं एक और प्रकाशन लिखना चाहता हूं।

अभिन्न की परिभाषा

एक समारोह के इंटीग्रल (रीमैन के अनुसार) $च (x)$ खंड पर $[ए; बी]$ निम्नलिखित सीमा को कहा जाता है:

१

$\ int_a ^ bf (x) dx = \ lim _ {\ Delta x \ to 0} \ sum_ {i = 0} ^ {n-1} f (\ xi_i) (x_ {i + 1} - x_i), ~ ~ (१)$

जहाँ $\ Delta x = \ max \ lbrace x_ {i + 1} - x_i \ rbrace$ - विभाजन की सुंदरता, $x_0 = एक$ । $x_n = b$ । $\ xi_i$ - खंड पर एक मनमाना संख्या $[x_i; x_ {i + 1}]$ ।

यदि फ़ंक्शन का अभिन्न अस्तित्व है, तो सीमा मूल्य विभाजन की परवाह किए बिना समान है, यदि केवल यह पर्याप्त रूप से छोटा होगा।

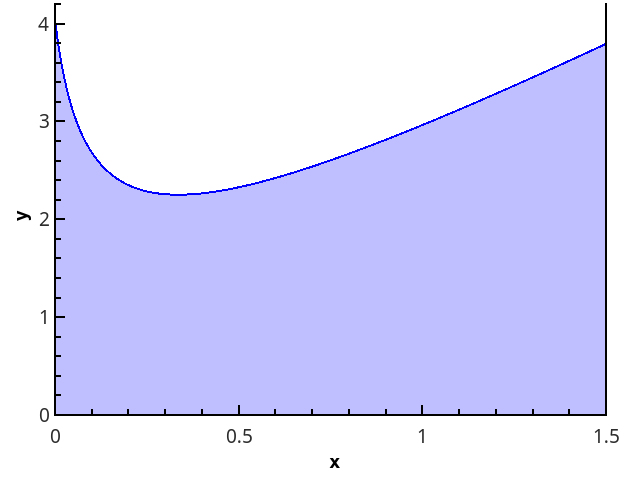
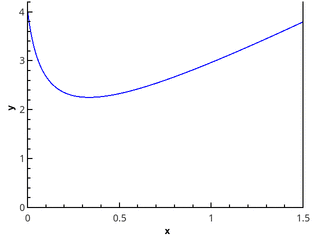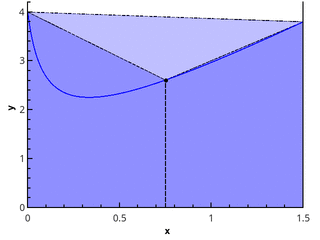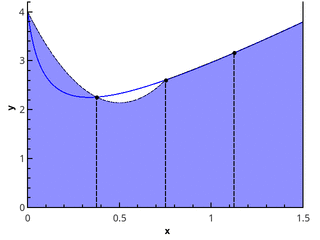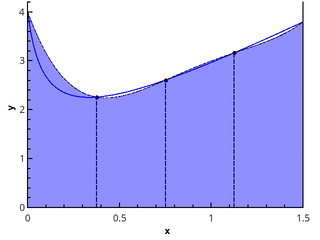
ज्यामितीय परिभाषा अधिक स्पष्ट है - अभिन्न 0 x अक्ष, फ़ंक्शन के ग्राफ, और सीधी रेखाओं x = a और x = b (आकृति में भरा हुआ क्षेत्र) से घिरा घुमावदार ट्रेपोज़ॉइड के क्षेत्र के बराबर है।

चतुर्भुज सूत्र

इंटीग्रल (1) की परिभाषा को फिर से फॉर्म में लिखा जा सकता है

ल ग भ ग

$I = \ int_a ^ b f (x) dx \ लगभग I_n = (b - a) \ sum_ {i = 0} ^ {n-1} w_i f (\ xi_i), ~~ (2)$

जहाँ $w_i$ - भारांक गुणांक, जिसका योग 1 के बराबर होना चाहिए, और गुणांक स्वयं - बढ़ती संख्या के साथ शून्य हो जाते हैं $एन$ जिन बिंदुओं पर फ़ंक्शन की गणना की जाती है।

अभिव्यक्ति (2) सभी चतुर्भुज सूत्रों का आधार है (यानी, अभिन्न की अनुमानित गणना के लिए सूत्र)। अंक का चयन करना चुनौती है $\ lbrace \ xi_i \ rbrace$ और वजन $w_i$ ताकि दाईं ओर का योग आवश्यक इंटीग्रल को यथासंभव सटीक रूप से अनुमानित करे।

कम्प्यूटेशनल कार्य

समारोह सेट $च (x)$ जिसके लिए अंतराल में किसी भी बिंदु पर मूल्यों की गणना के लिए एक एल्गोरिथ्म है $[ए; बी]$ (मेरा मतलब है कि फ़्लोटिंग-पॉइंट नंबर द्वारा दर्शाए गए अंक - वहां कोई ड्यूरिचलेट फ़ंक्शन नहीं हैं!)।

अभिन्न के अनुमानित मूल्य को खोजने के लिए आवश्यक है $\ int_a ^ b f (x) dx$ ।
समाधान पायथन 3.6 में लागू किया जाएगा।

विधियों की जांच करने के लिए, अभिन्न का उपयोग करें $\ int_0 ^ {3/2} \ left [2x + \ frac {1} {\ sqrt {x + 1/16}} \ right] dx = 17/4$ ।

टुकड़े टुकड़े निरंतर सन्निकटन

आदर्श रूप से सरल चतुर्भुज सूत्र अभिव्यक्ति के अनुप्रयोग से उत्पन्न होते हैं (1) "माथे में"

$I_n = \ sum_ {i = 0} ^ {n-1} f (\ xi_i) (x_ {i + 1} - x_i)$

क्योंकि अंकों द्वारा एक खंड को विभाजित करने की विधि से $\ lbrace x_i \ rbrace$ और अंक चुनें $\ lbrace \ xi_i \ rbrace$ सीमा मूल्य निर्भर नहीं करता है, तो हम उन्हें चुनते हैं ताकि उन्हें आसानी से गणना की जा सके - उदाहरण के लिए, हम विभाजन को समान रूप से लेते हैं, और फ़ंक्शन की गणना के बिंदुओं के लिए हम विकल्पों पर विचार करते हैं: 1) $\ xi_i = x_i$ ; 2) $\ xi_i = x_ {i + 1}$ ; 3) $\ xi_i = (x_i + x_ {i + 1}) / 2$ ।

हमें बाएं आयताकार, दाएं आयताकार और आयताकार के तरीके क्रमशः एक मध्य बिंदु के साथ मिलते हैं।

कार्यान्वयन

def _rectangle_rule(func, a, b, nseg, frac): """  .""" dx = 1.0 * (b - a) / nseg sum = 0.0 xstart = a + frac * dx # 0 <= frac <= 1    , #    , #     dx for i in range(npoints): sum += func(xstart + i * dx) return sum * dx def left_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, nseg, 0.0) def right_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, npoints, 1.0) def midpoint_rectangle_rule(func, a, b, nseg): """    """ return _rectangle_rule(func, a, b, nseg, 0.5)

द्विघात सूत्रों के प्रदर्शन का विश्लेषण करने के लिए, हम निर्देशांक में त्रुटि का एक ग्राफ बनाते हैं "अंकों की संख्या संख्यात्मक परिणाम और सटीक एक के बीच का अंतर है।"

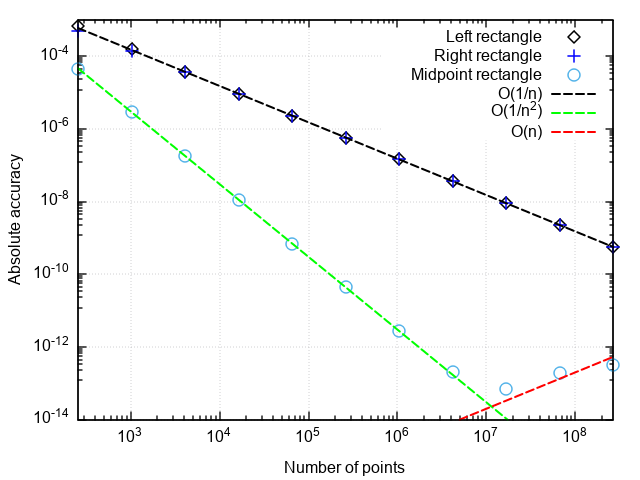
आप क्या नोटिस कर सकते हैं:

मध्य बिंदु के साथ एक सूत्र दाएं या बाएं डॉट की तुलना में बहुत अधिक सटीक है
मध्यबिंदु के साथ सूत्र की त्रुटि अन्य दो की तुलना में तेज़ी से गिरती है
बहुत छोटे विभाजन के साथ, मध्यबिंदु के साथ सूत्र की त्रुटि बढ़ने लगती है
पहले दो बिंदु इस तथ्य से संबंधित हैं कि मिडपॉइंट के साथ आयतों के सूत्र में एक दूसरा सन्निकटन क्रम है, अर्थात्। $| I_n - I | = O (1 / n ^ 2)$ , और दाएं और बाएं आयतों के सूत्र पहले क्रम हैं, अर्थात्। $| I_n - I | = O (1 / n)$ ।
एकीकरण चरण की पीसने के दौरान त्रुटि में वृद्धि गोलाई की अवधि में वृद्धि के साथ जुड़ी हुई है जब बड़ी संख्या में शब्द सम्‍मिलित होते हैं। यह त्रुटि जैसे बढ़ती है $| I_n - I | = O (1 / n)$ यह मशीन सटीकता को प्राप्त करने के लिए एकीकरण की अनुमति नहीं देता है।
निष्कर्ष: दाएं और बाएं बिंदुओं के साथ आयतों के तरीकों में कम सटीकता है, जो विभाजन के शोधन के साथ धीरे-धीरे बढ़ती है। इसलिए, वे केवल प्रदर्शन प्रयोजनों के लिए समझ में आता है। मिडपॉइंट के साथ आयतों की विधि में उच्च सन्निकटन क्रम होता है, जो इसे वास्तविक अनुप्रयोगों में उपयोग करने का मौका देता है (नीचे उस पर अधिक)।

टुकड़े-टुकड़े रैखिक सन्निकटन

अगला तार्किक कदम एक लीनियर फ़ंक्शन द्वारा सब-सेगमेंट पर पूर्णांक फ़ंक्शन को अनुमानित करना है, जो ट्रेपेज़ियम के द्विघात सूत्र देता है:

$I_n = \ sum_ {i = 0} ^ {n-1} \ frac {f (x_i) + f (x_ {i + 1})} {2} (x_ {i + 1} - x_i) ~~ ( 3)$

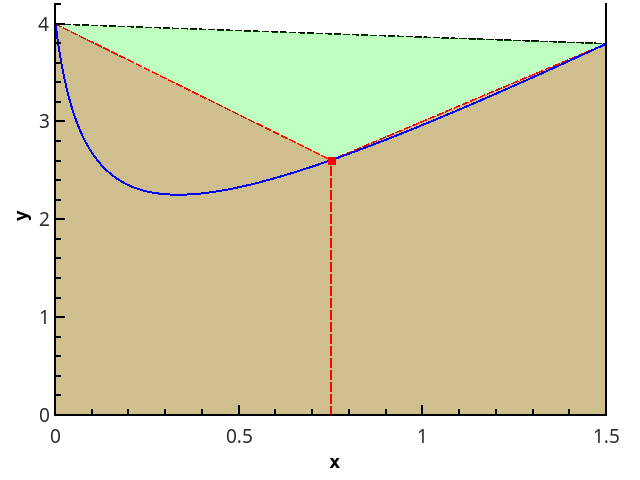
एन = 1 और एन = 2 के लिए ट्रैपोज़ाइडल विधि का चित्रण।

एक समान ग्रिड के मामले में, विभाजन के सभी खंडों की लंबाई बराबर होती है, और सूत्र का रूप होता है

$I_n = h \ left (\ frac {f (a) + f (b)} {2} + \ sum_ {i = 1} ^ {n-1} f (a + ih) \ right), ~ h = \ frac {बा} {n} ~~ (3a)$

कार्यान्वयन

 def trapezoid_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" dx = 1.0 * (b - a) / nseg sum = 0.5 * (func(a) + func(b)) for i in range(1, nseg): sum += func(a + i * dx) return sum * dx

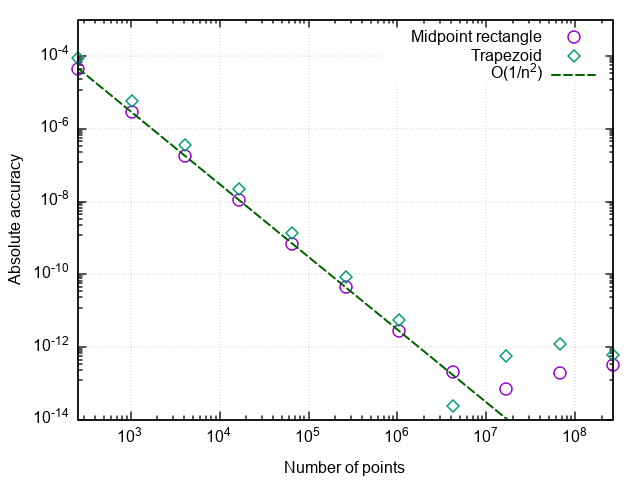
स्प्लिट पॉइंट्स की संख्या के आधार पर एरर को प्लॉट करने के बाद, हम देखते हैं कि ट्रेपोज़ॉइड विधि में एक दूसरा सन्निकटन क्रम भी है और आम तौर पर मिडपॉइंट आयत विधि (इसके बाद बस आयत विधि) से थोड़ा अलग परिणाम देता है।

गणना सटीकता नियंत्रण

इनपुट पैरामीटर के रूप में विभाजन बिंदुओं की संख्या निर्धारित करना बहुत व्यावहारिक नहीं है, क्योंकि आमतौर पर एक दिए गए विभाजन घनत्व के साथ अभिन्न की गणना करना आवश्यक नहीं है, लेकिन किसी दिए गए त्रुटि के साथ। यदि इंटीग्रैंड को पहले से जाना जाता है, तो हम पहले से त्रुटि का अनुमान लगा सकते हैं और एक एकीकरण कदम चुन सकते हैं ताकि निर्दिष्ट सटीकता निश्चित रूप से प्राप्त हो। लेकिन यह शायद ही कभी व्यवहार में है (और सामान्य तौर पर, क्या यह आसान नहीं है, पहले से ज्ञात फ़ंक्शन के साथ, पहले से इंटीग्रल को एकीकृत करने के लिए?) इसलिए, किसी दिए गए त्रुटि के लिए कदम को स्वचालित रूप से समायोजित करने के लिए एक प्रक्रिया आवश्यक है।

इसे कैसे लागू किया जाए? त्रुटि के आकलन के लिए सरल तरीकों में से एक - रन नियम - एन और 2 एन अंकों से गणना की गई इंटीग्रल के मूल्यों में अंतर, एक त्रुटि अनुमान देता है: $\ Delta_ {2n} \ लगभग | I_ {2n} - I_n |$ । एक केंद्रीय बिंदु के साथ आयतों की विधि की तुलना में एक विभाजन की सुंदरता को दोगुना करने के लिए ट्रेपेज़ॉइड विधि अधिक सुविधाजनक है। ट्रैपोज़ॉइड विधि द्वारा गणना करते समय, अंकों की संख्या को दोगुना करने के लिए, फ़ंक्शन के नए मूल्यों की आवश्यकता पिछले विभाजन के खंडों के बीच में ही होती है, अर्थात्। अभिन्न के पिछले सन्निकटन का उपयोग अगले गणना के लिए किया जा सकता है।

आयत विधि के लिए और क्या अच्छा है?

आयत विधि सेगमेंट के सिरों पर फ़ंक्शन के मूल्यों की गणना करने की आवश्यकता नहीं है। इसका मतलब यह है कि इसका उपयोग उन कार्यों के लिए किया जा सकता है जिनमें खंड के किनारों पर पूर्णांक विशेषताएं हैं (उदाहरण के लिए, पाप x / x या x ^-1/2 0 से 1 तक)। इसलिए, नीचे दिखाया गया एक्सट्रपलेशन विधि आयत विधि के लिए बिल्कुल वैसा ही काम करेगा। समलम्बाकार विधि से अंतर केवल इतना है कि जब चरण को आधा कर दिया जाता है, तो पिछली गणनाओं के परिणाम को छोड़ दिया जाता है, हालांकि, आप अंकों की संख्या को तीन गुना कर सकते हैं, और फिर अभिन्न के पिछले मूल्य का उपयोग एक नए की गणना करने के लिए भी किया जा सकता है। इस मामले में एक्सट्रपलेशन के सूत्र को एकीकरण चरणों के एक अलग अनुपात में समायोजित किया जाना चाहिए।

यहाँ से हमें सटीक नियंत्रण के साथ ट्रेपेज़ॉइड विधि के लिए निम्नलिखित कोड मिलते हैं:

 def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1): """  rtol -     nseg0 -    """ nseg = nseg0 old_ans = 0.0 dx = 1.0 * (b - a) / nseg ans = 0.5 * (func(a) + func(b)) for i in range(1, nseg): ans += func(a + i * dx) ans *= dx err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) #      #       nseg *= 2 err_est = abs(ans - old_ans) return ans

इस दृष्टिकोण के साथ, इंटीग्रैंड की गणना कई बार एक बिंदु पर नहीं की जाएगी, और सभी गणना मूल्यों को अंतिम परिणाम के लिए उपयोग किया जाता है।

लेकिन क्या समान संख्या में फ़ंक्शन गणना के साथ उच्च सटीकता प्राप्त करना संभव है? यह पता चला है कि यह संभव है, ऐसे सूत्र हैं जो एक ही ग्रिड पर ट्रेपेज़ॉइड विधि की तुलना में अधिक सटीक रूप से काम करते हैं।

टुकड़ावार परवलय सन्निकटन

अगला कदम परवलयिक तत्वों के साथ फ़ंक्शन को अनुमानित करना है। इसके लिए यह आवश्यक है कि विभाजन के खंडों की संख्या सम हो, तब एब्सिसस {( x ₀ = a , x ₁ , x ₂ ), ( x ₂ , x ₃ , x ₄ ), ... के साथ अंकों के त्रिभुज के माध्यम से परवल बनाया जा सकता है, ... ( x _{n -2} , x _{n -1} , x _n = b )}।

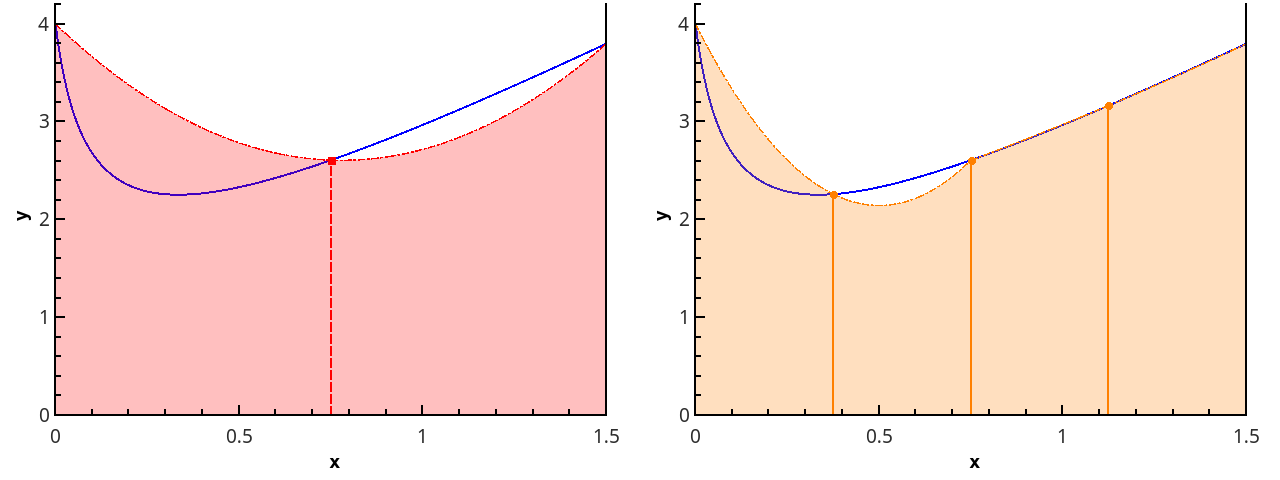
3 और 5 अंक ( एन = 2 और एन = 3) पर एक टुकड़े की परवलय सन्निकटन का चित्रण।

प्रत्येक खंड पर समारोह के अभिन्न अंग का अनुमोदन [ x _k ; x _{k +2} ] इस खंड पर परवलयिक सन्निकटन के अभिन्न अंग द्वारा और समान रूप से वितरित होने वाले बिंदुओं को मानते हुए ( x _{k +1} = x _k + h ), हम सिम्पसन सूत्र प्राप्त करते हैं :

$I_ {Simps, n} = \ sum_ {i = 0} ^ {n / 2-1} \ frac {h} {3} [f (x_ {2i}) + 4f (x_ {2i + 1}} + f (x_ {2i + 2})] = \\ = \ frac {h} {3} [f (a) + 4f (a + h) + 2f (a + 2h) + ... + 4f (bh) + f (b)] ~~ (4)$

फॉर्मूला (4) सीधे सिम्पसन विधि के "भोले" कार्यान्वयन को जन्म देता है:

स्पायलर हेडिंग

 def simpson_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" if nseg%2 = 1: nseg += 1 dx = 1.0 * (b - a) / nseg sum = (func(a) + 4 * func(a + dx) + func(b)) for i in range(1, nseg / 2): sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx) return sum * dx / 3

त्रुटि का अनुमान लगाने के लिए, आप चरण h और h / 2 के साथ इंटीग्रल की समान गणना का उपयोग कर सकते हैं - लेकिन यहां समस्या है, जब एक छोटे कदम के साथ इंटीग्रल की गणना करते हैं, तो पिछली गणना के परिणाम को त्यागना होगा, हालांकि नए फ़ंक्शन की आधी गणना पहले के समान बिंदुओं पर होगी।

सौभाग्य से, आप मशीन समय बर्बाद करने से बच सकते हैं यदि आप सिम्पसन विधि को अधिक सरल तरीके से लागू करते हैं। करीब से देखने के बाद, हम ध्यान दें कि सिम्पसन फॉर्मूले द्वारा इंटीग्रल को दो इंटीग्रल्स के माध्यम से विभिन्न चरणों के साथ ट्रैपेज़ॉइडल फॉर्मूला द्वारा दर्शाया जा सकता है। यह तीन बिंदुओं पर अभिन्न के सन्निकटन के मूल मामले में सबसे स्पष्ट रूप से देखा जाता है $(a, f_0), ~ (a + h, f_1), ~ (a + 2h, f_2)$ :

$I_ {Simps, 2} = \ frac {h} {3} (f_0 + 4f_1 + f_2) = \ frac {4} {3} h \ left (\ frac {f_0 + f_1}} [2} + \ frac { f_1 + f_2} {2} \ right) - \ frac {1} {3} \ cdot2h \ frac {f_0 + f_2} {2} = \\ = \ frac {4I_ {trap, 2} - I_ {trap, 1 }} {3}$

इस प्रकार, यदि हम चरण को आधे से कम करने की प्रक्रिया को लागू करते हैं और अंतिम दो गणनाओं को ट्रैपेज़ॉइड विधि द्वारा संग्रहीत करते हैं, तो सटीकता नियंत्रण के साथ सिम्पसन विधि को और अधिक कुशलता से लागू किया जाता है।

कुछ इस तरह ...

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #           nseg0 Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ ans = Quadrature.__restart(func, x0, x1, nseg0) old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = Quadrature.__double_nseg(func, x0, x1) err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0) new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans old_trapez_sum = new_trapez_sum new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans

समलम्बाकार और परवलय विधि की प्रभावशीलता की तुलना करें:

 >>> import math >>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 65537 4.250000001385811 >>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 2049 4.2500000000490985

जैसा कि आप देख सकते हैं, दोनों विधियों के साथ उत्तर काफी उच्च सटीकता के साथ प्राप्त किया जा सकता है, लेकिन इंटीग्रैंड के लिए कॉल की संख्या बहुत अलग है - एक उच्च क्रम विधि 32 गुना अधिक कुशल है!

एकीकरण त्रुटि बनाम चरणों की संख्या को प्लॉट करके, हम यह सत्यापित कर सकते हैं कि सिम्पसन फॉर्मूला का अनुमानित क्रम चार है, अर्थात्। संख्यात्मक एकीकरण त्रुटि $| I_ {Simps, n} - I | = O (1 / n ^ 4)$ (और इस सूत्र का उपयोग करने वाले क्यूबिक बहुपद के अभिन्न किसी भी n > 0 के लिए गोलाई त्रुटियों तक की गणना की जाती है।)

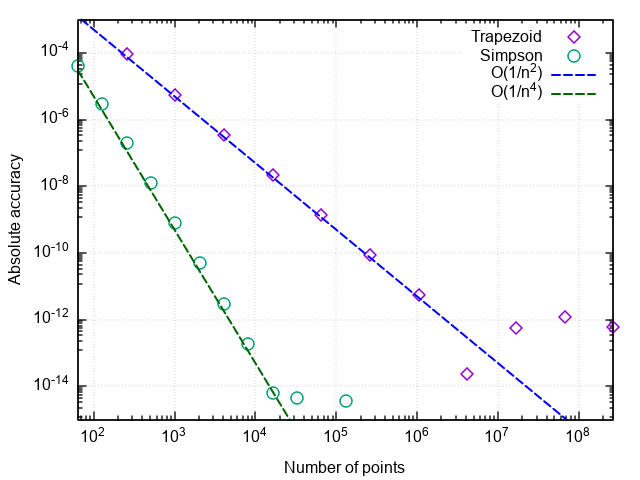
इसलिए, इस तरह की दक्षता में वृद्धि सरल ट्रेपोज़ॉइड फॉर्मूला की तुलना में उत्पन्न होती है।

आगे क्या है?

द्विघात सूत्र की सटीकता में वृद्धि का अगला तर्क आम तौर पर समझा जा सकता है - अगर हम कभी-कभी उच्च डिग्री के बहुपद के साथ फ़ंक्शन को अनुमानित करना जारी रखते हैं, तो इन बहुपद की अभिन्नता मूल फ़ंक्शन से अभिन्न रूप से अधिक सटीक रूप से अनुमानित होगी। इस दृष्टिकोण को द्विघात न्यूटन-कोट्स सूत्र का निर्माण कहा जाता है। 8 सन्निकटन आदेश तक के सूत्र ज्ञात हैं, लेकिन वैकल्पिक शब्द भारांक गुणांक w _{i i} in (2) के बीच प्रकट होते हैं, और सूत्र गणना में स्थिरता खो देते हैं।

दूसरे तरीके से कोशिश करते हैं। द्विघात सूत्र की त्रुटि को एकीकरण चरण एच की शक्तियों में एक श्रृंखला के रूप में दर्शाया गया है। ट्रेपेज़ॉइड विधि की एक उल्लेखनीय संपत्ति (और एक मिडपॉइंट के साथ आयताकार!) है कि इसके लिए इस श्रृंखला में केवल डिग्री शामिल हैं:

$I_ {जाल, n} [f, a, b] = \ int_a ^ bf (x) dx + C_2h ^ 2 + C_4h ^ 4 + C_6h ^ 6 + ..., ~ h = \ _rac {ba} {n } ~~~ (5)$

रिचर्डसन एक्सट्रपलेशन इस विस्तार के क्रमिक अनुमान लगाने पर आधारित है: एक बहुपद द्वारा इंटीग्रेट करने की बजाय अभिन्न की गणना अनुमानों से $I (h)$ एक बहुपद सन्निकटन का निर्माण किया जाता है, जो h = 0 के लिए अभिन्न के वास्तविक मूल्य को सर्वोत्तम सन्निकटन देना चाहिए।

विभाजन कदम की भी शक्तियों में एकीकरण त्रुटि का विस्तार तेजी से एक्सट्रपलेशन के अभिसरण को तेज करता है, क्योंकि आदेश 2 एन के सन्निकटन के लिए, ट्रैपोज़ाइड विधि द्वारा अभिन्न के केवल एन मान की आवश्यकता होती है।

यदि हम मानते हैं कि प्रत्येक बाद की अवधि पिछले एक से कम है, तो हम क्रमिक रूप से एच की डिग्री को बाहर कर सकते हैं, विभिन्न चरणों के साथ अभिन्न सन्निकटन की गणना कर रहे हैं। चूंकि उपरोक्त कार्यान्वयन आसानी से हमें विभाजन को आधे में विभाजित करने की अनुमति देता है, इसलिए चरण एच और एच / 2 के लिए सूत्रों पर विचार करना सुविधाजनक है।

$I_ {जाल, n} - I \ लगभग C_2h ^ 2; ~ I_ {जाल, 2n} - I \ लगभग C_2 \ left (\ frac {h} {2} \ right) ^ 2$

यह दिखाना आसान है कि ट्रेपोज़ॉइड फॉर्मूले की त्रुटि के वरिष्ठ शब्द का अपवाद बिल्कुल सिम्पसन फॉर्मूला देगा:

$I = I_ {जाल, 2n} - C_2 \ बाएँ (\ frac {h} {2} \ right) ^ 2 + O (h ^ 4) \ लगभग I_ {जाल, 2n} - \ frac {{_ {जाल}, 2n} -I_ {जाल, n}} {1-2 ^ 2} = I_ {Simps, 2n}$

सिम्पसन फार्मूले के लिए इसी तरह की प्रक्रिया को दोहराते हुए, हम प्राप्त करते हैं:

$I_ {Simps, 2n} - I \ लगभग C_4 \ left (\ frac {h} {2} \ right) ^ 4; ~ I_ {Simps, n} - I \ लगभग C_4h ^ 4$

$I = I_ {Simps, 2n} - C_4 \ left (\ frac {h} {2} \ right) ^ 4 + O (h ^ 6) \ लगभग I_ {Simps, 2n} - \ frac / I_ {Simps, 2n} -I_ {Simps, n}} {1-2 ^ 4}$

यदि आप जारी रखते हैं, तो निम्न तालिका करघे:

2 आदेश	4 आदेश	6 आदेश
मैं _0,0
मैं _१.०	मैं _1,1
मैं _२.०	मैं _२.१	मैं _2.2
...	...	...

पहले कॉलम में ट्रैपोज़ाइडल विधि द्वारा गणना की गई इंटीग्रल शामिल हैं। शीर्ष पंक्ति से नीचे जाने पर, खंड का विभाजन दो बार छोटा हो जाता है, और बाएं स्तंभ से दाईं ओर बढ़ने पर, इंटीग्रल बढ़ के सन्निकटन का क्रम बढ़ता है (यानी, दूसरे कॉलम में सिम्पसन विधि द्वारा इंटीग्रल शामिल हैं, आदि)।

तालिका के तत्व, जैसा कि विस्तार (5) से घटाया जा सकता है, पुनरावृत्ति संबंध से संबंधित हैं:

$I_ {i, j} = I_ {i, j-1} - \ frac {I_ {i, j-1} -I_ {i-1, j-1}} {1- \ left (\ frac {h_) {Ij}} {h_i} \ right) ^ 2} = I_ {i, j-1} - \ frac {I_ {i, j-1} -I_ {i-1, j-1}} {1-2 ^ {2 जे}} ~~~ (6)$

अभिन्न के सन्निकटन की त्रुटि का अनुमान एक पंक्ति में विभिन्न आदेशों के सूत्रों के अंतर से लगाया जा सकता है, अर्थात्।

$\ Delta_ {i, j} \ अनुमानित I_ {i, j} - I_ {i, j-1 "$

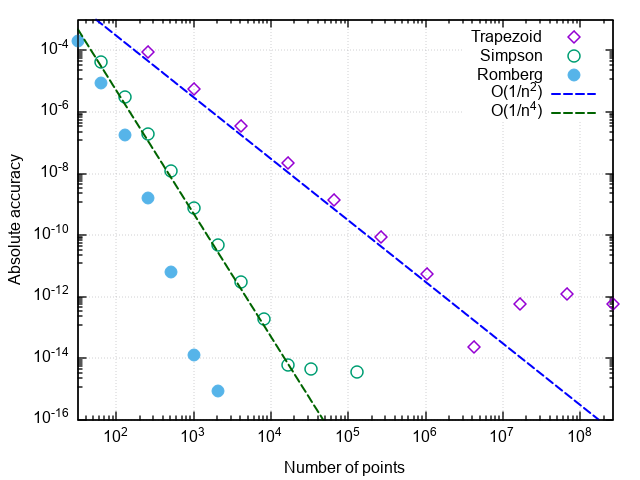
ट्रेपोज़ॉइड एकीकरण के साथ रिचर्डसन एक्सट्रपलेशन के उपयोग को रोमबर्ग विधि कहा जाता है । यदि सिम्पसन विधि ट्रैपेज़ॉइडल विधि द्वारा दो पिछले मूल्यों को ध्यान में रखती है, तो रोमबर्ग विधि इंटीग्रल का अधिक सटीक अनुमान प्राप्त करने के लिए ट्रैपोज़ाइडल विधि द्वारा पहले गणना की गई सभी मानों का उपयोग करती है।

कार्यान्वयन

एक अतिरिक्त विधि द्विघात वर्ग में जोड़ी जाती है

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #          nseg0  Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True): """   nseg0 -     maxcol -   """ #   Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]] i = 0 maxcol = max(0, maxcol) ans = Itable[i][i] error_est = max(1, abs(ans)) while (error_est > abs(rtol * ans)): old_ans = ans i += 1 d = 4.0 ans_col = min(i, maxcol) Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1)) for j in range(0, ans_col): diff = Itable[i][j] - Itable[i - 1][j] Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0) d *= 4.0 ans = Itable[i][ans_col] if (maxcol <= 1): #       error_est = abs(ans - Itable[i - 1][-1]) elif (i > maxcol): error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)]) else: error_est = abs(ans - Itable[i - 1][i - 1]) print("Total function calls: " + str(Quadrature.__ncalls)) return ans

आइए देखें कि उच्च-क्रम सन्निकटन कैसे काम करता है:

 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) #  Total function calls: 65537 4.250000001385811 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) #  Total function calls: 2049 4.2500000000490985 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4) Total function calls: 257 4.250000001644076

हम आश्वस्त हैं कि, पैराबोला विधि की तुलना में, इंटीग्रैंड के लिए कॉल की संख्या में 8 गुना की कमी आई है। आवश्यक सटीकता में और वृद्धि के साथ, रोमबर्ग विधि के फायदे और भी स्पष्ट हो जाते हैं:

कुछ नोट

टिप्पणी 1. इन समस्याओं में फ़ंक्शन कॉल की संख्या अभिन्न की गणना करते समय रकम की संख्या को दर्शाती है। इंटीग्रैंड की गणना की संख्या को कम करने से न केवल कंप्यूटिंग संसाधनों को बचाया जाता है (हालांकि यह एक अधिक अनुकूलित कार्यान्वयन के मामले में भी है), लेकिन परिणाम पर राउंडिंग त्रुटियों के प्रभाव को भी कम करता है। इसलिए, जब आप परीक्षण फ़ंक्शन के अभिन्न की गणना करने की कोशिश करते हैं, तो ट्रैपोज़ॉइड विधि जमा करती है जब आप 5 × 10 ^{-15 के} सापेक्ष सटीकता को प्राप्त करने की कोशिश करते हैं, तो पैराबोला विधि - 2 × 10 ^-16 की वांछित सटीकता (जो दोहरी सटीक संख्या की सीमा है) के साथ, और रोमबर्ग विधि गणना के साथ मुकाबला करती है। मशीन सटीकता के साथ अभिन्न परीक्षण (कम बिट त्रुटि के साथ)। यही है, न केवल फ़ंक्शन कॉल की संख्या के लिए एकीकरण की सटीकता बढ़ जाती है, बल्कि अभिन्न की गणना की अधिकतम प्राप्त सटीकता भी होती है।

टिप्पणी 2. यदि विधि एक निश्चित सटीकता निर्दिष्ट करने पर परिवर्तित हो जाती है, तो इसका मतलब यह नहीं है कि अभिन्न के परिकलित मूल्य में समान सटीकता है। सबसे पहले, यह उन मामलों पर लागू होता है जब निर्दिष्ट त्रुटि मशीन सटीकता के करीब होती है।

टिप्पणी 3. यद्यपि कई कार्यों के लिए रोमबर्ग विधि लगभग जादुई तरीके से काम करती है, लेकिन यह मानती है कि इंटीग्रैंड ने उच्च आदेशों के व्युत्पन्न को बाध्य किया है। इसका मतलब है कि किन्क्स या ब्रेक के साथ कार्यों के लिए, यह सरल तरीकों से भी बदतर हो सकता है। उदाहरण के लिए, f ( x ) = को एकीकृत करें x |:

 >>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5) Total function calls: 9 5.0 >>> Quadrature.simpson(abs, -1, 3, rtol=1e-5) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3) Total function calls: 33 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4) Total function calls: 33 5.000001383269357

टिप्पणी 4. ऐसा प्रतीत हो सकता है कि उच्चतर सन्निकटन क्रम, बेहतर होगा। वास्तव में, रोमबर्ग तालिका में स्तंभों की संख्या को 4-6 तक सीमित करना बेहतर है। इसे समझने के लिए, सूत्र (6) देखें। दूसरा शब्द j -1th कॉलम के दो लगातार तत्वों का अंतर है जो लगभग 4 ^{j से} विभाजित है। क्योंकि j -th कॉलम में क्रम 2 j का एक अभिन्न अंग होता है, फिर अंतर स्वयं (1 / n _i ) ^{2 j} ~ 4 ^{- ij} के क्रम का होता है। विभाजन को ध्यान में रखते हुए, ~ 4 ^{- ( i +1) j} ~ 4 ^{- j ²} प्राप्त किया जाता है। यानी j ~ 7 के लिए, (6) में दूसरा शब्द फ़्लोटिंग-पॉइंट संख्याओं को जोड़ने पर आदेशों की कमी के बाद सटीकता खो देता है, और सन्निकटन क्रम में वृद्धि गोलाई त्रुटियों के संचय को जन्म दे सकती है।

टिप्पणी 5. इच्छुक पक्ष ब्याज के लिए अभिन्न को खोजने के लिए वर्णित विधियों का उपयोग कर सकते हैं। $\ int_0 ^ 1 \ sqrt {x} \ sin {x} dx$ और उसके बराबर $\ int_0 ^ 1 2t ^ 2 \ sin {t ^ 2} dt$ । जैसा कि वे कहते हैं, अंतर महसूस करते हैं।

निष्कर्ष

एक समान ग्रिड पर कार्यों के संख्यात्मक एकीकरण के बुनियादी तरीकों का विवरण और कार्यान्वयन प्रस्तुत किया गया है। यह प्रदर्शित किया जाता है कि कैसे, एक सरल संशोधन का उपयोग करते हुए, ट्रेपोज़ॉइड पद्धति के आधार पर रोमबर्ग विधि का उपयोग करके चतुर्भुज सूत्रों के वर्ग को प्राप्त किया जाता है, जो संख्यात्मक एकीकरण के अभिसरण को तेज करता है। विधि "साधारण" कार्यों को एकीकृत करने के लिए अच्छी तरह से काम करती है, अर्थात्। एकीकरण के अंतराल पर कमजोर रूप से भिन्न, खंड के किनारों पर कोई विलक्षणता नहीं है (देखें रेमार्क 5), तेजी से दोलन, आदि।

( [3] — C++).

.. , .. . . .: . 1989.
J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
WH Press, SA Teukolsky, WT Vetterling, BP Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.

निश्चित इंटीग्रल्स की गणना: बुनियादी एल्गोरिदम

अभिन्न की परिभाषा

चतुर्भुज सूत्र

कम्प्यूटेशनल कार्य

टुकड़े टुकड़े निरंतर सन्निकटन

टुकड़े-टुकड़े रैखिक सन्निकटन

गणना सटीकता नियंत्रण

टुकड़ावार परवलय सन्निकटन

आगे क्या है?

कुछ नोट

निष्कर्ष

More articles: