छुपाये बिना छुप जाना। एक बार फिर एलएसबी स्टेग्नोग्राफ़ी, ची-स्क्वायर और ... विलक्षणता के बारे में?

आज, हम फिर से पुराने घोंसले को चालू करेंगे और इस बारे में बात करेंगे कि बिल्ली के साथ तस्वीर में बिट्स का एक गुच्छा कैसे छिपाया जाए, कई उपलब्ध उपकरणों को देखें और सबसे लोकप्रिय हमलों का विश्लेषण करें। और यह प्रतीत होता है, इसके साथ क्या विलक्षणता है?

जैसा कि वे कहते हैं, यदि आप किसी चीज़ का पता लगाना चाहते हैं, तो इसके बारे में एक लेख हबर पर लिखें! (सावधानी, बहुत सारा पाठ और चित्र)



स्टेग्नोग्राफ़ी (शाब्दिक रूप से ग्रीक "क्रिप्टोग्राफ़ी") डेटा ट्रांसफर के तथ्य को छिपाते हुए अन्य खुले डेटा (स्टेगोकॉनटेनर्स) में छिपे हुए डेटा (स्टीगो मैसेजेस) को प्रसारित करने का विज्ञान है। सतर्क न हों, वास्तव में, सब कुछ इतना जटिल नहीं है।

तो, जहां छवि में आप संदेश छिपा सकते हैं ताकि कोई नोटिस न करे?

और केवल दो स्थान हैं: मेटाडेटा और स्वयं छवि। उत्तरार्द्ध काफी सरल है, बस Google पर "exif" टाइप करें। तो चलिए अब शुरू करते हैं दूसरे के साथ।

कम से कम महत्वपूर्ण बिट

सबसे लोकप्रिय रंग मॉडल आरजीबी है, जहां रंग को तीन घटकों के रूप में दर्शाया जाता है: लाल, हरा और नीला । प्रत्येक घटक को 8 बिट्स का उपयोग करके शास्त्रीय संस्करण में एन्कोड किया गया है, अर्थात यह 0 से मान ले सकता है
255. यह यहाँ है कि कम से कम महत्वपूर्ण बिट छुपाता है। यह समझना महत्वपूर्ण है कि एक आरजीबी रंग ऐसे तीन बिट्स के लिए खाता है।

उन्हें और अधिक स्पष्ट रूप से प्रस्तुत करने के लिए, हम छोटे जोड़तोड़ करेंगे।

जैसा कि वादा किया गया था, पीएनजी प्रारूप में एक बिल्ली की तस्वीर लें।



हम इसे तीन चैनलों में विभाजित करते हैं और प्रत्येक चैनल में हम कम से कम महत्वपूर्ण बिट लेते हैं। तीन नई छवियां बनाएं, जहां प्रत्येक पिक्सेल NZB के लिए खड़ा हो। शून्य - पिक्सेल सफेद है, इकाई क्रमशः काला है।

हमें यह मिलता है।




लेकिन, एक नियम के रूप में, छवि "इकट्ठे रूप में" पाई जाती है। एक छवि में तीन घटकों के एनजेडबी का प्रतिनिधित्व करने के लिए, यह एक पिक्सेल में घटक को बदलने के लिए पर्याप्त है जहां एनजेडबी एकता है, इसे 255 के साथ बदलें, और अन्यथा इसे 0 से बदलें।

लेकिन कोई कम महत्वपूर्ण नहीं है

कल्पना कीजिए कि पिछली तस्वीर में हमने जो कुछ भी देखा था वह हमारा है और हमें इसके साथ कुछ भी करने का अधिकार है। फिर हम इसे बिट्स की एक धारा के रूप में लेते हैं, जहां से हम पढ़ सकते हैं और जहां हम लिख सकते हैं।

हम उस डेटा को लेते हैं जिसे हम छवि में अंतर करना चाहते हैं, उन्हें बिट्स के रूप में पेश करते हैं और मौजूदा वाले के स्थान पर उन्हें लिखते हैं।

इस डेटा को निकालने के लिए, हम NZB को एक बिटस्ट्रीम के रूप में पढ़ते हैं और इसे वांछित रूप में लाते हैं। यह जानने के लिए कि एक नियम के रूप में, कितने बिट्स को गिनने की आवश्यकता है, संदेश का आकार शुरुआत में लिखा गया है। लेकिन ये कार्यान्वयन विवरण हैं।

यह ध्यान दिया जाना चाहिए कि लगभग 50% मामलों में, जिस बिट को हम लिखना चाहते हैं और तस्वीर में बिट संयोग होगा और हमें कुछ भी बदलना नहीं होगा।

बस, यहीं विधि समाप्त होती है।

यह काम क्यों करता है?

नीचे दी गई छवियों पर एक नज़र डालें।

यह एक खाली स्टीगोकैनटेनर है:



और यह 95% पूर्ण है:



अंतर देखें? लेकिन वह है ऐसा क्यों?

आइए दो रंगों को देखें: (0, 0, 0) और (1, 1, 1), अर्थात प्रत्येक घटक में NZB द्वारा अलग-अलग रंग।



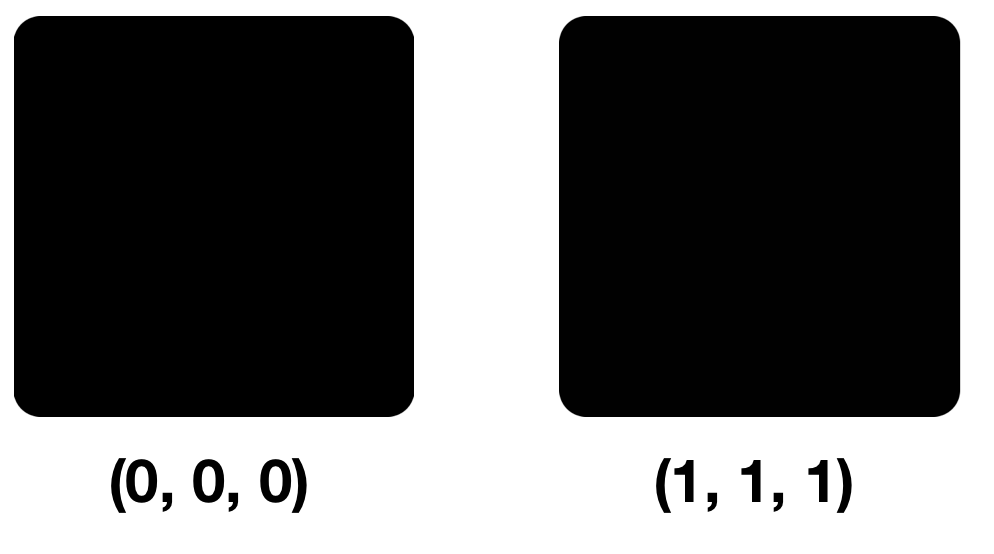
पहली, दूसरी और तीसरी नज़र में पिक्सेल में थोड़ा अंतर ध्यान देने योग्य नहीं होगा। तथ्य यह है कि हमारी आंख लगभग 10 मिलियन रंगों को भेद कर सकती है, और मस्तिष्क केवल लगभग 150 है। RGB मॉडल में 16,777,216 रंग भी शामिल हैं। आप यहां उन सभी को अलग करने की कोशिश कर सकते हैं।

कमांड लाइन से

कई खुले स्रोत कमांड लाइन उपकरण उपलब्ध नहीं हैं जो एलएसबी स्टेग्नोग्राफ़ी का प्रतिनिधित्व करते हैं।

सबसे लोकप्रिय नीचे दी गई तालिका में पाया जा सकता है।

बिल्ली कहाँ है?

और एलएसबी स्टेग्नोग्राफ़ी पर हमलों की सूची में पहला दृश्य आक्रमण है। अजीब लगता है, है ना? सब के बाद, एक गुप्त के साथ बिल्ली ने पहली नज़र में एक भरा स्टीग कंटेनर के रूप में खुद को धोखा नहीं दिया। हम्म् ... आपको बस यह जानना होगा कि कहाँ देखना है। यह अनुमान लगाना आसान है कि केवल एनजेडबी हमारे करीब ध्यान देने योग्य है।

एक भरे हुए स्टीगोकॉनटेनर के लिए, NZB के साथ की छवि इस प्रकार है:



विश्वास नहीं होता? यहां आपके पास अलग-अलग तीनों चैनलों से NZB हैं:




यह एक "ड्राइंग" है जो एनजेडबी में संदेश को छिपाने के लिए विशिष्ट है। पहली नज़र में, यह एक साधारण शोर की तरह लगता है। लेकिन विचार करते समय संरचना दिखाई देती है। यहां आप देख सकते हैं कि स्टेगोकॉनटेनर भरा हुआ है। यदि हम एक गरीब बिल्ली की क्षमता का 30% पर संदेश लेते हैं, तो हमें यह चित्र मिलेगा:


उनका NZB:



~ 70% बिल्ली अपरिवर्तित रहती है।

यहां यह एक छोटे से विषयांतर करने और आकारों के बारे में बात करने के लायक है। 30% बिल्ली क्या है? बिल्ली का आकार 603x433 पिक्सेल है। इस आकार का 30% 78459 पिक्सेल है। प्रत्येक पिक्सेल में 3 बिट्स की जानकारी होती है। कुल 78459 3 = 235377 बिट्स या 30 किलोबाइट से थोड़ा कम 30% सील में फिट बैठता है। और पूरी बिल्ली में लगभग 100 किलोबाइट फिट होंगे। ऐसी बातें।

लेकिन हम यहां आपके लिए एक कारण से हैं। फिर आँखों को धोखा देने के लिए कैसे?
पहले सोचा: संदेश को शोर में चिपका दें। लेकिन यह वहां नहीं था। अगला भरा हुआ स्टीगोकॉनटेनर और उसके एलएसबी का एक टुकड़ा है।



थोड़े प्रयास से, हम अभी भी एक परिचित संरचना को समझ सकते हैं। आशा मत हारो, सज्जनों!

ही हे हे

बहुत सी चीजें आंकड़ों को तोड़ती हैं, आप जानते हैं।

तस्वीर में कुछ बदलते हुए, हम इसके सांख्यिकीय गुणों को बदलते हैं। विश्लेषक के लिए यह इन परिवर्तनों को ठीक करने का एक तरीका खोजने के लिए पर्याप्त है।

अच्छे पुराने ची-स्क्वायर की शुरुआत एंड्रेस वेसफील्ड और एंड्रियास पफिट्जमैन ने ड्रेसडेन विश्वविद्यालय के अपने काम "स्टेग्नोग्राफ़िक सिस्टम्स पर हमलों" से की थी, जो यहां पाया जा सकता है।

इसके बाद, हम एक ही रंग के विमान के भीतर या RGB के संदर्भ में, एक चैनल पर हमलों के बारे में बात करेंगे। प्रत्येक हमले के परिणाम औसत से कम हो सकते हैं और "इकट्ठे" छवि के लिए परिणाम प्राप्त कर सकते हैं।

तो, ची-स्क्वायर का हमला इस धारणा पर आधारित है कि खाली स्टीगोकॉनटेनर में पड़ोसी (कम से कम महत्वपूर्ण बिट द्वारा रंग) (मूल्यों की जोड़ी) की एक साथ उपस्थिति की संभावना बेहद छोटी है। यह वास्तव में है, आप इस पर विश्वास कर सकते हैं। दूसरे शब्दों में, खाली कंटेनर के लिए दो आसन्न रंगों के पिक्सेल की संख्या काफी भिन्न होती है। हमें केवल प्रत्येक रंग के पिक्सेल की संख्या की गणना करना है और कुछ सूत्रों को लागू करना है। वास्तव में, ची-स्क्वायर परीक्षण का उपयोग करके एक परिकल्पना का परीक्षण करना एक सरल कार्य है।

थोड़ा गणित?

आइए अध्ययन के तहत छवि में आई-वें रंग के पिक्सल की संख्या वाले i-वें स्थान पर एक सरणी हो।

तब:

1. मापा रंग आवृत्ति $$$i = 2k$ :
   

   $$

   $$n_k = h [2k], [0, 127] में ~ k,$$
   
   
2. सैद्धांतिक रूप से अपेक्षित रंग आवृत्ति $$$i = 2k$ :
   

   $$

   $$n_k ^ * = \ frac {h [2k] + h [2k + 1]} {2}, ~ k \ _ [0,127] में$$
   
   

इसे पायथन में अनुवाद करने से कुछ इस तरह का उत्पादन होगा:

for k in range(0, len(histogram) // 2): expected.append(((histogram[2 * k] + histogram[2 * k + 1]) / 2)) observed.append(histogram[2 * k]) 

जहां चित्र में हिस्टोग्राम रंग के पिक्सेल की संख्या है, $$$i \ _ [0, 255] $ मे$

स्वतंत्रता के -1 की डिग्री की संख्या के लिए ची-स्क्वायर मानदंड की गणना निम्नानुसार की जाती है (k विभिन्न रंगों की संख्या है, अर्थात 256):

$$

$$\ chi_ {k-1} ^ 2 = \ sum_ {i = 1} ^ {k} \ frac {(n_k - n_k ^ *) ^ 2} {n_k ^ *};$$

और अंत में, पी संभावना है कि वितरण $$$n_i$ और $$$n_i ^ *$ इन शर्तों के तहत वे समान हैं (संभावना है कि हमारे पास एक भरा हुआ स्टीगोकॉनटेनर है)। यह चिकनाई समारोह को एकीकृत करके गणना की जाती है:

$$

$$P = 1 - \ frac {1} {2 ^ {\ frac {k-1} {2}} \ Gamma (\ frac {k-1} {2})} \ int_0 ^ {\ chi_ {k-1 } ^ 2} e ^ {- \ frac {x} {2}} x ^ {\ frac {k-1} {2} -1} dx;$$

ची-स्क्वायर को पूरी छवि पर लागू करना सबसे प्रभावी है, लेकिन केवल इसके भागों के लिए, उदाहरण के लिए, लाइनों के लिए। यदि लाइन के लिए गणना की संभावना 0.5 से अधिक है, तो लाल रंग के साथ मूल छवि में लाइन भरें। यदि कम है, तो हरा। 30% परिपूर्णता के साथ एक बिल्ली के लिए, चित्र इस प्रकार दिखेगा:



काफी सही है, है ना?

ठीक है, हमें गणितीय रूप से ध्वनि का दौरा पड़ा, आप गणित को धोखा नहीं दे सकते! या… ??

शफ़ल डांस

यह विचार काफी सरल है: बिट्स क्रम में नहीं, बल्कि यादृच्छिक स्थानों पर लिखें। ऐसा करने के लिए, आपको पीआरएसपी लेने की आवश्यकता है, उसी पक्ष (उर्फ पासवर्ड) के साथ एक ही यादृच्छिक स्ट्रीम जारी करने के लिए इसे कॉन्फ़िगर करें। पासवर्ड को जाने बिना, हम PRNG को कॉन्फ़िगर नहीं कर पाएंगे और उस पिक्सेल को खोज पाएंगे जिसमें संदेश छिपा है। हम इसका परीक्षण एक बिल्ली पर करेंगे।

बिल्ली का बच्चा (32% पूरा):



उसका एलएसबी:



तस्वीर शोर करती है, लेकिन अनुभवहीन विश्लेषक के लिए संदिग्ध नहीं है। ची-स्क्वायर क्या कहता है?


ऐसा लगता है कि काली टोपी जीती है? कोई फर्क नहीं पड़ता कि कैसे ...

नियमितता-व्यक्तित्व

एक अन्य सांख्यिकीय पद्धति 2001 में जेसिका फ्रेडरिक, मिरोस्लाव गोल्यान और एंड्रियास Pfitzman थी। इसे RS विधि के रूप में नामित किया गया था। मूल लेख यहां लिया जा सकता है।

विधि में कई प्रारंभिक चरण होते हैं।

छवि को एन पिक्सल के समूहों में विभाजित किया गया है। उदाहरण के लिए, लगातार 4 पिक्सेल। एक नियम के रूप में, ऐसे समूहों में आसन्न पिक्सेल होते हैं।
लाल चैनल में अनुक्रमिक भरने के साथ हमारी बिल्ली के लिए, पहले पांच समूह होंगे:

• [78, 78, 79, 78]
  
• [78, 78, 78, 78]
  
• [78, 79, 78, 79]
  
• [79, 76, 79, 76]
  
• [76, 76, 76, 77]
  

(सभी माप आरजीबी के क्लासिक संस्करण में हैं)

फिर हम तथाकथित भेदभावपूर्ण फ़ंक्शन या चिकनाई फ़ंक्शन को परिभाषित करते हैं, जो प्रत्येक समूह के पिक्सेल को एक वास्तविक संख्या में मैप करता है। इस फ़ंक्शन का उद्देश्य पिक्सेल समूह जी की निर्मलता या "नियमितता" को कैप्चर करना है $$$G = (x_1, ..., x_n)$ , जितना महत्वपूर्ण भेदभावपूर्ण कार्य होगा। अधिकतर, पिक्सल के एक समूह का "भिन्नता" चुना जाता है, या, अधिक सरलता से, एक समूह में पड़ोसी पिक्सल के अंतर का योग। लेकिन यह भी छवि के बारे में सांख्यिकीय मान्यताओं को ध्यान में रख सकता है।

$$

$$f (x_1, x_2, ..., x_n) = \ sum_ {i = 1} ^ {n-1} | x_ {i + 1} - x_i |$$

हमारे उदाहरण से पिक्सेल के समूह के लिए चिकनाई के कार्य का मान:

• f (78, 78, 79, 78) = 2
• f (78, 78, 78, 78) = 0
• f (78, 79, 78, 79) = 3
• f (79, 76, 79, 76) = 9
• f (76, 76, 76, 77) = 1

अगला, एक पिक्सेल से फ़्लिपिंग फ़ंक्शन का वर्ग निर्धारित किया जाता है।

उनमें कुछ गुण होने चाहिए।

$$

$$1. ~~~ \ forall x \ P में: ~ F (F (x)) = x, ~~ P = \ {0, ~ 255 \};$$

$$

$$2. ~~~ F_1: 0 \ leftrightarrow 1, ~ 2 \ leftrightarrow 3, ~ ..., 254 \ leftrightarrow 255 ;$$

$$

$$3 ~~~ \ forall x \ _ in P: ~ F _ {- 1} (x) = F_1 (x + 1) -1 - $$$

जहाँ $$$एफ$ - एक वर्ग से कोई भी कार्य, $$$F_1$ एक प्रत्यक्ष फ़्लिपिंग फ़ंक्शन है, और $$$F _ {- 1}$ - उल्टा। इसके अलावा, समान फ़्लिपिंग फ़ंक्शन को आमतौर पर चिह्नित किया जाता है $$$F_0$ जो पिक्सेल नहीं बदलता है।

अजगर फ़्लिपिंग फ़ंक्शंस कुछ इस तरह दिख सकते हैं:

 def flip(val): if val & 1: return val - 1 return val + 1 def invert_flip(val): if val & 1: return val + 1 return val - 1 def null_flip(val): return val 

पिक्सेल के प्रत्येक समूह के लिए, हम फ़्लिपिंग फ़ंक्शंस में से एक को लागू करते हैं और फ़्लिपिंग से पहले और बाद में विभेदक फ़ंक्शन के मूल्य के आधार पर, हम पिक्सेल समूह के प्रकार का निर्धारण करते हैं: सामान्य ( आर एग्युलर), एकल / असामान्य ( एस इंगुलर), और बेकार बेकार। चूंकि बाद के प्रकार का उपयोग आगे नहीं किया जाता है, इसलिए कुंजी प्रकारों के पहले अक्षरों के बाद विधि का नाम दिया गया था। यह नाम का पूरा रहस्य है, विलक्षणता का इससे कोई लेना-देना नहीं है :)



हम अलग-अलग पिक्सेल में अलग-अलग फ़्लिपिंग लागू करना चाह सकते हैं , इसके लिए हम -1, 0 या 1 के एन वैल्यू वाले मास्क M को परिभाषित करते हैं।

$$

$$F_M (G) = (F_ {M (1)} (x_1), F_ {M (2)} (x_2), ..., F_ {M (n)} (x_n)$$

हमारे उदाहरण के लिए मुखौटा शास्त्रीय होने दें - [1, 0, 0, 1]। यह प्रायोगिक रूप से पाया गया कि सममित मास्क जिसमें शामिल नहीं है $$$F _ {- 1}$ । इसके अलावा सफल विकल्प होंगे: [0, 1, 0, 1], [0, 1, 1, 0], [1, 0, 1, 0]। हम उदाहरण के लिए समूहों से फ़्लिपिंग लागू करते हैं, चिकनाई मान की गणना करते हैं और पिक्सेल समूह के प्रकार का निर्धारण करते हैं:

• $$$F_m$ (78, 78, 79, 78) = [79, 78, 79, 79];
  f (79, 78, 79, 79) = 2 = 2 = f (78, 78, 79, 78)
  अनुपयोगी समूह
  
  
• $$$F_m$ (78, 78, 78, 78) = [79, 78, 78, 79];
  f (79, 78, 78, 79) = 2> 0 = f (78, 78, 78, 78)
  नियमित समूह
  
  
• $$$F_m$ (78, 79, 78, 79) = [79, 79, 78, 78];
  f (79, 79, 78, 78) = 1 <3 = f (78, 79, 78, 79) एकवचन समूह
  
  
• $$$F_m$ (79, 76, 79, 76) = [78, 76, 79, 77];
  f (78, 76, 79, 77) = 7 <9 = f (79, 76, 79, 76) एकवचन समूह
  
  
• $$$F_m$ (76, 76, 76, 77) = [77, 76, 76, 76];
  एफ (77, 76, 76, 76) = 1 = 1 = एफ (76, 76, 76, 77)
  अनुपयोगी समूह
  
  

हम मास्क M के लिए नियमित समूहों की संख्या को निरूपित करते हैं $$$R_M$ (सभी समूहों के प्रतिशत में), और $$$S_M$ एकवचन समूहों के लिए।

तो $$$R_M + S_M \ leq 1$ और $$$R _ {- M} + S _ {- M} \ leq 1$ , एक नकारात्मक मुखौटा के लिए (सभी मुखौटा घटकों को -1 से गुणा किया जाता है), क्योंकि $$$R_M + S_M + U_M = 1$ जब $$$U_M$ खाली हो सकता है। इसी तरह एक नकारात्मक मुखौटा के लिए।

मुख्य सांख्यिकीय परिकल्पना है कि एक विशिष्ट छवि में अपेक्षित मूल्य $$$R_M$ के बराबर है $$$R _ {- M}$ , और उसी के लिए सच है $$$S_M$ और $$$S _ {- M}$ । यह प्रायोगिक डेटा और फ़्लिपिंग फ़ंक्शन की अंतिम संपत्ति के चारों ओर एक टैम्बोरिन के साथ कुछ नृत्य द्वारा साबित होता है।

$$

$$R_M \ cong S_M ~~~~ R _ {- M} \ cong S _ {- M 2$$

आइए इसे हमारे छोटे उदाहरण पर देखें? छोटे नमूने के आकार को देखते हुए, हम इस परिकल्पना की पुष्टि नहीं कर सकते हैं। आइए देखें कि उल्टे मास्क के साथ क्या होता है: [-1, 0, 0, -1]।

• F_M (78, 78, 79, 78) = [77, 78, 79, 77];
  f (77, 78, 79, 77) = 4> 2 = f (77, 78, 79, 77)
  नियमित समूह
  
  
• F_M (78, 78, 78, 78) = [77, 78, 78, 77];
  f (77, 78, 78, 77) = 2> 0 = f (78, 78, 78, 78)
  नियमित समूह
  
  
• F_M (78, 79, 78, 79) = [77, 79, 78, 80];
  f (77, 79, 78, 80) = 5> 3 = f (78, 79, 78, 79)
  नियमित समूह
  
  
• F_M (79, 76, 79, 76) = [80, 76, 79, 75];
  f (80, 76, 79, 75) = 11> 9 = f (79, 76, 79, 76)
  नियमित समूह
  
  
• F_M (76, 76, 76, 77) = [75, 76, 76, 78];
  f (75, 76, 76, 78) = 3> 1 = f (76, 76, 76, 77)
  नियमित समूह
  
  

खैर, सब कुछ स्पष्ट है।

हालाँकि के बीच का अंतर $$$R_M$ और $$$S_M$ एम्बेडेड संदेश की लंबाई मीटर बढ़ने के साथ शून्य हो जाता है और हमें वह मिल जाता है $$$R_M \ cong S_M$ ।

यह हास्यास्पद है कि एलएसबी विमान के यादृच्छिककरण पर विपरीत प्रभाव पड़ता है $$$R _ {- M}$ और $$$S _ {- M}$ । एम्बेडेड संदेश की लंबाई मीटर के साथ उनका अंतर बढ़ता है। इस घटना का स्पष्टीकरण मूल लेख में पाया जा सकता है।

यहाँ अनुसूची है $$$R_M$ । $$$S_M$ । $$$R _ {- M}$ और $$$S _ {- M}$ उल्टे एलएसबी वाले पिक्सल की संख्या के आधार पर, इसे आरएस आरेख कहा जाता है। एक्स अक्ष उल्टे एलएसबी के साथ पिक्सल का प्रतिशत है, वाई अक्ष मास्क एम और -एम के साथ नियमित और एकवचन समूहों की सापेक्ष संख्या है। $$$M = [0 ~ 1 ~ 1 ~ 0]$ ।



आरएस स्टेग्नालिसिस विधि का सार आरएस आरेख के चार घटता का मूल्यांकन करना और एक्सट्रपलेशन का उपयोग करके उनके चौराहे की गणना करना है। मान लें कि हमारे पास एक स्टेग्नकॉनटेनर है जिसमें अनजान लंबाई पी के संदेश के रूप में (पिक्सेल के प्रतिशत के रूप में) बेतरतीब ढंग से चयनित पिक्सल (यानी रैंडम एलएसबी का उपयोग करके) के निचले हिस्सों में एम्बेडेड है। आर और एस समूहों की संख्या के बारे में हमारी प्रारंभिक माप बिंदुओं के अनुरूप है $$$R_M (p / 2)$ । $$$S_M (p / 2)$ । $$$आर _ {- एम} (पी / 2)$ और $$$S _ {- M} (पी / 2)$ । हम संदेश की लगभग आधी लंबाई से अंक लेते हैं, क्योंकि संदेश एक यादृच्छिक बिट स्ट्रीम है और औसतन, जैसा कि पहले उल्लेख किया गया है, संदेश को एम्बेड करके केवल एक आधा पिक्सेल बदला जाएगा।

यदि हम छवि में सभी पिक्सेल के एलएसबी को उल्टा करते हैं और आर और एस समूहों की संख्या की गणना करते हैं, तो हमें चार अंक मिलते हैं $$$R_M (1-p / 2)$ । $$$S_M (1-p / 2)$ । $$$R _ {- M} (1-p / 2)$ और $$$S _ {- M} (1-p / 2)$ । चूंकि ये दो बिंदु एलएसबी के विशिष्ट यादृच्छिकरण पर निर्भर करते हैं, इसलिए हमें इस प्रक्रिया को कई बार दोहराना होगा और मूल्यांकन करना होगा $$$R_M (1/2)$ और $$$S_M (1/2)$ सांख्यिकीय नमूनों से।

हम सशर्त रूप से बिंदुओं के माध्यम से रेखाएँ खींच सकते हैं $$$आर _ {- एम} (पी / 2)$ । $$$R _ {- M} (1-p / 2)$ और $$$S _ {- M} (पी / 2)$ । $$$S _ {- M} (1-p / 2)$ ।

अंक $$$R_M (p / 2)$ । $$$R_M (1/2)$ । $$$R_M (1-p / 2)$ और $$$S_M (p / 2)$ । $$$S_M (1/2)$ । $$$S_M (1-p / 2)$ दो parabolas परिभाषित करें। प्रत्येक परवलय और इसी रेखा बाईं ओर प्रतिच्छेद करती है। दोनों चौराहों के एक्स-निर्देशांक का अंकगणितीय माध्य हमें अज्ञात संदेश लंबाई पी का अनुमान लगाने की अनुमति देता है।

मध्यबिंदु आरएम (1/2) और एसएम (1/2) के लंबे सांख्यिकीय अनुमान से बचने के लिए, कुछ और विचार किए जा सकते हैं:

1. वक्र चौराहा बिंदु $$$R_M$ और $$$R _ {- M}$ उसी x को वक्रों के लिए प्रतिच्छेदन बिंदु के रूप में समन्वित किया गया है $$$S_M$ और $$$S _ {- M}$ । यह अनिवार्य रूप से हमारी सांख्यिकीय परिकल्पना का अधिक कठोर संस्करण है। (ऊपर देखें)
2. आरएम और एसएम घटता m = 50%, या पर प्रतिच्छेद करते हैं $$$R_M (1/2) = S_M (1/2)$ ।

ये दो धारणाएं गुप्त संदेश पी की लंबाई के लिए एक सरल सूत्र प्रदान करती हैं। X अक्ष को स्केल करने के बाद, p / 2 0 हो जाता है और 1 - p / 2 1 हो जाता है, प्रतिच्छेदन बिंदु का x-निर्देशांक निम्नलिखित द्विघात समीकरण की जड़ है



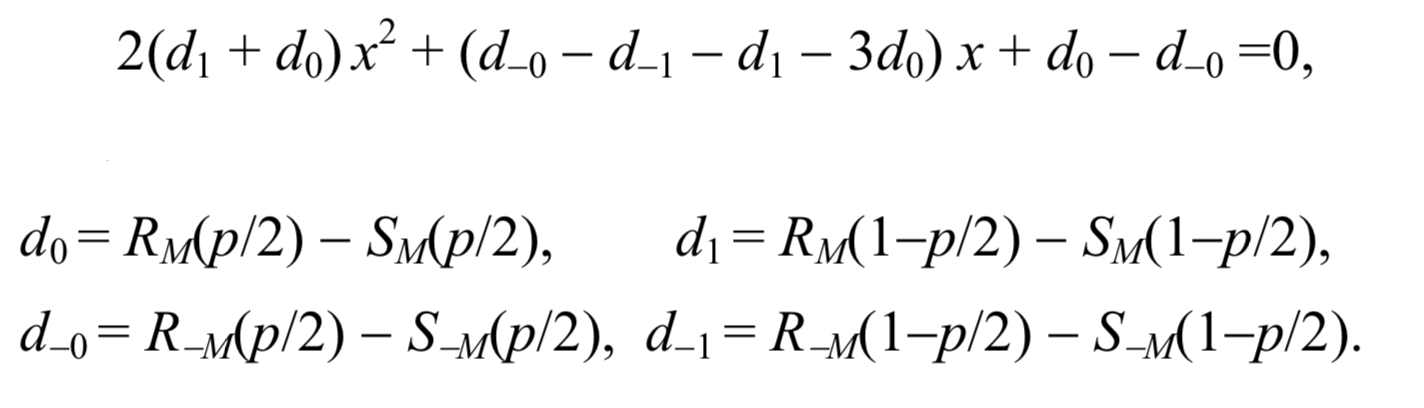
तब संदेश की लंबाई की गणना सूत्र द्वारा की जा सकती है:

$$

$$p = \ frac {x} {x- \ frac {1} {2}}$$

यहाँ हमारी बिल्ली दृश्य में प्रवेश करती है। (क्या उसे नाम देने का समय नहीं है?)

तो हमारे पास है:

• नियमित आरएम समूह (पी / 2): 23121 पीसी।
• एकल एसएम समूह (पी / 2): 14124 पीसी।
• इन्वर्टेड मास्क आरएम (पी / 2) के साथ नियमित समूह: 37191 पीसी।
• उल्टे मास्क एसएम (पी / 2) के साथ एकवचन समूह: 8440 पीसी।
• उल्टे एलएसबी आरएम (1-पी / 2) के साथ नियमित समूह: 20298 पीसी।
• उल्टे एलएसबी एसएम (1-पी / 2) के साथ एकवचन समूह: 16206 पीसी।
• एलएसबी के साथ और उल्टे मास्क आरएम (1-पी / 2) के साथ नियमित समूह: 40603 पीसी।
• एलएसबी के साथ और उल्टे मास्क एसएम (1-पी / 2) के साथ एकवचन समूह: 6947 पीसी।

(यदि आपके पास बहुत खाली समय है, तो आप उन्हें स्वयं गणना कर सकते हैं, लेकिन अब मैं सुझाव देता हूं कि आप मेरी गणना पर विश्वास करें)

एजेंडे पर, हमने एक नंगे गणित को छोड़ दिया है। फिर भी याद रखें कि द्विघात समीकरणों को कैसे हल करें?

$$

$$d_0 = 8997$$

$$

$$d _ {- 0} = $ 2875$$

$$

$$d_1 = 4092$$

$$

$$d _ {- 1} = 33656$$

उपरोक्त सभी सूत्र में प्रतिस्थापित करते हुए, हम एक द्विघात समीकरण प्राप्त करते हैं, जिसे हम स्कूल में पढ़ाए गए अनुसार हल करते हैं।

$$

$$26178x ^ 2-35988x - 19754 = 0$$

$$

$$D = (-35988) ^ 2 - 426178 * (- 19754) = $ 336361699$$

$$

$$x_1 = 1.7951 ~~~~~~~~ x_2 = -0.4204$$

एक छोटा मापांक लें, अर्थात $$$x_2$ । फिर बिल्ली में निर्मित संदेश के लिए अनुमानित अनुमान यह होगा:

$$

$$p = \ frac {-0.4204} {- 0.4204 - 0.5} = 0.4567$$

हां, इस विधि में एक बड़ा प्लस और एक बड़ा ऋण है। लाभ यह है कि विधि सामान्य एलएसबी स्टेग्नोग्राफ़ी और रैंडमएलएसबी स्टेग्नोग्राफ़ी दोनों के साथ काम करती है। एक ची-वर्ग इस तरह के अवसर का दावा नहीं कर सकता। विधि ने हमारी यादृच्छिक-दिखने वाली बिल्ली को सही पहचान लिया और 0.3256 पर संदेश की लंबाई का अनुमान लगाया, जो बहुत सटीक है।

इस पद्धति की बड़ी (बहुत बड़ी) त्रुटि में माइनस निहित है, जो क्रमिक एम्बेडिंग के साथ लंबे संदेश के साथ बढ़ता है। उदाहरण के लिए, 30% अधिभोग के साथ एक बिल्ली के लिए, विधि का मेरा कार्यान्वयन कुल क्षमता के तीन चैनलों के लिए अनुमानित औसत अनुमान देता है या कुल क्षमता का 46%, 95% से अधिक की अधिभोग के साथ - 0.8597। लेकिन एक खाली बिल्ली के लिए 0.0054 जितना। और यह एक सामान्य प्रवृत्ति है जो कार्यान्वयन से स्वतंत्र है। साधारण एलएसबी विधि के साथ सबसे सटीक परिणाम एक अंतर्निहित संदेश लंबाई 10% + - 5% देते हैं।

प्लस या माइनस

पकड़े न जाने के लिए, किसी को अप्रत्याशित होना चाहिए और ing 1 कोडिंग का उपयोग करना चाहिए। रंग बाइट में कम से कम महत्वपूर्ण बिट को बदलने के बजाय, हम या तो एक-एक करके पूरे बाइट को बढ़ाएंगे या घटाएंगे। केवल दो अपवाद हैं:

• हम शून्य को कम नहीं कर सकते, इसलिए हम इसे बढ़ाएंगे,
  
• हम 255 भी नहीं बढ़ा सकते, इसलिए हम हमेशा इस मूल्य को कम करेंगे।
  

अन्य सभी बाइट मूल्यों के लिए, हम पूरी तरह से बेतरतीब ढंग से या तो एक की वृद्धि या एक कमी का चयन करते हैं। इस हेरफेर के शीर्ष पर, एलएसबी पहले की तरह बदल जाएगा। अधिक विश्वसनीयता के लिए, संदेश रिकॉर्ड करने के लिए यादृच्छिक बाइट्स लेना बेहतर है।

यहाँ हमारी दोस्त बिल्ली है:



बाह्य रूप से, परिचय अनिवार्य रूप से ठीक उसी कारण से होता है, जिस कारण (0, 0, 0) और (1, 1, 1) के बीच अंतर दिखाई नहीं देता था।



एलएसबी स्लाइस यादृच्छिक स्थानों में रिकॉर्डिंग के कारण बस शोर रहता है।



ची-वर्ग अभी भी अंधा है, और आरएस विधि 0.0036 का मोटा अनुमान लगाती है।

बहुत खुश नहीं होने के लिए, इस लेख को यहां पढ़ें।

सबसे चौकस लोग पूछ सकते हैं कि कैसे हम एक संदेश प्राप्त कर सकते हैं यदि पूरे बाइट्स को बेतरतीब ढंग से बदल दिया जाता है, और हमारे पास PRNG सेट करने के लिए पासवर्ड नहीं है (रैंडमएलएसबी और ± 1 एन्कोडिंग के साथ काम करने के लिए जनरेटर उर्फ ​​पासवर्ड की स्थिति के लिए अलग-अलग बीजों का उपयोग करना बेहतर है)। इसका उत्तर यथासंभव सरल है। हमें वह संदेश मिलता है जिस तरह से हमने। 1 एन्कोडिंग के बिना किया था। हम इसके उपयोग के बारे में भी नहीं जानते होंगे। मैं दोहराता हूं, हम इस चाल का उपयोग केवल स्वचालित पहचान उपकरणों को बायपास करने के लिए करते हैं । किसी संदेश को एम्बेड / पुनः प्राप्त करते समय, हम केवल उसके LSB के साथ काम करते हैं और इससे अधिक कुछ नहीं। हालांकि, जब पता लगाते हैं, तो हमें सांख्यिकीय अनुमानों को बनाने के लिए कार्यान्वयन संदर्भ, छवि के सभी बाइट्स को ध्यान में रखना होगा। यह ठीक is 1 कोडिंग की पूरी सफलता है।

एक निष्कर्ष के बजाय

एलएसबी स्टेग्नोग्राफ़ी के खिलाफ आँकड़ों का उपयोग करने का एक और बहुत अच्छा प्रयास नमूना जोड़े नामक एक विधि में किया गया था। आप इसे यहाँ पा सकते हैं । यहां उनकी उपस्थिति लेख को बहुत अधिक अकादमिक बना देगी, इसलिए मैं इसे एक्स्ट्रा करिकुलर रीडिंग के लिए दिलचस्पी लेता हूं। लेकिन दर्शकों के सवालों का अनुमान लगाते हुए, मैं तुरंत जवाब दूंगा: नहीं, वह cod 1 कोडिंग नहीं पकड़ता।

और बेशक मशीन लर्निंग। एमएल पर आधारित आधुनिक तरीके बहुत अच्छे परिणाम देते हैं। आप इसके बारे में यहाँ और यहाँ पढ़ सकते हैं।

इस लेख के आधार पर, एक छोटा उपकरण लिखा गया था (अब के लिए)। यह डेटा उत्पन्न कर सकता है, चैनलों पर अलग से एक दृश्य हमले कर सकता है, आरएस की गणना कर सकता है-, एसपीए-आकलन और ची-स्क्वायर के परिणामों की कल्पना कर सकता है। और वह वहाँ रुकने वाली नहीं है।

संक्षेप में, मैं कुछ सुझाव देना चाहता हूं:

• संदेश को यादृच्छिक बाइट्स में एम्बेड करें।
• जितना हो सके एम्बेडेड जानकारी की मात्रा कम करें (चाचा हैमिंग याद रखें)।
• Use 1 कोडिंग का उपयोग करें।
• शोर LSB के साथ तस्वीरें चुनें।
• रेमलडैप का यूपीडी : ऐसी छवियों का उपयोग करें जो कहीं भी दिखाई न दें।
• अच्छा बनो!

मुझे आपके सुझाव, परिवर्धन, सुधार और अन्य प्रतिक्रिया देखकर खुशी होगी!

PS मैं परामर्श और प्रेरक किक के लिए PavelMSTU के लिए विशेष धन्यवाद व्यक्त करना चाहता हूं।