🧝🏽 ♊️ 👩‍🚀 आलसी कम्प्यूटिंग पेड़ों की डिस्क कैशिंग ♉️ 🚩 👁️

आलसी कंप्यूटिंग की अवधारणा शायद ही विस्तार से बात करने लायक है। एक ही चीज़ को कम बार करने का विचार, खासकर अगर यह लंबा और कठिन है, तो दुनिया जितनी पुरानी है। क्योंकि तुरंत टू द पॉइंट।

इस पाठ के लेखक के अनुसार, एक सामान्य साहित्यकार को चाहिए:

प्रोग्राम कॉल के बीच गणना सहेजें।
गणना पेड़ में परिवर्तन को ट्रैक करें।
मध्यम रूप से पारदर्शी सिंटैक्स लें।

आलसी वृक्ष

संकल्पना

क्रम में:

कार्यक्रम कॉल के बीच गणना सहेजें:
वास्तव में, यदि हम एक ही स्क्रिप्ट को दिन में कई बार दसियों-सैकड़ों बार कहते हैं, तो हमें उसी समय को पुन: गणना क्यों करनी चाहिए, जब स्क्रिप्ट को किसी फ़ाइल में परिणाम वस्तु को संग्रहीत करना संभव हो। डिस्क से किसी ऑब्जेक्ट को खींचना बेहतर है, लेकिन ... हमें इसकी प्रासंगिकता के बारे में सुनिश्चित होना चाहिए। अचानक स्क्रिप्ट फिर से लिखी जाती है और सहेजा गया ऑब्जेक्ट पुराना हो जाता है। इसके आधार पर, हम किसी फ़ाइल के अस्तित्व पर वस्तु को लोड नहीं कर सकते। दूसरा बिंदु इस प्रकार है।
गणना पेड़ में परिवर्तन ट्रैक:
ऑब्जेक्ट को अपडेट करने की आवश्यकता को डेटा के आधार पर गणना की जानी चाहिए ताकि फ़ंक्शन इसे उत्पन्न कर सके। इसलिए हम सुनिश्चित करेंगे कि लोड की गई वस्तु वैध है। वास्तव में, एक शुद्ध कार्य के लिए, वापसी मूल्य केवल तर्कों पर निर्भर करता है। इसका मतलब यह है कि जब हम शुद्ध कार्यों के परिणामों को कैश करते हैं और तर्कों के परिवर्तन की निगरानी करते हैं, तो हम कैश की प्रासंगिकता के बारे में शांत हो सकते हैं। उसी समय, यदि गणना की गई वस्तु दूसरे कैश्ड (आलसी) ऑब्जेक्ट पर निर्भर करती है, जो बदले में दूसरे पर निर्भर करती है, तो आपको इन ऑब्जेक्ट्स में बदलावों को सही ढंग से काम करने की आवश्यकता है, जो समय-समय पर चेन नोड्स को अपडेट करते हैं जो अब प्रासंगिक नहीं हैं। दूसरी ओर, यह ध्यान रखना अच्छा होगा कि हमें हमेशा पूरी गणना श्रृंखला के डेटा को लोड करने की आवश्यकता नहीं है। अक्सर, केवल अंतिम परिणाम ऑब्जेक्ट को लोड करना पर्याप्त होता है।
मध्यम रूप से पारदर्शी सिंटैक्स लें:
यह बात स्पष्ट है। यदि स्क्रिप्ट को आलसी गणनाओं को फिर से लिखने के लिए पूरे कोड को बदलना आवश्यक है, तो यह एक तथाकथित समाधान है। बदलाव न्यूनतम किया जाना चाहिए।

रीज़निंग की इस पंक्ति के कारण तकनीकी समाधान हुआ, जिसे पाइलटॉन द्वारा विकसित किया गया, जो कि इवाल्केच लाइब्रेरी (लेख के अंत में लिंक) है।

सिंटैक्स समाधान और काम का तंत्र

सरल उदाहरण है

import evalcache import hashlib import shelve lazy = evalcache.Lazy(cache = shelve.open(".cache"), algo = hashlib.sha256) @lazy def summ(a,b,c): return a + b + c @lazy def sqr(a): return a * a a = 1 b = sqr(2) c = lazy(3) lazyresult = summ(a, b, c) result = lazyresult.unlazy() print(lazyresult) #f8a871cd8c85850f6bf2ec96b223de2d302dd7f38c749867c2851deb0b24315c print(result) #8

यह कैसे काम करता है?

पहली चीज जो आपकी आंख को पकड़ती है वह आलसी डेकोरेटर का निर्माण है। पायथन पायथन के लिए इस तरह के एक वाक्यविन्यास समाधान काफी मानक है। आलसी डेकोरेटर को कैशे ऑब्जेक्ट पास किया जाता है जिसमें लेनिकेटर गणना के परिणामों को संग्रहीत करेगा। तानाशाह की तरह इंटरफ़ेस की आवश्यकताओं को कैश प्रकार पर आरोपित किया जाता है। दूसरे शब्दों में, हम हर चीज को कैश कर सकते हैं जो उसी प्रकार के इंटरफ़ेस को लागू करता है जैसे कि तानाशाही। ऊपर के उदाहरण में प्रदर्शित करने के लिए, हमने शेल्व लाइब्रेरी से शब्दकोश का उपयोग किया।

डेकोरेटर को एक हैश प्रोटोकॉल भी भेजा जाता है, जिसका उपयोग वह वस्तुओं की हैश कीज़ और कुछ अतिरिक्त विकल्पों (लिखने की अनुमति, रीड अनुमति, डिबग आउटपुट) के निर्माण के लिए करेगा, जिसे दस्तावेज़ या कोड में पाया जा सकता है।

डेकोरेटर को अन्य प्रकार के कार्यों और वस्तुओं दोनों पर लागू किया जा सकता है। इस समय, एक आलसी वस्तु उनके आधार पर एक हैश कुंजी के साथ बनाई गई है जो प्रतिनिधित्व के आधार पर गणना की जाती है (या इस प्रकार के फ़ंक्शन के लिए विशेष रूप से परिभाषित हैश फ़ंक्शन का उपयोग करके)।

पुस्तकालय की एक प्रमुख विशेषता यह है कि एक आलसी वस्तु अन्य आलसी वस्तुओं को फैला सकती है, और माता-पिता (या माता-पिता) के हैश को वंशज की हैश कुंजी में मिलाया जाएगा। आलसी वस्तुओं के लिए, ऑब्जेक्ट्स के कॉल ( __call__ ) का उपयोग करके और ऑपरेटरों का उपयोग करके, एक विशेषता लेने के संचालन का उपयोग करने की अनुमति है।

स्क्रिप्ट से गुजरते समय, वास्तव में, कोई गणना नहीं की जाती है। बी के लिए, वर्ग की गणना नहीं की जाती है, और lazyresult के लिए, तर्कों के योग पर विचार नहीं किया जाता है। इसके बजाय, संचालन का एक पेड़ बनाया गया है और आलसी वस्तुओं की हैश कीज़ की गणना की जाती है।

वास्तविक गणना (यदि परिणाम पहले कैश में नहीं डाला गया था) केवल लाइन में किया जाएगा: result = lazyresult.unlazy()

यदि ऑब्जेक्ट पहले गणना की गई थी, तो इसे फ़ाइल से लोड किया जाएगा।
आप बिल्ड ट्री की कल्पना कर सकते हैं:

वृक्ष दृश्य का निर्माण

 evalcache.print_tree(lazyresult) ... generic: <function summ at 0x7f1cfc0d5048> args: 1 generic: <function sqr at 0x7f1cf9af29d8> args: 2 ------- 3 -------

चूँकि इन वस्तुओं को उत्पन्न करने वाले तर्कों के बारे में आंकड़ों के आधार पर वस्तुओं का हैश बनाया जाता है, जब तर्क में परिवर्तन होता है, तो वस्तु का हैश बदलता है और इसके आधार पर पूरी श्रृंखला का हैश होता है। इससे आप समय पर अपडेट करके कैशे डेटा को अपडेट रख सकते हैं।

आलसी वस्तुएँ एक वृक्ष में पंक्तिबद्ध हो जाती हैं। यदि हम वस्तुओं में से किसी एक पर अस्वाभाविक संचालन करते हैं, तो ठीक उसी तरह जैसे कि कई वस्तुओं को लोड किया जाएगा और एक वैध परिणाम प्राप्त करने के लिए आवश्यक गिना जाएगा। आदर्श रूप से, आवश्यक वस्तु बस लोड होगी। इस स्थिति में, एल्गोरिथ्म ऑब्जेक्ट को मेमोरी में नहीं खींचेगा।

कार्रवाई में

ऊपर एक सरल उदाहरण था जो वाक्य रचना को दिखाता है लेकिन दृष्टिकोण की कम्प्यूटेशनल शक्ति को प्रदर्शित नहीं करता है।
यहाँ एक उदाहरण है वास्तविक जीवन के थोड़ा करीब (सहानुभूति द्वारा प्रयुक्त)।

उदाहरण सिम्पी और सुन्न का उपयोग कर

 #!/usr/bin/python3.5 from sympy import * import numpy as np import math import evalcache lazy = evalcache.Lazy(evalcache.DirCache(".evalcache"), diag = True) pj1, psi, y0, gamma, gr= symbols("pj1 psi y0 gamma gr") ###################### Construct sympy expression ##################### F = 2500 xright = 625 re = 625 y0 = 1650 gr = 2*math.pi / 360 #gamma = pi / 2 xj1q = xright + re * (1 - cos(psi)) yj1q = (xright + re) * tan(psi) - re * sin(psi) #+ y0 pj1 = sqrt(xj1q**2 + yj1q**2) pj2 = pj1 + y0 * sin(psi) zj2 = (pj2**2)/4/F asqrt = sqrt(pj2**2 + 4*F**2) xp2 = 2*F / asqrt yp2 = pj2 / asqrt xp3 = yp2 yp3 = -xp2 xmpsi = 1295 gmpsi = 106 * gr aepsi = 600 bepsi = 125 b = 0.5*(1-cos(pi * gamma / gmpsi)) p1 = ( (gamma * xmpsi / gmpsi * xp2) * (1-b) + (aepsi * xp2 * sin(gamma) + bepsi * yp2 * (1-cos(gamma)))*b + pj1 ) ####################################################################### #First lazy node. Simplify is long operation. #Sympy has very good representations for expressions print("Expression:", repr(p1)) print() p1 = lazy(simplify)(p1) ######################################################################################### ## Really don't need to lazify fast operations Na = 200 angles = [t * 2 * math.pi / 360 / Na * 106 for t in range(0,Na+1)] N = int(200) a = (np.arange(0,N+1) - N/2) * 90/360*2*math.pi/N ######################################################################################### @lazy def genarray(angles, a, p1): points = [] for i in range(0, len(angles)): ex = p1.subs(gamma, angles[i]) func = lambdify(psi, ex, 'numpy') # returns a numpy-ready function rads = func(a) xs = rads*np.cos(a) ys = rads*np.sin(a) arr = np.column_stack((xs,ys,[i*2]*len(xs))) points.append(arr) return points #Second lazy node. arr = genarray(angles, a, p1).unlazy() print("\nResult list:", arr.__class__, len(arr))

प्रतीकात्मक अभिव्यक्तियों को सरल बनाने के लिए संचालन बेहद महंगा है और शाब्दिक रूप से ऋण देने के लिए कहते हैं। एक बड़े सरणी के आगे के निर्माण में और भी अधिक समय लगता है, लेकिन ऋणशोधन के लिए धन्यवाद, परिणाम कैश से खींच लिए जाएंगे। कृपया ध्यान दें कि यदि स्क्रिप्ट के शीर्ष पर कुछ गुणांक बदल दिए जाते हैं जहां सहानुभूति की अभिव्यक्ति उत्पन्न होती है, तो परिणामों को पुनर्गणित किया जाएगा क्योंकि आलसी वस्तु का हैश कुंजी बदल जाएगा (शांत __repr__ स्टेटमेंट के लिए धन्यवाद)।

अक्सर, एक स्थिति तब होती है जब एक शोधकर्ता लंबे समय से उत्पन्न वस्तु पर कम्प्यूटेशनल प्रयोगों का आयोजन करता है। यह पीढ़ी और ऑब्जेक्ट के उपयोग को अलग करने के लिए कई लिपियों का उपयोग कर सकता है, जो डेटा को असंगत रूप से अपडेट करने में समस्या पैदा कर सकता है। प्रस्तावित दृष्टिकोण इस मामले को सुविधाजनक बना सकता है।

यह सब क्या है?

evalcache zencad परियोजना का हिस्सा है। यह एक छोटी स्क्रिप्ट कैडिक है, जो ओपनकैड के समान विचारों को प्रेरित और शोषण करती है। जाली उन्मुख ओपेकैड के विपरीत, ओपेकनकेड कोर पर चलने वाला ज़ेंकाड वस्तुओं के संक्षिप्त प्रतिनिधित्व का उपयोग करता है, और स्क्रिप्ट अजगर में लिखी जाती हैं।

ज्यामितीय संचालन अक्सर लंबे समय तक किया जाता है। कैड स्क्रिप्टिंग सिस्टम का नुकसान यह है कि हर बार जब आप स्क्रिप्ट चलाते हैं, तो उत्पाद पूरी तरह से फिर से जुड़ जाता है। इसके अलावा, मॉडल की वृद्धि और जटिलता के साथ, ओवरहेड लागत रैखिक रूप से नहीं बढ़ती है। यह इस तथ्य की ओर जाता है कि आप केवल बहुत छोटे मॉडल के साथ आराम से काम कर सकते हैं।

इस समस्या का हल निकालने का काम था। ज़ेंकड में, सभी ऑपरेशनों को आलसी घोषित किया जाता है।

उदाहरण:

मॉडल बिल्डिंग का उदाहरण

 #!/usr/bin/python3 #coding: utf-8 from zencad import * xgate = 14.65 ygate = 11.6 zgate = 11 t = (xgate - 11.7) / 2 ear_r = 8.6/2 ear_w = 7.8 - ear_r ear_z = 3 hx_h = 2.0 bx = xgate + ear_w by = 2 bz = ear_z+1 gate = ( box(xgate, ygate, t).up(zgate - t) + box(t, ygate, zgate) + box(t, ygate, zgate).right(xgate - t) ) gate = gate.fillet(1, [5, 23,29, 76]) gate = gate.left(xgate/2) ear = (box(ear_w, ear_r * 2, ear_z) + cylinder(r = ear_r, h = ear_z).forw(ear_r).right(ear_w)).right(xgate/2 - t) hx = linear_extrude( ngon(r = 2.5, n = 6).rotateZ(deg(90)).forw(ear_r), hx_h ).up(ear_z - hx_h).right(xgate/2 -t + ear_w) m = ( gate + ear + ear.mirrorYZ() - hx - hx.mirrorYZ() - box(xgate-2*t, ygate, zgate, center = True).forw(ygate/2) - box(bx, by, bz, center = True).forw(ear_r).up(bz/2) - cylinder(r = 2/2, h = 100, center = True).right(xgate/2-t+ear_w).forw(ear_r) - cylinder(r = 2/2, h = 100, center = True).left(xgate/2-t+ear_w).forw(ear_r) ) display(m) show()

यह स्क्रिप्ट निम्नलिखित मॉडल उत्पन्न करता है:

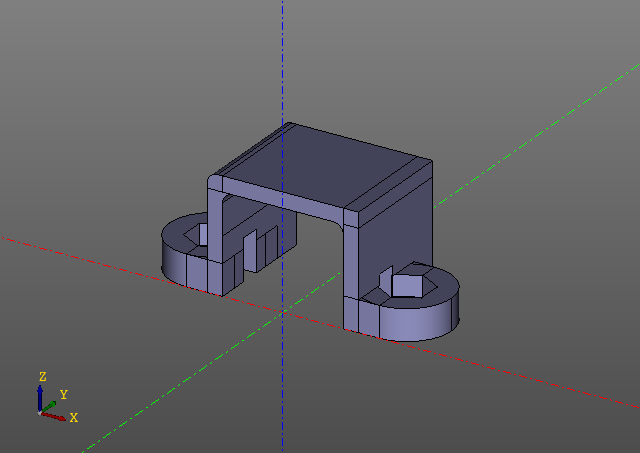
ध्यान दें कि स्क्रिप्ट में कोई evalcache कॉल नहीं हैं। चाल यह है कि लेनडिकेशन ज़ेंकाड लाइब्रेरी में ही अंतर्निहित है और यह पहली नज़र में भी दिखाई नहीं देता है, हालांकि यहां सभी काम आलसी वस्तुओं के साथ काम कर रहे हैं, और प्रत्यक्ष गणना केवल 'डिस्प्ले' फ़ंक्शन में की जाती है। बेशक, यदि कुछ मॉडल पैरामीटर को बदल दिया जाता है, तो मॉडल उस स्थान से फिर से जुड़ जाएगा जहां पहली हैश कुंजी बदल गई है।

भारी कम्प्यूटिंग मॉडल

यहाँ एक और उदाहरण है। इस बार हम खुद को तस्वीरों तक सीमित रखेंगे:

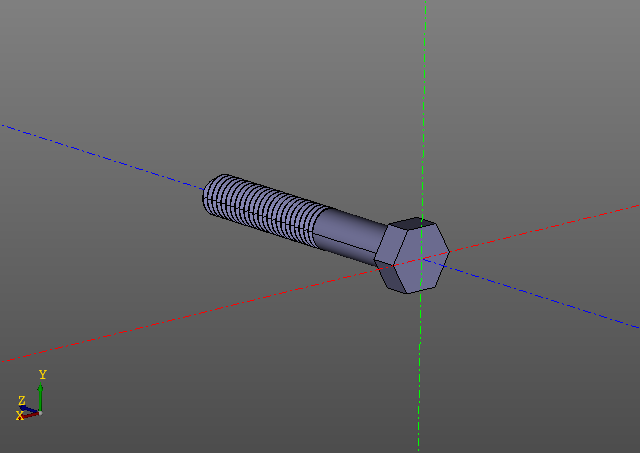
एक थ्रेडेड सतह की गणना एक आसान काम नहीं है। मेरे कंप्यूटर पर, ऐसा बोल्ट दस सेकंड के आदेश पर बनाया गया है ... थ्रेड के साथ एक मॉडल का संपादन कैशिंग का उपयोग करके बहुत अधिक सुखद है।

और अब यह एक चमत्कार है:

थ्रेडेड सतहों को पार करना एक जटिल कम्प्यूटेशनल कार्य है। व्यावहारिक मूल्य, हालांकि, गणित की जाँच के अलावा और कोई नहीं। गणना में डेढ़ मिनट का समय लगता है। लेन देन के लिए एक योग्य लक्ष्य।

समस्याओं

कैश उद्देश्य के अनुसार काम नहीं कर सकता है।
कैश त्रुटियों को झूठे सकारात्मक और झूठे नकारात्मक में विभाजित किया जा सकता है।

गलत नकारात्मक त्रुटियाँ

गलत नकारात्मक त्रुटियां ऐसी परिस्थितियां हैं जहां गणना का परिणाम कैश में है, लेकिन सिस्टम ने इसे नहीं पाया।
ऐसा तब होता है जब किसी कारण से evalcache द्वारा उपयोग किया गया हैश कुंजी एल्गोरिथ्म पुनर्गणना के लिए एक अलग कुंजी का उत्पादन करता है। यदि कैश प्रकार के ऑब्जेक्ट के लिए हैश फ़ंक्शन ओवरराइड नहीं किया गया है, तो evalcache कुंजी का निर्माण करने __repr__ ऑब्जेक्ट के __repr__ का उपयोग करता है।
एक त्रुटि तब होती है, उदाहरण के लिए, यदि लीज की जा रही कक्षा मानक object.__repr__ ओवरराइड नहीं object.__repr__ , जो शुरू से शुरू होने तक बदलती रहती है। या, यदि ओवरराइड __repr__ , किसी तरह बदलते डेटा की गणना के लिए महत्वहीन है (जैसे कि ऑब्जेक्ट या टाइमस्टैम्प का पता)।

खराब:

 class A: def __init__(self): self.i = 3 A_lazy = lazy(A) A_lazy().unlazy() #        -  __repr__.

अच्छा:

 class A: def __init__(self): self.i = 3 def __repr__(self): return "A({})".format(self.i) A_lazy = lazy(A) A_lazy().unlazy() #     .

गलत नकारात्मक त्रुटियां इस तथ्य की ओर ले जाती हैं कि लेन देन काम नहीं करता है। प्रत्येक नए स्क्रिप्ट निष्पादन पर ऑब्जेक्ट को फिर से लिखा जाएगा।

झूठी सकारात्मक त्रुटियों

यह एक और अधिक प्रकार की त्रुटि है, क्योंकि यह गणना की अंतिम वस्तु में त्रुटियों की ओर जाता है:
यह दो कारणों से हो सकता है।

अविश्वसनीय:
कैश में हैश की टक्कर हुई। Sha256 एल्गोरिथ्म के लिए 1157920892373161954235709850086879078532699846656405640394584847913129639936 संभावित कुंजियों का एक स्थान होने की संभावना है, एक टकराव की संभावना नगण्य है।
संभावित:
एक वस्तु का एक प्रतिनिधित्व (या एक अधिकता हैश फ़ंक्शन) पूरी तरह से इसका वर्णन नहीं करता है, या किसी अन्य प्रकार की वस्तु के प्रतिनिधित्व के साथ मेल खाता है।

 class A: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) class B: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) A_lazy = lazy(A) B_lazy = lazy(B) a = A_lazy().unlazy() b = B_lazy().unlazy() #.     B,        A.

दोनों समस्याएं एक असंगत __repr__ ऑब्जेक्ट से संबंधित हैं। यदि किसी कारण से __repr__ ऑब्जेक्ट प्रकार को अधिलेखित करना असंभव है, तो लाइब्रेरी आपको उपयोगकर्ता प्रकार के लिए एक विशेष हैश फ़ंक्शन सेट करने की अनुमति देती है।

एनालॉग्स के बारे में

ऐसे कई लेन-देन पुस्तकालय हैं जो मूल रूप से स्क्रिप्ट कॉल के अनुसार एक बार से अधिक गणना को चलाने के लिए पर्याप्त मानते हैं।

कई डिस्क कैशिंग लाइब्रेरी हैं, जो आपके अनुरोध पर, आपके लिए आवश्यक कुंजी के साथ एक ऑब्जेक्ट को बचाएगा।

लेकिन मैं अभी भी पुस्तकालयों को नहीं खोज सका जो निष्पादन पेड़ पर कैशिंग परिणामों की अनुमति देगा। यदि कोई हो, तो कृपया, असुरक्षित।

संदर्भ:

गिथब परियोजना
पिपी परियोजना

आलसी कम्प्यूटिंग पेड़ों की डिस्क कैशिंग