सबसे तेज़ जंगली पश्चिम फ़्लोटिंग पॉइंट नंबर

एक "रीडर" को लागू करने की प्रक्रिया में, गणना की सटीकता में वृद्धि के साथ एक समस्या उत्पन्न हुई। गणना एल्गोरिथ्म ने मानक फ़्लोटिंग-पॉइंट संख्याओं पर तेज़ी से काम किया, लेकिन जब सटीक गणना के लिए पुस्तकालय जुड़े थे, तो सब कुछ बेतहाशा धीमा होने लगा। इस लेख में, हम मल्टीकोम्पोनेंट दृष्टिकोण का उपयोग करके फ्लोटिंग-पॉइंट संख्या का विस्तार करने के लिए एल्गोरिदम पर विचार करेंगे, जिसके कारण हम त्वरण प्राप्त करने में कामयाब रहे, क्योंकि फ्लोट अंकगणित एक सीपी चिप पर लागू होता है। यह दृष्टिकोण संख्यात्मक व्युत्पन्न, मैट्रिक्स उलटा, बहुभुज ट्रिमिंग या अन्य ज्यामितीय समस्याओं की अधिक सटीक गणना के लिए उपयोगी होगा। इसलिए वीडियो कार्ड पर 64 बिट फ्लोट का अनुकरण करना संभव है जो उनका समर्थन नहीं करते हैं।

परिचय

जैसा कि निकुलास Wirth ने हमें 0 और 1 नंबर रखने के लिए वसीयत की, इसलिए हम उन्हें उन में संग्रहीत करते हैं। और क्या यह है कि मनुष्य दशमलव प्रणाली में रहते हैं, और प्रतीत होता है कि सामान्य संख्या 0.1 और 0.3 एक परिमित अंश द्वारा द्विआधारी प्रणाली में प्रतिनिधित्व करने योग्य नहीं हैं? जब हम उन पर गणना करते हैं तो हमें एक सांस्कृतिक झटका लगता है। बेशक, दशमलव प्रणाली के आधार पर प्रोसेसर के लिए पुस्तकालय बनाने का प्रयास किया जा रहा है और IEEE में भी मानकीकृत प्रारूप हैं।

लेकिन अभी के लिए, हम हर जगह बाइनरी स्टोरेज को ध्यान में रखते हैं और पुस्तकालयों के साथ सभी धन गणनाओं को सटीक गणना के लिए करते हैं, जैसे कि बिग्म्बर, जिससे प्रदर्शन का नुकसान होता है। मार्केटर्स कहते हैं कि एसाइक क्रिप्टो मानते हैं, और प्रोसेसर में इस दशमलव अंकगणित के लिए बहुत कम जगह है। इसलिए, जब एक संख्या एक अनियंत्रित संख्या के रूप में संग्रहीत की जाती है, तो एक बहुपद दृष्टिकोण, एक सुविधाजनक चाल है और सैद्धांतिक सूचना विज्ञान के क्षेत्र में एक सक्रिय रूप से विकासशील क्षेत्र है। हालाँकि डेकर अभी भी सटीकता के नुकसान के बिना, सही ढंग से गुणा करना सीख गया है, 1971 में, रेडी-टू-यूज़ लाइब्रेरी बहुत बाद में (एमपीएफआर, क्यूडी) और सभी भाषाओं में नहीं दिखाई दी, जाहिर है चूंकि सभी ने IEEE मानकों का समर्थन नहीं किया है, लेकिन बाद में भी गणना की त्रुटि के कठोर प्रमाण, उदाहरण के लिए 2017 में डबल-शब्द अंकगणित के लिए।

डबल-शब्द अंकगणित

क्या कहना है? दाढ़ी वाले समय में, जब फ़्लोटिंग संख्याओं के लिए कोई मानक नहीं थे, तो गोलाई के कार्यान्वयन के साथ समस्याओं से बचने के लिए, मोलर के साथ आया, और बाद में नुथ ने साबित किया कि त्रुटि-मुक्त योग है। इस तरह से चल रहा है

function quickTwoSum(a, b) { let s = a + b; let z = s - a; let e = b - z; return [s, e]; } 

इस एल्गोरिथ्म में, यह मान लिया गया था कि यदि $$$| ए | > | b |$ , तो उनकी सटीक राशि को दो संख्याओं के योग के रूप में दर्शाया जा सकता है $$$s + ई$ और आप उन्हें बाद की गणना के लिए जोड़े में रख सकते हैं, और एक नकारात्मक संख्या के साथ घटाव घटाया जाता है।



इसके बाद, डेकर ने दिखाया कि यदि फ़्लोटिंग-पॉइंट नंबरों का उपयोग किया जाता है जो निकटतम सम संख्या (राउंड-टू-नज़दीकी संबंधों के लिए भी राउंडिंग का उपयोग करते हैं, जो आम तौर पर एक सही प्रक्रिया है जो लंबी गणना और आईईईई मानक की प्रक्रिया में बड़ी त्रुटियों को जन्म नहीं देती है), फिर एक त्रुटि-मुक्त गुणन एल्गोरिथम है।

 function twoMult(a, b) { let A = split(a); let B = split(b); let r1 = a * b; let t1 = -r1 + A[0] * B[0]; let t2 = t1 + A[0] * B[1]; let t3 = t2 + A[1] * B[0]; return [r1, t3 + A[1] * B[1]]; } 

जहाँ विभाजन () एक संख्या को विभाजित करने के लिए श्री वेल्टकैंप के एल्गोरिथ्म है

 let splitter = Math.pow(2, 27) + 1; function split(a) { let t = splitter * a; let d = a - t; let xh = t + d; let xl = a - xh; return [xh, xl]; } 

निरंतर का उपयोग करना $$$C = 2 ^ s + 1$ जो मंटिसा के आधे से अधिक लंबाई के बराबर होता है, जो गुणा की प्रक्रिया में संख्याओं के अतिप्रवाह की ओर नहीं जाता है और मंटिसा को दो हिस्सों में विभाजित करता है। उदाहरण के लिए, एक शब्द की लंबाई 64-बिट के साथ, मंटिसा की लंबाई 53 और फिर s = 27 है।



इस तरह, डेकर ने दोहरे शब्द अंकगणित में कंप्यूटिंग के लिए आवश्यक लगभग पूरा सेट प्रदान किया। चूंकि वहाँ यह भी संकेत दिया गया था कि दो डबल-वर्ड संख्याओं को कैसे गुणा, विभाजित और वर्ग करें।

दो दोहरे शब्दों के योग के लिए उनका क्विकवॉसम एल्गोरिथम "इनलाइन" था, और चेक का उपयोग किया गया था $$$| ए | > | b |$ । आधुनिक प्रोसेसर पर, जैसा कि [4] में वर्णित है, एल्गोरिथ्म की शाखाओं की तुलना में संख्याओं के साथ अतिरिक्त संचालन का उपयोग करना सस्ता है। इसलिए, दो एकल-शब्द संख्याओं को जोड़ने के लिए अब निम्न एल्गोरिथम अधिक उपयुक्त है

 function twoSum(a, b) { let s = a + b; let a1 = s - b; let b1 = s - a1; let da = a - a1; let db = b - b1; return [s, da + db]; } 

और इसलिए यह दोहरे शब्द संख्याओं का योग और गुणन है।

 function add22(X, Y) { let S = twoSum(X[0], Y[0]); let E = twoSum(X[1], Y[1]); let c = S[1] + E[0]; let V = quickTwoSum(S[0], c); let w = V[1] + E[1]; return quickTwoSum(V[0], w); } function mul22(X, Y) { let S = twoMult(X[0], Y[0]); S[1] += X[0] * Y[1] + X[1] * Y[0]; return quickTwoSum(S[0], S[1]); } 

सामान्यतया, डबल-शब्द अंकगणित, सैद्धांतिक त्रुटि सीमाओं और व्यावहारिक कार्यान्वयन के लिए एल्गोरिदम की सबसे पूर्ण और सटीक सूची 2017 से लिंक [3] में वर्णित है। इसलिए, यदि दिलचस्पी है, तो मैं सीधे वहां जाने की सलाह देता हूं। सामान्य तौर पर, चौगुनी-शब्द के लिए एक एल्गोरिथ्म [6] में दिया जाता है, और [5] में मनमाने ढंग से लंबाई के एक बहुपद के विस्तार के लिए। केवल वहां, प्रत्येक ऑपरेशन के बाद, रेनोवेशन प्रक्रिया का उपयोग किया जाता है, जो हमेशा छोटे आकार के लिए इष्टतम नहीं होता है, और क्यूडी में गणना की सटीकता को सख्ती से परिभाषित नहीं किया जाता है। सामान्य तौर पर, यह निश्चित रूप से इन तरीकों की प्रयोज्यता की सीमाओं के बारे में सोचने योग्य है।

डरावनी कहानियाँ जावास्क्रिप्ट-ए। दशमलव की तुलना। Js बनाम bignumber.js बनाम big.js.

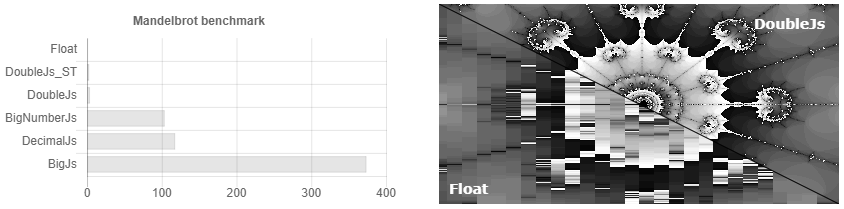
ऐसा हुआ कि js में सटीक गणना के लिए लगभग सभी पुस्तकालय एक व्यक्ति द्वारा लिखे गए थे। पसंद का भ्रम पैदा किया जाता है, हालांकि वे लगभग सभी समान हैं। इसके अलावा, प्रलेखन स्पष्ट रूप से इंगित नहीं करता है कि यदि आप प्रत्येक गुणन / विभाजन ऑपरेशन के बाद संख्याओं को गोल नहीं करते हैं, तो आपकी संख्या का आकार हर समय दोगुना हो जाएगा, और एल्गोरिथ्म की जटिलता x3500 में एक आसान में बढ़ सकती है। उदाहरण के लिए, उनके गणना समय की तुलना इस तरह दिख सकती है यदि आपने संख्याओं को गोल नहीं किया है।



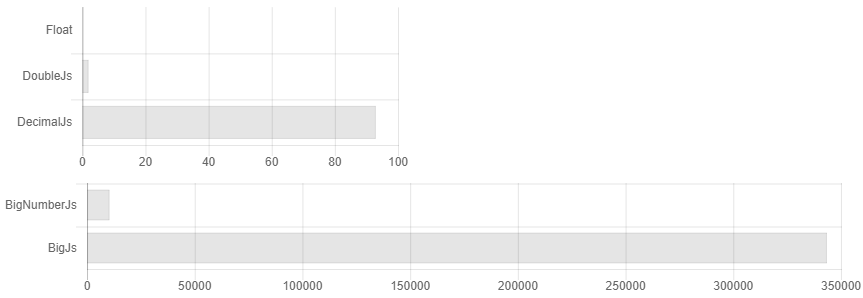
यही है, आपने 32 दशमलव स्थानों पर सटीकता सेट की है और ... उफ़, आपके पास पहले से 64 अंक हैं, 128. हम बहुत सटीक सोचते हैं! 256, 512 ... लेकिन मैंने 32 सेट किया! .. 1024, 2048 ... ऐसा कुछ 3,500 बार ओवरहेड दिखाई देता है। प्रलेखन में कहा गया है कि यदि आपके पास वैज्ञानिक गणना है, तो शायद दशमलव.जे आपके लिए बेहतर है। हालांकि वास्तव में, यदि आप समय-समय पर वैज्ञानिक गणना के लिए चक्कर लगाते हैं, तो Bignumber.js थोड़ा तेज़ काम करता है (चित्र 1 देखें)। यदि उन्हें परिवर्तन में नहीं दिया जा सकता है, तो उन्हें एक पैसे के सौवें हिस्से को कौन गिनना चाहिए? क्या कोई मामला है जब मुझे अधिक संकेतित संख्याओं को संग्रहीत करने की आवश्यकता है और कुछ अतिरिक्त वर्णों के साथ बाहर नहीं निकल सकते हैं? ऐसे दैत्य संख्या की सीमा को कैसे लेते हैं, जब कोई मनमानी संख्या के लिए टेलर श्रृंखला के अभिसरण की सख्त सटीकता को नहीं जानता है? सामान्य तौर पर, इस बात पर निराधार संदेह नहीं है कि स्कोन्हागे-स्ट्रैसेन गुणन एल्गोरिदम का उपयोग करके और उदाहरण के लिए, कॉर्डिक गणना के साथ साइन को खोजने के लिए, वहां गणना की गति को बढ़ाना संभव है।

Double.js

मैं निश्चित रूप से कहना चाहूंगा कि Double.js जल्दी और सही मायने रखता है। लेकिन यह पूरी तरह से सच नहीं है, अर्थात यह 10 गुना तेज है जिसे वह मानता है, लेकिन यह हमेशा सटीक नहीं होता है। उदाहरण के लिए, 0.3-0.1 यह प्रक्रिया कर सकता है, दोहरे भंडारण में और इसके विपरीत। लेकिन पाई नंबर को लगभग 32 अंकों की दोहरी सटीकता के साथ हल किया जा सकता है और यह वापस काम नहीं करता है। 16 वीं पर एक त्रुटि उत्पन्न होती है, जैसे कि एक अतिप्रवाह हो रहा है। सामान्य तौर पर, मैं js समुदाय से आग्रह करता हूं कि मैं एक साथ काम करने की कोशिश करूं, क्योंकि मैं फंस गया हूं। मैंने डिजिटल रूप से पार्स करने और डबल परिशुद्धता में विभाजित करने की कोशिश की, जैसे कि क्यूडी में, 16 अंकों के बैचों में विभाजित करते हैं और डबल परिशुद्धता में विभाजित करते हैं, बिग जेज का उपयोग करते हुए बिग जेज का उपयोग करते हुए मंटिसा को विभाजित करते हैं। अब मैं .parseFloat () में एक बग पर पाप करता हूं, क्योंकि निकटतम पूर्णांक के लिए आईईईई मानकों को ECMAScript 1 के साथ भी समर्थन किया जाता है। हालांकि आप निश्चित रूप से बाइनरी बफर को बांधने और प्रत्येक 0 और 1. का निरीक्षण करने की कोशिश कर सकते हैं, अगर आप इस समस्या को हल कर सकते हैं, तो तब bignumber.js से x10-x20 में त्वरण के साथ मनमानी सटीकता के साथ गणना करना संभव होगा। हालांकि, कई मैंडलब्रॉट यह पहले से ही गुणवत्ता प्रदान करता है, और आप इसे ज्यामितीय कार्यों के लिए उपयोग कर सकते हैं।

एक साल बाद, मैं यहां लौट आया और अभी भी पार्सिंग की समस्या को ठीक किया। समस्या केवल अपर्याप्त सटीकता में थी, जब 10 ^ (- n) से गुणा किया जाता था। सभी एल्गोरिदम को खरोंच से संशोधित किया गया है, और अब भयावह सटीकता और गति के साथ चलता है।



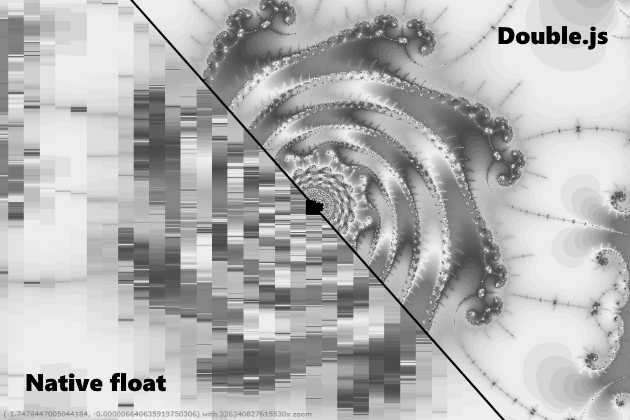
यहां लिबर के लिए एक लिंक है, एक इंटरैक्टिव बेंचमार्क और एक सैंडबॉक्स है जहां आप इसके साथ खेल सकते हैं।

सूत्रों का उपयोग किया

1. ओ। मोलर। फ्लोटिंग-पॉइंट अंकगणित में अर्ध दोहरी सटीकता। , 1965।
2. थियोडोरस डेकर। उपलब्ध सटीकता के विस्तार के लिए एक फ्लोटिंग-पॉइंट तकनीक , 1971. [ दर्शक ]
3. Mioara Joldes, Jean-Michel Muller, Valentina Popescu। डबल-शब्द अंकगणित , 2017 के बुनियादी भवन ब्लॉकों के लिए तंग और कठोर त्रुटि सीमा । [ PDF ]
4. मुलर, जे- एम। ब्रिसबार, एन। डे डाइनचिन, आदि। हैंडबुक ऑफ़ फ्लोटिंग-पॉइंट अंकगणित, अध्याय 14, 2010।
5. जोनाथन शेवचुक रोबॉट अडैप्टिव फ्लोटिंग-पॉइंट जियोमेट्रिक प्रेडिकेट्स , 1964। [ PDF ]
6. योज़ो हिदा, शियाओई ली, डेविड बेली। लाइब्रेरी डबल-डबल और क्वाड-डबल अंकगणित , 2000 के लिए। [ PDF ]